👔 🖱️ 🌉 Programação dinâmica em problemas de olimpíadas 🥁 ✌🏽 😖

Oi

Recentemente, resolvi problemas do arquivo Timus Online Judge e me deparei com uma seção chamada tarefas de programação dinâmica . Esse tipo de tarefa é de particular interesse para mim, porque muitas vezes essa abordagem garante a velocidade e a elegância da solução. O que é programação dinâmica?

A programação dinâmica é uma abordagem para resolver problemas em que há uma divisão em subtarefas que são "mais simples" em comparação com a original. A palavra "dinâmico" tem significado próximo de "indutivo": pressupõe-se que a resposta seja conhecida por algum significado

k

$k$ e quero encontrar a resposta para

k + 1

$k + 1$ . Em matemática, isso é chamado de transição indutiva e é a principal idéia da programação dinâmica.

Exemplos simples

A tarefa mais marcante e indicativa é a tarefa de calcular

n

$n$ número da sequência de Fibonacci. Sabe-se que a sequência possui as seguintes propriedades:

F_{0} = F_{1} = 1, F_{n} = F_{n - 1} + F_{n - 2} .

$F_0 = F_1 = 1, \ F_n = F_ {n-1} + F_ {n-2}.$

Isso implica imediatamente a fórmula de recorrência:

int Fibonacci(int n) { if(n == 1 || n == 2) return 1; return Fibonacci(n-1) + Fibonacci(n-2); }

Se a recursão estiver procurando por um número "do final", o método a seguir calcula sequencialmente todos os números localizados entre

0

$0$ e

n

$n$ :

 int dpFibonacci(int n) { int prev1 = 1; int prev2 = 1; int curr = 0; for(int j = 2; j < n; j++) { curr = prev1 + prev2; prev1 = prev2; prev2 = curr; } return curr; }

É claro que para empresas suficientemente grandes

n

$n$ esse algoritmo funciona muito mais rápido: ele não calcula valores intermediários várias vezes. Considere um exemplo um pouco mais complexo.

Exemplo 1. Você está andando em uma escada de pedágio. Para pisar

i

$i$ passo que você tem que pagar

a_{i}

$a_i$ moedas. Você pode passar para o próximo passo ou pular um. Tarefa: passar

n

$n$ passos e gaste o mínimo de moedas possível.

É claro que, percorrendo cada etapa, minimizamos o número de "pagamentos", mas podemos executar uma etapa muito cara, que gostaríamos de evitar. Crie uma matriz de valores

d

$d$ em que

j

$j$ o quinto lugar será o número (mínimo) de moedas que devem ser gastas para chegar a

j

$j$ ª etapa. É imediatamente claro que

d_{1} = a_{1}, d_{2} = a_{2}

$d_1 = a_1, \ d_2 = a_2$ . E então tomaremos no mínimo as duas etapas anteriores e adicionaremos o custo da própria etapa:

d_{i} = m i n l e f t (d_{i - 1}, d_{i - 2} r i g h t) + a_{i} .

$d_i = \ min \ left (d_ {i-1}, d_ {i-2} \ right) + a_ {i}.$

Mudamos um pouco as condições do problema: suponha que em algumas etapas você possa obter moedas (isso significa que

a_{k} < 0

$a_k <0$ ) O que precisa ser alterado no algoritmo para que ele dê o resultado correto?

Solução

Só é necessário mudar o "começo" de nossa dinâmica. Se a primeira escada não nos trouxer moedas, é aconselhável pular sobre ela, no entanto, se

a_{1} < 0

$a_1 <0$ , é melhor avançar e coletar suas moedas. Então

d_{2} = m i n e s q u e r d a (0, d_{1} d i r e i t a) + a_{2}

$d_2 = \ min \ esquerda (0, d_1 \ direita) + a_2$ .

Considere outro exemplo que usa dinâmica "bidimensional".

Exemplo 2. No labirinto há

n v e z e s m

$n \ vezes m$ quartos, cada um dos quais contém ouro (em uma gaiola

(i, j)

$(i, j)$ mentiras

a_{i j}

$a_ {ij}$ ouro). A tarefa é determinar qual quantidade máxima de ouro pode ser coletada com uma rota ideal a partir de um ponto

(0, 0)

$(0,0)$ direto ao ponto

(n, m)

$(n, m)$ se você pode ir para baixo ou para a direita.

Então, queremos saber a melhor rota para a célula

(i, j)

$(i, j)$ . Podemos chegar aqui de duas células -

(i - 1, j)

$(i-1, j)$ e

(i, j - 1)

$(i, j-1)$ . Dado que as rotas ideais para essas duas células são conhecidas (elas são armazenadas em alguma tabela

d

$d$ ), então a resposta para a célula

(i, j)

$(i, j)$ obtido da seguinte forma:

d_{i j} = m a x l e f t (d_{i - 1 j}, d_{i j - 1} r i g h t) + a_{i j} .

$d_ {ij} = \ max \ left (d_ {i-1j}, d_ {ij-1} \ right) + a_ {ij}.$

Essa é outra tarefa clássica de programação dinâmica, cujas modificações são bastante comuns em tarefas de programação esportiva. Uma tarefa semelhante é explicada em mais detalhes aqui .

Tarefas mais desafiadoras

Se desejado, uma abordagem dinâmica pode ser parafusada onde você quiser. Considere uma tarefa do arquivo Timus Online Judge.

A formulação matemática do problema é a seguinte: é necessário encontrar o número mínimo de termos necessários para decompor um determinado número em quadrados completos.

Como antes, suponha que sabemos as respostas para todos os números

k - 1

$k-1$ que são armazenados em alguma matriz

d

$d$ e gostaríamos de encontrar

d_{k}

$d_ {k}$ .

Pegue esse número

k

$k$ e analise quais situações podem ser:

$k$ é um quadrado cheio. Neste caso $d_ {k} = 1$ .
Talvez o número anterior $k-1$ era um quadrado completo. Então $d_ {k} = d_ {k-1} + 1$ .

Em geral, a opção de adicionar uma unidade à anterior não parece tão ruim.

Procuramos da seguinte forma: buscamos uma decomposição

k = q^{2} + s

$k = q ^ 2 + s$ tal que

d_{q^{2}} + d_{s} < d_{k - 1} + 1.

$d_ {q ^ 2} + d_s <d_ {k-1} + 1.$

Desde

q^{2}

$q ^ 2$ - quadrado cheio então

d_{q^{2}} = 1

$d_ {q ^ 2} = 1$ e

d_{s} < d_{k - 1},

$d_s <d_ {k-1},$

ou seja, encontramos uma partição simplesmente melhor do que

d_{k - 1} + 1

$d_ {k-1} + 1$ , e a resposta neste caso será

d_{k} = d_{s} + d_{q^{2}} = d_{s} + 1.

$d_k = d_ {s} + d_ {q ^ 2} = d_s + 1.$

Exemplo de código Java que implementa esse algoritmo:

 for(int k = 1; k <= n; k++) { int best = d[k - 1] + 1; //      int q = 1; while(k - q*q >= 0) { // k = q*q + s if(k - q*q == 0) { // k -   best = 1; break; } else if(d[k - q*q] < best) best = d[k - q*q] + 1; q++; } d[k] = best; }

Considere o seguinte problema . O objetivo é construir uma escada de

N

$N$ cubos de acordo com as regras:

a escada tem pelo menos dois degraus;
uma escada não pode ter dois degraus idênticos;
os degraus da escada estão em ordem crescente (ou seja, o próximo é maior que o anterior).

Desta vez, construiremos uma dinâmica bidimensional. Crie uma tabela

d

$d$ em que a posição

(i, j)

$(i, j)$ o número de escadas constituídas por

i

$i$ cubos cuja altura não exceda

j

$j$ . Se der certo, a resposta para o nosso problema será a soma

s u m l i m i t s_{j = 1}^{n} d_{n j} .

$\ sum \ limits_ {j = 1} ^ n d_ {nj}.$

Então, resolveremos o problema de encontrar o número de escadas compostas por

i

$i$ cubos que são altos

j

$j$ . A imagem mostra as escadas que caem

d_{74}

$d_ {74}$ :

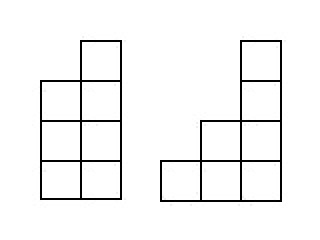
Como conhecemos todas as escadas, que consistem em menos cubos, "separaremos" as escadas

(i, j)

$(i, j)$ coluna da direita. O resultado é uma escada c

i - j

$i-j$ cubos. Exemplo para

i = 9, j = 4

$i = 9, \ j = 4$ :

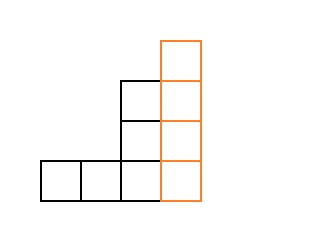
Mas para essas escadas, o resultado já é conhecido, portanto, classificaremos todas essas escadas com um ciclo em

k

$k$ e adicione todos os resultados. Desta maneira

d_{i j} = s o m a l i m i t e s_{k = 1}^{j - 1} d_{i - j k} .

$d_ {ij} = \ soma \ limites_ {k = 1} ^ {j-1} d_ {i-jk}.$

Agora vamos classificar as alturas das escadas:

d_{i j} = s o m a l i m i t e s_{k = 1}^{j - 1} d_{i - j k}, j = o v e r l i n e 1, i .

$d_ {ij} = \ soma \ limites_ {k = 1} ^ {j-1} d_ {i-jk}, \ j = \ overline {1, i}.$

Finalmente, mudar

i

$i$ de

1

$1$ antes

n

$n$ nós obtemos a resposta.

Importante : no processo de construção de nossa matriz, é necessário levar em consideração

d_{i i} = 1

$d_ {ii} = 1$ , pois, caso contrário, alguns tipos de escadas serão "perdidos" (quando "separados"), mas não é preciso dizer que essa escada não satisfaz as condições do problema; portanto, a resposta será o número

d_{n n} - 1

$d_ {nn} - 1$ .

Exemplo de código Java que implementa esse algoritmo:

 dp = new long[n + 1][n+1]; d[1][1] = 1; d[2][1] = 0; d[2][2] = 1; for(int i = 3; i < n + 1; i++) { for(int j = 2; j <i; j++) { long cnt = 0; for(int k = 1; k < j; k++) { cnt += d[i - j][k]; } d[i][j] = cnt; } d[i][i] = 1; //    } long answer = 0L; for(int i = 0; i <= n; i++) { answer += d[n][i]; } answer--; //

A próxima tarefa é resolvida usando uma matriz unidimensional.

Então, o que temos. O primeiro ent sabe 2 palavras. Cada um ensina todas as palavras que ele conhece a si próprio dois: jovens e velhos. Por sua vez, os jovens foram ensinados com tantas palavras quanto ele já sabia, e os velhos foram ensinados apenas uma palavra. Você precisa saber quantos Ents sabem exatamente

K

$K$ palavras (é necessário deduzir o número desses módulos ents

P

$P$ )

A solução é bastante simples. Crie uma matriz

d

$d$ em que

i

$i$ -th lugar vamos armazenar o número de ents (módulo

P

$P$ ) quem sabe

i

$i$ palavras. Tudo começa com o primeiro ent, que conhece duas palavras, portanto

d_{2} = 1

$d_2 = 1$ . E então tudo é simples:

Todas as entradas que conhecem um número ímpar de palavras são antigas e só podem aprender com as anteriores. Portanto, para ímpares $i: \ d_i = d_ {i-1};$
Quanto aos ents que conhecem um número par de palavras, são todos aqueles que receberam a mesma quantidade de palavras dos elfos (jovens) $+$ aqueles que aprenderam com o anterior (antigo); isto é, mesmo $i$ nós temos $d_i = d _ {{i \ barra invertida 2}} + d_ {i-1}$ .

Resta lidar com o módulo de cálculo. Para não armazenar grandes números, lembraremos imediatamente de todos os valores do módulo.

Exemplo de código Java que implementa esse algoritmo:

 int[] d = new int[K + 1]; if(K >= 2) d[2] = 1; if(P != 1) { for(int i = 3; i <= K; i++) { if(i % 2 != 0) { d[i] = d[i - 1]; } else { d[i] = ((d[i/2] % P) + d[i - 1] % P) % P; } } } else d[K] = 0;

Recursos utilizados:

Timus Online Judge;
Um pouco sobre programação dinâmica;
Módulo de propriedades de comparação.

Programação dinâmica em problemas de olimpíadas

Exemplos simples

Tarefas mais desafiadoras

More articles: