1. Introdução
A equação do tipo elíptico mais comum é a equação de Poisson.
Muitos problemas de física matemática são reduzidos à solução dessa equação, por exemplo, os problemas da distribuição estacionária de temperatura em um sólido, problemas de difusão, os problemas da distribuição do campo eletrostático em um meio não condutor na presença de cargas elétricas e muitos outros.
Para resolver equações elípticas no caso de várias medições, métodos numéricos são usados para converter equações diferenciais ou seus sistemas em sistemas de equações algébricas. A precisão da solução é determinada pela etapa da grade de coordenadas, o número de iterações e a grade de bits do computador [1]
O objetivo da publicação é obter uma solução para a equação de Poisson para as condições de contorno de Dirichlet e Neumann, para investigar a convergência do método de relaxamento da solução usando exemplos.
A equação de Poisson refere-se a equações do tipo elíptico e, no caso unidimensional, tem a forma [1]:
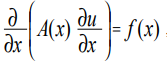
(1)
onde x é a coordenada; u (x) é a função desejada; A (x), f (x) são algumas funções de coordenadas contínuas.
Resolvemos a equação unidimensional de Poisson para o caso A = 1, que neste caso assume a forma:

2)
No intervalo [xmin, xmax], definimos uma grade de coordenadas uniforme com um passo Δ:
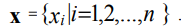
(3)
As condições de contorno do primeiro tipo (condições de Dirichlet) para o problema em consideração podem ser representadas como:

4)
onde x1, xn são as coordenadas dos pontos de contorno da região [xmin, xmax]; g1, g2 - alguns
constantes.
As condições de contorno do segundo tipo (condições de Neumann) para o problema em consideração podem ser representadas como:

(5)
Discretizando as condições de contorno de Dirichlet em uma grade de coordenadas uniforme (3) usando o método das diferenças finitas, obtemos:
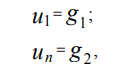
(6)
onde u1, un são os valores da função u (x) nos pontos x1, xn, respectivamente.
Discretizando as condições de contorno de Neumann na grade (3), obtemos:

(7)
Discretizando a equação (2) para pontos de grade internos, obtemos:
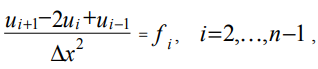
(8)
onde ui, fi são os valores das funções u (x), f (x) no ponto da grade com a coordenada xi.
Assim, como resultado da discretização, obtemos um sistema de equações algébricas lineares da dimensão n contendo n - 2 equações da forma (8) para pontos internos da região e equações (6) e (7) para dois pontos de contorno [1].
A seguir, é apresentada uma lista em Python de uma solução numérica para a equação (2) com condições de contorno (4) - (5) na grade (3).
Solução de Listagemfrom numpy import* from numpy.linalg import solve import matplotlib.pyplot as plt x0=0
Temos:


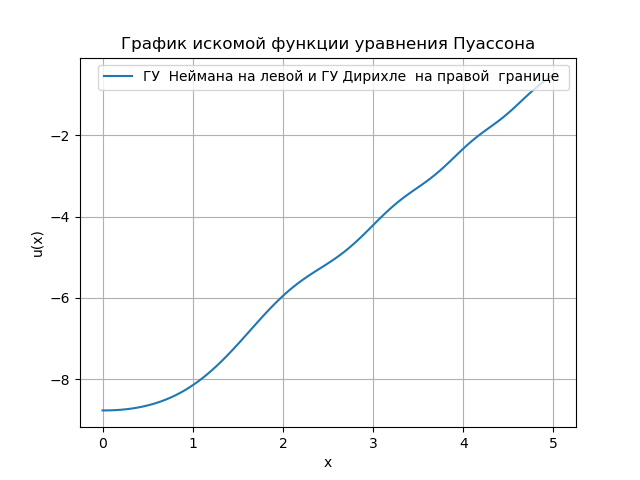

O programa que desenvolvi em Python é conveniente para analisar condições de contorno.O algoritmo de solução Python acima usa a função Numpy - u = linalg.solve (a, bT) .T para resolver um sistema de equações algébricas, o que aumenta a velocidade com a matriz quadrada {a}. No entanto, com um aumento no número de medições, é necessário mudar para o uso de três matrizes diagonais, cuja solução é complicada mesmo para uma tarefa muito simples, encontrei um exemplo no fórum:
Exemplo de solução com matriz três diagonal from __future__ import print_function from __future__ import division import numpy as np import time ti = time.clock() m = 1000 A = np.zeros((m, m)) B = np.zeros((m, 1)) A[0, 0] = 1 A[0, 1] = 2 B[0, 0] = 1 for i in range(1, m-1): A[i, i-1] = 7 A[i, i] = 8 A[i, i+1] = 9 B[i, 0] = 2 A[m-1, m-2] = 3 A[m-1, m-1] = 4 B[m-1, 0] = 3 print('A \n', A) print('B \n', B) x = np.linalg.solve(A, B)
O programa de solução numérica do uniforme em cada direção do problema de Dirichlet da grade para a equação de convecção-difusão
[2]

(9)
Utilizamos aproximações por diferenças centrais para o termo convectivo e um método de relaxamento iterativo.Para a dependência da taxa de convergência no parâmetro relaxamento para a solução numérica do problema com f (x) = 1 e 6 (x) = 0,10. Na tarefa de grade:

(10)
Representamos a matriz A como a soma das matrizes diagonal, triangular inferior e triangular superior:

(10)
O método de relaxamento corresponde ao uso do método iterativo :
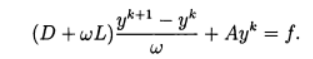
(11)
At

\ falar sobre relaxamento superior, quando
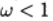
- sobre relaxamento menor.
Listagem de Programas from numpy import * """ - . .""" def relaxation(b, f, I1, I2, n1, n2, omega, tol = 1.e-8): h1 = I1 / n1 h2 = I2 / n2 d = 2. / h1**2 + 2. / h2**2 y = zeros([n1+1, n2+1]) ff = zeros([n1+1, n2+1]) bb = zeros([n1+1, n2+1]) for j in arange(1,n2,1): for i in arange(1,n1,1): ff [i,j] = f(i*h1, j*h2) bb[i,j] = b(i*h1, j*h2)
)
Temos:
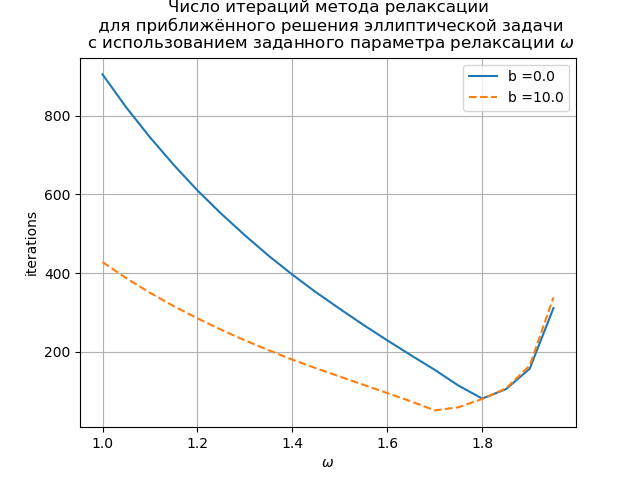
O gráfico mostra a dependência do número de iterações no parâmetro de relaxamento para a equação de Poisson (b (x) = 0) e a equação de convecção-difusão (b (x) = 10). Para a equação da grade de Poisson, o valor ótimo do parâmetro de relaxamento é encontrado analiticamente, e o método iterativo converge em

.
Conclusões:
- A solução do problema elíptico em Python com um sistema flexível para definir condições de contorno
- Demonstra-se que o método de relaxamento possui uma faixa ideal (
 ) parâmetro de relaxamento.
) parâmetro de relaxamento.
Referências:
- Ryndin E.A. Métodos para resolver problemas de física matemática. - Taganrog:
Editora da TRTU, 2003. - 120 p. - Vabishchevich P.N. Métodos Numéricos: Workshop Computacional. - M .: Livraria
Librocom, 2010. - 320 p.