🍴 👨🏻‍🎨 ↩️ Modelagem da superfície da água usando o processador FFT e NeuroMatrix DSP 🎁 😀 👿

A bem conhecida transformação rápida de Fourier tem sido usada não apenas para solucionar problemas de processamento de sinal digital, reconhecimento de objetos na imagem, mas também em computação gráfica. Jerry Tessendorf descreveu um modelo matemático que permite sintetizar as ondas do oceano e animá-las em tempo real. Este modelo é baseado em uma FFT bidimensional.

Quando fui incumbido de desenvolver um aplicativo para um processador DSP que visualiza a operação de uma FFT, percebi que a modelagem de ondas é perfeita para essa finalidade.

Modelo matemático da onda

A idéia básica de um modelo matemático de uma onda pode ser descrita pela expressão:

m a t h b f H

$\ mathbf H$ = FFT2D (

m a t h b f w i d e t i l d e H

$\ mathbf {\ widetilde H}$ ), FFT2D é indicado como o operador de uma FFT bidimensional.

m a t h b f H

$\ mathbf H$ É o campo de altura da superfície da água (tamanho da matriz

n_{1} x n_{2}

$n_1 x n_2$ onde

n_{1}

$n_1$ e

n_{2}

$n_2$ pode assumir valores de potências de dois). Os elementos dessa matriz são as alturas das ondas.

m a t h b f w i d e t i l d e H

$\ mathbf {\ widetilde H}$ - sinal (tamanho da matriz

n_{1} x n_{2}

$n_1 x n_2$ ), gerado de acordo com uma determinada lei e dependendo do tempo.

m a t h b f w i d e t i l d e H = m a t h b f w i d e t i l d e H_{0} . * m a t h b f A + o v e r l i n e m a t h b f w i d e t i l d e H_{0} . * o v e r l i n e m a t h b f A

$\ mathbf {\ widetilde H} = \ mathbf {\ widetilde H_0}. * \ mathbf A + \ overline {\ mathbf {\ widetilde H_0}}. * \ overline {\ mathbf A}$ onde os elementos da matriz

m a t h b f A

$\ mathbf A$ é

$ inline $ e ^ {iω_ {ij} t} = cos⁡ (ω_ {ij} t) + isin (ω_ {ij} t) $ inline $ e a matriz

o v e r l i n e m a t h b f A

$\ overline {\ mathbf A}$ - conjugado complexo a

m a t h b f A

$\ mathbf A$ matriz

i = 0, 1, . . . n_{1}, j = 0, 1, . . . n_{2}

$i = 0,1, ... n_1, j = 0,1, ... n_2$

ω_{i j}

$ω_ {ij}$ São elementos da matriz

L a r g e m a t h b f ω

$\ Large {\ mathbf ω}$ .

. *

$. *$ - multiplicação de matrizes elementares.

m a t h b f w i d e t i l d e H_{0}

$\ mathbf {\ widetilde H_0}$ - campo de alturas no momento inicial t = 0.

o v e r l i n e m a t h b f w i d e t i l d e H_{0}

$\ overline {\ mathbf {\ widetilde H_0}}$ - conjugado complexo a

m a t h b f w i d e t i l d e H_{0}

$\ mathbf {\ widetilde H_0}$ matriz (tamanho

n_{1} x n_{2}

$n_1 x n_2$ )

Para criar uma animação do movimento das ondas em tempo real, é necessário recontar a matriz

m a t h b f w i d e t i l d e H

$\ mathbf {\ widetilde H}$ e

m a t h b f H

$\ mathbf H$ mudando t . Matrizes

m a t h b f w i d e t i l d e H_{0}

$\ mathbf {\ widetilde H_0}$ ,

o v e r l i n e m a t h b f w i d e t i l d e H_{0}

$\ overline {\ mathbf {\ widetilde H_0}}$ e

L a r g e m a t h b f ω

$\ Large {\ mathbf ω}$ são calculados uma vez e reutilizados.

Agora, vamos à descrição do processador DSP, que, com base nas fórmulas acima, precisa ser capaz de:

Calcular FFT.
Multiplique matrizes elemento por elemento.
Adicione matrizes.
Calcule o vetor de senos e cossenos.

Como processador DSP, o 1879VM6Ya foi usado com base na arquitetura NeuroMatrix, desenvolvida pelo Centro Científico e Técnico "Módulo" CJSC. O circuito na Figura 1.

O processador contém 2 núcleos operacionais paralelos NMPU0 e NMPU1 (operando com uma frequência de 500 MHz), cada um com um processador RISC e um coprocessador vetorial (NMCore FPU para ponto flutuante e NMCore INT para aritmética inteira). O núcleo NMPU0 é para processamento de dados de ponto flutuante e NMPU1 é para dados inteiros. O NMPU0 possui 8 bancos de SRAM interna (128 kB cada) e o NMPU1 possui 4 bancos (128 kB) da mesma memória. Em 1879VM6Ya, um controlador DMA e uma interface DDR2 estão instalados.

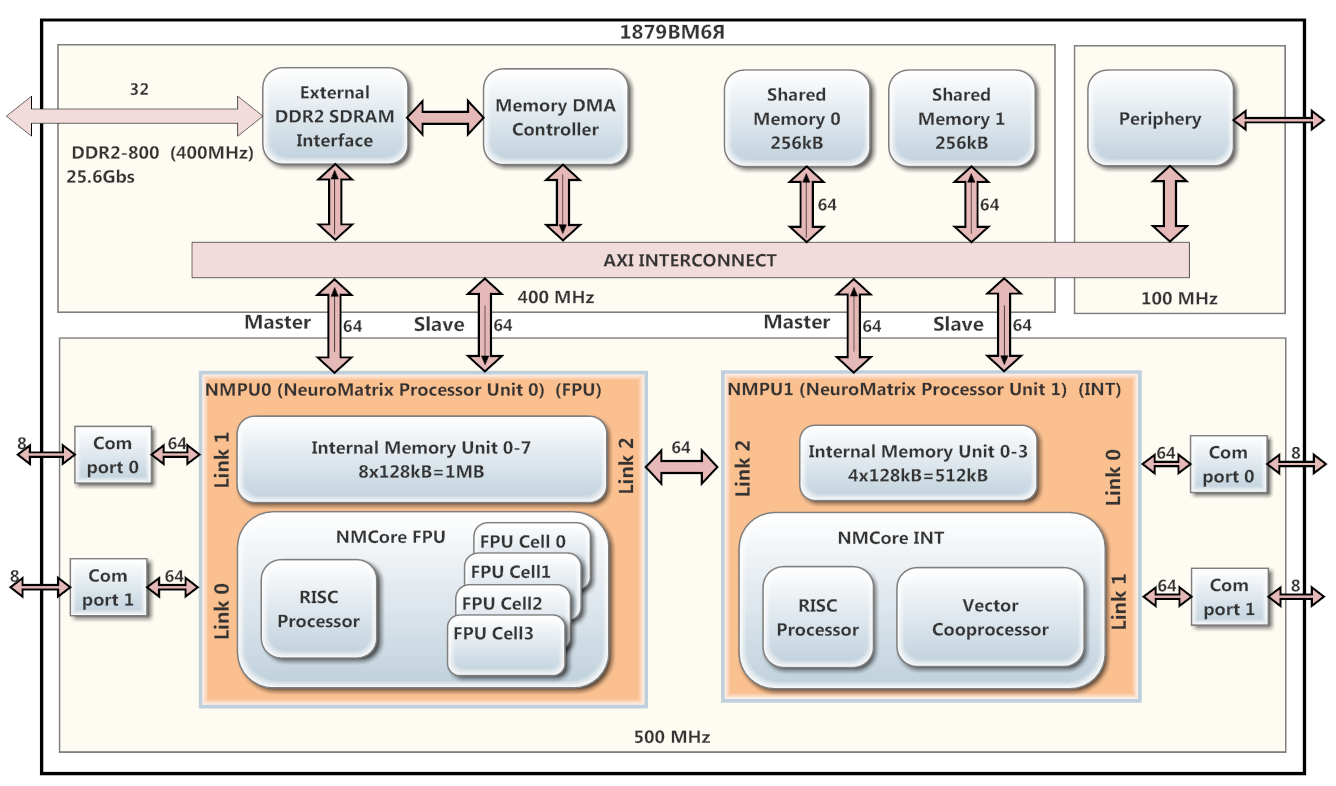imagem

Fig. 1. Diagrama do processador 1879VM6YA

O processador está localizado no módulo de instrumento MC121.01 (consulte a Fig. 2). Este módulo também possui 512 MB de memória DDR2.

imagem

Fig. 2. MS121.01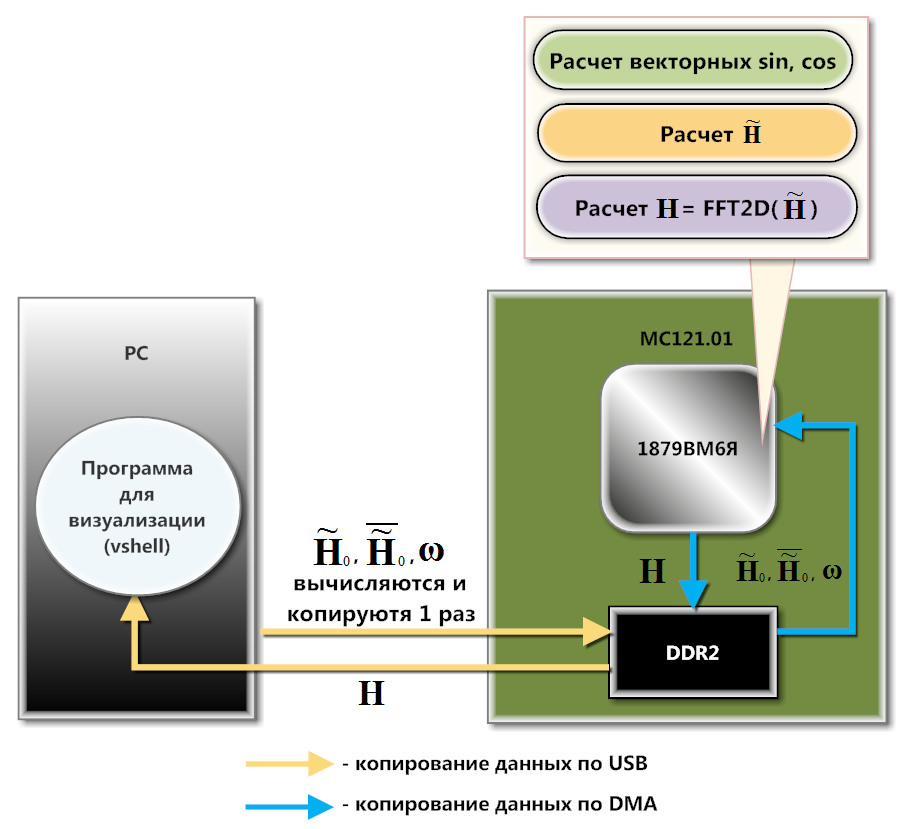

Fig. 3. Esquema de interação de MC121.01 e PC

O MC121.01 interage com o PC via USB (diagrama na Figura 3). No nível do software, essa interação é organizada usando a biblioteca de download e troca de dados, que faz parte do SDK desta placa. Matrizes pré-computadas

m a t h b f w i d e t i l d e H_{0}

$\ mathbf {\ widetilde H_0}$ ,

o v e r l i n e m a t h b f w i d e t i l d e H_{0}

$\ overline {\ mathbf {\ widetilde H_0}}$ e

L a r g e m a t h b f ω

$\ Large {\ mathbf ω}$ são carregados na memória DDR2 através das funções da biblioteca de downloads e trocas. Cópias do controlador DMA

m a t h b f w i d e t i l d e H_{0}

$\ mathbf {\ widetilde H_0}$ ,

o v e r l i n e m a t h b f w i d e t i l d e H_{0}

$\ overline {\ mathbf {\ widetilde H_0}}$ e

L a r g e m a t h b f ω

$\ Large {\ mathbf ω}$ linha por linha na memória interna (SRAM) do processador. O download para DDR2 se deve ao fato de nenhuma dessas matrizes se encaixar completamente na SRAM. A cópia linha a linha ocorre aqui, porque o 1879BM6Ya calcula a partir da SRAM mais rapidamente que a partir da DDR2. Além disso, uma parte significativa dos cálculos pode ser feita no contexto da DMA.

Usando as funções de vetor da biblioteca NMPP para calcular senos, cossenos, multiplicação e adição de vetores, o processador calcula as linhas da matriz

m a t h b f w i d e t i l d e H

$\ mathbf {\ widetilde H}$ e tira a FFT unidimensional deles. O resultado é enviado pelo DMA de volta ao DDR2. Assim, no DDR2 é formada uma matriz intermediária, a partir das colunas nas quais o processador calcula a FFT unidimensional (após carregar as colunas da matriz intermediária pelo DMA no SRAM). Assim, uma matriz é formada em DDR2

m a t h b f H

$\ mathbf H$ . Essa matriz é baixada no PC para desenhar um único quadro com a imagem da superfície da onda. Para animar a imagem em tempo real, é necessário calcular a matriz de acordo com o algoritmo descrito acima

m a t h b f H

$\ mathbf H$ aumentando o parâmetro t .

Na prática, verifica-se que 18796 calcula a matriz

m a t h b f H

$\ mathbf H$ mais rápido que o PC o esvazia. Por esse motivo, o processador pode estar ocioso, aguardando o PC pegar o próximo lote de dados. Foi possível resolver esse problema usando um buffer de anel (contendo várias matrizes

m a t h b f H

$\ mathbf H$ ) organizado na placa de memória DDR2.

No nível do software, o trabalho com o controlador DMA e o buffer de anel são executados usando as funções da biblioteca HAL (Hardware abstraction Level) para processadores NeuroMatrix.

Visualização da superfície das ondas

Quando o DEM

m a t h b f H

$\ mathbf H$ carregado na memória do PC, você pode visualizar a superfície. Para exibi-lo mais claramente, você precisa coordenar x, y, z, descrevendo os pontos na superfície, multiplicados pela matriz de rotação . Então, obtemos as novas coordenadas da superfície x ', y', z ', girando-a em um determinado ângulo.

Ao escalar as novas coordenadas e conectar os pontos ao longo deles com linhas retas, você pode ver a animação das ondas do oceano (veja o vídeo abaixo). Para visualização da superfície, a biblioteca usada para exibir a imagem na tela vshell.

Conclusão

Concluindo, quero dizer que o cálculo e transmissão via USB de uma matriz

m a t h b f H

$\ mathbf H$ com um tamanho de 256x256 números flutuantes, são gastos ~ 4,7 milhões de ciclos de clock (72 ciclos de clock por flutuador). A taxa de quadros é ~ 107. Se você não levar em consideração o tempo necessário para transferir dados via USB, os cálculos custarão ~ 2,5 milhões de ciclos (38 ciclos por flutuação). Este é o tempo total gasto pelo processador de 1879º6 na multiplicação por elementos e adição de matrizes, cálculo de FFT, senos, cossenos e cópia usando DMA. Esses cálculos são realizados no contexto da transferência de dados USB.

A diferença de 2,2 milhões de ciclos de clock (4,7 milhões - 2,5 milhões = 2,2 milhões) indica que no sistema PC-MC121.01 o USB é um "gargalo" e o 1879VM6YA pode ser carregado com cálculos em 46% a mais sem receber rebaixamento FPS.

Gostaria também de observar que, no contexto da transferência de dados USB e dos cálculos em um coprocessador para um ponto flutuante, um coprocessador para aritmética inteira, que não foi usado nesta tarefa, pode ser usado.

A tabela mostra o desempenho de algumas funções vetoriais da biblioteca nmpp.

Função	Bares
FFT unidimensional, 256 pontos	1770
Seno, 256 pontos	1400
Cosine, 256 pontos	1400

Referências:

NMPP - uma biblioteca de primitivos para a arquitetura NeuroMatrix
HAL - Biblioteca de abstração dependente de hardware do NeuroMatrix
VSHELL - biblioteca de processamento e exibição de imagens

Modelagem da superfície da água usando o processador FFT e NeuroMatrix DSP

Modelo matemático da onda

Visualização da superfície das ondas

Conclusão

Referências:

More articles: