Tarefas do livro escolar I

Parte I
Parte II
Parte III

Considere a solução algorítmica para o problema número 38 do livro "Tarefas para crianças de 5 a 15 anos"

Calcule a quantidade:

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}$$

(com um erro não superior a 1% da resposta)

Abaixo está um algoritmo para calcular somas parciais desta série no esquema (Lisp) no drRacket (o drRacket permite executar cálculos em frações comuns):

#lang racket (define series_sum ( lambda (n) (if (= n 0) 0 (+ (/ 1 (* n (+ n 1))) (series_sum(- n 1))) ) ) ) (series_sum 10) (series_sum 100) (series_sum 1000) (series_sum 10000) (series_sum 100000) (series_sum 1000000) (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* n (+ n 1.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 10) (series_sum_1 100) (series_sum_1 1000) (series_sum_1 10000) (series_sum_1 100000) (series_sum_1 1000000) 

Os últimos dois exemplos drRacket calculados com um erro



Este programa pode ser executado no ide ide.com.com online e codepad.org .



Se considerarmos somas parciais em frações comuns, podemos ver que a soma da série é

$$

$$\ frac {n} {n + 1}$$

Deixe-me lembrá-lo que $$$\ lim \ frac {n} {n + 1} = \ frac {1} {1+ \ frac {1} {n}} = \ frac {1} {1} = 1$ às $$$n \ a \ infty$

O segundo volume do Curso de Cálculo Diferencial e Integral 363 (4) considera o caso geral

$$

$$\ sum \ frac {1} {(\ alpha + n) (\ alpha + n +1)} = \ frac {1} {\ alpha + 1}$$

A tarefa do curso "Matemática para Desenvolvedores":
Encontre o número de membros em uma sequência $$$\ frac {2n-1} {4n + 5}$ deitado fora do intervalo $$$(1- \ frac {1} {1000}; 1+ \ frac {1} {1000})$

Vamos para o tópico principal do artigo.

Vamos considerar mais um exemplo de um livro de problemas.
43 Números de coelhos (Fibonacci), formam uma sequência $$$(a_ {1} = 1), 1, 3, 5, 8, 13, 21, 34, ...,$ em que $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ para todos $$$n = 1, 2, ...$ . Encontre o maior divisor comum de números $$$a_ {100}$ e $$$a_ {99}$ .

Resposta: Dois números Fibonacci adjacentes são coprime, ou seja, $$$\ gcd (u_ {n + 1}, u_ {n}) = 1$
(gcd é o maior divisor comum, ou seja, GCD).

“Prova do livro“ Além das páginas de um livro de matemática ”[10-11]


Na próxima tarefa, você precisa calcular a proporção áurea , $$$\ frac {\ sqrt {5} + 1} {2} \ aproximadamente 1.618$ . [Essa é a proporção de um cartão postal que permanece semelhante ao cortar um quadrado cujo lado é o lado menor do cartão postal.]

53 Para uma sequência de números de Fibonacci $$$a_ {n}$ tarefas 43 encontrar o limite do relacionamento $$$\ frac {a_ {n + 1}} {a_ {n}}$ enquanto se esforça $$$n$ até o infinito:

$$

$$\ frac {a_ {n + 1}} {a_ {n}} = 2, \ frac {3} {2}, \ frac {5} {3}, \ frac {8} {5}, \ frac { 13} {8}, \ frac {21} {13}, \ frac {34} {21}.$$

Considere os segmentos que representam as diferenças de dois membros adjacentes da série $$$\ frac {a_ {n + 1}} {a_ {n}}$ .

Mesmo os membros da série $$$\ frac {a_ {n + 1}} {a_ {n}}$ representam uma sequência crescente $$$x_ {n}$

$$

$$\ frac {3} {2}, \ frac {8} {5}, \ frac {21} {13}, ...,$$

Membros de linha ímpares $$$\ frac {a_ {n + 1}} {a_ {n}}$ representam uma sequência decrescente $$$y_ {n}$

$$

$$2, \ frac {5} {3}, \ frac {13} {8}, ...,$$

Pelo lema do intervalo incorporado (Curso de cálculo diferencial e integral, 38)

$$

$$c = \ lim x_ {n} = \ lim y_ {n}$$

Para a nossa linha em um ponto $$$c$ igualdade justa $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = \ frac {a_ {n + 1}} {a_ {n}}$

Dividindo $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ em $$$a_ {n + 1}$ nós obtemos a equação $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = 1 + \ frac {a_ {n}} {a_ {n + 1}}$ .
Substituindo $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = x, \ frac {a_ {n}} {a_ {n + 1}} = \ frac {1} {x}$ obtemos a equação quadrática $$$x = 1 + \ frac {1} {x}$ .

Se no programa geogebra conectamos os pontos 2 e $$$\ frac {3} {2}$ , $$$\ frac {3} {2}$ e $$$\ frac {5} {3}$ , $$$\ frac {5} {3}$ e $$$\ frac {8} {5}$ etc. - obter uma figura auto-semelhante




Em geral, existe um algoritmo padrão para calcular números de Fibonacci em Python.
Este algoritmo está disponível no Python.org

 def fib(n): a, b = 0, 1 while a < n: print(a) a, b = b, a+b fib(100) 

Você pode verificar o link
Altere esse algoritmo para que ele imprima uma aproximação à proporção áurea. Para dois números adjacentes aeb, dividiremos a soma a + b por b

 def fib(n): a, b = 0.0 , 1.0 while a < n: print((a+b)/b) a, b = b, a+b fib(100) 

Você pode verificar o link

Aqui estão algumas tarefas do tutorial do SICP relacionadas à proporção áurea.


O exemplo a seguir do livro de tarefas "Tarefas para crianças de 5 a 15 anos"
54 Calcular fração contínua infinita

$$

$$1 + \ frac {1} {2 + \ frac {1} {1+ \ frac {1} {2+ \ frac {1} {1+ \ frac {1} {2 + ...}}}}}$$

UPD Considere a equação

$$

$$\ alpha = 1+ \ frac {1} {2 + \ frac {1} {\ alpha}}$$

De acordo com os Teoremas 236 e 235 do livro "Teoria dos Números":

$$

$$\ alpha = \ frac {P_ {1} \ alpha + P_ {0}} {Q_ {1} \ alpha + Q_ {0}}$$

Nós compomos uma tabela de valores $$$P_ {n}$ e $$$Q_ {n}$ às $$$n = 0,1:$



para que $$$\ alpha = \ frac {3 \ alpha + 1} {2 \ alpha + 1}, 2 \ alpha ^ {2} - 2 \ alpha -1 = 0$

e desde $$$\ alpha> 0,$ então

$$

$$\ alpha = \ frac {1 + \ sqrt {3}} {2}$$

Considere o problema do livro “Atrás das páginas de um livro de matemática” [10-11]
4) Mostrar esse número $$$\ sqrt {1+ \ sqrt {1 + \ sqrt {1 + ...}}}$ igual ao número $$$\ varphi$ definindo a proporção áurea.

Considere a opção $$$x_ {n} = \ sqrt {c + \ sqrt {c + ... + \ sqrt {c}}}$
Curso de cálculo diferencial e integral, 35 (2)

Desta maneira $$$x_ {n + 1}$ obtido de $$$x_ {n}$ de acordo com a fórmula

$$

$$x_ {n + 1} = \ sqrt {c + x_ {n}}$$

... Pelo teorema principal, opções $$$x_ {n}$ tem algum limite finito $$$a$ . Para determiná-lo, passamos ao limite na igualdade

$$

$$x_ {n + 1} ^ {2} = c + x_ {n};$$

Ficamos de tal maneira que $$$a$ satisfaz a equação quadrática

$$

$$a ^ {2} = c + a$$

Esta equação tem as raízes de diferentes sinais; mas o limite que nos interessa $$$a$ não pode ser negativo; portanto, é igual exatamente à raiz positiva:

$$

$$a = \ frac {\ sqrt {4c + 1} + 1} {2}$$

A partir do qual podemos concluir que a "proporção áurea" é uma solução para a equação $$$a ^ {2} = c + a$
às $$$c = 1$ .


Além disso, no Curso de Cálculo Diferencial e Integral, 35 (3), um algoritmo para calcular o número inverso é considerado

Vamos $$$c$ É qualquer número positivo e coloca $$$x_ {n} = cy_ {n}$ . A relação de recursão escrita acima será substituída por:

$$

$$y_ {n + 1} = y_ {n} (2 - cy_ {n})$$

Tomando o valor inicial $$$y_ {0}$ sob a condição: $$$0 <y_ {0} <\ frac {1} {c}$ nós entendemos isso $$$y_ {n}$ monotonamente crescente, tenderá a $$$\ frac {1} {c}$ . De acordo com esse esquema, em máquinas de contagem, o número inverso é calculado $$$c$ .

Algoritmo de cálculo de número inverso $$$c$ em Python:
( Ideone.com e codepad.org )

 def reciprocal(c,y0,n): arr=[] for i in range(n): arr.append(y0) y0=y0*(2-c*y0) return arr 

A função recíproca recebe um número como entrada $$$c$ valor inicial $$$y_ {0}$ , número de iterações $$$n$ e retorna uma matriz de "aproximações" para o número $$$\ frac {1} {c}$ .
$$$y_ {0} = 0,1$ às $$$c <10$
$$$y_ {0} = 0,01$ às $$$10 <c <100$
$$$y_ {0} = 0,001$ às $$$100 <c <1000$
etc.
Exemplos de como a função recíproca funciona com vários $$$c$

 >>> reciprocal(3,0.1,10) 

[0,1, 0,17, 0,2533, 0,31411733000000003, 0,3322255689810133, 0,3333296519077525,
0,3333333332926746, 0,3333333333333333337, 0,3333333333333333337, 0,3333333333333333337]

 >>> reciprocal(8,0.1,10) 

[0,1, 0,12, 0,1248, 0,12499968, 0,1249999999991808, 0,125, 0,125, 0,125, 0,125, 0,125]

 >>> reciprocal(5,0.1,10) 

[0.1, 0.15000000000000002, 0.18750000000000003, 0.19921875000000003, 0.19999694824218753, 0.1999999999534339, 0.20000000000000004, 0.19999999999999998,
0.19999999999999998, 0.19999999999999998]

Interpretação geométrica

Vamos tentar usar o método tangente para aproximar o número inverso.
Tangentes $$$y = f '(x_ {0}) (x-x_ {0}) + f (x_ {0})$ para funcionar gráfico $$$y = \ frac {1} {x}$ são expressos pela fórmula $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}}$

Substituindo Números $$ em vez de $$$x_ {0}$ obtemos as equações das tangentes

$$

$$y = 2-x$$

$$

$$y = 1- \ frac {x} {4}$$

$$

$$y = \ frac {2} {3} - \ frac {x} {9}$$

$$

$$y = \ frac {1} {2} - \ frac {x} {16}$$

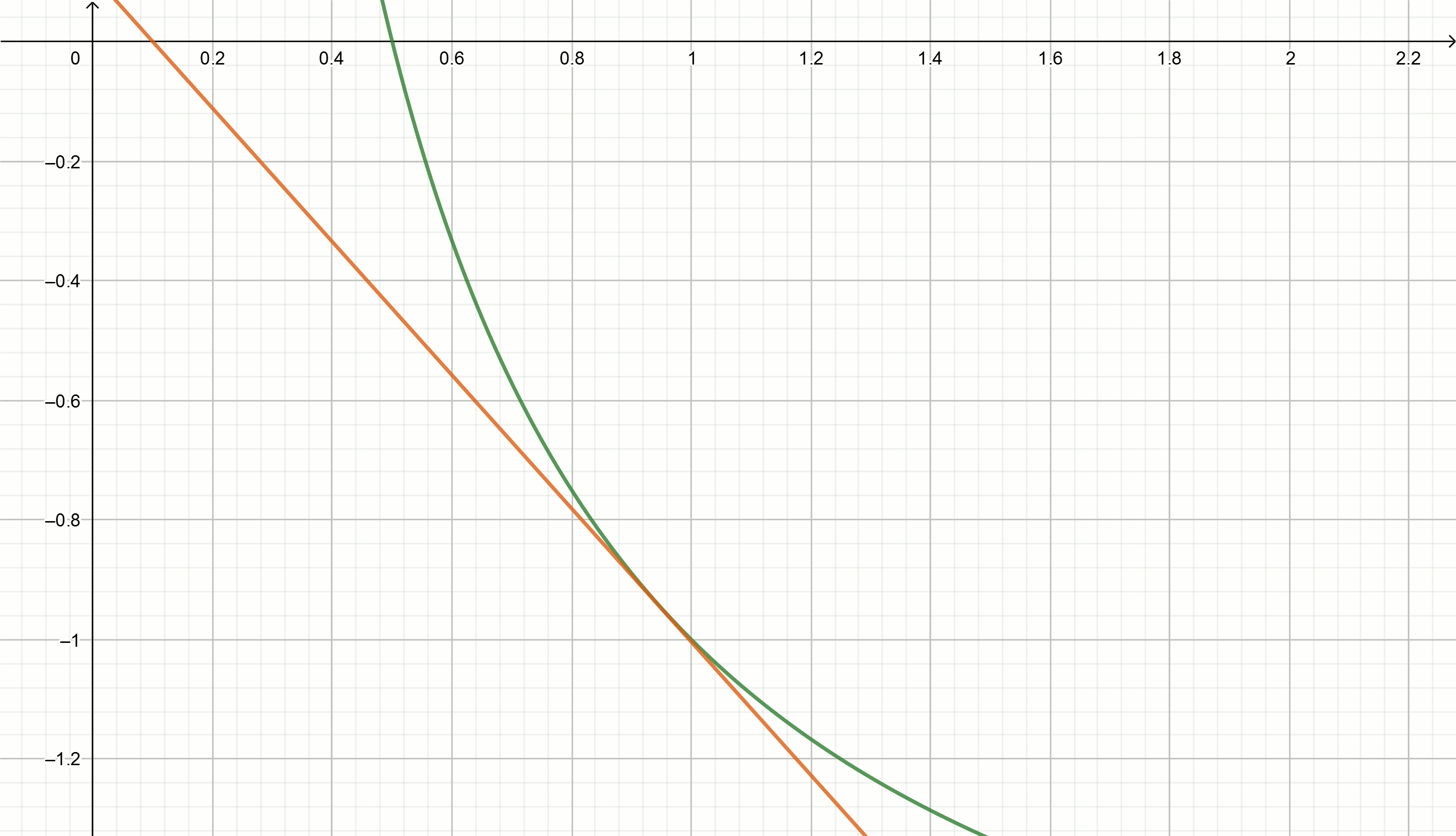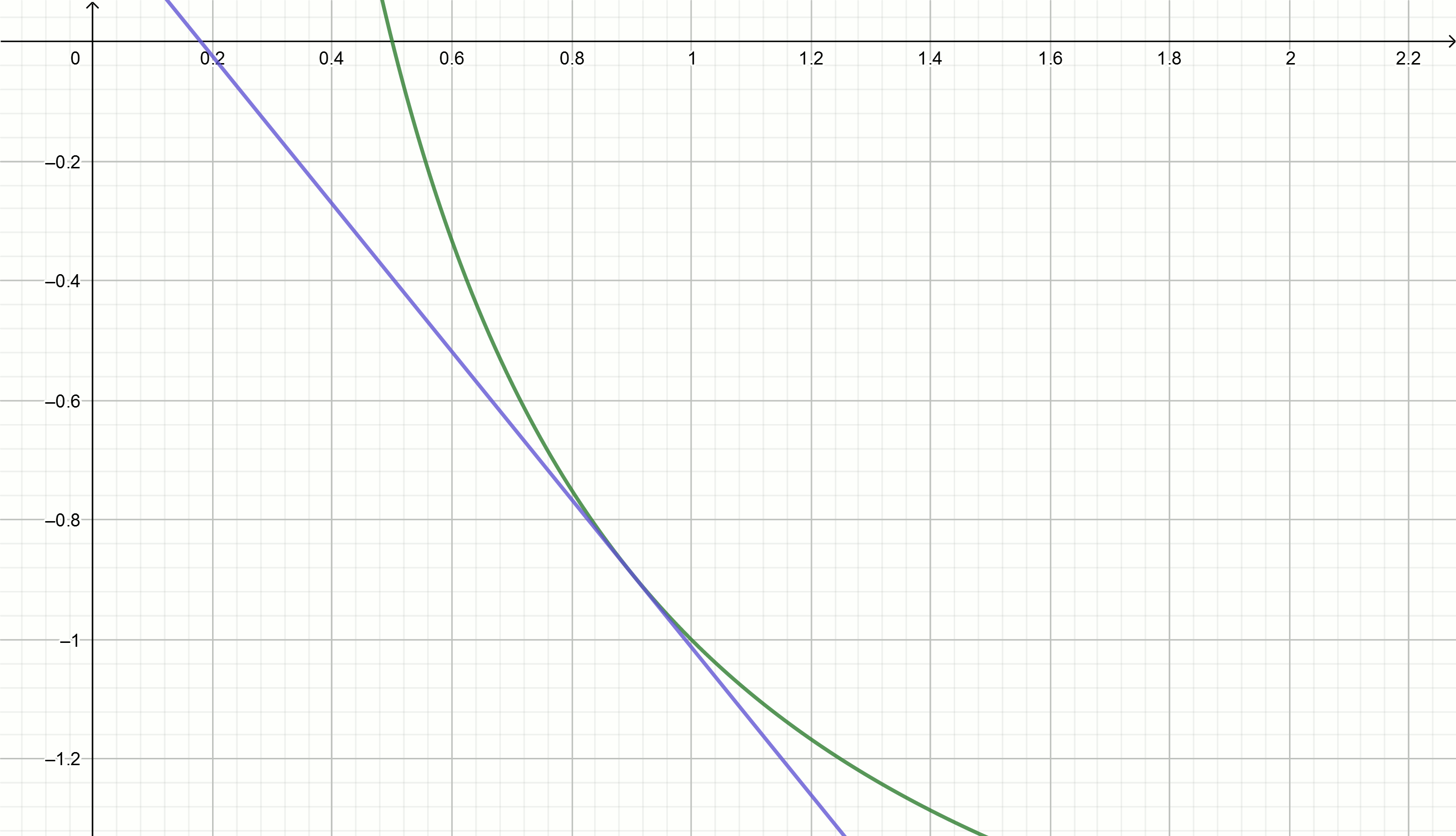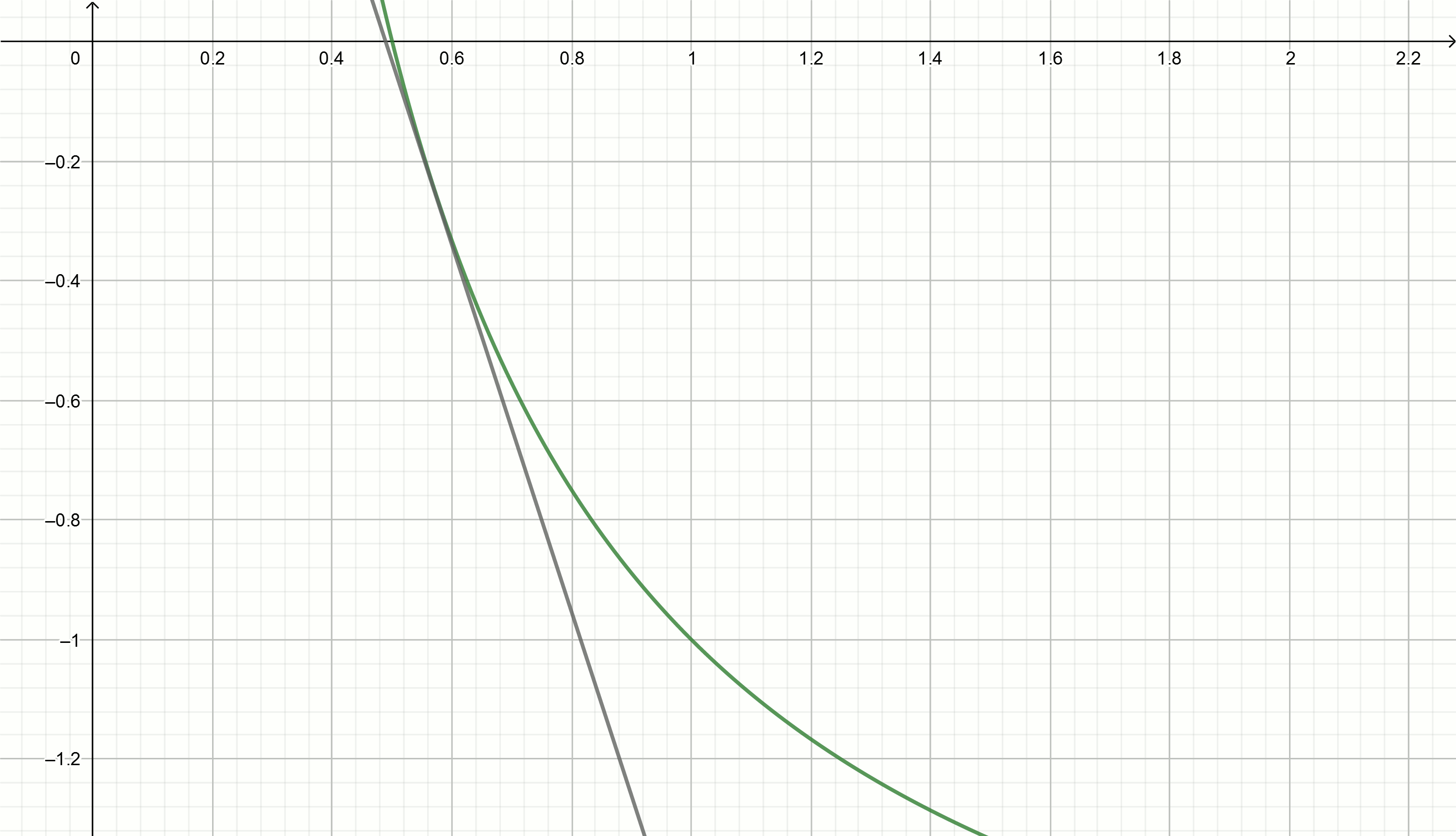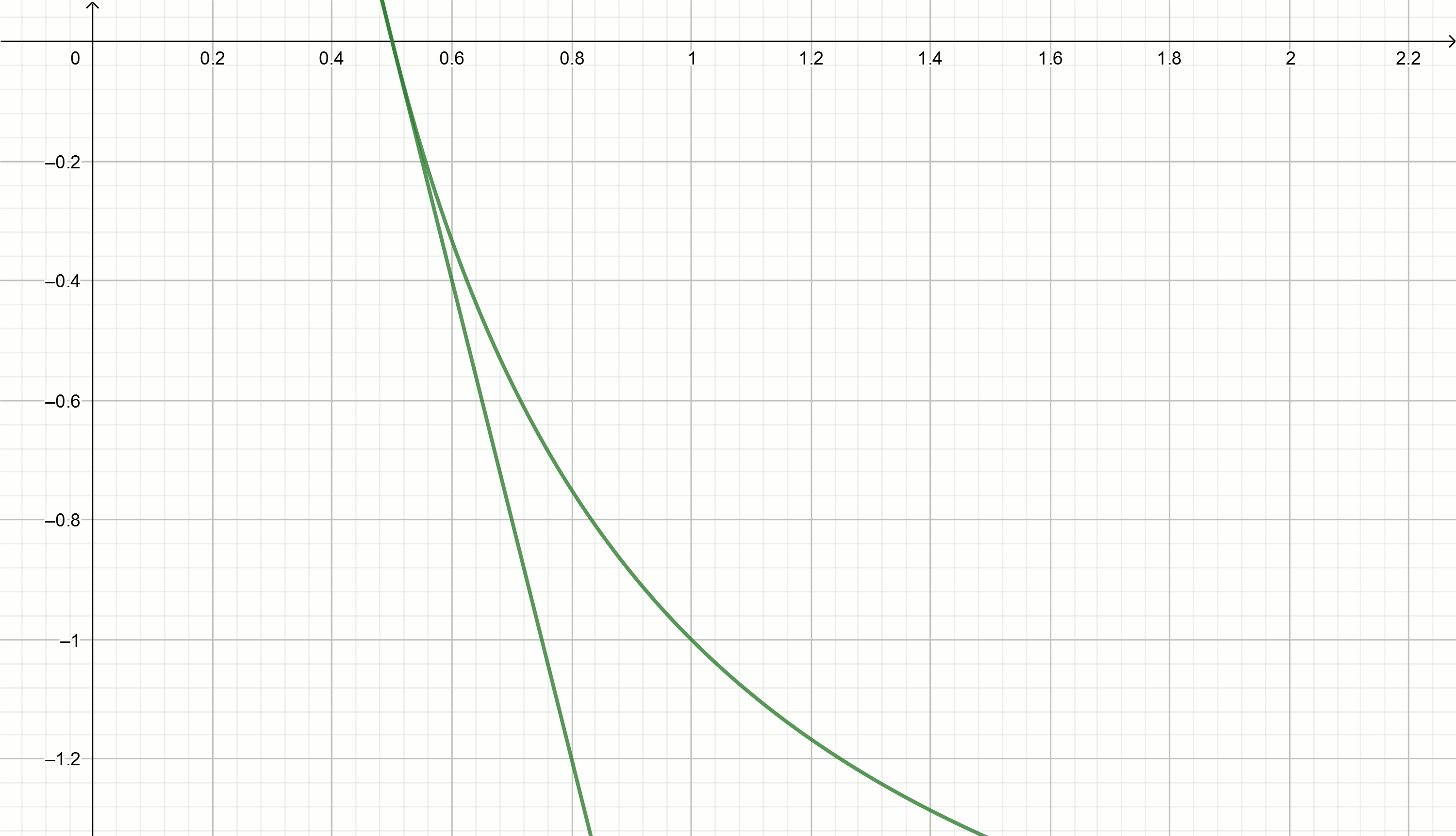
Crie esses gráficos


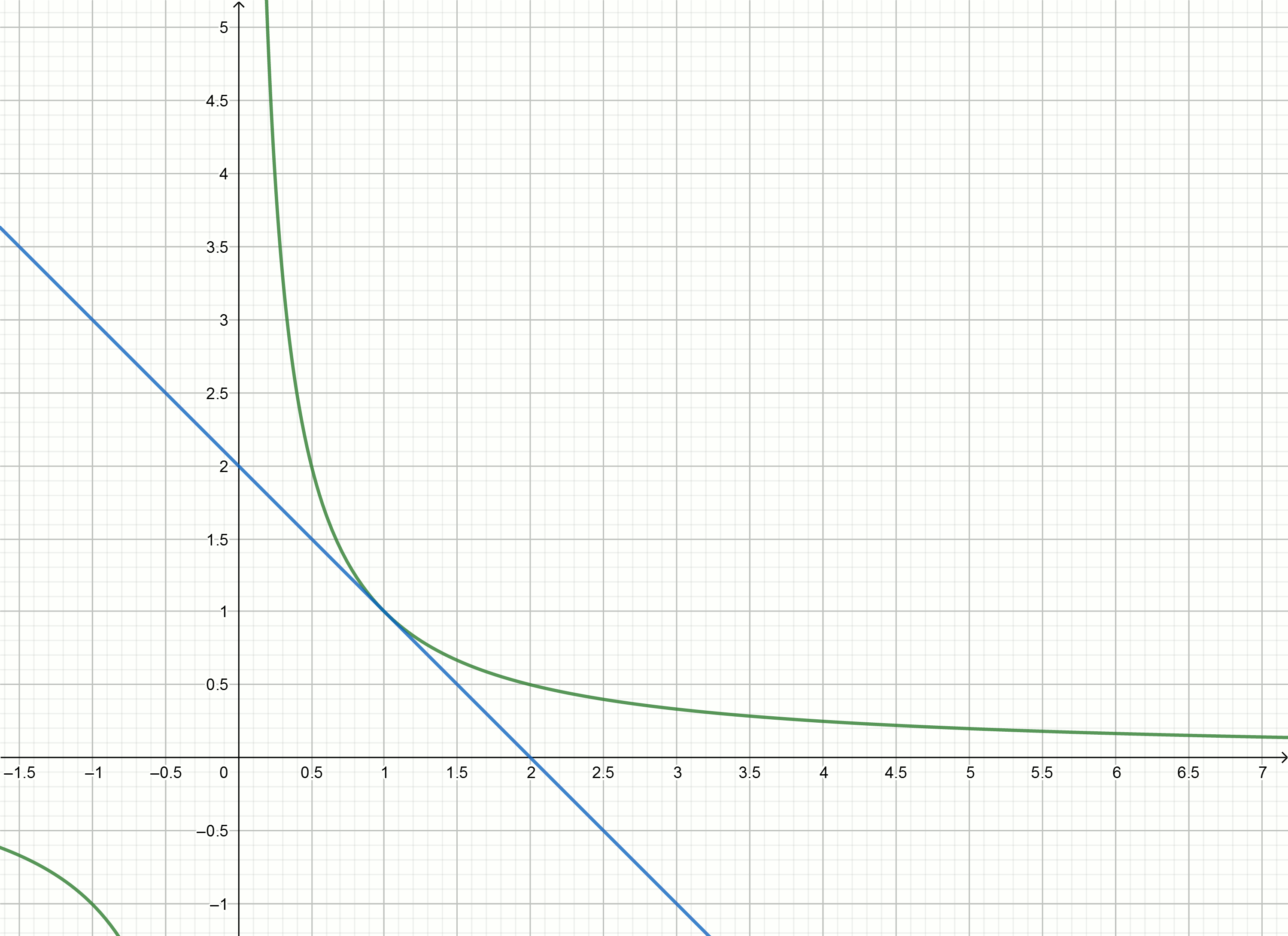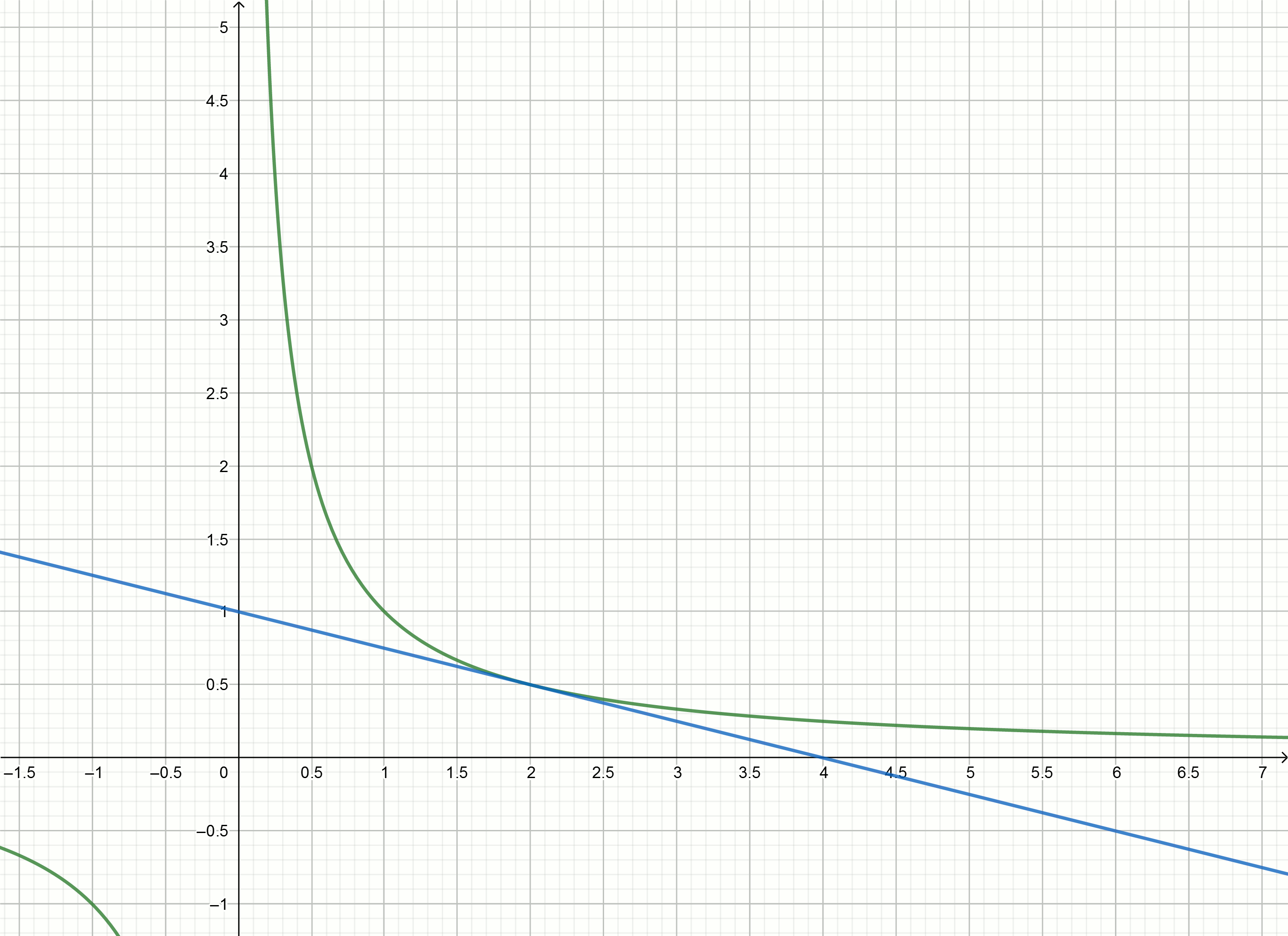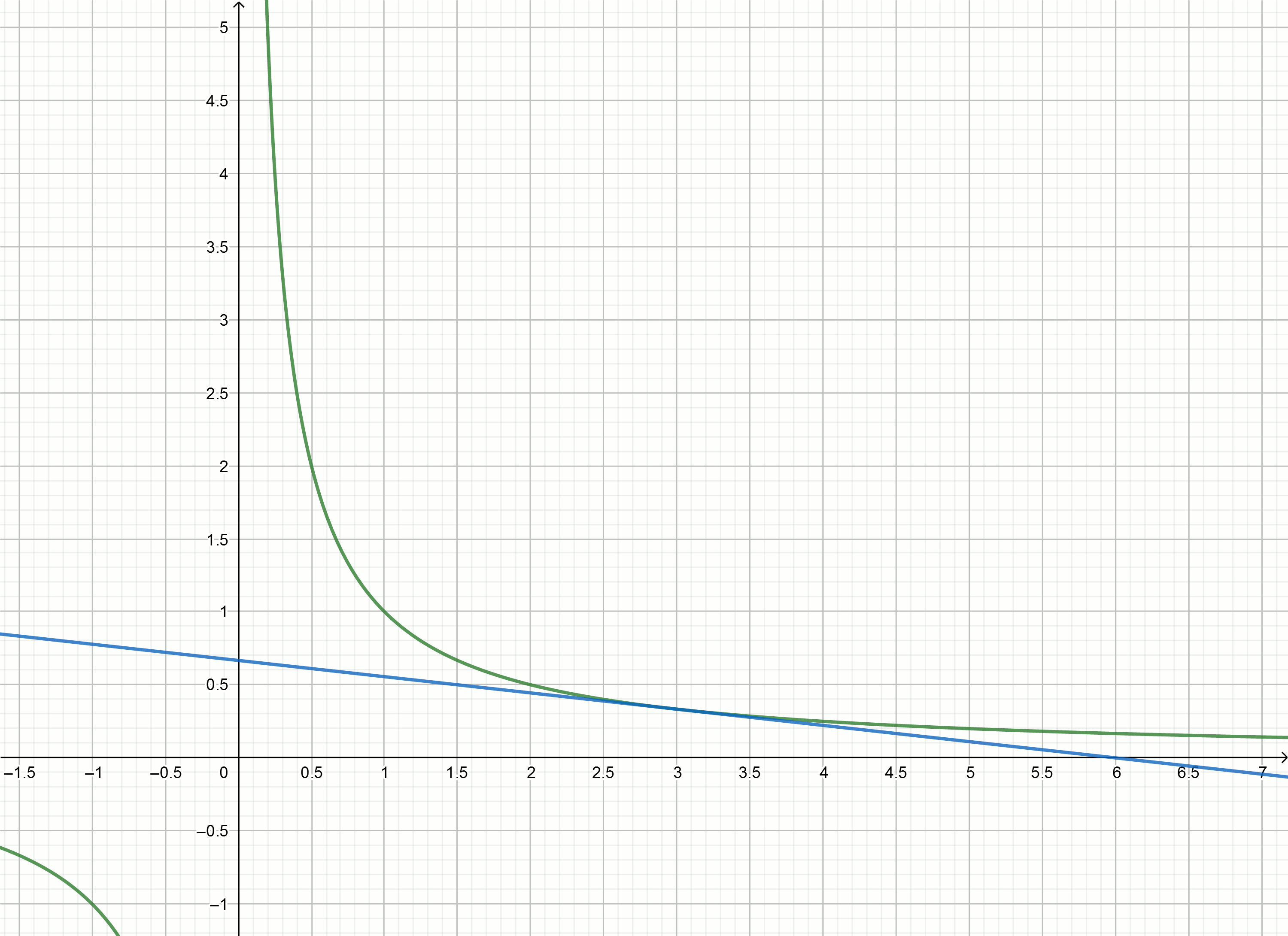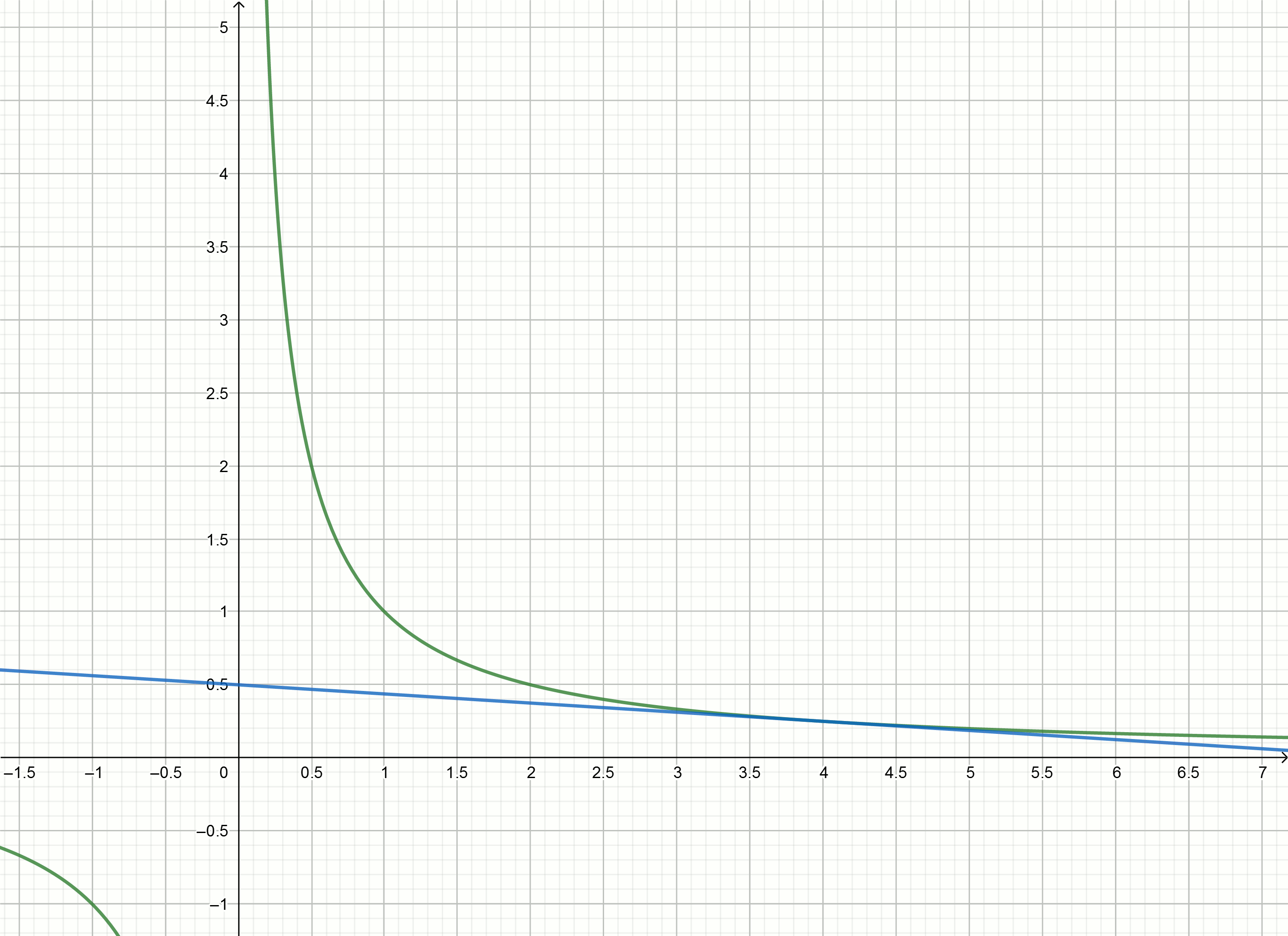
Se você mover a hipérbole para baixo para $$$\ alpha$ , então ele cruza o eixo da abcissa no ponto $$$\ frac {1} {\ alpha}$ .
A equação tangente é convertida em $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}} - \ alpha$
Além disso, igualando a equação da tangente a zero e expressando $$$x$ nós obtemos a equação $$$x = x_ {0} - \ frac {f (x_ {0})} {f '(x_ {0})}$

Em vez disso $$$f (x_ {0})$ substituto $$$\ frac {1} {x_ {0}} - \ alpha$
Em vez disso $$$f '(x_ {0})$ substituto $$$- \ frac {1} {x_ {0} ^ {2}}$

Temos a expressão $$$x = x_ {0} + (\ frac {1} {x_ {0}} - \ alpha) x_ {0} ^ {2}$
Expandindo os suportes, obtemos $$$x = x_ {0} + x_ {0} - \ alpha x_ {0} ^ {2}$

Substituto $$$0,1$ na equação $$$x = x_ {0} (2- \ alpha x_ {0})$ e veja quais valores serão "executados" $$$x$ às $$$\ alpha = 2$ nós temos $$

Substituindo esses valores na equação $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}} - 2$ nós somos diretos

$$

$$y = 0,111 - \ frac {x} {0,897}$$

$$

$$y = 0,222 - \ frac {x} {0,81}$$

$$

$$y = 0,816 - \ frac {x} {0,504}$$

$$

$$y = 0.857 - \ frac {x} {0,49}$$

$$

$$y = 1,5 - \ frac {x} {0,326}$$

$$

$$y = 2 - \ frac {x} {0,25}$$

Extração de raiz quadrada

Voltando às expressões irracionais, consideramos um método iterativo de extrair a raiz quadrada.
Escreveremos um algoritmo usando o método iterativo de Heron

$$

$$x_ {n + 1} = \ frac {1} {2} (x_ {n} + \ frac {a} {x_ {n}})$$

 def square_root(a,n): # a -  , n -   x0=1 #    1 arr=[] for i in range(n): arr.append(x0) #      x0=0.5*(x0+a/x0) #      return arr print square_root(2,10) 

codepad.org

Cálculo da raiz quadrada usando frações continuadas usadas por Rafael Bombelli

Para encontrar o valor $$$\ sqrt {n}$ , primeiro, definimos toda a sua aproximação: $$$\ sqrt {n} = a \ pm r$ onde $$$0 <r <1$ . Então $$$n = (a \ pm r) ^ {2} = a ^ {2} \ pm 2ar + r ^ {2}$ . A partir daqui, é fácil deduzir que $$$r = {\ frac {| n-a ^ {2} |} {2a \ pm r}}$ . Substituindo a expressão resultante na fórmula $$$\ sqrt {n} = a \ pm r$ , obtemos uma expansão contínua da fração:

$$

$$a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}}$$

Então, podemos escrever o algoritmo de extração de raiz quadrada usando decomposição em uma fração contínua

 def square_root(n,a,n_count): # n- , a -    x0=a #    a arr=[] for i in range(n_count): #       a arr.append(x0-a) #  a x0=2*a+(na*a)/x0 return arr print square_root(2.0,1.0,10) 

codepad.org

Em geral, números reais e complexos, bem como funções de uma ou mais variáveis, podem ser numeradores e denominadores privados.
O método de extrair a parte inteira permite representar um número irracional na forma de uma fração contínua infinita com unidades nos numeradores (numeradores freqüentes iguais à unidade).
Aqui está um exemplo de uma expansão fracionária contínua de um número $$$\ sqrt {5}$ do livro "Álgebra"

$$

$$\ sqrt {5} -2 = \ frac {(\ sqrt {5} -2) (\ sqrt {5} +2)} {\ sqrt {5} +2} = \ frac {1} {\ sqrt { 5} +2}$$

Desta maneira $$$\ sqrt {5} = 2+ \ frac {1} {\ sqrt {5} +2}$

Selecione a parte inteira do número $$$\ sqrt {5} +2: E (\ sqrt {5} +2) = 4$ . Meios $$$\ sqrt {5} +2$ pode ser representado como $$$4 + \ alpha$ . Está claro que $$$\ alpha = \ sqrt {5} + 2-4 = \ sqrt {5} -2$ portanto $$$\ sqrt {5} + 2 = 4 + \ sqrt {5} + 2$ . Mais uma vez, destruímos a irracionalidade no numerador do segundo termo:

$$

$$\ sqrt {5} -2 = \ frac {1} {\ sqrt {5} +2}$$

O resultado é:

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}$$

Vamos fazer outra etapa semelhante:

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}}$$

É fácil ver que o processo de isolamento de toda a peça e a formação de uma fração contínua neste exemplo não tem fim. Em cada novo denominador aparecerá $$$4$ e termo $$$\ sqrt {5} -2$ . Portanto, é claro que $$$\ sqrt {5}$ é representado como uma fração contínua infinita:

$$

$$\ sqrt {5} = [2, 4, 4, 4, ...]$$

Hipótese

Se $$$d \ in \ mathbb {N}, \ sqrt {d} \ notin \ mathbb {N}$ então a fração continuada do número $$$\ sqrt {d} + [\ sqrt {d}]$ puramente periódico.
Galois evarista provou essa hipótese.

I.e. se à parte não periódica da fração $$$[1; 2,2,2, ...] = \ sqrt {2}$ adicione a parte inteira $$$[\ sqrt {2}] = 1$ então temos uma fração puramente periódica $$$[2,2,2, ...]$ .

$$$\ sqrt {3} = [1; 1,2; ...];$
$$$\ sqrt {3} +1 = [2,1, ...]$

$$$\ sqrt {5} = [2; 4,4,4, ...];$
$$$\ sqrt {5} +2 = [4,4,4, ...]$

$$$\ sqrt {6} = [2; 2,4, ...];$
$$$\ sqrt {6} +2 = [4,2, ...]$

$$$\ sqrt {13} = [3; 1,1,1,1,6, ...];$
$$$\ sqrt {13} +3 = [6,1,1,1,1,1, ...]$


Se na decomposição radicular de acordo com o método Bombelli

$$

$$\ sqrt {n} = a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ { 2} |} {2a \ pm \ cdots}}}}}}}}$$

adicionar ao primeiro termo $$$a$ , obtemos uma fração puramente periódica

$$

$$\ sqrt {n} + a = 2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}}}}$$

Resta trazer a fração para uma forma mais familiar (com unidades no numerador).
Divida o numerador e o denominador da fração por $$$| n-a ^ {2} |$ nós obtemos a expressão

$$

$$\ sqrt {n} + a = 2 a \ pm {\ frac {1} {\ frac {2a} {| na ^ {2} |} \ pm {\ frac {1} {2a \ pm {\ frac { 1} {\ frac {2a} {| na ^ {2} |} \ pm \ cdots}}}}}}}$$

Desta maneira

$$

$$\ sqrt {2} +1 = 2+ \ frac {1} {\ frac {2} {1} + \ frac {1} {2 + \ frac {1} {\ frac {2} {1} +. ..}}} = [2,2,2, ...]$$

$$

$$\ sqrt {3} +1 = 2+ \ frac {1} {\ frac {2} {2} + \ frac {1} {2 + \ frac {1} {\ frac {2} {2} +. ..}}} = [2,1, ...]$$

$$

$$\ sqrt {5} +2 = 4+ \ frac {1} {\ frac {4} {1} + \ frac {1} {4 + \ frac {1} {\ frac {4} {1} +. ..}}} = [4,4,4, ...]$$

$$

$$\ sqrt {6} +2 = 4+ \ frac {1} {\ frac {4} {2} + \ frac {1} {4 + \ frac {1} {\ frac {4} {2} +. ..}}} = [4,2, ...]$$

$$

$$\ sqrt {13} +3 = 6+ \ frac {1} {\ frac {6} {4} + \ frac {1} {6 + \ frac {1} {\ frac {6} {4} +. ..}}} = [6, \ frac {3} {2}, ...]$$

Escreveremos um programa que calcula a aproximação de fração contínua $$$[6, \ frac {3} {2}, ...]$

 #lang racket (define continued_fraction ( lambda (n) (if (= n 0) 1 (+ 6 (/ 1 (+ 3/2 (/ 1 (continued_fraction(- n 1)))))) ))) (continued_fraction 4) 

codepad.org
Na quarta etapa, obtemos $$$6 \ frac {3818} {6305}$ que é igual $$$6,60555114 ...$ enquanto $$$\ sqrt {13} +3 \ aprox. 6,60555127$ .




PS Resolva o problema (“Problemas para crianças de 5 a 15 anos”)
27 Prove que o restante da divisão de um número $$$2 ^ {p-1}$ prime ímpar
$$$p$ é igual a $$$1$
(exemplos: $$$2 ^ {2} = 3a + 1, 2 ^ {4} = 5b + 1, 2 ^ {6} = 7c + 1, 2 ^ {10} -1 = 1023 = 10 \ cdot 93)$ .
Esse problema é considerado no artigo Amazing Adventures of Continued Fractions da revista Quantum.

Livros:
"Tarefas de crianças de 5 para 15 anos" V. I. Arnold.
“O curso do cálculo diferencial e integral” G. M. Fichtenholtz
"Teoria dos números" A. A. Buchstab
"Atrás das páginas de um livro de matemática" N. Ya. Vilenkin, L. P. Shibasov, Z. F. Shibasova
"Álgebra" N. Ya. Vilenkin, R. S. Guter, S. I. Schwarzburd
Aritmética digital Ercegovac Milos D., Lang Tomas
“A estrutura e interpretação dos programas de computador” Harold Abelson, Gerald Sassman

Veja também
O artigo "Em uma tarefa que não é mais oferecida na entrevista".
Publique no blog do Spice IT Recruitment a publicação de tarefas de entrevista para várias empresas.
Tarefas para entrevistas no Yandex.
Neste vídeo, A. Savvateev resolve problemas com entrevistas na Tesla.