Para evitar a detecção por radares inimigos, caças, navios e mísseis modernos devem ter a menor área de dispersão efetiva (EPR). Cientistas e engenheiros que desenvolvem esses objetos imperceptíveis, usando métodos de eletrodinâmica computacional, otimizam a EPR e os efeitos de dispersão de objetos arbitrários ao usar radares. O objeto em questão espalha as ondas eletromagnéticas incidentes nele em todas as direções e parte da energia retorna à fonte de ondas eletromagnéticas no processo das chamadas retroespalhamento, forma uma espécie de "eco" do objeto. EPR é apenas uma medida da intensidade de um sinal de eco do radar.

Na prática, uma esfera condutora de referência é usada como um objeto para calibrar radares. Uma formulação semelhante do problema é usada para verificar o cálculo numérico da EPR, uma vez que a solução para esse problema clássico de eletrodinâmica foi obtida por Gustav Mi em 1908 .

Nesta nota, falaremos sobre a realização desse cálculo de referência usando uma formulação axissimétrica bidimensional eficaz e observaremos brevemente os princípios gerais para resolver uma ampla classe de problemas de espalhamento no COMSOL Multiphysics ^® .

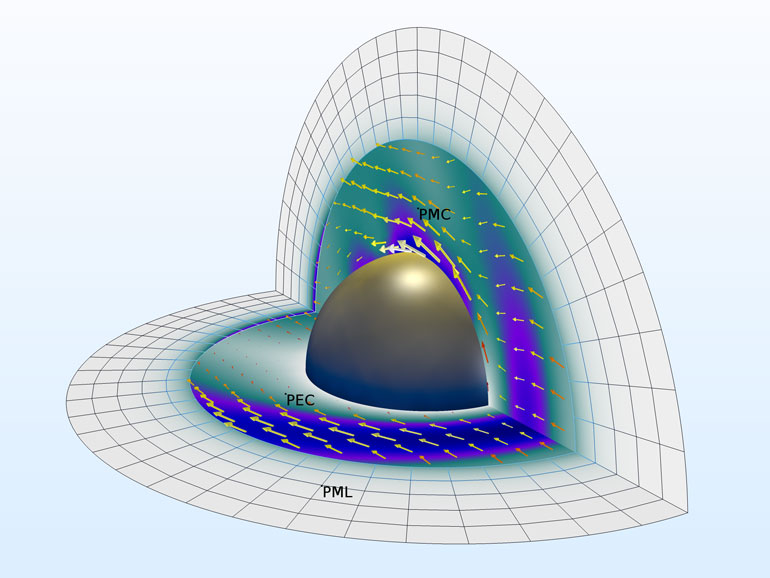
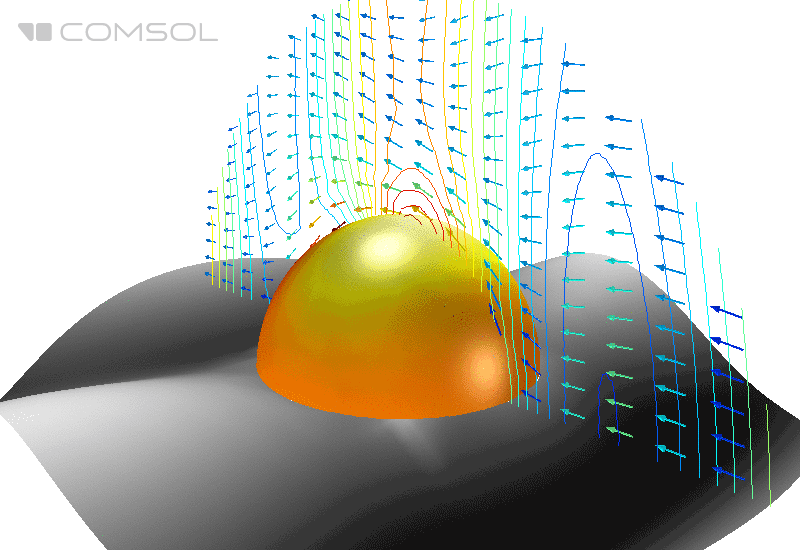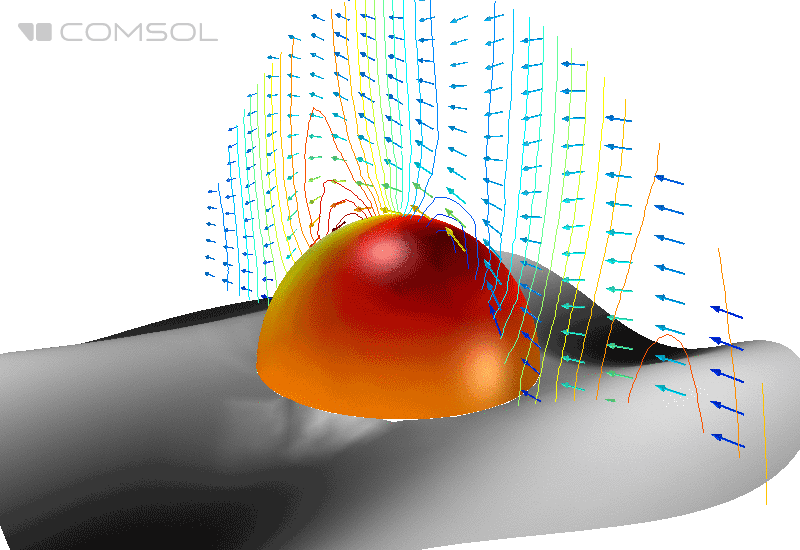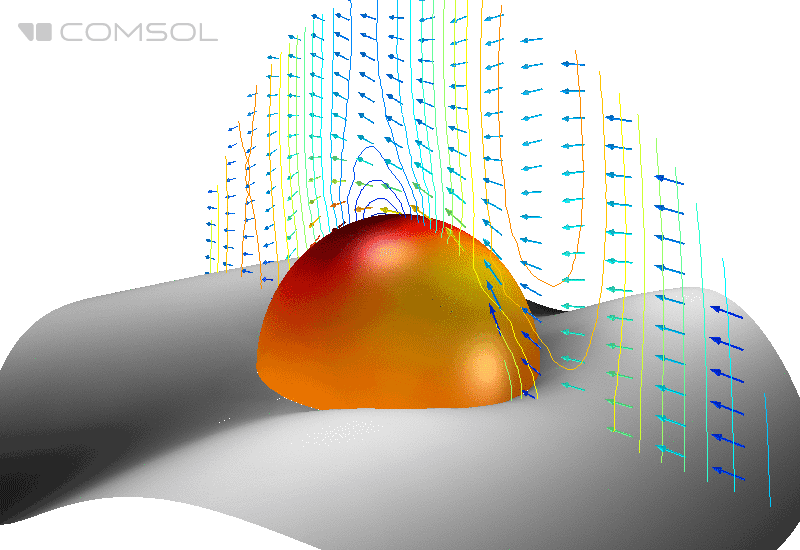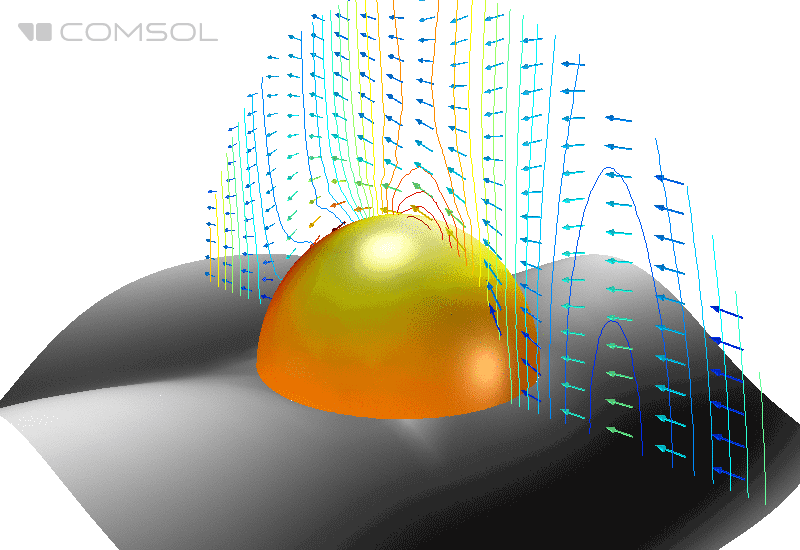
Fig. 1. Distribuição do campo elétrico (sua norma) e fluxo de energia médio (setas) em torno de uma esfera perfeitamente condutora no espaço livre.

Condução da dispersão da esfera: o tamanho é importante

No exemplo de referência clássico , uma esfera de metal perfeitamente condutora no espaço livre é irradiada com uma onda eletromagnética plana e o EPR é calculado.

Na saída, a dispersão é geralmente calculada para várias proporções do raio da esfera e do comprimento de onda, com base nas quais três áreas são distinguidas: as faixas Mi de Rayleigh , óptica e de transição.

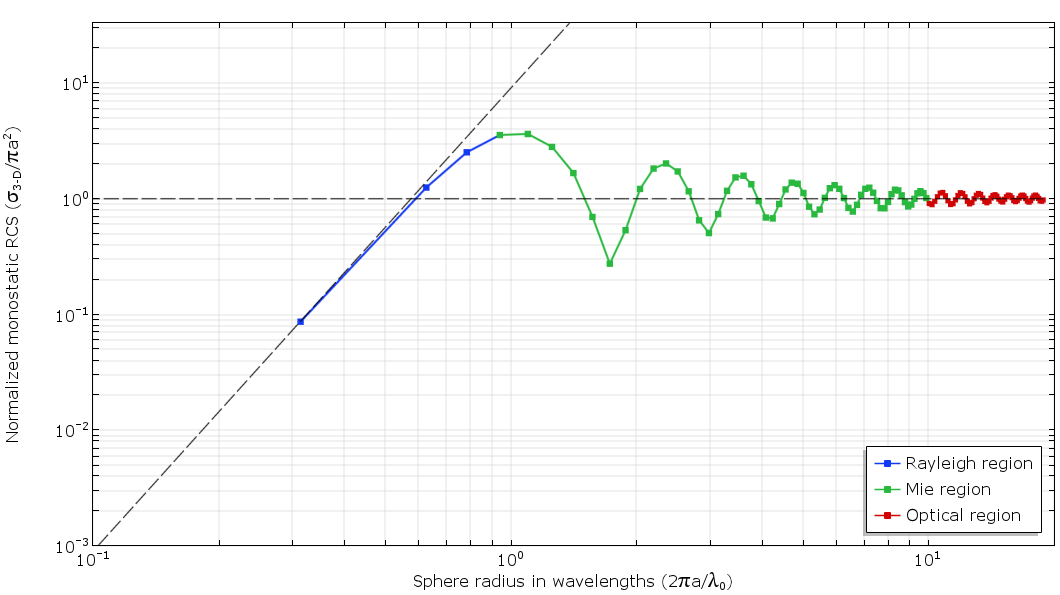
Fig. 2. Um gráfico da dependência do EPR no comprimento de onda (em uma escala logarítmica dupla). Três áreas características são distinguidas: Rayleigh, Mi e óptico. Linhas pontilhadas pretas mostram soluções assintóticas para as zonas ópticas e Rayleigh.

As características do EPR são significativamente afetadas pelo tamanho elétrico e pelas propriedades do material do objeto no qual o feixe do radar é incidente. Como o tamanho elétrico do objeto - no nosso caso, a esfera - diminui ao passar do alcance óptico para a região de Rayleigh (através da banda M), os métodos assintóticos não fornecem precisão suficiente para levar em consideração a contribuição de todos os fenômenos físicos. Para obter resultados precisos, o problema deve ser resolvido usando técnicas de onda completa .

Em um cenário tridimensional, mesmo levando em consideração o uso de camadas perfeitamente combinadas (Perfectly Matched Layers - PML), que efetivamente limitam o domínio computacional e simulam limites abertos e condições de simetria, um cálculo com resolução detalhada em frequência / comprimento de onda pode demorar um pouco.

Definindo condições de simetria para cálculos eletrodinâmicos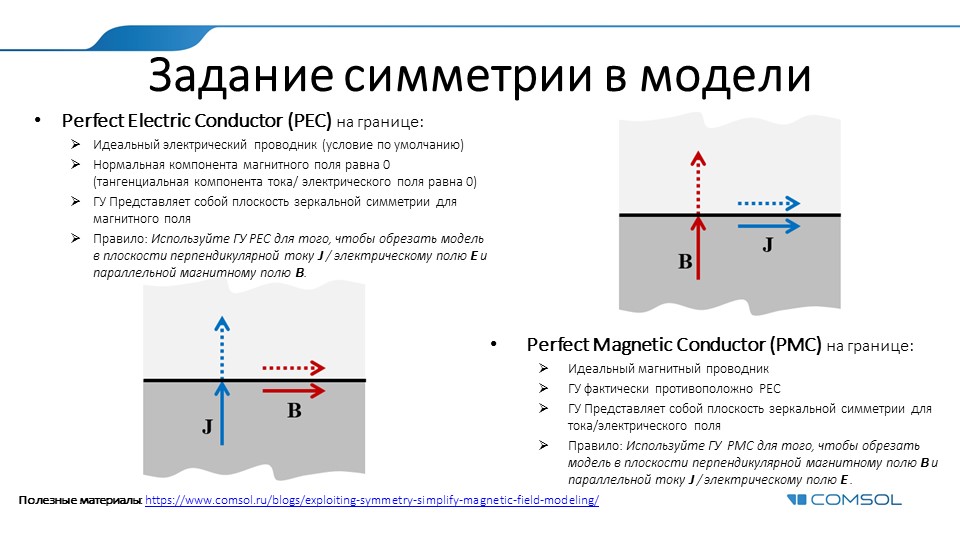

Mais detalhes aqui .

Felizmente, se o objeto é axissimétrico e dispersa as ondas isotropicamente, não é necessária uma análise 3D completa. Para analisar a propagação de ondas eletromagnéticas e o comportamento ressonante de um objeto, basta calcular sua seção transversal em uma formulação axissimétrica bidimensional sob certas condições.

Modelo axissimétrico bidimensional do processo de microondas: uma visão interna

Suponha que nossa esfera seja metálica e tenha alta condutividade. Para esta tarefa, a superfície da esfera é definida como o condutor elétrico perfeito (condutor elétrico perfeito - PEC) e sua parte interna é excluída da área de cálculo. A região ao redor é definida como um vácuo com as propriedades correspondentes do material, e a PML esférica é usada na camada mais externa, que é usada para absorver todas as ondas de saída e impedir a reflexão dos limites do domínio computacional.

Modelagem de objetos metálicos em problemas eletromagnéticos de ondas

Para a solução numérica de problemas de eletrodinâmica no domínio da frequência, existem vários métodos para a modelagem eficiente de objetos metálicos. A ilustração abaixo reflete técnicas e recomendações para o uso das condições de condição de transição de transição (TBC), condição de limite de impedância (IBC) e condutor elétrico perfeito (PEC).

Uma análise detalhada dos aspectos de aplicação de cada um deles está aqui .

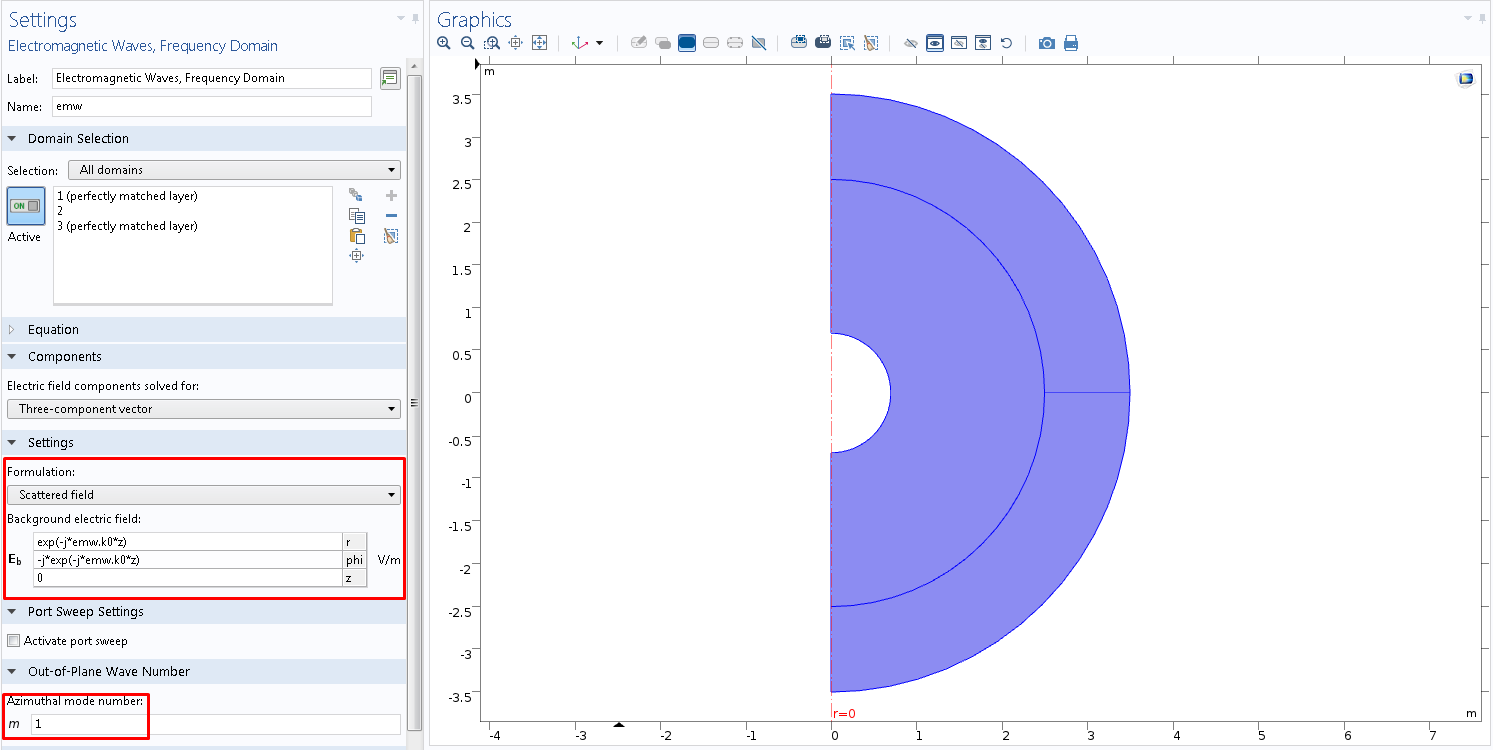
Fig. 3. Geometria para formulação axissimétrica e configuração do campo eletromagnético de fundo com polarização circular esquerda na interface gráfica COMSOL Multiphysics ^® .

No domínio computacional (exceto para PML), é especificada a excitação do campo de fundo com a polarização circular esquerda direcionada na direção negativa do eixo z (Fig. 3). Observe que o cálculo está definido apenas para o primeiro modo azimutal.

Por padrão, para tarefas de microondas no COMSOL Multiphysics ^{®, uma} grade triangular livre (ou tetraédrica para problemas em 3D) é criada automaticamente para a frequência máxima especificada para o estudo no domínio da frequência (estudo no domínio da frequência), que neste exemplo é 200 MHz. Para garantir uma resolução suficiente dos processos de onda no modelo, o tamanho máximo do elemento de malha é definido igual a 0,2 comprimento de onda. Em outras palavras, a resolução espacial é especificada como cinco elementos de segunda ordem por comprimento de onda. Em camadas perfeitamente compatíveis, a grade é construída puxando na direção da absorção, o que garante o desempenho máximo de PML.

Porque Como o número de graus de liberdade no modelo é muito pequeno (comparado à formulação tridimensional), seu cálculo leva apenas alguns segundos. Na saída, o usuário pode obter e visualizar a distribuição do campo elétrico ao redor da esfera (na zona próxima), que é a soma do fundo e dos campos dispersos.

Para esta tarefa, as características mais interessantes estão relacionadas à região do campo distante. Para incluí-los no modelo, é necessário ativar a condição Cálculo de campo distante no limite externo do domínio computacional (neste caso, a borda PML interna), que permite calcular campos na zona distante fora do domínio computacional a qualquer momento, com base nas relações integrais de Stratton-Chu. A ativação adiciona uma variável adicional - a amplitude do campo na zona remota, com base na qual, no pós-processamento, o software calcula variáveis ​​de engenharia que cumprem os padrões IEEE: potência irradiada isotropicamente, ganho (ganho conhecido como ganho, incluindo levando em consideração a incompatibilidade de entrada), coeficiente ação direcional e EPR.

De acordo com o gráfico polar, um especialista pode determinar a diretividade do campo na zona remota em um determinado plano, e um padrão de radiação tridimensional na zona remota permite um estudo mais detalhado do campo de dispersão (Fig. 4).

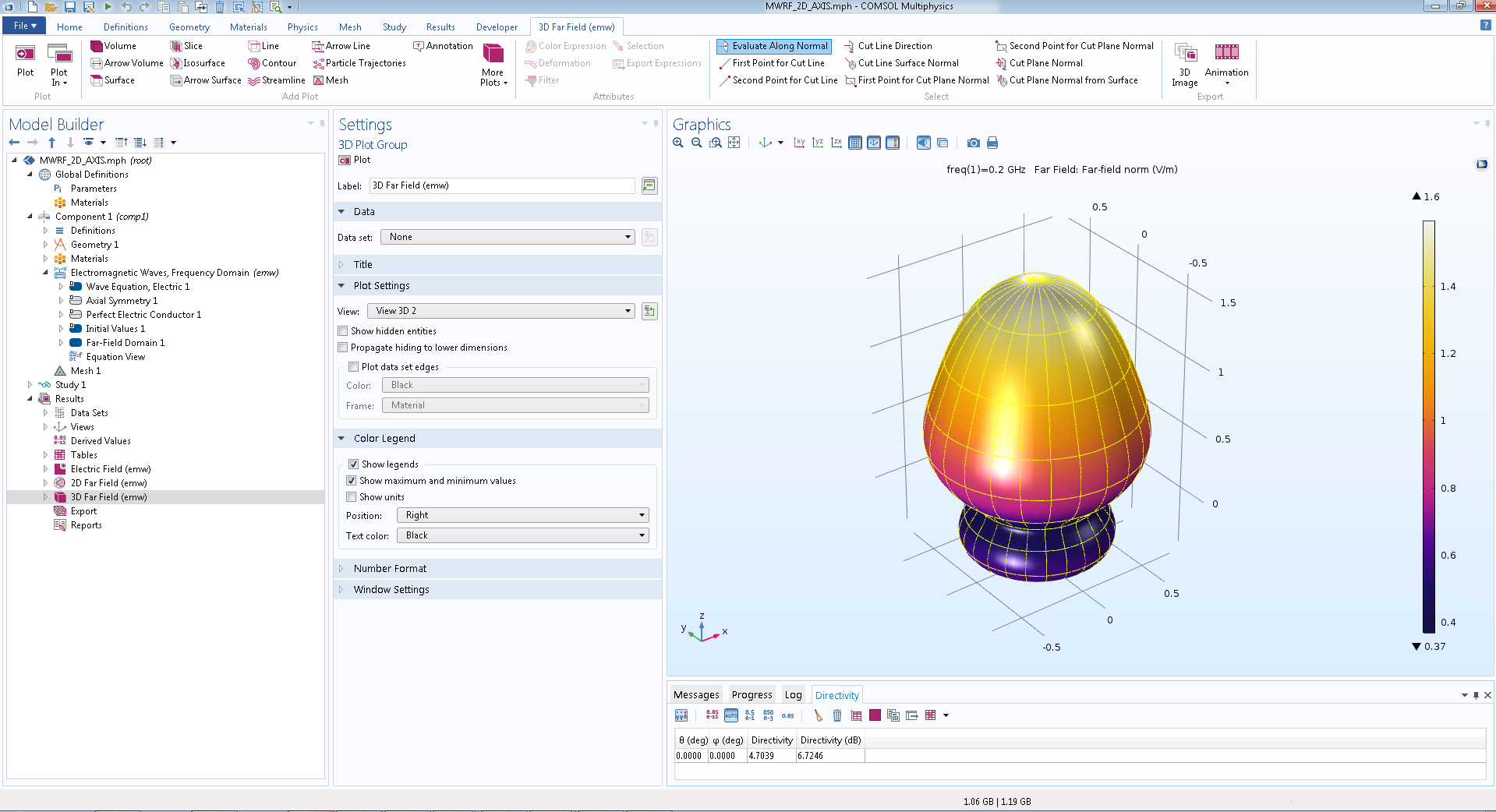
Fig. 4. Visualização tridimensional de campo na zona remota com base em um modelo axissimétrico bidimensional no COMSOL Multiphysics ^® .

Recuperação da solução para um problema tridimensional

Os resultados para o modelo "encurtado" em uma formulação axissimétrica estão relacionados ao processo de irradiar a esfera condutora com um campo circular polarizado de fundo. No problema 3d original, as características do campo de dispersão são estudadas para o caso de uma onda plana linearmente polarizada. Como contornar essa diferença?

Por definição, a polarização linear pode ser obtida adicionando a polarização circular direita e esquerda. O modelo axissimétrico bidimensional com as configurações acima (Fig. 2) corresponde ao primeiro modo azimutal (m = 1) do campo de fundo com polarização circular esquerda. A solução para o modo azimutal negativo com polarização circular direita pode ser facilmente deduzida do problema já resolvido usando as propriedades de simetria e realizando transformações algébricas simples.

Após realizar apenas uma análise bidimensional e espelhar os resultados já no processo de pós-processamento, você pode extrair todos os dados necessários, economizando significativamente os recursos computacionais (Fig. 5).

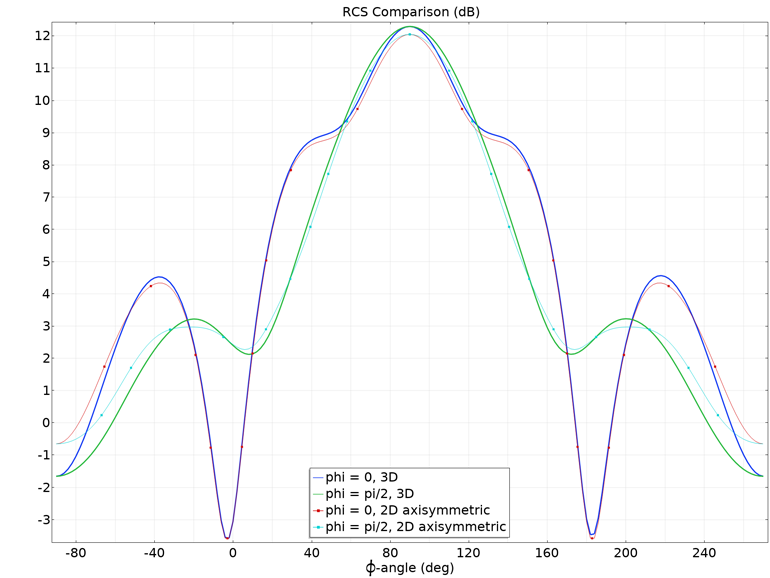
Fig. 5. Comparação da varredura da área de dispersão efetiva (em escala logarítmica) sobre os ângulos de dispersão para um cálculo tridimensional completo e o modelo axissimétrico bidimensional proposto.

O gráfico unidimensional (Fig. 5) com uma comparação EPR demonstra uma correspondência aceitável entre os modelos axissimétricos tridimensionais e bidimensionais. Uma ligeira discrepância é observada apenas na região de espalhamento para frente e para trás, próximo ao eixo de rotação.

Além disso, para a visualização dos resultados bidimensionais obtidos no espaço tridimensional, será necessária uma transformação do sistema de coordenadas de cilíndrico para cartesiano . Na fig. A Figura 6 mostra uma visualização tridimensional dos resultados para um modelo axissimétrico bidimensional.

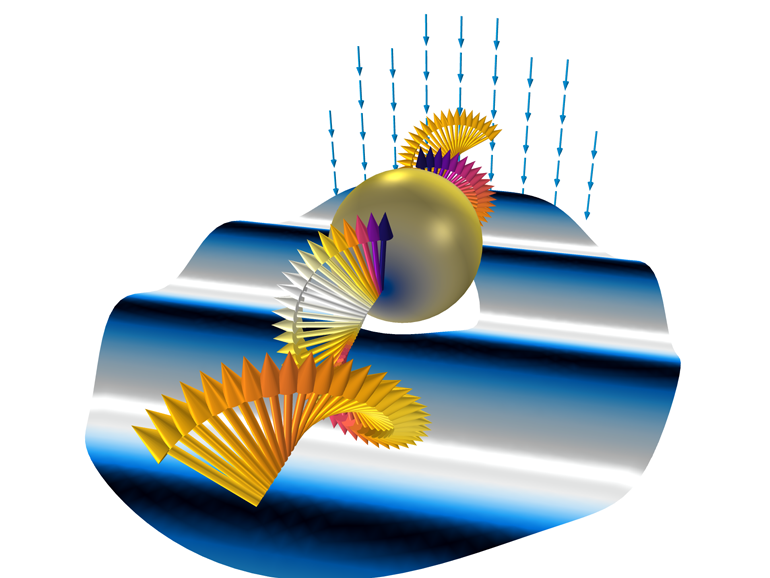
Fig. 6. Apresentação tridimensional dos resultados com base no cálculo bidimensional.

Setas girando em espiral indicam um campo de fundo com polarização circular. O gráfico na seção horizontal representa a distribuição do componente radial do campo de fundo (o processo de onda é exibido usando deformações do plano). A norma do campo elétrico total é construída na superfície da esfera. Outro diagrama de flechas mostra uma superposição de duas polarizações circulares, o que equivale a um campo de fundo com polarização linear no espaço tridimensional.

Conclusão

No processo de desenvolvimento moderno no campo da radiofísica e da tecnologia de microondas para engenheiros, técnicas eficazes de modelagem que reduzem o consumo de recursos e o tempo gasto são insubstituíveis, independentemente do método aplicado de análise numérica.

Para manter a integridade e recriar todos os efeitos físicos relevantes ao modelar um componente real com um grande tamanho elétrico, é possível simplificar o processo de cálculo numérico sem perda de precisão, resolvendo o problema em uma formulação axissimétrica bidimensional. Ao modelar e analisar objetos axissimétricos, como esferas e discos de dispersão, buzina cônica e antenas parabólicas , os cálculos para a seção transversal do dispositivo são executados várias ordens de magnitude mais rapidamente do que quando se usa o modelo tridimensional completo.

Noções básicas de modelagem de antenas no COMSOL Multiphysics

Uma breve revisão em vídeo (em russo) , que mostra exemplos de modelagem de antenas de microondas usando o módulo de radiofrequência, incluindo o cálculo das características de frequência dos parâmetros S e impedância, diagramas de Smith, estudos de correspondência, cálculo de campos na zona remota, determinação do coeficiente de diretividade (Diretividade) e ganho (ganho). Além disso, são considerados os princípios do uso de simetria, modelagem de antenas na recepção e cálculos complexos de sistemas de receptores e transmissores espaçados no espaço, avaliando a interferência eletromagnética nas antenas vizinhas e muito mais.

Nesse caso, uma formulação bidimensional simples permite reconstruir rapidamente no espaço tridimensional e estudar a dispersão do campo de fundo com polarização linear, bem como a diretividade da radiação na zona remota para antenas excitadas pelo guia de onda circular transversal TE11.

Informações Adicionais

Este material é baseado em um artigo de J. Munn. Análise numérica rápida da seção transversal de dispersão e radar , microondas e RF 3 de maio de 2018

A funcionalidade COMSOL Multiphsycics ^® também permite simular:

• Radares de forma livre e radares
• Espalhamento de banda larga com base na técnica DG-FEM (formulação no domínio do tempo usando solucionadores explícitos e subsequente conversão FFT)
• Dispersão por objetos 3D, em particular por uma nanopartícula colocada em um substrato dielétrico .

Para um conhecimento mais detalhado dos recursos de nosso pacote para os aplicativos considerados neste artigo, convidamos você a participar de nosso novo seminário on-line "Solução de problemas de dispersão no COMSOL Multiphsycics ^® " , que será realizado em 22 de agosto de 2018.

Você também pode solicitar uma versão demo do COMSOL nos comentários ou em nosso site .

GIF final: