Métodos numéricos para resolver sistemas de equações não lineares

1. Introdução

Muitos problemas aplicados levam à necessidade de encontrar uma solução geral para um sistema de equações não lineares. Nenhuma solução analítica geral do sistema de equações não lineares foi encontrada. Existem apenas métodos numéricos.

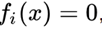
Deve-se notar um fato interessante de que qualquer sistema de equações sobre números reais pode ser representado por uma equação equivalente, se considerarmos todas as equações na forma , coloque-os quadrados e dobre-os

Para solução numérica, são utilizados métodos iterativos de aproximações sucessivas (iteração simples) e o método de Newton em várias modificações. Os processos iterativos são naturalmente generalizados para o caso de um sistema de equações não lineares da forma:

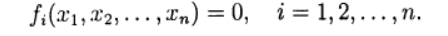
(1)

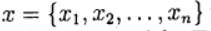
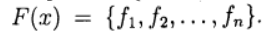
Denotar por vetor de incógnitas e definir uma função vetorial Então o sistema (1) é escrito na forma da equação:

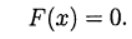
2)

Agora, voltemos ao nosso amado Python e observamos sua primazia entre as linguagens de programação que desejam aprender [1].



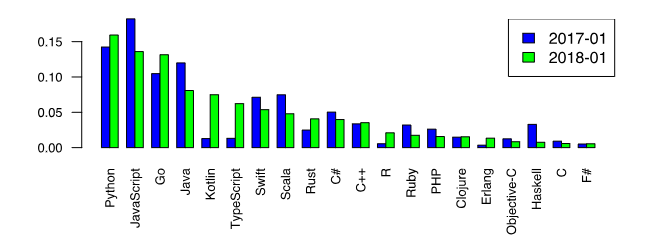
Esse fato é um incentivo adicional para considerar métodos numéricos no Python. No entanto, existe uma opinião entre os amantes do Python de que funções especiais da biblioteca, como scipy.optimize.root, spsolve_trianular, newton_krylov , são a melhor opção para resolver problemas por métodos numéricos.

É difícil discordar disso, apenas porque a variedade de módulos também elevou o Python ao auge da popularidade. No entanto, há casos em que, mesmo com um exame superficial, o uso de métodos conhecidos diretos sem o uso de funções especiais da biblioteca SciPy também fornece bons resultados. Em outras palavras, o novo é o velho esquecido.

Assim, na publicação [2], com base nos experimentos computacionais realizados, foi comprovado que a função de biblioteca newton_krylov, projetada para resolver grandes sistemas de equações não lineares, tem metade da velocidade que o algoritmo TSLS + WD
(mínimos quadrados de duas etapas) implementado pela biblioteca NumPy.

O objetivo desta publicação é comparar o número de iterações, a velocidade e, o mais importante, o resultado da resolução de um problema de modelo na forma de um sistema de cem equações algébricas não lineares usando a função da biblioteca scipy.optimize.root e o método Newton implementado usando a biblioteca NumPy.

Recursos do resolvedor Scipy.optimize.root para resolver numericamente sistemas de equações não-lineares algébricas

A função de biblioteca scipy.optimize.root foi escolhida como base de comparação, pois possui uma extensa biblioteca de métodos adequados para análise comparativa.

scipy.optimize.root ( divertido, x0, args = (), método = 'hybr', jac = nenhum, tol = nenhum, retorno de chamada = nenhum, pções = nenhum )
fun - Uma função vetorial para encontrar a raiz.
x0 - Condições iniciais para encontrar raízes

método:
é utilizada a modificação hybr - Powell do método híbrido;
lm - resolve sistemas de equações não lineares usando o método dos mínimos quadrados.
Como segue a documentação [3], os métodos broyden1, broyden2, anderson, linearmixing, diagbroyden, emocionante mixing, krylov são os métodos exatos de Newton. Os parâmetros restantes são "opcionais" e podem ser encontrados na documentação.

Métodos para resolver sistemas de equações não lineares

O material dado abaixo pode de fato ser lido na literatura, por exemplo, em [4], mas eu respeito meu leitor e, para sua conveniência, apresento a derivação do método de forma abreviada, se possível. Quem não gosta de fórmulas pula esta seção.

No método de Newton, uma nova aproximação para resolver o sistema de equações (2) é determinada a partir da solução do sistema de equações lineares :

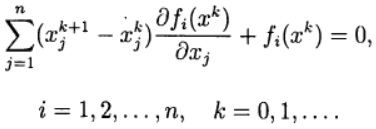
(3)

Defina a matriz de Jacobi:

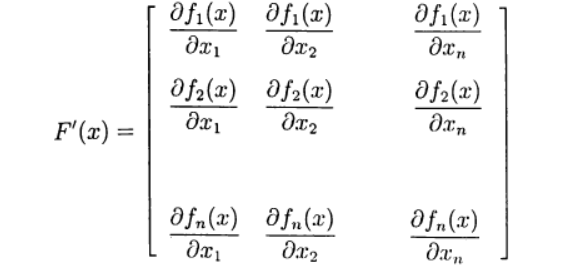
4)

Escrevemos (3) na forma:

(5)

Muitos métodos de uma etapa para solução aproximada de (2) por analogia com métodos iterativos de duas camadas para resolver sistemas de equações algébricas lineares podem ser escritos na forma:

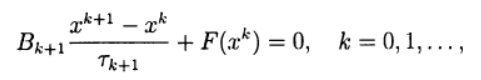
(6)

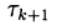
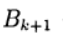
onde São parâmetros iterativos, um - uma matriz quadrada n x n tendo o inverso.

Ao usar o registro (6), o método de Newton (5) corresponde à escolha:



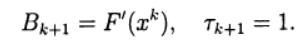
O sistema de equações lineares (5) para encontrar uma nova aproximação pode ser resolvido iterativamente. Nesse caso, temos um processo iterativo de dois estágios com iterações externas e internas. Por exemplo, um processo iterativo externo pode ser realizado de acordo com o método de Newton, e iterações internas podem ser realizadas com base no método iterativo de Seidel.

Ao resolver sistemas de equações não lineares, pode-se usar análogos diretos de métodos iterativos padrão que são usados ​​para resolver sistemas de equações lineares. O método não linear de Seidel, aplicado à solução (2), fornece:

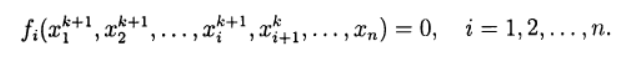
(7)

Nesse caso, cada componente da nova aproximação da solução da equação não linear pode ser obtido com base no método de iteração simples e no método de Newton em várias modificações. Assim, chegamos novamente a um método iterativo de dois estágios, no qual as iterações externas são realizadas de acordo com o método de Seidel, e as iterações internas são realizadas usando o método de Newton.

As principais dificuldades computacionais na aplicação do método de Newton para a solução aproximada de sistemas de equações não lineares estão relacionadas à necessidade de resolver um sistema linear de equações com uma matriz de Jacobi a cada iteração , e essa matriz muda de iteração para iteração. No método de Newton modificado, a matriz de Jacobi é invertida apenas uma vez:

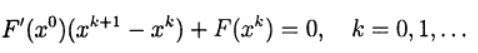
(8)

Seleção de função do modelo

Essa escolha não é uma tarefa simples, pois com um aumento no número de equações no sistema de acordo com um aumento no número de variáveis, o resultado da solução não deve mudar, pois, caso contrário, é impossível rastrear a correção da solução do sistema de equações ao comparar os dois métodos. Trago a seguinte solução para a função de modelo:

n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f 

A função f cria um sistema de n equações não lineares, cuja solução não depende do número de equações e é igual à unidade para cada uma das n variáveis.

Um programa para testar uma função de modelo com os resultados da resolução de um sistema de equações não-lineares algébricas usando a função de biblioteca optimize.root para diferentes métodos de encontrar raízes

 from numpy import* from scipy import optimize import time ti = time.clock() n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f x0 =zeros([n]) sol = optimize.root(f,x0, method='krylov') print('Solution:\n', sol.x) print('Krylov method iteration = ',sol.nit) print('Optimize root time', round(time.clock()-ti,3), 'seconds') 

Apenas um dos métodos fornecidos na documentação [3] passou no teste do resultado da resolução de uma função de modelo, este é o método 'krylov' .

Solução para n = 100:

Solução:
[1 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Iteração do método Krylov = 4219
Otimize o tempo de raiz 7,239 segundos:


Conclusão: Com um aumento no número de equações por um fator de dois, o aparecimento de erros na solução é perceptível. Com um aumento adicional de n, a solução se torna inaceitável, o que é possível devido à adaptação automática ao passo, o mesmo motivo para uma queda acentuada no desempenho. Mas este é apenas o meu palpite.

Um programa para testar uma função de modelo com os resultados da solução de um sistema de equações não-lineares algébricas usando um programa escrito em Python 3, levando em consideração as relações (1) - (8) para encontrar as raízes usando o método de Newton modificado

Solução para n = 100:

Solução:
[1 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Iteração de Newton = 13
Tempo do método de Newton 0,496 segundos

Solução para n = 200:

Solução:
[1 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1.]
Iteração de Newton = 14
Tempo do método de Newton 1,869 segundos

Para garantir que o programa realmente resolva o sistema, reescrevemos a função de modelo para evitar a raiz com o valor 1 no formato:

 n=10 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i]*sin([i]) - x[i-1] - 2*x[i+1] - 2+e**-x[i] f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f 

Temos:
Solução:
[0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1,31649896 0,6865098 0,89609091 0,98509235]
Iteração de Newton = 16
Tempo do método de Newton 0,046 segundos

Conclusão: O programa também funciona quando a função do modelo é alterada.

Agora voltamos à função inicial do modelo e verificamos uma faixa mais ampla para n, por exemplo, em 2 e 500.
n = 2
Solução:
[1 1.]
Iteração de Newton = 6
Tempo do método de Newton 0,048 segundos
n = 500

Conclusões:

Um programa escrito em Python usando o método Newton modificado, ao resolver sistemas de equações não lineares a partir da função de modelo fornecida, tem mais estabilidade de solução do que ao resolver usando a função de biblioteca optimize.root (f, x0, method = 'krylov') para o método de Krylov. Em relação à velocidade da conclusão final, é impossível desenhar devido à diferente abordagem do controle de etapas.

Referências:

1. Classificação das linguagens de programação 2018.
2. Cooper I.V., Faleychik B.V. Processos iterativos não matriciais com supressão de erro quadrático médio de raiz para grandes sistemas de equações não lineares.
3. scipy.optimize.root.
4. Vabishchevich P.N. Métodos numéricos: Oficina computacional. - M: Book House "LIBROCOM", 2010. - 320 p.