A transmissão instantânea de informações é possível? Experimentos de partículas emaranhadas quânticas

Bom dia a todos!
Continuamos a considerar as possibilidades da mecânica quântica para transmitir informações usando a correlação de partículas emaranhadas quânticas. Ao contrário dos métodos clássicos de comunicação, o uso de partículas emaranhadas quânticas oferece o potencial de transmitir informações instantaneamente a longas distâncias. A dificuldade está em encontrar maneiras de codificar e decodificar as informações transmitidas. Este artigo é dedicado a encontrar soluções para esse problema e a possibilidade de criar uma instalação experimental. Se você também está interessado nesta tarefa - bem-vindo ao gato!

Deixe-me lembrá-lo de que, no último artigo , consideramos um dos esquemas possíveis para a transmissão de informações entre dois objetos remotos. Em particular, foi considerado um esquema óptico com divisores de feixe para obter interferência, bem como um esquema de detecção e apagamento quântico usando dois conversores descendentes. Nos comentários, houve muitas discussões sobre a operacionalidade desse esquema, além de críticas por parte do usuário de que o uso de conversores descendentes leva à interação com a partícula original, mudança de fase do padrão de interferência e outras conseqüências desagradáveis. Não excluo essa possibilidade; portanto, após um exame detalhado, decidi excluir o uso de conversores descendentes e construir um circuito usando polarizadores circulares e lineares. No futuro, posso dizer que esta solução tem suas próprias dificuldades, devido às quais é impossível obter uma imagem de interferência. Para resolver essas dificuldades, usaremos a abordagem elegante resultante das consequências da própria mecânica quântica. Sou profundamente grato a todos que participaram da discussão do último artigo. Seus argumentos e críticas me ajudaram a entender melhor as dificuldades envolvidas, buscar mais informações e encontrar novas soluções.

Para começar, considere uma configuração experimental real . O feixe de laser atinge um dispositivo óptico não linear: um cristal de beta-borato de bário (BBO), devido ao qual um fóton é convertido em dois fótons emaranhados de frequência mais baixa. Um processo conhecido como espalhamento paramétrico espontâneo. O par resultante de fótons segue caminhos diferentes, um dos quais vai diretamente para o detector 1 , e o segundo passa por uma fenda dupla e entra no detector 2 . Ambos os detectores estão conectados ao circuito de coincidência, garantindo que apenas pares emaranhados de fótons sejam levados em consideração. Um motor de passo move o segundo detector e escaneia a área alvo, criando um mapa de intensidade que forma um padrão familiar de interferência.


Para um fóton passando por uma fenda dupla, polarizadores circulares são colocados na frente de cada fenda, criando polarização da luz no sentido horário ao passar por uma fenda e polarização no sentido anti-horário ao passar por outra fenda. Os fótons que passam pelo polarizador no sentido horário não podem passar pelo polarizador direcionado no sentido anti-horário. E os fótons que passam pelo polarizador no sentido anti-horário, respectivamente, não podem passar pelo polarizador direcionado no sentido horário. Os polarizadores circulares rotulam os fótons, destruindo o padrão de interferência no segundo detector ( Leis de Fresnel-Arago ).

Em seguida, um polarizador linear é introduzido no caminho do primeiro fóton, o que permite obter uma polarização diagonal dos fótons. O emaranhamento também fornece polarização diagonal adicional em seu parceiro, que passa por um espaço duplo. Isso muda o efeito dos polarizadores circulares - agora todo fóton é capaz de passar pelos polarizadores circulares no sentido horário e anti-horário. Assim, não é mais possível determinar qual caminho os fótons percorreram e as margens de interferência são restauradas.

Considere isso com mais detalhes no exemplo a seguir. Imagine Alice usando polarização linear ou circular no primeiro detector, afetando instantaneamente os resultados de Bob no segundo detector. Suponha que um cristal BBO produz o seguinte estado:


Se Alice coloca um polarizador circular na frente de um detector que filtra fótons polarizados no sentido horário, cada vez que Alice mede um fóton, o fóton Bob correspondente necessariamente tem uma polarização no sentido horário:


Como Bob colocou filtros polarizadores opostos perto de cada fenda, sabemos que esses fótons só podem passar (digamos) pela primeira fenda. A partir dessa lacuna, eles caem na tela de acordo com a função de onda:


onde a é a distância entre os slots, d é a distância entre os slots e a tela e x é a distância do meio da tela. A intensidade da luz na tela (o número de fótons) será proporcional ao quadrado da amplitude dessa onda, ou seja,


Da mesma forma, quando Alice mede um fóton com uma polarização no sentido anti-horário, o fóton Bob correspondente é polarizado no sentido anti-horário, que só pode passar pela segunda fenda e entrar na tela com uma função de onda


Observe que a única diferença é o sinal a / 2, porque o fóton foi emitido de outra fenda. Na tela, também veremos um ponto - mas este é outro ponto que é deslocado à distância a . Há um ponto importante: se Bob nunca descobre qual polarização Alice aplicou, então Bob realmente vê a soma de duas intensidades em sua tela:


uma vez que ambos são produzidos em quantidades iguais por cristal. Bob pode distinguir apenas dois picos em seus dados. Somente depois de receber os resultados da medição de Alice, ele pode ver que, para o conjunto de fótons em que Alice mediu a polarização no sentido horário, o subconjunto dos fótons de Bob foi distribuído de acordo com e para um conjunto de fótons, em que Alice mede a polarização no sentido anti-horário, um subconjunto dos fótons de Bob é distribuído de acordo com

(dois picos e sua soma quando Alice mede a polarização dos fótons usando um polarizador circular)

Agora considere a situação em que Alice usará um polarizador linear em vez de circular. A primeira coisa a fazer é escrever a função de onda do sistema em termos de estados de polarização linear:


Quando Alice usa um polarizador horizontal, a função de onda de fótons de Bob fica em um estado de superposição de polarização no sentido horário e anti-horário. Isso significa que o fóton pode realmente passar pelas duas fendas! Quando atingidos na tela, obtemos a amplitude da onda

e sua intensidade

onde representa a diferença de fase entre duas funções de onda na posição x na tela. Agora a tela realmente tem uma imagem de interferência! Da mesma forma, se Alice usa um polarizador vertical, a amplitude das ondas de fótons de Bob é

e intensidade

E, novamente, um padrão de interferência aparece na tela, mas mudou ligeiramente em relação ao anterior devido à diferença de fase dos fótons que cruzam os polarizadores horizontal e vertical.

Então, Alice pode enviar uma mensagem para Bob, codificando sua mensagem usando polarizadores lineares e circulares? Infelizmente não. Como Bob não foi informado sobre qual polarização Alice havia usado, tudo o que vê é a soma de duas interferências. Portanto, o resultado


é novamente uma mancha.


(dois padrões de interferência e sua soma quando Alice mede a polarização de fótons usando um polarizador linear)

As correlações variam dependendo do experimento que Alice realiza. Apesar do fato de a imagem geral ser a mesma, os dois subconjuntos produzem correlações radicalmente diferentes: se Alice usa polarização linear, a imagem completa na tela é formada a partir de dois padrões de interferência, e se Alice usa polarização circular, a imagem é a soma de dois picos.

Para detectar interferências, você precisará modificar esse experimento da seguinte maneira: em vez de dois slots com polarizadores circulares, será necessário instalar um interferômetro Mach Zehnder. Vamos considerar em mais detalhes o princípio de operação deste interferômetro e tentar descobrir o que muda quando ele é usado.

INTERFERÔMETRO MACH ZENDER
Na entrada do interferômetro, há um espelho translúcido que divide o fluxo de luz em dois feixes. Refletindo a partir de dois espelhos opacos, eles são reunidos em um segundo espelho translúcido. Se o fóton fosse uma partícula clássica, então, com uma probabilidade de 50%, poderia passar pelo primeiro espelho translúcido, e com uma probabilidade de 50%, será refletido a partir dele.
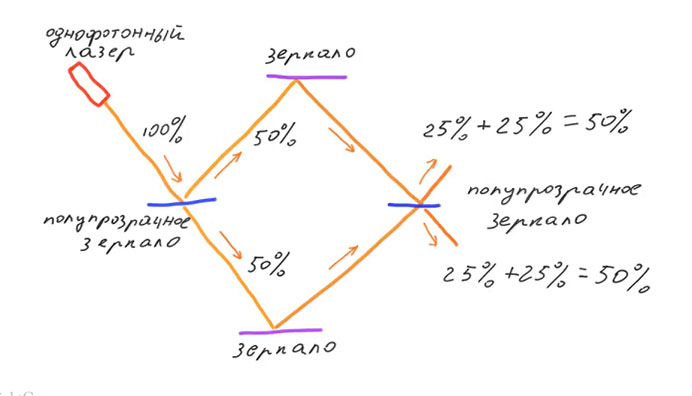
Suponha que um fóton passe pelo primeiro espelho translúcido e se mova ao longo do ramo inferior. No segundo espelho translúcido, ele também pode passar ou ser refletido com uma probabilidade de 50%. Ou seja, a contribuição do ramo inferior é a seguinte: 25% do número inicial de fótons se moverão para cima após o segundo espelho translúcido e 25% para baixo. Se o fóton refletido no primeiro espelho translúcido e foi ao longo do ramo superior, então no segundo espelho translúcido ele pode passar ou ser refletido. A contribuição do ramo superior também será de 25% para cima e para baixo. A probabilidade total é a soma das contribuições de dois ramos e é de 50% que o fóton se move para cima depois de passar pelo segundo espelho translúcido e de 50% para baixo.

Se realizarmos um experimento real, veremos que todos os fótons que passam pelo dispositivo se moverão para baixo. Nem um único fóton se move após o segundo espelho translúcido. O fato é que, tendo passado o primeiro espelho translúcido, um fóton será descrito não por probabilidades clássicas, mas por uma superposição quântica.

Denotamos pelos vetores cetônicos básicos com setas duas direções possíveis do fóton: para cima e para baixo. Então, inicialmente, o fóton será descrito pelo vetor de estado "inativo". Após passar pelo primeiro espelho translúcido, o fóton estará em uma superposição dos vetores de base para cima e para baixo. Essa superposição é outra realização física do qubit, juntamente com a rotação do elétron e a polarização do fóton.
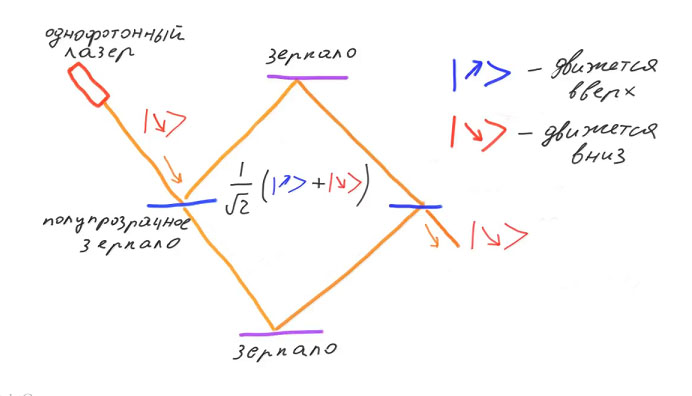
Os quadrados do valor absoluto das amplitudes de probabilidade serão as probabilidades clássicas da passagem e reflexão de um fóton. Após o primeiro espelho translúcido, eles coincidirão com os clássicos: 50% que o fóton se move para cima e 50% que para baixo. Depois de passar pelo segundo espelho translúcido, as amplitudes de probabilidade alteram seus valores. Além disso, no quadro da mecânica quântica, pode-se calcular que um deles será zero e o outro. Ou seja, o fóton retornará ao estado descrito pelo vetor base abaixo. Com cem por cento de probabilidade, depois de passar pelo segundo espelho translúcido, o fóton se moverá para baixo.

Na saída do segundo espelho translúcido, nada mais do que interferência do fóton é observado. Se tentarmos descobrir qual dos braços do interferômetro o fóton realmente passou, a interferência desaparece.

EXPERIÊNCIA
Vamos tentar colocar polarizadores circulares no interferômetro Mach Zehnder. Em um braço do interferômetro, instale um polarizador circular no sentido horário. Por outro lado, ajuste o polarizador circular no sentido anti-horário. Além disso, no braço, um polarizador circular é instalado diretamente após o espelho translúcido. No braço inferior, um polarizador circular é instalado após o espelho reflexivo. O fato é que um fóton polarizado circularmente refletindo de um espelho inverte a direção da polarização. Portanto, para fótons que não são refletidos de um espelho translúcido, a polarização circular é estabelecida após a reflexão do espelho.
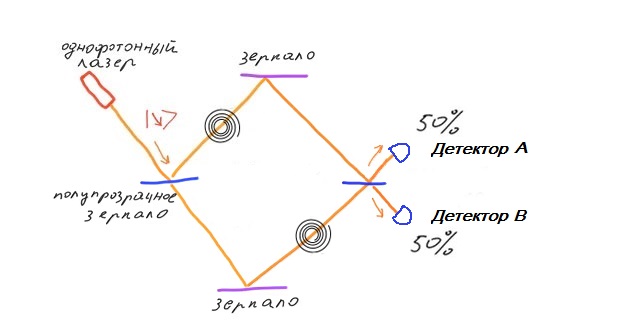
A presença de polarizadores no interferômetro fornece o potencial para determinar o caminho ao longo do qual o fóton passou. Portanto, o fóton passará ao longo do ombro superior ou ao longo do ombro inferior e nunca passará pelos dois ombros ao mesmo tempo. Consequentemente, não observamos interferência na saída. A ausência de interferência leva ao fato de que na saída obtemos 50% dos fótons direcionados para cima e 50% dos fótons direcionados para baixo.

A situação mudará se usarmos partículas emaranhadas quânticas. Digamos que um feixe de laser atinja um dispositivo óptico não linear: um cristal de beta-borato de bário (BBO), devido ao qual um fóton é convertido em dois fótons emaranhados de frequência mais baixa. O par resultante de fótons seguirá caminhos diferentes, um dos quais passa pelo polarizador e vai diretamente para o detector 1 , e o segundo passa por um interferômetro com polarizadores circulares e vai para o detector 2 ou 3 .
Se colocarmos um polarizador circular no caminho do primeiro fóton, também não veremos interferência. Assim, na saída, obtemos 50% dos fótons direcionados para cima e 50% dos fótons direcionados para baixo.
Mas se um polarizador linear localizado na diagonal for colocado no caminho do primeiro fóton, o estado emaranhado fornecerá polarização diagonal adicional em seu parceiro. A presença de uma polarização linear adicional permitirá que os fótons passem pelos dois braços e interfiram entre si. Nesse caso, a interferência terá uma diferença de fase (fótons cujos parceiros passaram pelo polarizador linear e cujos parceiros não passaram, criarão interferência na tela que é deslocada uma da outra). Apesar disso, o fóton na saída do segundo espelho translúcido retornará ao estado descrito pelo vetor base abaixo. Portanto, depois de passar pelo segundo espelho translúcido, todos os fótons se moverão para baixo.

Esse esquema de implementação é conveniente, pois não requer o estabelecimento de um padrão de coincidência de partículas emaranhadas, emitindo fótons um por um e analisando a posição de cada fóton na tela. Ao instalar ou remover um polarizador linear no caminho de partículas emaranhadas, você pode afetar instantaneamente a distribuição de seus parceiros entre os detectores 2 e 3. Basta comparar a intensidade do fluxo de luz nos dois detectores e determinar o bit de informação transmitido. Naturalmente, na saída do cristal BBO, nem todos os fótons serão entrelaçados. O número de pares emaranhados equivale a várias dezenas de por cento do total. Mas mesmo uma pequena mudança na intensidade da luz pode ser detectada pelos detectores, que descriptografarão as informações transmitidas. A segunda grande vantagem é que os pares emaranhados não estão em um estado de superposição entre si. Isso permite que eles interajam com o ambiente e não destruam as informações transmitidas, ao contrário do teletransporte quântico, quando a interação com o ar ou com um cabo óptico destrói a função de onda do fóton.

PROBLEMAS RELACIONADOS
O uso de tais esquemas alcançará um atraso mínimo ao transmitir informações a longas distâncias. A velocidade da transferência de informações pode exceder significativamente a velocidade da luz no vácuo. Alguns argumentam que o STO / GTR proíbe a transmissão de informações a uma velocidade acima da velocidade da luz. A idéia da finitude da velocidade da luz foi proposta por Poincare e derivada das fórmulas de Maxwell. Nesse caso, inicialmente era um campo eletromagnético, e depois com a mão leve de Albert Germanovich foi estendido a todos os objetos materiais maciços e sem massa. É importante enfatizar que não houve conversas sobre informações; se você abrir algum livro sobre STO / GRT, as informações não estarão presentes no formalismo matemático. Portanto, quando afirmam que o STO / GTR proíbe a transmissão de informações acima da velocidade da luz, é assumido implicitamente que não há outra maneira senão "plantar informações" em um feixe de fótons / elétrons, etc. não existe

PRINCÍPIO DE CAUSA
Um dos principais problemas da transferência instantânea de informações é a violação do princípio da causalidade. Mas você pode ver que a física moderna não requer conformidade com a causalidade no nível quântico, portanto, não está entre os postulados da física. Existem experimentos quânticos nos quais a flecha do tempo pode muito bem ser revertida. No entanto, o homem ainda não pode se recusar a cumprir a causalidade, pois isso contradiz nossa lógica.

Segundo a teoria da relatividade de Einstein, a transferência instantânea de informações permite que as informações sejam recebidas antes de serem enviadas. Por exemplo, se decidirmos enviar informações para nós mesmos, podemos realizar um experimento de forma a obter informações antes de enviá-las. Suponha que transmitiremos informações usando um par intrincado. Então um fóton passará pelo interferômetro e chegará ao detector, e o segundo fóton, por exemplo, irá para a lua, onde será refletido pelo espelho e voltará para nós.
Ao instalar ou remover um polarizador linear no caminho do segundo fóton, podemos influenciar o resultado na saída do interferômetro. Assim, observando os detectores na saída do interferômetro, saberemos antecipadamente quais informações decidimos enviar em 2,5 segundos (o tempo de vôo dos fótons para a lua e vice-versa). Isso pode levar ao "paradoxo do avô morto" quando vimos um significado e decidimos enviar o oposto.

, . , . , . , .

– . , . , . , . . . , , .

, « ». , . .

, , . . , , (.. ). .


– . , . , , . , . , . .


, . . , « », ( ) . , . , . . (, , , , ) .

, . , , . , . , 70000 . , , -. , 17 , 10-20 .

PS , , - .

Fontes:
Quantum eraser experiment

?