Construindo órbitas de corpos celestes usando Python

Sistemas de referência para determinar a órbita

Para encontrar as trajetórias dos movimentos relativos na mecânica clássica, é utilizada a suposição do tempo absoluto em todos os referenciais (inerciais e não inerciais).

Usando essa suposição, consideramos o movimento do mesmo ponto em dois quadros de referência diferentes $$$K$ e $$$K ^ {'}$ dos quais o segundo se move em relação ao primeiro a uma velocidade arbitrária $$$\ vec {V (t)} = \ ponto {\ vec {R (t)}}$ onde $$$\ vec {R (t)}$ vetor de raio que descreve a posição da origem do sistema de coordenadas $$$K ^ {'}$ em relação ao quadro de referência $$$K$ )

Vamos descrever o movimento de um ponto no sistema $$$K ^ {'}$ vetor de raio $$$\ vec {r ^ {'}} (t)$ direcionado a partir da origem do sistema $$$K ^ {'}$ para a posição atual do ponto. Então o movimento do ponto em consideração em relação ao quadro de referência $$$K$ descrito por um vetor de raio $$$\ vec {r (t)}$ :

$$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ (1)

e velocidade relativa $$$\ vec {v (t)}$

$$$\ vec {v} (t) = \ ponto {\ vec {r ^ {'}}} (t) + \ ponto {\ vec {R}} (t)$ (2)

onde $$$\ ponto {\ vec {r ^ {'}}} (t)$ - velocidade do ponto em relação ao sistema $$$K ^ {'}$ ; $$$\ ponto {\ vec {R}} (t)$ velocidade do quadro $$$K ^ {'}$ em relação ao quadro de referência $$$K$ .



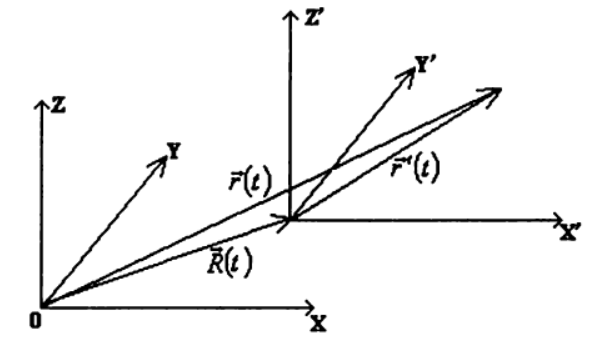
Assim, encontrar a lei do movimento de um ponto em um referencial arbitrário $$$K$ necessário:

1) definir a lei de moção do ponto - $$$\ vec {r ^ {'}} (t)$ em relação ao quadro de referência $$$K ^ {'}$ ;
2) definir a lei do movimento - $$$\ vec {R} (t)$ sistemas de referência $$$K ^ {'}$ em relação ao quadro de referência $$$K$
3) determinar a lei de moção do ponto - $$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ em relação ao quadro de referência $$$K$ .

Construção da órbita da lua no quadro de referência heliocêntrico

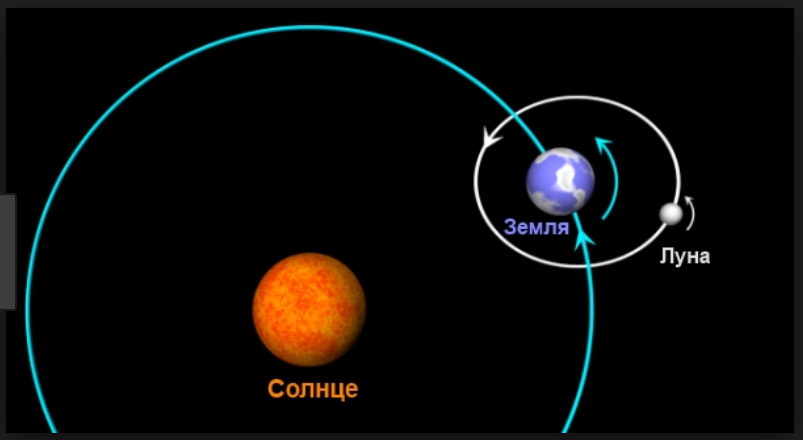
No sistema de referência heliocêntrico (sistema $$$K$ ) Terra se move em um círculo de raio
$$$R_ {1} = 1.496 \ cdot 10 ^ {8}$ km (período de circulação $$$T_ {1} = 3.156 \ cdot 10 ^ {7}$ s.). A lua, por sua vez, se move em torno da Terra (sistema K ') em torno de um círculo de raio $$$R_ {2} = 3,844 \ cdot 10 ^ {5}$ km (período de circulação $$$T_ {2} = 2,36 \ cdot 10 ^ {6}$ s Como é sabido [1,2], quando um ponto de material se move ao longo de um círculo de raio $$$R$ com velocidade angular constante $$$\ omega$ as coordenadas do vetor do raio traçadas desde a origem até a posição atual do ponto mudam de acordo com a lei:

$$

$$\ vec {R (t)} = \ binom {R \ cdot cos (\ omega \ cdot t + \ varphi _ {0})} {R \ cdot sin (\ omega \ cdot t + \ varphi _ {0})} = \ binom {R \ cdot cos (\ frac {2 \ pi} {T}) + \ varphi _ {0})} {R \ cdot sin (\ frac {2 \ pi} {T} + \ varphi _ { 0})}, (3)$$

onde $$$\ varphi _ {0}$ - a fase inicial que caracteriza a posição da partícula no momento $$$t = 0$ , que no futuro assumiremos como sendo zero. Substituindo em (3) $$$R$ em $$$R_ {1}$ e $$$R_ {2}$ e substituindo em (1), obtemos a dependência do vetor raio da lua no sistema de coordenadas heliocêntricas no tempo:

$$

$$\ vec {r (t)} = \ binom {x (t)} {y (t)} = \ binom {R_ {2} cos (\ frac {2 \ pi} {T_ {2}} t) + R_ {1} cos (\ frac {2 \ pi} {T_ {1}} t)} {R_ {2} sin (\ frac {2 \ pi} {T_ {2}} t) + R_ {1} sin (\ frac {2 \ pi} {T_ {1}} t)}, (4)$$

A expressão (4) define a órbita da Lua ( $$$y = y (x (t))$ ) na forma paramétrica, em que o parâmetro é time. Para construir a órbita desejada usando Python, definimos os raios das órbitas e os períodos de rotação da Terra e da Lua.

A Terra se move em um sistema de coordenadas heliocêntricas ( $$$K$ ) seu raio de órbita e o período de revolução são respectivamente iguais $$$R_ {1} = 1.496 \ cdot 10 ^ {8} km, T_ {1} = 3.156 \ cdot 10 ^ {7} s$ A lua se move ao redor da terra em um sistema de coordenadas ( $$$K ^ {'}$ ) seu raio de órbita e o período de revolução são respectivamente iguais $$$R_ {2} = 3,844 \ cdot 10 ^ {5} km, T_ {2} = 2,36 \ cdot 10 ^ {6} s$ .

Em vista de (4), determinamos as funções da dependência das coordenadas no tempo:

$$

$$\ binom {(X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} \ cdot t), Y (t) = R_ {1} \ cdot sin (\ frac {2 \ pi} {T_ {1}} \ cdot t)} {x (t) = R_ {2} \ cdot cos (\ frac {2 \ pi} {T_ {2}} \ cdot t), y (t) = R_ {2} \ cdot sin (\ frac {2 \ pi} {T_ {2}} \ cdot t)}, (5)$$

Usando (5), obtemos um par de coordenadas para a órbita da lua:

$$

$$\ binom {X_ {g} (t) = X (t) + x (t)} {Y_ {g} (t) = Y (t) + y (t)}, (6)$$

Definimos o número de pontos nos quais as coordenadas N = 1000 e o tempo discreto no intervalo do período de rotação da Terra são calculados $$$dt = \ frac {T_ {1}} {N}$ . Escreveremos um programa e construiremos um gráfico para a área de mudança de coordenadas positiva:


Temos:


Fig. 1

O cronograma criado permite expandir a tarefa de treinamento e ver qual será a órbita da lua se o raio da órbita da lua for $$$R_ {2} = 3,844 \ cdot 10 ^ {7}$ . . É claro para o leitor que nem sequer tem conhecimento especial em astronomia que a Lua não pode ter uma órbita assim em campos não-gravitacionais da Terra, e um raio hipotético é usado para estudar as condições para o aparecimento de loops . Faremos as alterações apropriadas no programa:


Temos:


Fig.2

Comparando as órbitas da lua mostradas na Fig. 1 e 2, encontramos suas diferenças significativas. Para explicar as razões dessas diferenças, é necessário comparar as velocidades lineares da lua no primeiro e segundo casos e a velocidade linear da Terra.

Como a direção da velocidade linear da Terra em relação ao Sol, bem como a direção da velocidade linear da Lua em relação à Terra, muda no tempo e a velocidade permanece constante em magnitude.

Como característica quantitativa da razão das velocidades lineares da lua e da terra no sistema de coordenadas heliocêntricas, deve-se escolher a diferença entre o módulo de velocidade linear da terra e a projeção da velocidade linear da lua na direção do vetor de velocidade linear da terra:

$$

$$v_ {o} (t) = \ esquerda | \ vec {V} (t) \ direita | - \ frac {(\ vec {V} (t) \ cdot \ vec {v} (t))} {\ left | \ vec {V} (t) \ right |}, (7)$$

Definimos as funções que descrevem as leis da mudança dos componentes da velocidade da Terra e da Lua:

$$

$$\ begin {matriz} V_ {x} (t) = \ frac {d} {dt} X (t), V_ {y} (t) = \ frac {d} {dt} Y (t) & \\ vx (t) = \ frac {d} {dt} x (t), vy (t) = \ frac {d} {dt} y (t) \ end {matrix}, (8)$$

Para determinar a velocidade resultante, levando em consideração a projeção, usamos a relação:

$$$D (t) = \ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} - \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}} \ cdot \ frac {V_ {x} (t) \ cdot vx (t) + V_ {y} (t) \ cdot vy (t)} {\ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} \ cdot \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}}}, (9)$

Escreveremos um programa levando em consideração (5), (8), (9) e o raio da órbita da lua $$$R_ {2} = 3,844 \ cdot 10 ^ {5}$ km:


Temos:


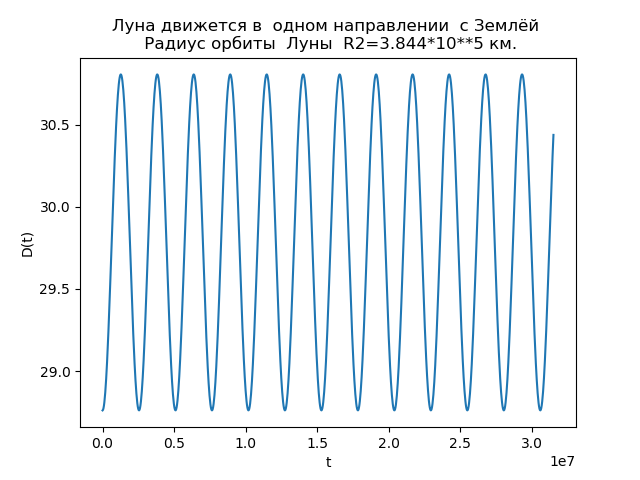Fig. 3.

Escreveremos um programa levando em consideração (5), (8), (9) e o raio da órbita da Lua R2 = 3,844 * 10 ** 7 km:


Temos:


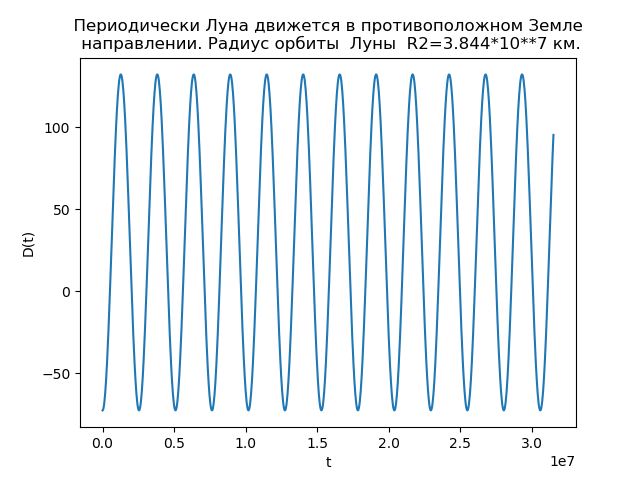Fig. 4.

A análise de dependências nos permite explicar o motivo das diferenças nas órbitas. A função D (t) para $$$R_ {2} = 3,844 \ cdot 10 ^ {5}$ km é sempre positivo, ou seja, a lua sempre se move na direção do movimento da Terra e não se formam laços. At $$$R_ {2} = 3,844 \ cdot 10 ^ {7}$ valor em km $$$D (t)$ assume valores negativos, e há momentos em que a lua se move na direção oposta à direção do movimento da Terra e, portanto, a órbita tem laços. Este era o significado de usar a órbita inexistente da lua nos cálculos.

Construção da órbita de Marte no quadro de referência associado à Terra

.


No sistema de referência heliocêntrico (sistema K), a Terra se move em um círculo de raio $$$R_ {1} = 1.496 \ cdot 10 ^ {8}$ km, período de circulação $$$T_ {1} = $ 365,2$ dia, Marte se move ao longo de uma elipse, cujo eixo semi-principal $$$am = 2,28 \ cdot 10 ^ {8}$ km, o período da revolução de Marte $$$T_ {m} = $ 689,9$ dias., a excentricidade da órbita $$$e = $ 0,09$ [3] O movimento da Terra é descrito pelo vetor de raio R (t) definido pela expressão (3). Devido ao fato de a órbita de Marte ser uma elipse, dependências $$$x = x (t), y = y (t)$ desde o tempo são configurados parametricamente [4]:

$$$x (\ varepsilon) = a_ {m} \ cdot (cos (\ varepsilon) -e)$ (10)

$$$y (\ varepsilon) = a_ {m} \ cdot \ sqrt {1-e ^ {2}} \ cdot sin (\ varepsilon)$ (11)

$$$t (\ varepsilon) = \ frac {T_ {m}} {2 \ pi} \ cdot (\ varepsilon-e \ cdot sin (\ varepsilon))$ (12)

Uma revolução completa da elipse corresponde a uma alteração no parâmetro <img $$$\ varepsilon$ de 0 a $$$2 \ pi$ . Para construir a órbita de Marte, é necessário calcular as coordenadas dos vetores de raio nos mesmos momentos que descrevem a posição da Terra e de Marte no referencial heliocêntrico e, em seguida, de acordo com a relação $$$\ vec {r ^ {'}} (t) = \ vec {r} (t) - \ vec {R} (t)$ calcular as coordenadas de Marte no quadro de referência associado à Terra.

Para construir a órbita de Marte no quadro de referência conectado à Terra, usamos os parâmetros anteriormente fornecidos das órbitas da Terra e Marte, relações (10) - (12) e também as relações para as coordenadas da Terra:

$$$X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} t)$ (13)

$$$Y (t) = R_ {1} \ cdot sin (\ frac {2 \ pi} {T_ {1}} t)$ (14)

Deve-se notar que o número de períodos de revolução de Marte ao redor do Sol é $$$K = 9$ , o número de pontos nos quais o cálculo deve ser feito e a distância entre eles será determinada a partir das relações:

$$$N = 4000 \ cdot K, \ varepsilon_ {i} = \ frac {2 \ pi} {N} \ cdot i, i = 0 ... N$ (15)


Temos:


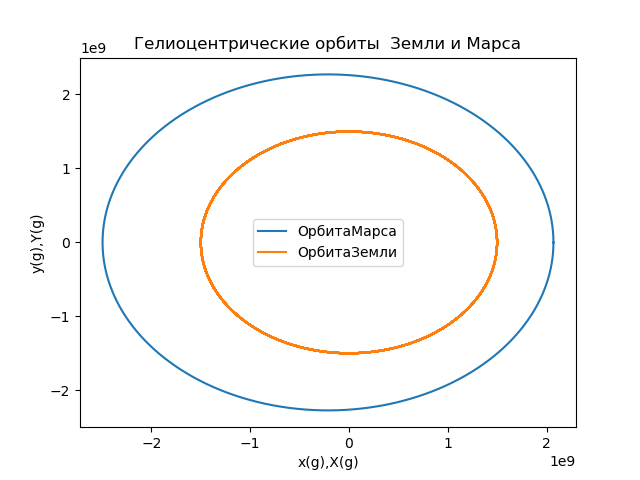Fig.5

Calculamos as coordenadas do vetor de raio que descrevem a posição de Marte no referencial conectado à Terra e construímos as órbitas (Fig. 6) usando a relação:

$$$x1_ {i} = x (\ varepsilon_ {i}) - X (t (\ varepsilon_ {i})), y1_ {i} = y (\ varepsilon_ {i}) - Y (t (\ varepsilon_ {i} ))$ (16)


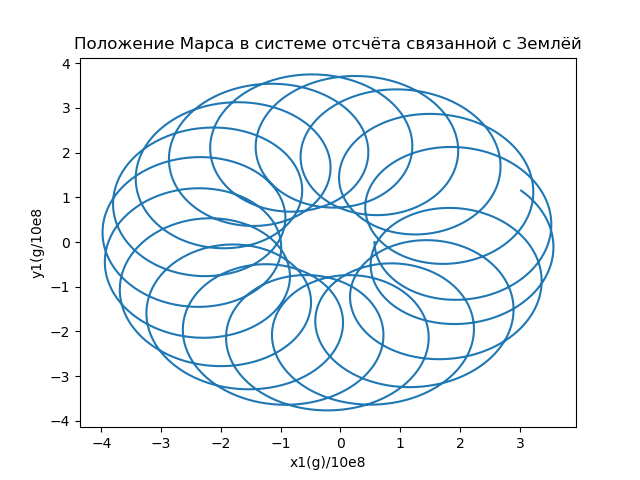Fig.6

Outra característica importante do movimento de Marte (principalmente para vôos espaciais interplanetários) é a distância entre a Terra e Marte s (t), que é determinada pelo módulo do vetor de raio que descreve a posição de Marte no quadro de referência associado à Terra. A dependência da distância entre a Terra e Marte do tempo medido em anos terrestres é apresentada na Fig. 7.


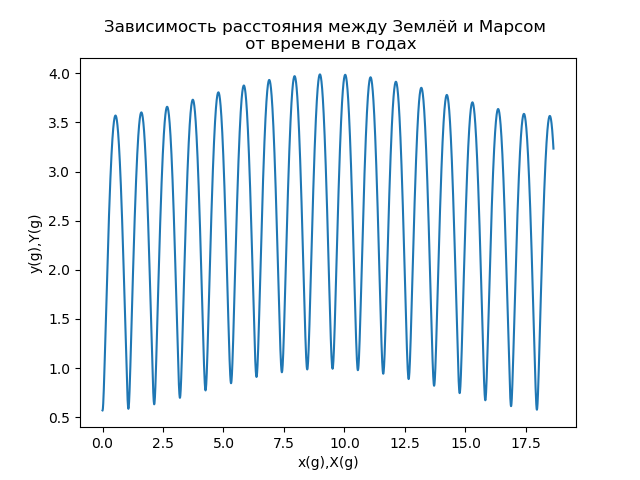Fig. 7

Uma análise da dependência mostrada na Fig. 7 mostra que a distância entre a Terra e Marte é uma função periódica complexa do tempo. Se usarmos a terminologia da teoria dos sinais [5], podemos dizer sobre a dependência s (t) que é um sinal modulado em amplitude, que geralmente é representado como o produto de duas funções de uma função de alta frequência (portadora) e baixa frequência que define a modulação de amplitude (envelope) :

$$$u (t) = (\ bar {u} + a \ cdot sin (\ omega_ {1} t)) \ cdot (1+ \ Delta a \ cdot sin (\ omega_ {2} t))$ (17)

onde $$$\ bar {u}$ - componente constante da função $$$u (t)$ ; $$$a$ - amplitude do sinal; $$$\ omega_ {1}$ - frequência portadora; $$$\ Delta a$ - a amplitude da função que define a profundidade da modulação de amplitude; $$$\ omega_ {2}$ - frequência da função de modulação.

A partir da Fig. 7, pode-se observar que o período da transportadora é de aproximadamente 2 anos, o período da função de modulação é de aproximadamente 17 anos] 6].

Construção da órbita heliocêntrica do cometa Halley

A última vez que o cometa Halley passou por seu periélio (o ponto de órbita mais próximo do Sol) em 9 de fevereiro de 1986. (O próprio Sol é considerado localizado na origem.)

As coordenadas e componentes de velocidade do cometa Halley naquele momento eram iguais $$$p_ {0} = (0,325514, 0,459460, 0,166229)$ e $$$v_ {0} = (–9.096111, –6.916686, –1.305721)$ respectivamente, e a distância aqui é expressa em unidades astronômicas de comprimento - a.u.d., ou simplesmente a.u. (unidade astronômica, ou seja, o comprimento da maior semiaxe principal da órbita da Terra) e o tempo em anos. Nestas unidades de medida, as equações tridimensionais de movimento do cometa têm a forma

$$

$$\ left \ {\ begin {matrix} \ frac {d ^ {2} x} {dt ^ {2}} = - \ frac {\ mu \ cdot x} {r ^ {3}} \\ \ frac { d ^ {2} y} {dt ^ {2}} = - \ frac {\ mu \ cdot y} {r ^ {3}} \\ \ frac {d ^ {2} z} {dt ^ {2} } = - \ frac {\ mu \ cdot z} {r ^ {3}} \ end {matrix} \ right., (18)$$

(18)

onde: $$$\ mu = 4 \ pi ^ {2}, r = \ sqrt {x ^ {2} + y ^ {2} + z ^ {2}}$


Temos:









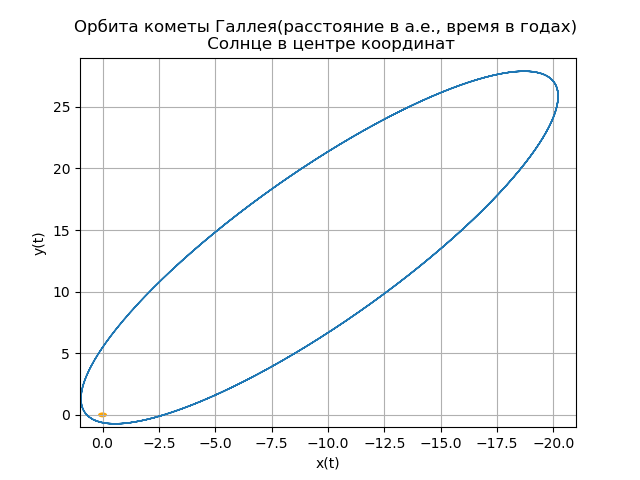
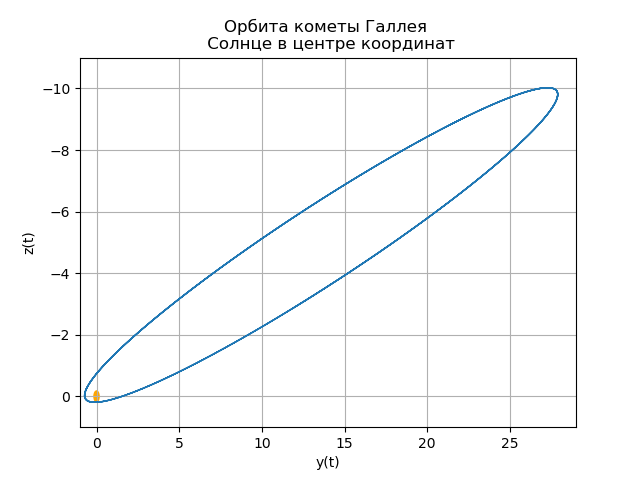
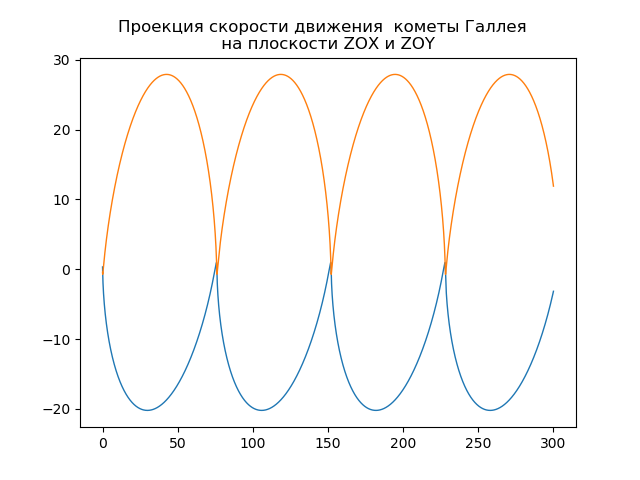Seu próprio cometa

Tente um experimento. À noite, você monta seu telescópio no topo de uma colina não muito longe de sua casa. A noite deve estar clara, sem nuvens, estrelada e, se a sorte lhe sorriu: às 0:30 da manhã, você notará um novo cometa.

Após repetidas observações nas noites seguintes, você poderá calcular suas coordenadas na primeira noite. Coordenadas no sistema de coordenadas heliocêntricas: P0 = (x0, y0, z0) e o vetor de velocidade v0 = (vx0, vy0, vz0).

Usando esses dados, determine:

• a distância do cometa do Sol no periélio (o ponto de órbita mais próximo do Sol) e no afélio (o ponto de órbita mais distante do Sol);
• velocidade do cometa ao passar pelo periélio e pelo afélio;
• o período de revolução do cometa em torno do sol;
• Nas próximas duas datas, o cometa passa pelo periélio.

Se medirmos a distância em unidades astronômicas e o tempo em anos, a equação de movimento do cometa assumirá a forma (18). Para o seu próprio cometa, selecione coordenadas de partida arbitrárias e velocidades da mesma ordem que o cometa de Halley.

Se necessário, refaça uma escolha arbitrária da posição inicial e do vetor de velocidade até obter uma órbita excêntrica plausível que vá além da órbita da Terra (como a maioria dos cometas reais).

Referências:

1. Feynman R., Leighton R., Sands M. Feynman Palestras em Física. 3rd ed. T. 1,2. M .: Mir, 1977.
2. Matveev A.N. Mecânica e Teoria da Relatividade. M.: Mais alto. escola., 1986.
3. Enciclopédia Física. T. 3. M.: Big Russian Encyclopedia, 1992.
4. Landau L.D., Lifshits E.M. Curso em Física Teórica. A mecânica M.: Fu-matgiz, 1958.
5. Baskakov S.I. Circuitos e sinais de engenharia de rádio. M.: Mais alto. escola., 1988.
6. Porshnev C.V. Simulação computacional de processos físicos usando o pacote mathcad .