Como nós da 1C: Enterprise resolvemos sistemas de equações algébricas

Trabalhar com matrizes numéricas em geral e resolver sistemas de equações algébricas lineares, em particular, é um problema matemático e algorítmico clássico que é amplamente usado na modelagem e cálculo de uma enorme classe de processos de negócios (por exemplo, no cálculo de custos). Ao criar e operar as configurações 1C: Enterprise, muitos desenvolvedores foram confrontados com a necessidade de implementar manualmente os algoritmos de cálculo de SLAU e, em seguida, com o problema de uma longa espera por uma solução.

“1C: Enterprise” 8.3.14 conterá funcionalidades que podem reduzir significativamente o tempo necessário para resolver sistemas de equações lineares usando um algoritmo baseado na teoria dos grafos.

É otimizado para uso em dados com uma estrutura esparsa (ou seja, contendo no máximo 10% de coeficientes diferentes de zero nas equações) e, em média e nos melhores casos, demonstra os assintóticos (n⋅log (n) log (n)), onde n é o número de variáveis ​​e, no pior caso (quando o sistema está cheio ~ 100%), seu comportamento assintótico é comparável aos algoritmos clássicos (Θ (n ³ )). Além disso, em sistemas com ~ 10 ⁵ incógnitas, o algoritmo mostra aceleração centenas de vezes em comparação com os implementados em bibliotecas especializadas de álgebra linear (por exemplo, superlu ou lapack ).


Importante: o artigo e o algoritmo descrito requerem uma compreensão da álgebra linear e da teoria dos grafos no nível do primeiro ano de uma universidade.

Apresentação do SLAE como um gráfico

Considere o sistema esparso mais simples de equações lineares:


Atenção: o sistema é gerado aleatoriamente e será usado posteriormente para demonstrar as etapas do algoritmo

À primeira vista, surge uma associação com outro objeto matemático - a matriz de adjacência do gráfico. Então, por que não converter os dados em listas de adjacência, economizando RAM em tempo de execução e acelerando o acesso a coeficientes diferentes de zero?

Para fazer isso, basta transpor a matriz e estabelecer a invariante “A [i] [j] = z ⇔ a i-ésima variável entra na j-ésima equação com o coeficiente z” e, em seguida, para qualquer A diferente de zero constrói a aresta correspondente do vértice i ao vértice j.

O gráfico resultante ficará assim:



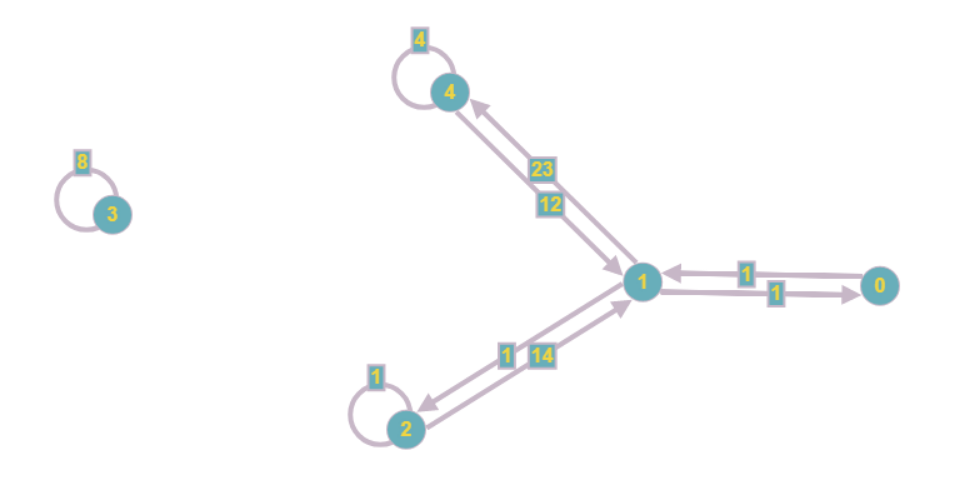
Mesmo visualmente, acaba sendo menos complicado, e os custos de memória assintótica diminuem de O (n ² ) para O (n + m), onde m é o número de coeficientes no sistema.

Isolamento de componentes fracamente conectados

A segunda idéia algorítmica que vem à mente quando se considera a entidade resultante: o uso do princípio de “dividir e conquistar”. Em termos de gráfico, isso leva à separação do conjunto de vértices em componentes fracamente conectados.

Deixe-me lembrá-lo de que o componente fracamente conectado é um subconjunto de vértices com inclusão máxima que, entre dois, existe um caminho a partir das arestas em um gráfico não direcionado. Podemos obter um gráfico não direcionado do original, por exemplo, adicionando o oposto a cada aresta (com remoção subsequente). Então, um vértice da conexão incluirá todos os vértices que podemos alcançar quando percorrermos o gráfico em profundidade.

Após a separação dos componentes fracamente conectados, o gráfico assumirá a seguinte forma:



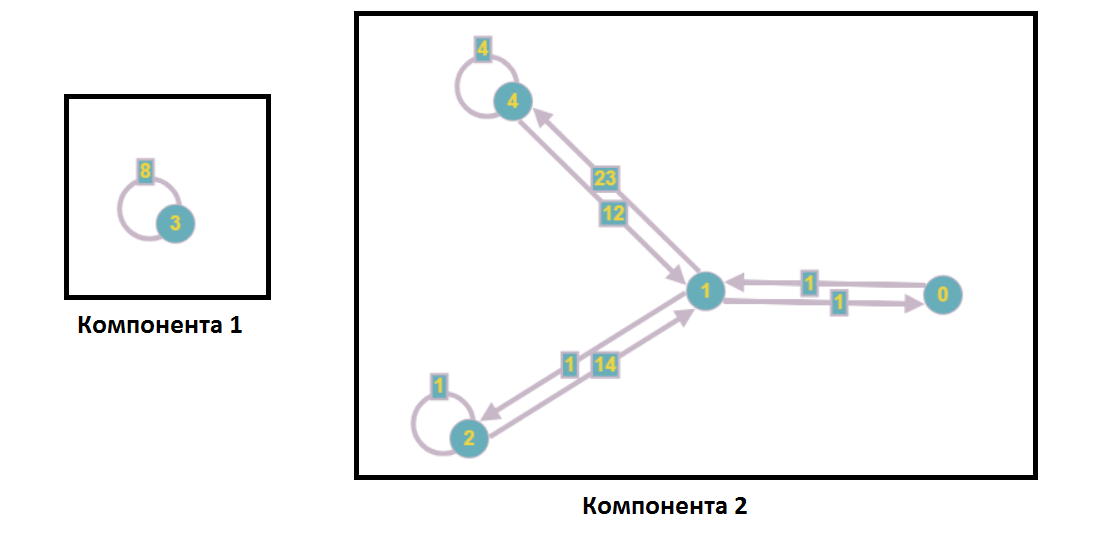
Como parte da análise de um sistema de equações lineares, isso significa que nenhum vértice do primeiro componente é incluído nas equações com os números do segundo componente e vice-versa, ou seja, podemos resolver esses subsistemas de forma independente (por exemplo, em paralelo).

Redução de vértice do gráfico

O próximo passo do algoritmo é exatamente o que é a otimização para trabalhar com matrizes esparsas. Mesmo no gráfico do exemplo, existem picos "suspensos", o que significa que algumas das equações incluem apenas um desconhecido e, como sabemos, o valor desse desconhecido é fácil de encontrar.

Para determinar tais equações, propõe-se armazenar uma matriz de listas contendo os números de variáveis ​​incluídas na equação com o número desse elemento da matriz. Então, quando a lista atingir o tamanho da unidade, podemos reduzir o vértice "único" e informar o restante das equações nas outras equações nas quais esse vértice entra.

Assim, podemos reduzir o vértice 3 do exemplo imediatamente após o processamento completo do componente:

$$

$$8⋅_3 = 4⇒_3 = 1/2$$

Da mesma forma, procedemos com a equação 0, pois ela contém apenas uma variável:

$$

$$1⋅x_1 = 1⇒x_1 = 1$$

Outras equações também serão alteradas após encontrar este resultado:

$$$$ display $$ 1⋅_1 ​​+ 1⋅_2 = 3⇒1⋅_2 = 3-1 = 2 $$ display $$

O gráfico tem o seguinte formato:



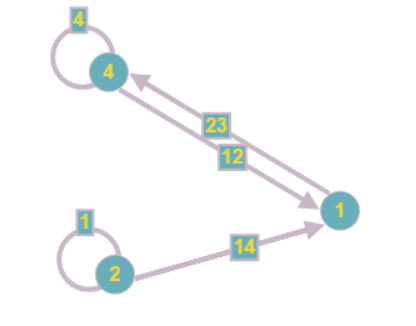
Observe que, ao reduzir um vértice, também podem aparecer outros que também contêm um desconhecido. Portanto, essa etapa do algoritmo deve ser repetida até que pelo menos um dos vértices possa ser reduzido.

Reconstrução de gráfico

Os leitores mais atentos podem perceber que é possível uma situação em que cada um dos vértices do gráfico tenha um grau de ocorrência de pelo menos dois e será impossível continuar a reduzir consistentemente os vértices.

O exemplo mais simples desse gráfico: cada vértice tem um grau de ocorrência igual a dois, nenhum dos vértices pode ser reduzido.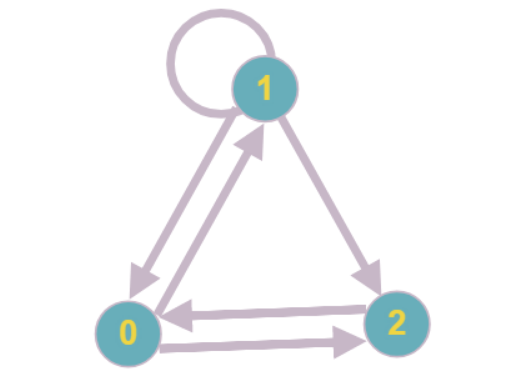



Como parte da otimização para matrizes esparsas, supõe-se que esses subgráficos sejam pequenos em tamanho; no entanto, você ainda precisará trabalhar com eles. Para calcular os valores das incógnitas que fazem parte do subsistema de equações, propõe-se o uso de métodos clássicos para resolver SLAEs (é por isso que a introdução indica que, para uma matriz na qual todos ou quase todos os coeficientes nas equações são diferentes de zero, nosso algoritmo terá a mesma complexidade assintótica dos padrões. )

Por exemplo, você pode trazer o conjunto de vértices restantes após a redução de volta para a forma matricial e aplicar o método Gauss para resolver SLAEs nele . Assim, obteremos a solução exata e a velocidade do algoritmo será reduzida devido ao processamento não de todo o sistema, mas apenas de parte dele.

Teste de algoritmo

Para testar a implementação do software do algoritmo, adotamos vários sistemas reais de equações de grande volume, bem como um grande número de sistemas gerados aleatoriamente.
A geração de um sistema aleatório de equações passou pela adição seqüencial de arestas de peso arbitrário entre dois vértices aleatórios. No total, o sistema estava 5-10% cheio. A correção das soluções foi verificada substituindo as respostas obtidas no sistema original de equações.


Os sistemas variaram de 1.000 a 200.000 incógnitas

Para comparar o desempenho, usamos as bibliotecas mais populares para resolver problemas de álgebra linear, como superlu e lapack. Obviamente, essas bibliotecas estão focadas em resolver uma ampla classe de problemas e a solução do SLAE neles não é otimizada de forma alguma, portanto a diferença de velocidade acabou sendo significativa.


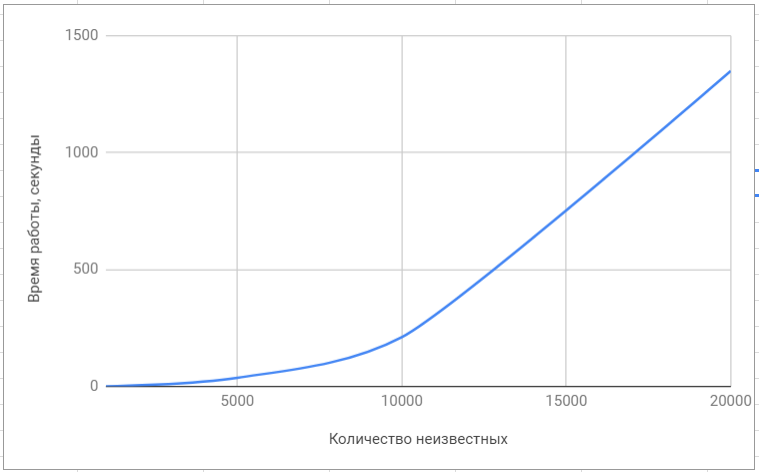Testando a biblioteca lapack


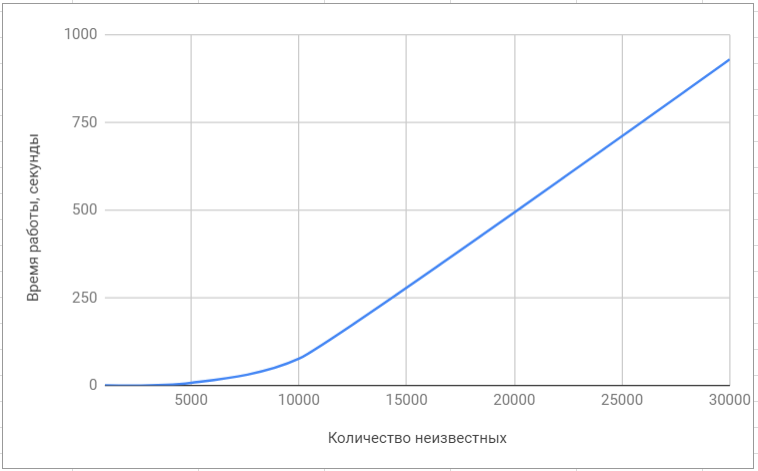Testando a biblioteca 'superlu'

Aqui está a comparação final do nosso algoritmo com os algoritmos implementados em bibliotecas populares:

Conclusão

Mesmo que você não seja um desenvolvedor de configuração 1C: Enterprise, as idéias e os métodos de otimização descritos neste artigo podem ser usados ​​por você não apenas na implementação de um algoritmo para resolver SLAEs, mas também para toda uma classe de problemas de álgebra linear relacionados a matrizes.

Para os desenvolvedores da 1C, acrescentamos que a nova funcionalidade da solução SLAE suporta o uso paralelo de recursos de computação, e você pode ajustar o número de threads de cálculo usados.