Richard Hamming: Capítulo 20. Modelagem - III

"O objetivo deste curso é prepará-lo para o seu futuro técnico."

Resta publicar dois capítulos ...

Modelagem - III

Continuarei a orientação geral dada no capítulo anterior, mas desta vez vou me concentrar na antiga expressão “Garbage in - garbage out”, que costuma ser abreviada como GIGO (garbage in, garbage out). A idéia é que, se você colocar dados coletados incorretamente e expressões definidas incorretamente na entrada, a saída poderá obter apenas resultados incorretos. O oposto também é assumido implicitamente: a partir da disponibilidade de dados de entrada precisos, o resultado correto é obtido. Mostrarei que essas duas suposições podem ser falsas.

Geralmente, a modelagem é baseada na resolução de equações diferenciais, portanto, para iniciantes, consideraremos a equação diferencial mais simples da primeira ordem da forma



Como você se lembra, o campo de direção são as linhas construídas em cada ponto do plano xy, com os coeficientes angulares dados pela equação diferencial (Figura 20.I). Por exemplo, uma equação diferencial possui um campo de direção mostrado na Figura 20.II.





Figura 20.I

Para cada círculo concêntrico,



de modo que a inclinação da reta seja sempre a mesma e dependa do valor de k. Tais curvas são chamadas isoclinas .

Agora, vejamos o campo de direção de outra equação diferencial (Figura 20.III). No lado esquerdo, vemos um campo de direções divergente, o que significa que pequenas alterações nos valores iniciais ou pequenos erros de cálculo levarão a uma grande diferença nos valores no meio do caminho. No lado direito, vemos que o campo de direção está convergindo. Isso significa que, com uma diferença maior no meio do caminho, a diferença de valores na extremidade direita será pequena. Este exemplo simples mostra como pequenos erros podem se tornar grandes, grandes erros pequenos e, além disso, como pequenos erros podem se tornar grandes e depois pequenos novamente. Portanto, a precisão da solução depende do intervalo específico no qual a solução é calculada. Não há precisão geral absoluta.



Figura 20.II



Figura 20.III

Essas considerações são construídas para a função


que é uma solução para a equação diferencial



Você provavelmente imaginou um "tubo" que primeiro se expande e depois se estreita em torno da "solução exata e verdadeira" da equação. Essa representação é perfeita para o caso de duas medições, mas quando eu tenho um sistema de n tais equações diferenciais - 28 no caso do problema de míssil interceptador para a Marinha mencionado anteriormente -, então esses "tubos" em torno da verdadeira solução da equação acabam não sendo o que parecem à primeira vista. Uma figura que consiste em quatro círculos em duas dimensões leva ao paradoxo de n-dimensões para o espaço dez-dimensional descrito no Capítulo 9. Essa é apenas outra visão do problema da modelagem estável e instável, descrita no capítulo anterior. Desta vez, darei exemplos específicos relacionados a equações diferenciais.

Como resolvemos equações diferenciais numericamente? Começando com a equação diferencial usual de primeira ordem, traçamos um campo de direções. Nossa tarefa é fazer com que um determinado valor inicial calcule o valor no próximo ponto de interesse mais próximo de nós. Se tomarmos o coeficiente de inclinação local da linha dada pela equação diferencial e dermos um pequeno passo adiante ao longo da tangente, introduziremos apenas um pequeno erro (Figura 20.IV).

Usando esse novo ponto, passaremos para o próximo ponto, mas, como pode ser visto na figura, gradualmente nos desviaremos da curva verdadeira, porque usamos o coeficiente de inclinação da etapa anterior e não o coeficiente de inclinação real para o intervalo atual. Para evitar esse efeito, "predizemos" um determinado valor, depois o usamos para estimar o coeficiente angular nesse ponto (usando a equação diferencial) e, em seguida, usamos o valor médio do coeficiente angular nos dois limites do intervalo como o coeficiente angular para esse intervalo.

Então, usando essa inclinação média, damos um passo adiante, desta vez usando a fórmula de “correção”. Se os valores obtidos usando as fórmulas “previsão” e “correção” forem próximos o suficiente, assumimos que nossos cálculos são precisos o suficiente, caso contrário, devemos reduzir o tamanho da etapa. Se a diferença entre os valores for muito pequena, devemos aumentar o tamanho da etapa. Assim, o esquema tradicional de previsão e correção possui um mecanismo interno para verificar erros em cada etapa, mas esse erro em uma etapa específica não é de forma alguma e em nenhum sentido um erro acumulado comum! É absolutamente claro que o erro acumulado depende se o campo de direção converge ou diverge.



Figura 20.IV



Figura 20.V

Usamos linhas retas simples para a etapa de previsão e a etapa de correção. O uso de polinômios de graus mais altos fornece um resultado mais preciso; polinômios de quarto grau são geralmente usados ​​(a solução de equações diferenciais pelo método de Adams-Bashfort, método de Milne, método de Hamming, etc.). Assim, devemos usar os valores da função e suas derivadas em vários pontos anteriores para prever o valor da função no próximo ponto, após o qual usamos a substituição desse valor na equação diferencial e aproximamos o novo valor do coeficiente angular. Usando os valores novos e anteriores do coeficiente angular, bem como os valores da função desejada, corrigimos o valor obtido. É hora de notar que o corretor nada mais é do que um filtro recursivo digital no qual os valores de entrada são derivados e os valores de saída são os valores da função desejada.

A estabilidade e outros conceitos discutidos anteriormente permanecem relevantes. Como mencionado anteriormente, há um loop de feedback adicional para a solução prevista da equação diferencial, que por sua vez é usada no cálculo do coeficiente angular ajustado. Ambos os valores são usados ​​na solução da equação diferencial, os filtros digitais recursivos são apenas fórmulas e nada mais. No entanto, eles não são características de transferência, pois são comumente considerados na teoria dos filtros digitais. Nesse caso, o cálculo dos valores da equação diferencial ocorre simplesmente. Nesse caso, a diferença entre as abordagens é significativa: nos filtros digitais, o sinal é processado linearmente, enquanto na resolução de equações diferenciais há não linearidade, que é introduzida pelo cálculo dos valores das derivadas da função. Isso não é o mesmo que um filtro digital.

Se você resolver um sistema de n equações diferenciais, estará lidando com um vetor de n componentes. Você prevê o próximo valor de cada componente, avalia cada uma das n derivadas, ajusta cada um dos valores previstos e aceita o resultado do cálculo nesta etapa ou o rejeita se o erro local for muito grande. Você tende a pensar em pequenos erros como um "tubo" em torno de um caminho calculado real. E novamente, peço que se lembre do paradoxo dos quatro círculos em espaços de alta dimensão. Esses "canos" podem não ser o que parecem à primeira vista.

Agora, deixe-me apontar a diferença significativa entre as duas abordagens: métodos computacionais e a teoria dos filtros digitais. Em livros didáticos comuns, apenas métodos de matemática computacional são descritos que aproximam funções por polinômios. Filtros recursivos usam frequências em fórmulas de avaliação! Isso leva a diferenças significativas!

Para ver a diferença, vamos imaginar que estamos desenvolvendo um simulador de um pouso humano em Marte. A abordagem clássica concentra-se na forma da trajetória de pouso e usa a aproximação polinomial para regiões locais. O caminho resultante terá pontos de interrupção na aceleração, conforme avançamos passo a passo de um intervalo para outro. No caso da abordagem de frequência, focaremos em obter as frequências corretas e deixar a localização como ela é. No caso ideal, ambas as trajetórias serão as mesmas, mas na prática elas podem diferir significativamente.

Qual caminhada devo usar? Quanto mais você pensa sobre isso, mais estará inclinado a acreditar que o piloto no simulador deseja ter uma "noção" do comportamento do módulo de aterrissagem, e parece que a resposta de frequência do simulador deve ser bem "sentida" pelo piloto. Se a localização for um pouco diferente, o loop de feedback compensará esse desvio durante o processo de pouso, mas se a "sensação" do controle diferir durante o voo real, o piloto ficará preocupado com novas "sensações" que não estavam no simulador. Sempre me pareceu que os simuladores deveriam preparar os pilotos para sensações reais o máximo possível (é claro, não podemos simular baixa gravidade em Marte por um longo tempo), para que eles se sintam confortáveis ​​quando, na realidade, encontram uma situação com a qual encontrado repetidamente no simulador. Infelizmente, sabemos muito pouco sobre o que o piloto "sente". O piloto apenas sente as freqüências reais da expansão de Fourier, ou também as complexas frequências de Laplace que estão desaparecendo (ou talvez devamos usar wavelets?). Pilotos diferentes sentem as mesmas coisas? Precisamos saber mais do que sabemos agora sobre essas condições essenciais de design.

A situação descrita acima é uma contradição padrão entre a abordagem matemática e de engenharia para resolver o problema. Essas abordagens têm objetivos diferentes na solução de equações diferenciais (como no caso de muitos outros problemas), portanto, levam a resultados diferentes. Se você criar modelagem, verá que existem nuanças ocultas que se revelam muito importantes na prática, mas sobre as quais os matemáticos não sabem nada e, de todas as maneiras, negam as consequências de negligenciá-las. Vamos dar uma olhada em dois caminhos (Figura 20.IV), que eu calculei aproximadamente. A curva superior descreve com mais precisão a localização, mas as curvas dão uma "sensação" completamente diferente em comparação com o mundo real, a segunda curva é mais equivocada na localização, mas tem maior precisão em termos de "sensação". Novamente demonstrei claramente por que acredito que uma pessoa com um profundo entendimento da área de assunto do problema também deve entender os métodos matemáticos para resolvê-lo, e não confiar nos métodos tradicionais de solução.

Agora, quero contar outra história sobre os primeiros dias de teste do sistema de defesa antimísseis da Nike. Naquela época, estavam ocorrendo testes de campo em White Sands, também chamado de "teste de telefone de campo". Foram lançamentos de teste nos quais o foguete teve que seguir uma trajetória predeterminada e explodir no último momento, para que toda a energia da explosão não fosse além de um determinado território e causasse mais danos, o que era preferível a uma queda mais suave de partes individuais do foguete no solo, o que supostamente deveria ter causado menos danos. O objetivo dos testes foi obter medições reais de levantamento e arrasto em função da altitude e velocidade do vôo, a fim de depurar e melhorar o design.

Quando conheci meu amigo que havia retornado dos testes, ele vagou pelos corredores dos Laboratórios Bell e parecia bastante infeliz. Porque Porque os dois primeiros dos seis lançamentos programados falharam no meio do voo e ninguém sabia o porquê. Os dados necessários para as etapas adicionais do design não estavam disponíveis, o que significava sérios problemas para todo o projeto. Eu disse que, se ele pode me fornecer equações diferenciais que descrevam o vôo, posso colocar a garota para resolvê-las (obter acesso a computadores grandes no final da década de 1940 não foi fácil). Após cerca de uma semana, eles forneceram sete equações diferenciais de primeira ordem e a garota estava pronta para começar. Mas quais eram as condições iniciais um momento antes do início dos problemas em voo? (Naqueles dias, não tínhamos poder de computação suficiente para calcular rapidamente toda a trajetória de vôo.) Eles não sabiam! Os dados de telemetria eram incompreensíveis um momento antes da falha. Não fiquei surpreso e isso não me incomodou. Então, usamos os valores estimados de altitude, velocidade de vôo, ângulo de ataque etc. - uma condição inicial para cada uma das variáveis ​​que descrevem a trajetória de voo. Em outras palavras, eu tinha lixo na entrada. Mas, antes, percebi que a natureza dos testes de campo que simulamos era tal que pequenos desvios da trajetória proposta eram automaticamente corrigidos pelo sistema de orientação! Eu estava lidando com um campo de direções muito convergente.

Descobrimos que o foguete era estável ao longo dos eixos transversal e vertical, mas quando um deles se estabilizou, um excesso de energia levou a oscilações ao longo do outro eixo. Assim, houve não apenas oscilações ao longo dos eixos transversal e vertical, mas também uma transmissão periódica de energia crescente entre eles, causada pela rotação do foguete em torno de seu eixo longitudinal. Assim que as curvas calculadas para uma pequena parte da trajetória foram demonstradas, todos imediatamente perceberam que a estabilização cruzada não era levada em consideração e todos sabiam como corrigi-la. Portanto, obtivemos uma solução que também nos permitiu ler os dados de telemetria estragados obtidos durante os testes e esclarecer o período de transferência de energia - de fato, fornecer as equações diferenciais corretas para os cálculos. Tive um pouco de trabalho, exceto para me certificar de que a garota da calculadora de mesa calculasse honestamente tudo. Portanto, em maio, o mérito foi entender que (1) podemos simular o que aconteceu (agora é uma rotina na investigação de acidentes, mas depois foi uma inovação) e (2) o campo de direção converge, portanto as condições iniciais podem não ser especificadas exatamente.

Contei essa história para mostrar que o princípio GIGO nem sempre funciona. Uma história semelhante aconteceu comigo durante uma simulação inicial de bomba em Los Alamos. Gradualmente, cheguei a entender que nossos cálculos, construídos para a equação de estado, eram baseados em dados bastante imprecisos. A equação de estado relaciona a pressão e a densidade de uma substância (também temperatura, mas vou omitir neste exemplo). Dados de laboratórios de alta pressão, aproximações obtidas no estudo de terremotos, densidade de núcleo estelar e teoria assintótica de pressões infinitas foram representados como pontos em um gráfico muito grande (Figura 20.VII). Em seguida, usando padrões, desenhamos curvas que conectavam os pontos dispersos. Então, com base nessas curvas, construímos tabelas de valores de funções com uma precisão de 3 casas decimais. Isso significa que simplesmente assumimos 0 ou 5 na quarta casa decimal. Usamos esses dados para criar tabelas com as casas decimais 5 e 6. Com base nessas tabelas, nossos cálculos adicionais foram construídos. Naquela época, como eu já mencionei, eu era uma espécie de calculadora, e meu trabalho era contar e, assim, libertar físicos dessa ocupação, para permitir que eles fizessem seu trabalho.



Figura 20.VII

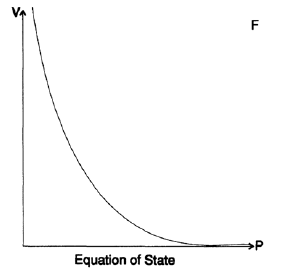
Depois que a guerra terminou, fiquei em Los Alamos por mais meio ano, e uma das razões pelas quais fiz isso foi porque eu queria entender como esses dados imprecisos poderiam levar a uma simulação tão precisa do design final. Pensei nisso por um longo tempo e encontrei a resposta. No meio dos cálculos, usamos diferenças finitas de segunda ordem. A diferença de primeira ordem mostrou o valor da força em um lado de cada concha, e as diferenças das conchas adjacentes em ambos os lados deram a força resultante, que move a concha. Fomos forçados a usar conchas finas, então subtraímos números muito próximos um do outro e precisávamos usar muitos dígitos após o ponto decimal. Estudos posteriores mostraram que, quando a "coisa" explodiu, a concha se moveu para cima ao longo da curva, e provavelmente às vezes parcialmente retrocedeu, de modo que qualquer erro local na equação de estado estava próximo do valor médio. Era realmente importante obter a curvatura da equação de estado e, como já observado, deveria ter sido precisa em média. Assim, lixo na entrada, mas mais preciso do que nunca, resulta em resultados!

Esses três exemplos mostram o que foi implicitamente mencionado anteriormente - se houver um loop de feedback para as variáveis ​​usadas no problema, não será necessário conhecer exatamente seus valores. Com base nisso, a notável idéia de G.S. Black de como construir um loop de feedback em amplificadores (Figura 20.VIII): enquanto o ganho for muito alto, apenas a resistência de um resistor deve ser correspondida com precisão, todas as outras partes podem ser implementado com baixa precisão. Para o circuito mostrado na Figura 20.VIII, obtemos as seguintes expressões:



Figura 20.VIII

Como você pode ver, quase toda a incerteza de medição está concentrada em um resistor com um valor nominal de 1/10, enquanto o coeficiente de transmissão pode ser impreciso. Portanto, o loop de feedback de Black nos permite construir coisas precisas a partir de peças imprecisas.



Agora você entende por que não posso lhe dar uma fórmula elegante, adequada para todas as ocasiões. Deve depender de quais cálculos são executados em quantidades específicas. Os valores imprecisos passarão por um loop de feedback que compensa o erro ou os erros sairão do sistema sem proteção de feedback? Se nenhum feedback for fornecido para as variáveis, é vital obter os valores exatos.
Portanto, a conscientização desse fato pode afetar o design do sistema! Um sistema bem projetado protege você de ter que usar um grande número de componentes de precisão. Mas tais princípios de design ainda são incompreendidos no momento e requerem estudo cuidadoso. E a questão não é que bons designers não entendam isso no nível da intuição; simplesmente não é tão fácil aplicar esses princípios nos métodos de design que você estudou. As mentes ainda precisam de todas as ferramentas de design automatizado que desenvolvemos. As melhores mentes serão capazes de integrar esses princípios nos métodos de design estudados para torná-los acessíveis "prontos para uso" para todos os outros.

Passemos agora a outro exemplo e princípio, que me permitiu obter uma solução para um problema importante. Foi-me dada uma equação diferencial



Percebe-se imediatamente que o valor da condição no infinito é realmente o lado direito da equação diferencial igual a zero, Figura 20.IX

Mas vejamos a questão da estabilidade. Se o valor de y em algum ponto suficientemente remoto x se tornar grande o suficiente, então o valor de sinh ( y ) se torna muito maior, a segunda derivada assume um grande valor positivo e a curva dispara para mais infinito. Da mesma forma, se ypequeno demais, a curva dispara em direção ao infinito negativo. E não importa se estamos movendo da esquerda para a direita ou da direita para a esquerda. Anteriormente, quando me deparei com um campo divergente de direções, usei o truque óbvio: integrei-me na direção oposta e obtive a solução exata. Mas, neste caso, é como se estivéssemos no topo de uma duna de areia e, assim que as duas pernas estiverem na mesma encosta, quebramos.



Figura 20.IX

Tentei usar a expansão em séries de potência, expansão em séries sem potência, aproximando-se da curva original, mas o problema não desapareceu, especialmente para grandes valores de k. Nem eu nem meus amigos conseguimos oferecer uma solução adequada. Depois fui aos diretores do problema e, em primeiro lugar, comecei a contestar a condição de contorno no infinito, no entanto, verificou-se que essa condição estava relacionada à distância medida nas camadas das moléculas e, naquele momento, qualquer transistor praticamente viável possuía um número quase infinito de camadas. Então comecei a disputar a equação, e eles novamente venceram a discussão, e tive que voltar ao meu escritório e continuar pensando.

Essa foi uma tarefa importante relacionada ao design e entendimento dos transistores que estavam sendo desenvolvidos naquele momento. Sempre argumentei que, se a tarefa é importante e colocada corretamente, posso encontrar alguma solução. Portanto, não tive escolha: era uma questão de honra.

Levei alguns dias de reflexão para perceber que a instabilidade era a chave para um método adequado. Eu construí a solução da equação diferencial em um pequeno intervalo usando o analisador diferencial que eu tinha na época e, se a solução disparou, significa que eu escolhi muito coeficiente angular, se derrubou, então eu escolhi também valor pequeno. Assim, com pequenos passos, caminhei ao longo da crista da duna e, assim que a decisão veio de um lado, eu sabia o que precisava ser feito para voltar à crista. Como você pode ver, o orgulho profissional é um bom auxiliar quando você precisa encontrar uma solução para uma tarefa importante em condições difíceis. Quão fácil foi recusar-se a resolver esse problema, referir-se ao fato de ser insolúvel,postei incorretamente ou encontrei outras desculpas, mas ainda acredito que tarefas importantes e colocadas corretamente permitem obter novas informações úteis. Vários problemas relacionados à carga espacial, que resolvi usando métodos computacionais, tinham uma complexidade semelhante associada à instabilidade em ambas as direções.

Antes de contar a história a seguir, quero lembrá-lo do teste de Rorschach, que foi popular durante a minha juventude. Uma gota de tinta é aplicada a uma folha de papel, após a qual é dobrada ao meio e, quando é desembrulhada novamente, é obtida uma mancha simétrica de forma bastante aleatória. A sequência desses borrões é mostrada aos indivíduos que são solicitados a dizer o que veem. Suas respostas são usadas para analisar as "características" de sua personalidade. Obviamente, as respostas são uma invenção de sua imaginação, pois essencialmente o local tem uma forma aleatória. É como olhar para as nuvens no céu e discutir como elas são. Você está discutindo apenas os frutos de sua imaginação, não a realidade, e isso, em certa medida, abre novas coisas sobre você, não sobre as nuvens. Sugiro que o método de mancha de tinta não seja mais usado.

E agora vamos à história em si. Uma vez, minha amiga psicóloga da Bella Laboratories construiu um carro no qual havia 12 interruptores e duas lâmpadas - vermelha e verde. Você define os interruptores, pressiona o botão e acende uma luz vermelha ou verde. Depois que o primeiro sujeito fez 20 tentativas, ele propôs uma teoria sobre como acender uma lâmpada verde. Essa teoria foi passada para a próxima vítima, após a qual ela também teve 20 tentativas para propor sua teoria sobre como acender uma lâmpada verde. E assim por diante ad infinitum. O objetivo do experimento foi estudar como as teorias se desenvolvem.

Mas meu amigo, agindo em seu próprio estilo, conectou as lâmpadas a uma fonte aleatória de sinais! Certa vez, ele reclamou que nem um único participante do experimento (e todos eles eram pesquisadores de primeira classe dos Laboratórios Bell) disse que não havia um padrão. Sugeri imediatamente que nenhum deles era especialista em estatística ou teoria da informação - são esses dois tipos de especialistas que estão familiarizados com eventos aleatórios. Um teste mostrou que eu estava certo!

Esta é uma conseqüência triste da sua educação. Você estudou com amor como uma teoria é substituída por outra, mas não estudou como abandonar uma bela teoria e aceitar o acaso. Era exatamente isso que era necessário: estar preparado para admitir que a teoria que acabamos de ler não é adequada e que não há regularidade nos dados, pura chance!

Eu tenho que insistir nisso com mais detalhes. Os estatísticos se perguntam constantemente: "O que eu quero dizer com verdade acontece ou é apenas um ruído aleatório?" Eles desenvolveram métodos de teste especiais para responder a essa pergunta. Suas respostas não são um sim ou não definitivo, mas sim ou não com um certo nível de confiança. Um limiar de confiança de 90% significa que geralmente em 10 tentativas, você se enganará apenas uma vez, desde que todas as outras hipóteses estejam corretas.Nesse caso, uma de duas coisas: você encontrou algo que não é (um erro do primeiro tipo) ou perdeu o que estava procurando (um erro do segundo tipo). São necessários muito mais dados para obter um nível de confiança de 95%, e a coleta de dados pode ser muito cara no momento. A coleta de dados adicionais também requer tempo adicional e a tomada de decisões é adiada - esse é o truque favorito das pessoas que não querem ser responsáveis ​​por suas decisões. "Precisa de mais informações", eles dirão a você.

Eu absolutamente afirmo seriamente que a maioria das simulações realizadas nada mais é do que um teste de Rorschach. Vou citar um destacado praticante da teoria do controle de Jay Forrester: “Do comportamento do sistema, surgem dúvidas que exigem uma revisão das premissas iniciais. A partir do processo de processamento das premissas iniciais sobre as partes e o comportamento observado do todo, aprimoramos nosso entendimento da estrutura e dinâmica do sistema. Este livro é o resultado de vários ciclos de re-estudo concluídos pelo autor. ”

Como um leigo pode distinguir isso do teste de Rorschach? Ele viu algo simplesmente porque queria vê-lo ou descobriu uma nova faceta da realidade? Infelizmente, muitas vezes a modelagem contém alguns ajustes que permitem "ver apenas o que você deseja". Esse é o caminho de menor resistência, e é por isso que a ciência clássica envolve um grande número de precauções, que atualmente são simplesmente ignoradas.

Você acha que é cuidadoso o suficiente para não ter ilusões? Vejamos o famoso estudo duplo-cego, que é uma prática comum na medicina. No início, os médicos descobriram que os pacientes notaram uma melhora quando pensaram que estavam recebendo um novo medicamento, enquanto os pacientes do grupo controle que sabiam que não estavam recebendo um novo medicamento não sentiram uma melhora. Depois disso, os médicos randomizaram os grupos e começaram a dar a alguns pacientes um placebo, para que não pudessem enganar os médicos. Mas, para seu horror, os médicos descobriram que os médicos que sabiam quem estava tomando o medicamento e quem não estava, também encontraram melhorias naqueles que esperavam e não encontraram melhorias naqueles que não esperavam.Como último recurso, os médicos começaram a adotar universalmente o método de estudo duplo-cego - até que todos os dados sejam coletados, nem os médicos nem os pacientes sabem quem está tomando o novo medicamento e quem não está. No final do experimento, os estatísticos abrem o envelope selado e analisam. Os médicos que procuraram a honestidade descobriram que eles próprios não eram. Você está fazendo a simulação tão melhor que pode ser confiável? Você tem certeza de que simplesmente não encontrou o que estava tão ansioso para encontrar? Auto-engano é muito comum.Você está fazendo a simulação tão melhor que pode ser confiável? Você tem certeza de que simplesmente não encontrou o que estava tão ansioso para encontrar? Auto-engano é muito comum.Você está fazendo a simulação tão melhor que pode ser confiável? Você tem certeza de que simplesmente não encontrou o que estava tão ansioso para encontrar? Auto-engano é muito comum.

Comecei o capítulo 19 fazendo a pergunta: por que todos deveriam acreditar na simulação feita? Agora, esse problema se tornou mais óbvio para você. Não é tão fácil responder a essa pergunta até que você tome muito mais medidas de precaução do que normalmente é tomado. Lembre-se também de que no seu futuro de alta tecnologia, provavelmente, você representará o lado do cliente da simulação e, com base nos resultados, terá que tomar decisões. Não há outras maneiras além da modelagem para obter a resposta para a pergunta "E se ...?". No capítulo 18, considerei decisões que deveriam ser tomadas, e não adiadas o tempo todo, se a organização não vasculhar e desviar sem parar - presumo que você estará entre aqueles que terão que tomar uma decisão.

A modelagem é necessária para responder à pergunta “E se ...?”, Mas, ao mesmo tempo, é cheia de armadilhas e você não deve confiar nos resultados simplesmente porque grandes recursos humanos e de hardware foram usados ​​para obter belas impressões coloridas ou curvas em um osciloscópio. Se você é quem toma a decisão final, toda a responsabilidade é sua. Decisões colegiais que levam a uma confusão de responsabilidades raramente são boas práticas - elas geralmente são um compromisso medíocre que carece dos méritos de qualquer um dos caminhos possíveis. A experiência me ensinou que um chefe decisivo é muito melhor do que um chefe tagarela. Nesse caso, você sabe exatamente onde está e pode continuar o trabalho que precisa ser feito.

A pergunta "E se ...?" frequentemente o confrontará no futuro, portanto, você precisa lidar com os recursos básicos e de modelagem para estar pronto para desafiar os resultados e entender os detalhes sempre que necessário.

Para continuar ...

Quem quer ajudar com a tradução, o layout e a publicação do livro - escreva em um e-mail pessoal ou envie um e-mail para magisterludi2016@yandex.ru

A propósito, também lançamos a tradução de outro livro interessante - “A Máquina dos Sonhos: A História da Revolução Computacional” )