
Acho que um pouco de absurdo na terça-feira não vai prejudicar a semana de trabalho. Eu tenho um hobby, no meu tempo livre, tento descobrir como invadir o algoritmo de mineração de bitcoin, evitar a busca estúpida de nonse e encontrar uma solução para o problema de correspondência de hash com consumo mínimo de energia. Devo dizer imediatamente o resultado, é claro, ainda não consegui, mas, no entanto, por que não expor por escrito as idéias que nascem na cabeça? Em algum lugar eles precisam ser colocados ...
Apesar da ilusão das idéias abaixo, acho que este artigo pode ser útil para alguém que está estudando
- Linguagem C ++ e seus modelos
- alguns circuitos digitais
- um pouco de teoria das probabilidades e aritmética probabilística
- algoritmo de hash bitcoin em detalhes
Por onde começamos?
Talvez do último e mais chato item desta lista? Paciência, então será mais divertido.
Vamos considerar em detalhes o algoritmo para calcular a função hash do bitcoin. É simples F (x) = sha256 (sha256 (x)), onde x é a entrada 80 bytes, o cabeçalho do bloco juntamente com o número da versão do bloco, hash do bloco anterior, raiz do merkle, carimbo de data e hora, bits e nonce. Aqui estão exemplos de cabeçalhos de bloco relativamente recentes que são passados para a função de hash:
Esse conjunto de bytes é um material bastante valioso, pois muitas vezes não é fácil para os mineradores entender em que ordem os bytes devem seguir ao formar o cabeçalho, invertendo frequentemente os locais de bytes altos e baixos (endianos).
Portanto, no cabeçalho do bloco, 80 bytes são considerados o hash sha256 e, a partir do resultado, outro sha256.
O próprio algoritmo sha256, se você olhar para diferentes fontes, geralmente consiste em quatro funções:
- vazio sha256_init (SHA256_CTX * ctx);
- void sha256_transform (SHA256_CTX * ctx, dados constantes do BYTE []);
- void sha256_update (SHA256_CTX * ctx, dados constantes do BYTE [], size_t len);
- void sha256_final (SHA256_CTX * ctx, hash BYTE []);
A primeira função chamada ao calcular o hash é sha256_init (), que restaura a estrutura SHA256_CTX. Não há nada de especial lá, exceto oito palavras de estado de 32 bits, que são inicialmente preenchidas com palavras especiais:
void sha256_init(SHA256_CTX *ctx) { ctx->datalen = 0; ctx->bitlen = 0; ctx->state[0] = 0x6a09e667; ctx->state[1] = 0xbb67ae85; ctx->state[2] = 0x3c6ef372; ctx->state[3] = 0xa54ff53a; ctx->state[4] = 0x510e527f; ctx->state[5] = 0x9b05688c; ctx->state[6] = 0x1f83d9ab; ctx->state[7] = 0x5be0cd19; }
Suponha que tenhamos um arquivo cujo hash precisa ser calculado. Lemos o arquivo com blocos de tamanho arbitrário e chamamos a função sha256_update () onde passamos o ponteiro para os dados do bloco e o comprimento do bloco. A função acumula o hash na estrutura SHA256_CTX na matriz de estados:
void sha256_update(SHA256_CTX *ctx, const BYTE data[], size_t len) { uint32_t i; for (i = 0; i < len; ++i) { ctx->data[ctx->datalen] = data[i]; ctx->datalen++; if (ctx->datalen == 64) { sha256_transform(ctx, ctx->data); ctx->bitlen += 512; ctx->datalen = 0; } } }
Por si só, sha256_update () chama a função de cavalo de trabalho sha256_transform (), que já aceita blocos de apenas um comprimento fixo de 64 bytes:
#define ROTLEFT(a,b) (((a) << (b)) | ((a) >> (32-(b)))) #define ROTRIGHT(a,b) (((a) >> (b)) | ((a) << (32-(b)))) #define CH(x,y,z) (((x) & (y)) ^ (~(x) & (z))) #define MAJ(x,y,z) (((x) & (y)) ^ ((x) & (z)) ^ ((y) & (z))) #define EP0(x) (ROTRIGHT(x,2) ^ ROTRIGHT(x,13) ^ ROTRIGHT(x,22)) #define EP1(x) (ROTRIGHT(x,6) ^ ROTRIGHT(x,11) ^ ROTRIGHT(x,25)) #define SIG0(x) (ROTRIGHT(x,7) ^ ROTRIGHT(x,18) ^ ((x) >> 3)) #define SIG1(x) (ROTRIGHT(x,17) ^ ROTRIGHT(x,19) ^ ((x) >> 10)) /**************************** VARIABLES *****************************/ static const uint32_t k[64] = { 0x428a2f98,0x71374491,0xb5c0fbcf,0xe9b5dba5,0x3956c25b,0x59f111f1,0x923f82a4,0xab1c5ed5, 0xd807aa98,0x12835b01,0x243185be,0x550c7dc3,0x72be5d74,0x80deb1fe,0x9bdc06a7,0xc19bf174, 0xe49b69c1,0xefbe4786,0x0fc19dc6,0x240ca1cc,0x2de92c6f,0x4a7484aa,0x5cb0a9dc,0x76f988da, 0x983e5152,0xa831c66d,0xb00327c8,0xbf597fc7,0xc6e00bf3,0xd5a79147,0x06ca6351,0x14292967, 0x27b70a85,0x2e1b2138,0x4d2c6dfc,0x53380d13,0x650a7354,0x766a0abb,0x81c2c92e,0x92722c85, 0xa2bfe8a1,0xa81a664b,0xc24b8b70,0xc76c51a3,0xd192e819,0xd6990624,0xf40e3585,0x106aa070, 0x19a4c116,0x1e376c08,0x2748774c,0x34b0bcb5,0x391c0cb3,0x4ed8aa4a,0x5b9cca4f,0x682e6ff3, 0x748f82ee,0x78a5636f,0x84c87814,0x8cc70208,0x90befffa,0xa4506ceb,0xbef9a3f7,0xc67178f2 }; /*********************** FUNCTION DEFINITIONS ***********************/ void sha256_transform(SHA256_CTX *ctx, const BYTE data[]) { uint32_t a, b, c, d, e, f, g, h, i, j, t1, t2, m[64]; for (i = 0, j = 0; i < 16; ++i, j += 4) m[i] = (data[j] << 24) | (data[j + 1] << 16) | (data[j + 2] << 8) | (data[j + 3]); for (; i < 64; ++i) m[i] = SIG1(m[i - 2]) + m[i - 7] + SIG0(m[i - 15]) + m[i - 16]; a = ctx->state[0]; b = ctx->state[1]; c = ctx->state[2]; d = ctx->state[3]; e = ctx->state[4]; f = ctx->state[5]; g = ctx->state[6]; h = ctx->state[7]; for (i = 0; i < 64; ++i) { t1 = h + EP1(e) + CH(e, f, g) + k[i] + m[i]; t2 = EP0(a) + MAJ(a, b, c); h = g; g = f; f = e; e = d + t1; d = c; c = b; b = a; a = t1 + t2; } ctx->state[0] += a; ctx->state[1] += b; ctx->state[2] += c; ctx->state[3] += d; ctx->state[4] += e; ctx->state[5] += f; ctx->state[6] += g; ctx->state[7] += h; }
Quando todo o arquivo hash tiver sido lido e já transferido para a função sha256_update (), resta apenas chamar a função sha256_final () final, que, se o tamanho do arquivo não for múltiplo de 64 bytes, ele adicionará bytes de preenchimento adicionais, escreverá o bytes de preenchimento adicionais, gravará o comprimento total dos dados no final do último bloco de dados e fará o sha256_transform () final.
O resultado do hash permanece na matriz de estados.
Este é o "alto nível", por assim dizer.
Em relação ao minerador de Bitcoin, é claro, os desenvolvedores pensam em considerar menor e mais eficiente.
É simples: o cabeçalho contém apenas 80 bytes, o que não é um múltiplo de 64 bytes. Portanto, seria necessário que o primeiro sha256 fizesse dois sha256_transform () já. No entanto, felizmente para os mineradores, o nonce do bloco está no final do cabeçalho, então o primeiro sha256_transform () pode ser executado apenas uma vez - este será o chamado meio-estado. Em seguida, o minerador passa por todas as opções não-nulas, que são 4 bilhões, 2 ^ 32 e as substitui no campo correspondente pela segunda sha256_transform (). Essa transformação conclui a primeira função sha256. Seu resultado são oito palavras de 32 bits, ou seja, 32 bytes. É fácil encontrar o sha256 a partir deles - o sha256_transform () final é chamado e tudo está pronto. Observe que os dados de entrada são 32 bytes menores que os 64 bytes necessários para sha256_transform (). Então, novamente, o bloco será preenchido com zeros e o comprimento do bloco será inserido no final.
No total, existem apenas três chamadas para sha256_transform (), das quais a primeira deve ser lida apenas uma vez para calcular o meio do estado.
Tentei expandir todas as manipulações de dados que ocorrem ao calcular o hash do cabeçalho de um bloco de bitcoin em uma única função, para que fique claro como todo o cálculo ocorre especificamente para bitcoin e foi o que aconteceu:
Eu implementei essa função como um modelo c ++, ele pode operar não apenas com palavras de 32 bits, como uint32_t, mas também com palavras de um tipo diferente "T" da mesma maneira. Eu tenho aqui e o estado sha256 é armazenado como uma matriz do tipo "T" e sha256_transform () é chamado com um ponteiro de parâmetro para uma matriz do tipo "T" e o resultado é retornado da mesma forma. A função de transformação agora também está na forma de um modelo c ++:
template <typename T> T ror32(T word, unsigned int shift) { return (word >> shift) | (word << (32 - shift)); } template <typename T> T Ch(T x, T y, T z) { return z ^ (x & (y ^ z)); } template<typename T> T Maj(T x, T y, T z) { return (x & y) | (z & (x | y)); } #define e0(x) (ror32(x, 2) ^ ror32(x,13) ^ ror32(x,22)) #define e1(x) (ror32(x, 6) ^ ror32(x,11) ^ ror32(x,25)) #define s0(x) (ror32(x, 7) ^ ror32(x,18) ^ (x >> 3)) #define s1(x) (ror32(x,17) ^ ror32(x,19) ^ (x >> 10)) unsigned int ntohl(unsigned int in) { return ((in & 0xff) << 24) | ((in & 0xff00) << 8) | ((in & 0xff0000) >> 8) | ((in & 0xff000000) >> 24); } template <typename T> void LOAD_OP(int I, T *W, const u8 *input) { //W[I] = /*ntohl*/ (((u32*)(input))[I]); W[I] = ntohl(((u32*)(input))[I]); //W[I] = (input[3] << 24) | (input[2] << 16) | (input[1] << 8) | (input[0]); } template <typename T> void BLEND_OP(int I, T *W) { W[I] = s1(W[I - 2]) + W[I - 7] + s0(W[I - 15]) + W[I - 16]; } template <typename T> void sha256_transform(T *state, const T *input) { T a, b, c, d, e, f, g, h, t1, t2; TW[64]; int i; /* load the input */ for (i = 0; i < 16; i++) // MJ input is cast to u32* so this processes 16 DWORDS = 64 bytes W[i] = input[i]; /* now blend */ for (i = 16; i < 64; i++) BLEND_OP(i, W); /* load the state into our registers */ a = state[0]; b = state[1]; c = state[2]; d = state[3]; e = state[4]; f = state[5]; g = state[6]; h = state[7]; // t1 = h + e1(e) + Ch(e, f, g) + 0x428a2f98 + W[0]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x71374491 + W[1]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xb5c0fbcf + W[2]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xe9b5dba5 + W[3]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x3956c25b + W[4]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x59f111f1 + W[5]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x923f82a4 + W[6]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xab1c5ed5 + W[7]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xd807aa98 + W[8]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x12835b01 + W[9]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x243185be + W[10]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x550c7dc3 + W[11]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x72be5d74 + W[12]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x80deb1fe + W[13]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x9bdc06a7 + W[14]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xc19bf174 + W[15]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xe49b69c1 + W[16]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xefbe4786 + W[17]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x0fc19dc6 + W[18]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x240ca1cc + W[19]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x2de92c6f + W[20]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x4a7484aa + W[21]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x5cb0a9dc + W[22]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x76f988da + W[23]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x983e5152 + W[24]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xa831c66d + W[25]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xb00327c8 + W[26]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xbf597fc7 + W[27]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0xc6e00bf3 + W[28]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xd5a79147 + W[29]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x06ca6351 + W[30]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x14292967 + W[31]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x27b70a85 + W[32]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x2e1b2138 + W[33]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x4d2c6dfc + W[34]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x53380d13 + W[35]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x650a7354 + W[36]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x766a0abb + W[37]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x81c2c92e + W[38]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x92722c85 + W[39]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0xa2bfe8a1 + W[40]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0xa81a664b + W[41]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0xc24b8b70 + W[42]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0xc76c51a3 + W[43]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0xd192e819 + W[44]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xd6990624 + W[45]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0xf40e3585 + W[46]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x106aa070 + W[47]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x19a4c116 + W[48]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x1e376c08 + W[49]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x2748774c + W[50]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x34b0bcb5 + W[51]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x391c0cb3 + W[52]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0x4ed8aa4a + W[53]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0x5b9cca4f + W[54]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0x682e6ff3 + W[55]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; t1 = h + e1(e) + Ch(e, f, g) + 0x748f82ee + W[56]; t2 = e0(a) + Maj(a, b, c); d += t1; h = t1 + t2; t1 = g + e1(d) + Ch(d, e, f) + 0x78a5636f + W[57]; t2 = e0(h) + Maj(h, a, b); c += t1; g = t1 + t2; t1 = f + e1(c) + Ch(c, d, e) + 0x84c87814 + W[58]; t2 = e0(g) + Maj(g, h, a); b += t1; f = t1 + t2; t1 = e + e1(b) + Ch(b, c, d) + 0x8cc70208 + W[59]; t2 = e0(f) + Maj(f, g, h); a += t1; e = t1 + t2; t1 = d + e1(a) + Ch(a, b, c) + 0x90befffa + W[60]; t2 = e0(e) + Maj(e, f, g); h += t1; d = t1 + t2; t1 = c + e1(h) + Ch(h, a, b) + 0xa4506ceb + W[61]; t2 = e0(d) + Maj(d, e, f); g += t1; c = t1 + t2; t1 = b + e1(g) + Ch(g, h, a) + 0xbef9a3f7 + W[62]; t2 = e0(c) + Maj(c, d, e); f += t1; b = t1 + t2; t1 = a + e1(f) + Ch(f, g, h) + 0xc67178f2 + W[63]; t2 = e0(b) + Maj(b, c, d); e += t1; a = t1 + t2; state[0] += a; state[1] += b; state[2] += c; state[3] += d; state[4] += e; state[5] += f; state[6] += g; state[7] += h; }
O uso de funções de modelo C ++ é conveniente, pois eu posso calcular o hash necessário a partir de dados regulares e obter o resultado usual:
const uint8_t header[] = { 0x02,0x00,0x00,0x00, 0x17,0x97,0x5b,0x97,0xc1,0x8e,0xd1,0xf7, 0xe2,0x55,0xad,0xf2,0x97,0x59,0x9b,0x55, 0x33,0x0e,0xda,0xb8,0x78,0x03,0xc8,0x17, 0x01,0x00,0x00,0x00,0x00,0x00,0x00,0x00, 0x8a,0x97,0x29,0x5a,0x27,0x47,0xb4,0xf1, 0xa0,0xb3,0x94,0x8d,0xf3,0x99,0x03,0x44, 0xc0,0xe1,0x9f,0xa6,0xb2,0xb9,0x2b,0x3a, 0x19,0xc8,0xe6,0xba, 0xdc,0x14,0x17,0x87, 0x35,0x8b,0x05,0x53, 0x53,0x5f,0x01,0x19, 0x48,0x75,0x08,0x33 }; uint32_t test_nonce = 0x48750833; uint32_t result[8]; full_btc_hash(header, test_nonce, result); uint8_t* presult = (uint8_t * )result; for (int i = 0; i < 32; i++) printf("%02X ", presult[i]);
Acontece:
92 98 2A 50 91 FA BD 42 97 8A A5 CD 2D C9 36 28 02 4A DD FE E0 67 A4 78 00 00 00 00 00 00 00 00 00
No final do hash, existem muitos zeros, um belo hash, bingo, etc.
E agora, além disso, não posso passar dados uint32_t comuns para essa função de hash, mas minha classe C ++ especial, que redefinirá toda a aritmética.
Sim sim Vou aplicar a matemática probabilística "alternativa".
Eu mesmo inventei, percebi, experimentei. Parece não funcionar muito bem. Uma piada. Deveria funcionar. Talvez eu não seja o primeiro que estou tentando pôr em marcha.
Agora passamos ao mais interessante.
Toda aritmética na eletrônica digital é executada como operações em bits e é estritamente definida pelas operações AND, OR, NOT, EXCLUSIVE OR. Bem, todos sabemos o que são tabelas de verdade na álgebra booleana.
Sugiro acrescentar um pouco de incerteza aos cálculos, tornando-os probabilísticos.
Deixe que cada bit da palavra tenha não apenas os valores ZERO e UM possíveis, mas também todos os valores intermediários! Proponho considerar o valor de um bit como a probabilidade de um evento que pode ou não ocorrer. Se todos os dados iniciais forem conhecidos com segurança, o resultado será confiável. E se alguns dados estiverem faltando, o resultado será bastante provável.
De fato, suponha que haja dois eventos independentes “a” e “b”, cuja probabilidade de ocorrência é naturalmente de zero a um, respectivamente, Pa e Pb. Qual é a probabilidade de eventos acontecerem simultaneamente? Estou certo de que cada um de nós não hesitará em responder P = Pa * Pb e esta é a resposta correta!
O gráfico 3D dessa função terá a seguinte aparência (de dois pontos de vista diferentes):
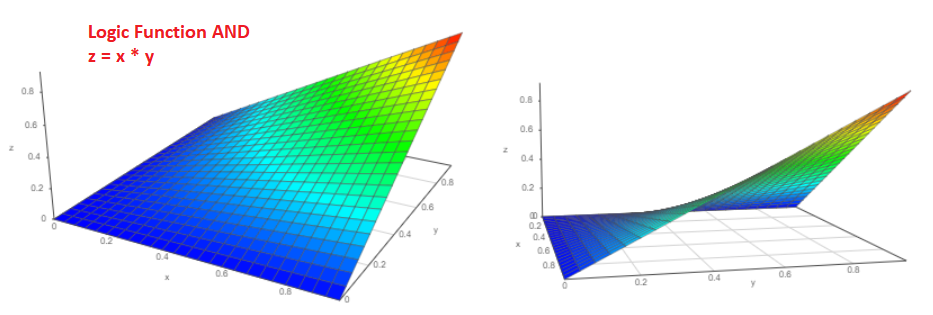
E qual é a probabilidade de que o evento Pa ou o evento Pb ocorra?
Probabilidade P = Pa + Pb-Pa * Pb. O gráfico da função é assim:
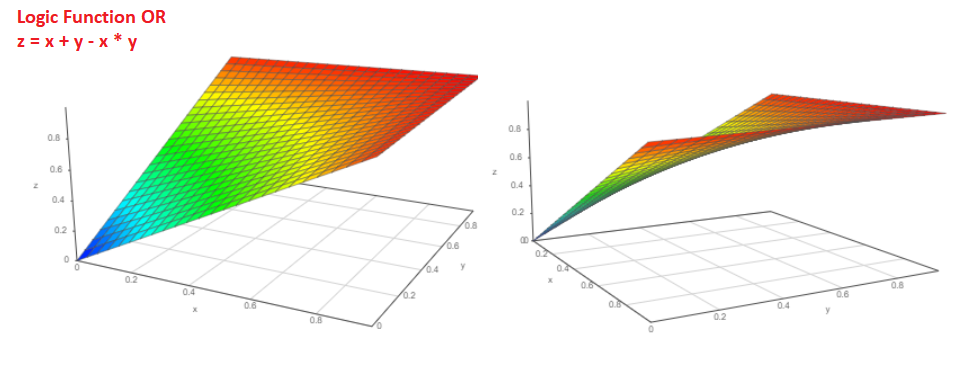
E se sabemos a probabilidade do evento Pa ocorrer, qual é a probabilidade de o evento não acontecer?
P = 1 - Pa.
Agora vamos fazer uma suposição. Imagine que temos elementos lógicos que calculam a probabilidade de um evento de saída, sabendo a probabilidade de eventos de entrada:
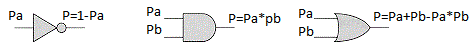
Ter esses elementos lógicos pode facilmente torná-los mais complexos, por exemplo, exclusivos ou XOR:
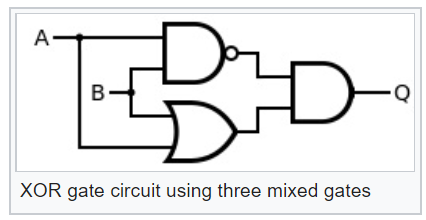
Agora, olhando o diagrama desse elemento lógico XOR, podemos entender qual será a probabilidade do evento na saída do XOR probabilístico:
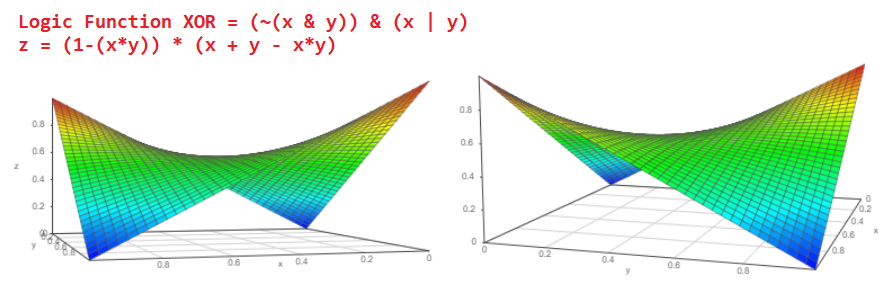
Mas isso não é tudo. Conhecemos a lógica típica de um somador completo e descobrimos como um somador de vários bits é feito a partir de um somador completo:
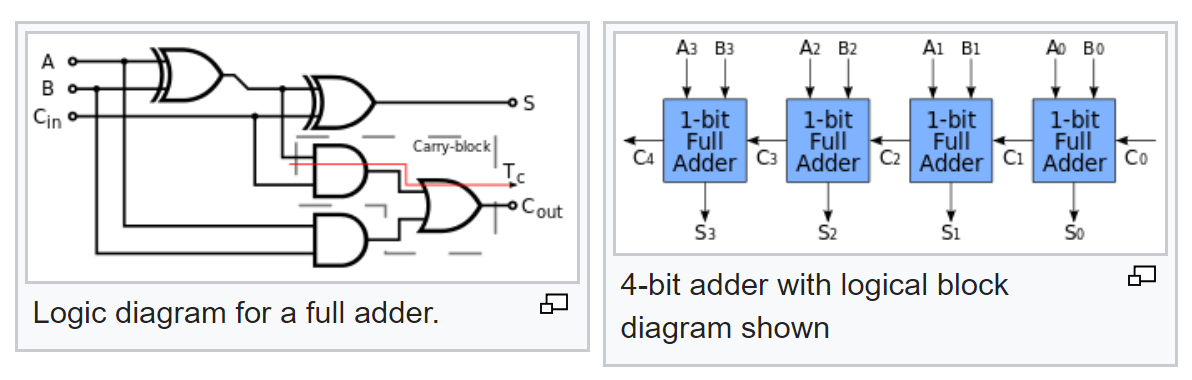
Então agora, de acordo com seu esquema, agora podemos calcular as probabilidades de sinais em sua saída, com probabilidades conhecidas de sinais na entrada.
Assim, eu posso implementar em c ++ minha própria classe de “32 bits” (chamarei de x32) com aritmética probabilística, redefinir todas as operações necessárias para sha256 como AND, OR, XOR, ADD e turnos nessa classe. A classe armazenará 32 bits dentro, mas cada bit é um número de ponto flutuante. Cada operação lógica ou aritmética em um número de 32 bits calculará a probabilidade do valor de cada bit com parâmetros de entrada conhecidos ou pouco conhecidos de uma operação lógica ou aritmética.
Considere um exemplo muito simples que usa minha matemática probabilística:
typedef std::numeric_limits< double > dbl; int main(int argc, char *argv[]) { cout.precision(dbl::max_digits10); x32 a = 0xaabbccdd; x32 b = 0x12345678; <b>
Neste exemplo, dois números de 32 bits são adicionados.
Enquanto a string é b.setBit (4, 0,75); O resultado da adição é comentado exatamente previsível e predeterminado, porque todos os dados de entrada para adição são conhecidos. O programa imprime isso no console:
result = 0xbcf02355 bit0 = 1 bit1 = 0 bit2 = 1 bit3 = 0 bit4 = 1 bit5 = 0 bit6 = 1 bit7 = 0 bit8 = 1 bit9 = 1 bit10 = 0 bit11 = 0 bit12 = 0 bit13 = 1 bit14 = 0 bit15 = 0 bit16 = 0 bit17 = 0 bit18 = 0 bit19 = 0 bit20 = 1 bit21 = 1 bit22 = 1 bit23 = 1 bit24 = 0 bit25 = 0 bit26 = 1 bit27 = 1 bit28 = 1 bit29 = 1 bit30 = 0 bit31 = 1
Se eu descomentar a linha b.setBit (4, 0,75); então, fazendo isso, diria ao programa: "adicione esses dois números para mim, mas eu realmente não sei o valor do bit 4 do segundo argumento, acho que é um com probabilidade de 0,75".
Então a adição ocorre, como deveria ser, com um cálculo completo das probabilidades dos sinais de saída, ou seja, bits:
bit not stable bit not stable bit not stable result = 0xbcf02305 bit0 = 1 bit1 = 0 bit2 = 1 bit3 = 0 bit4 = 0.75 bit5 = 0.1875 bit6 = 0.8125 bit7 = 0 bit8 = 1 bit9 = 1 bit10 = 0 bit11 = 0 bit12 = 0 bit13 = 1 bit14 = 0 bit15 = 0 bit16 = 0 bit17 = 0 bit18 = 0 bit19 = 0 bit20 = 1 bit21 = 1 bit22 = 1 bit23 = 1 bit24 = 0 bit25 = 0 bit26 = 1 bit27 = 1 bit28 = 1 bit29 = 1 bit30 = 0 bit31 = 1
Devido ao fato de os dados de entrada não serem muito conhecidos, o resultado não é muito conhecido. Além disso, o que pode ser calculado com segurança é considerado confiável. O que não pode ser contado é considerado com probabilidade.
Agora que tenho uma classe c ++ maravilhosa de 32 bits para aritmética difusa, posso passar matrizes de variáveis do tipo x32 para a função full_btc_hash () no modelo e obter um provável resultado estimado de hash.
Algumas das implementações da classe x32 são: #pragma once #include <string> #include <list> #include <iostream> #include <utility> #include <stdint.h> #include <vector> #include <limits> using namespace std; #include <boost/math/constants/constants.hpp> #include <boost/multiprecision/cpp_dec_float.hpp> using boost::multiprecision::cpp_dec_float_50; //typedef double MY_FP; typedef cpp_dec_float_50 MY_FP; class x32 { public: x32(); x32(uint32_t n); void init(MY_FP val); void init(double* pval); void setBit(int i, MY_FP val) { bvi[i] = val; }; ~x32() {}; x32 operator|(const x32& right); x32 operator&(const x32& right); x32 operator^(const x32& right); x32 operator+(const x32& right); x32& x32::operator+=(const x32& right); x32 operator~(); x32 operator<<(const unsigned int& right); x32 operator>>(const unsigned int& right); void print(); uint32_t get32(); MY_FP get_bvi(uint32_t idx) { return bvi[idx]; }; private: MY_FP not(MY_FP a); MY_FP and(MY_FP a, MY_FP b); MY_FP or (MY_FP a, MY_FP b); MY_FP xor(MY_FP a, MY_FP b); MY_FP bvi[32]; //bit values }; #include "stdafx.h" #include "x32.h" x32::x32() { for (int i = 0; i < 32; i++) { bvi[i] = 0.0; } } x32::x32(uint32_t n) { for (int i = 0; i < 32; i++) { bvi[i] = (n&(1 << i)) ? 1.0 : 0.0; } } void x32::init(MY_FP val) { for (int i = 0; i < 32; i++) { bvi[i] = val; } } void x32::init(double* pval) { for (int i = 0; i < 32; i++) { bvi[i] = pval[i]; } } x32 x32::operator<<(const unsigned int& right) { x32 t; for (int i = 31; i >= 0; i--) { if (i < right) { t.bvi[i] = 0.0; } else { t.bvi[i] = bvi[i - right]; } } return t; } x32 x32::operator>>(const unsigned int& right) { x32 t; for (unsigned int i = 0; i < 32; i++) { if (i >= (32 - right)) { t.bvi[i] = 0; } else { t.bvi[i] = bvi[i + right]; } } return t; } MY_FP x32::not(MY_FP a) { return 1.0 - a; } MY_FP x32::and(MY_FP a, MY_FP b) { return a * b; } MY_FP x32::or(MY_FP a, MY_FP b) { return a + b - a * b; } MY_FP x32::xor (MY_FP a, MY_FP b) { //(~(A & B)) & (A | B) return and( not( and(a,b) ) , or(a,b) ); } x32 x32::operator|(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = or ( bvi[i], right.bvi[i] ); } return t; } x32 x32::operator&(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = and (bvi[i], right.bvi[i]); } return t; } x32 x32::operator~() { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = not(bvi[i]); } return t; } x32 x32::operator^(const x32& right) { x32 t; for (int i = 0; i < 32; i++) { t.bvi[i] = xor (bvi[i], right.bvi[i]); } return t; } x32 x32::operator+(const x32& right) { x32 r; r.bvi[0] = xor (bvi[0], right.bvi[0]); MY_FP cout = and (bvi[0], right.bvi[0]); for (unsigned int i = 1; i < 32; i++) { MY_FP xor_a_b = xor (bvi[i], right.bvi[i]); r.bvi[i] = xor( xor_a_b, cout ); MY_FP and1 = and (bvi[i], right.bvi[i]); MY_FP and2 = and (xor_a_b, cout); cout = or (and1,and2); } return r; } x32& x32::operator+=(const x32& right) { MY_FP cout = and (bvi[0], right.bvi[0]); bvi[0] = xor (bvi[0], right.bvi[0]); for (unsigned int i = 1; i < 32; i++) { MY_FP xor_a_b = xor (bvi[i], right.bvi[i]); MY_FP and1 = and (bvi[i], right.bvi[i]); MY_FP and2 = and (xor_a_b, cout); bvi[i] = xor (xor_a_b, cout); cout = or (and1, and2); } return *this; } void x32::print() { for (int i = 0; i < 32; i++) { cout << bvi[i] << "\n"; } } uint32_t x32::get32() { uint32_t r = 0; for (int i = 0; i < 32; i++) { if (bvi[i] == 1.0) r = r | (1 << i); else if (bvi[i] == 0.0) { //ok } else { //oops.. cout << "bit not stable\n"; } } return r; }
Para que serve tudo isso?
O minerador de Bitcoin não sabe de antemão qual valor selecionar 32x nonce. O mineiro é forçado a repetir todos os 4 bilhões deles, a fim de contar o hash até que fique "bonito", até que o valor do hash se torne menor que o alvo.
A aritmética probabilística confusa teoricamente permite que você se livre de pesquisas exaustivas.
Sim, inicialmente eu não sei o significado de todos os bits não-necessários necessários. Se eu não os conheço, não deixe nada - a probabilidade inicial de não bits é de 0,5. Mesmo nesse cenário, posso calcular a probabilidade de bits de hash de saída. Em algum lugar, eles resultam em cerca de 0,5 mais ou menos meio centavo.
No entanto, agora eu posso alterar apenas um bit não-nulo de 0,5 para 0,9 ou 0,1 ou 1,0 e ver como o valor de probabilidade do valor do sinal de cada bit da função hash na saída é alterado. Agora eu tenho muito mais informações de avaliação. Agora posso sentir cada bit não-entrada individualmente e ver onde a probabilidade do sinal muda em cada um dos bits de saída da função hash.Por exemplo, aqui está um fragmento que considera uma função hash com bits nonse completamente desconhecidos, quando a probabilidade de seu valor de bit é 0,5 e o segundo cálculo, quando assumimos que o valor do bit nonce [0] = 0,9: typedef std::numeric_limits< double > dbl; int main(int argc, char *argv[]) { cout.precision(dbl::max_digits10);
A função de classe x32 :: get_bvi () retorna a probabilidade do valor de bit desse número.Calculamos e observamos que, se você alterar o valor do bit nonce [0] de 0,5 para 0,9, alguns bits da saída quase não aumentam e outros diminuem: 0.44525679540883948 0.44525679540840074 0.55268174813167364 0.5526817481315932 0.57758654725359399 0.57758654725360606 0.49595026978928474 0.49595026978930477 0.57118578561406703 0.57118578561407746 0.53237003739057907 0.5323700373905661 0.57269859374138096 0.57269859374138162 0.57631236396381141 0.5763123639638157 0.47943176373960149 0.47943176373960219 0.54955992675177704 0.5495599267517755 0.53321116270879686 0.53321116270879733 0.57294025883744952 0.57294025883744984 0.53131857821387693 0.53131857821387655 0.57253530821899101 0.57253530821899102 0.50661432403287194 0.50661432403287198 0.57149419848354913 0.57149419848354916 0.53220327148366491 0.53220327148366487 0.57268927270412251 0.57268927270412251 0.57632130426913003 0.57632130426913005 0.57233970084776142 0.57233970084776143 0.56824728628552812 0.56824728628552813 0.45247155441889921 0.45247155441889922 0.56875940568326509 0.56875940568326509 0.57524323439326321 0.57524323439326321 0.57587726902392535 0.57587726902392535 0.57597043124557292 0.57597043124557292 0.52847748894672118 0.52847748894672118 0.54512141953055808 0.54512141953055808 0.57362254577539695 0.57362254577539695 0.53082194129771177 0.53082194129771177 0.54404489702929382 0.54404489702929382 0.54065386336136847 0.54065386336136847
Uma espécie de sopro da brisa, uma mudança quase imperceptível na probabilidade de uma saída a 10m após o ponto decimal. Bem, no entanto ... você pode tentar criar algumas suposições sobre isso. Acontece lindamente, certo?A propósito, se os bits de entrada do nonse de entrada são inicializados com os valores de probabilidade corretos e necessários, como este: double nonce_bits[32]; for (int i = 0; i < 32; i++) nonce_bits[i] = (real_nonce32&(1 << i)) ? 1.0 : 0.0; x32 nonce_x32; nonce_x32.init(nonce_bits); full_btc_hash(strxx, nonce_x32, result_x32);
calculando o hash probabilístico, obtemos o resultado lógico correto - um hash “bonito” na saída, o bingo.Então, com a matemática, está tudo aqui.Resta aprender a analisar a respiração da brisa ... e o hash está quebrado.Parece bobagem, mas isso é bobagem - e eu avisei no começo.Outros materiais úteis:- Bitcoin mínimo com papel e caneta.
- É possível calcular bitcoins mais rápido, mais fácil ou mais fácil?
- Como eu fiz o blakecoin miner
- Mineiro FPGA Bitcoin no Mars rover board 3
- Mineiro de FPGA com algoritmo de Blake