Implementação de FPFT inteiro FFT

Olá pessoal!

Uma vez, os clientes me perguntaram se eu tinha FFT inteiro em meus projetos, ao qual eu sempre respondia que isso já havia sido feito por outras pessoas na forma de núcleos IP prontos, embora curvos, mas gratuitos (Altera / Xilinx) - pegue-o e use-o. No entanto, esses núcleos não são ótimos , possuem um conjunto de "recursos" e requerem refinamentos adicionais. Nesse contexto, tendo saído para outras férias planejadas, que eu não queria gastar medíocre, comecei a implementar o kernel configurável da FFT inteira.


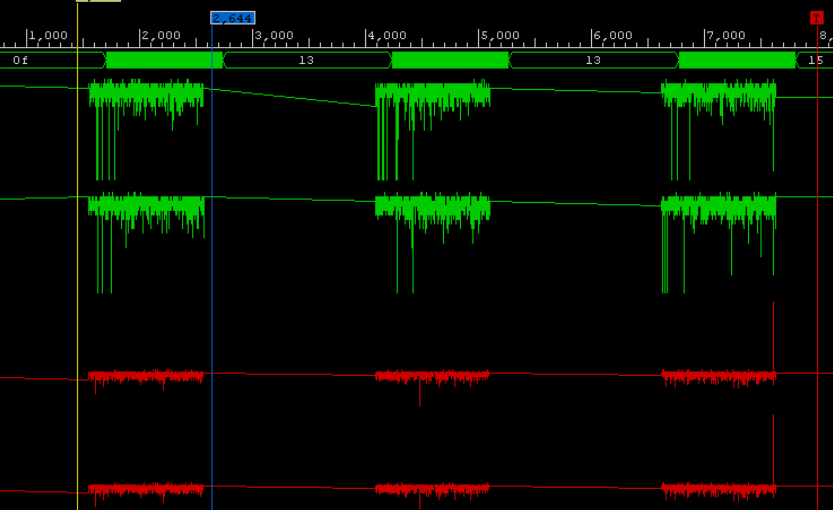_{KDPV (processo de depuração de erros de estouro de dados)}

No artigo, quero dizer a você por quais métodos e meios as operações matemáticas são realizadas ao calcular a transformada rápida de Fourier em um formato inteiro nos cristais modernos de FPGA. A base de qualquer FFT é um nó chamado "borboleta". A borboleta implementa operações matemáticas - adição, multiplicação e subtração. É sobre a implementação da "borboleta" e seus nós acabados que a história irá primeiro. Com base nas modernas famílias Xilinx FPGA - são as séries Ultrascale e Ultrascale +, assim como as séries mais antigas 6- (Virtex) e 7- (Artix, Kintex, Virtex) são afetadas. As séries mais antigas em projetos modernos não são de interesse em 2018. O objetivo do artigo é revelar os recursos da implementação de kernels personalizados do processamento de sinal digital usando o exemplo de uma FFT.

1. Introdução

Não é segredo para ninguém que os algoritmos para a tomada de FFT estão firmemente enraizados na vida dos engenheiros de processamento de sinais digitais e, portanto, essa ferramenta é constantemente necessária. Os principais fabricantes de FPGA, como o Altera / Xilinx, já possuem núcleos FFT / IFFT configuráveis ​​flexíveis, mas eles têm várias limitações e recursos e, portanto, tive que usar minha própria experiência mais de uma vez. Dessa vez, tive que implementar uma FFT em um formato inteiro, de acordo com o esquema Radix-2 no FPGA. No meu último artigo, eu já fiz FFT no formato de ponto flutuante e, a partir daí, você sabe que o algoritmo com duplo paralelismo é usado para implementar a FFT, ou seja, o núcleo pode processar duas amostras complexas na mesma frequência . Esse é um recurso essencial da FFT que não está disponível nos kernels prontos para Xilinx FFT.

Exemplo: é necessário desenvolver um nó FFT executando operação contínua do fluxo de entrada de números complexos a uma frequência de 800 MHz. O núcleo do Xilinx não fará isso (as freqüências de clock de processamento alcançáveis ​​nos modernos FPGAs são da ordem de 300-400 MHz) ou exigirá dizimar o fluxo de entrada de alguma forma. O núcleo personalizado permite registrar duas amostras de entrada a uma frequência de 400 MHz sem intervenção prévia, em vez de uma única amostra a 800 MHz. Outro ponto negativo do núcleo da Xilinx FFT é a incapacidade de aceitar o fluxo de entrada na ordem de reversão de bits . Nesse contexto, um grande recurso de memória de chips FPGA é gasto para reorganizar os dados em uma ordem normal. Para tarefas de rápida convolução de sinais, quando dois nós FFT ficam atrás um do outro, isso pode se tornar um momento crítico, ou seja, a tarefa simplesmente não estará no chip FPGA selecionado. O núcleo da FFT personalizado permite receber dados na ordem normal na entrada e enviá-los no modo de reversão de bits, enquanto o núcleo da FFT inversa - pelo contrário, recebe dados na ordem de reversão de bits e os envia no modo normal. Dois buffers para permutação de dados são salvos de uma vez !!!

Como a maior parte do material deste artigo pode se sobrepor ao anterior , decidi me concentrar no tópico de operações matemáticas em formato inteiro no FPGA para a implementação da FFT.

Parâmetros do kernel da FFT

• NFFT - número de borboletas (comprimento FFT),
• DATA_WIDTH - profundidade de bits dos dados de entrada (4-32),
• TWDL_WIDTH - profundidade de bit dos fatores de torneamento (8-27).
• SÉRIE - define a família FPGA na qual a FFT é implementada ("NEW" - Ultrascale, "OLD" - 6/7 da série Xilinx FPGA).

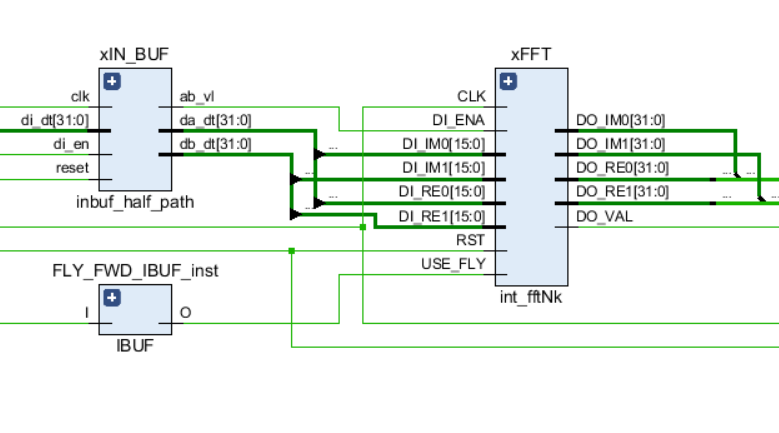
Como qualquer outro link no circuito, o FFT possui portas de controle de entrada - um sinal de relógio e um reset, além de portas de dados de entrada e saída. Além disso, o sinal USE_FLY é usado no kernel, o que permite desativar dinamicamente as borboletas FFT para processos de depuração ou para ver o fluxo de entrada original.

A tabela abaixo mostra a quantidade de recursos FPGA utilizados, dependendo do comprimento da NFFT FFT para DATA_WIDTH = 16 e dois bits TWDL_WIDTH = 16 e 24 bits.



O núcleo em NFFT = 64K é estável na frequência de processamento FREQ = 375 MHz em um cristal Kintex-7 (410T).

Estrutura do projeto

O gráfico esquemático do nó FFT é mostrado na figura a seguir:


Para facilitar a compreensão dos recursos de determinados componentes, darei uma lista dos arquivos do projeto e sua breve descrição em uma ordem hierárquica:

• Núcleos FFT:
  
  • int_fftNk - nó FFT, circuito Radix-2, dizimação de frequência (DIF), fluxo de entrada normal, fluxo de saída inverso de bits.
  • int_ifftNk - nó OBPF , circuito Radix-2, dizimação de tempo (DIT), fluxo de entrada com inversão de bits, fluxo de saída normal.
• Borboletas:
  
  
  • int_dif2_fly - borboleta Radix-2, dizimação em frequência,
  • int_dit2_fly - borboleta Radix-2, dizimação no tempo,
• Multiplicadores complexos:
  
  
  • int_cmult_dsp48 - multiplicador configurável geral, inclui:
  • int_cmult18x25_dsp48 - multiplicador para pequenas profundidades de bits dos dados e fatores de rotação,
  • int_cmult_dbl18_dsp48 - multiplicador dobrado, largura de bit dos fatores de torneamento de até 18 bits,
  • int_cmult_dbl35_dsp48 - multiplicador dobrado, largura dos bits dos fatores de rotação de até 25 * bits,
  • int_cmult_trpl18_dsp48 - multiplicador triplo, a capacidade dos fatores de torneamento de até 18 bits,
  • int_cmult_trpl52_dsp48 - multiplicador triplo, a capacidade dos fatores de rotação de até 25 * bits,
• Multiplicadores:
  
  
  • mlt42x18_dsp48e1 - um multiplicador com bits de operandos de até 42 e 18 bits com base no DSP48E1,
  • mlt59x18_dsp48e1 - multiplicador com bits de operando de até 59 e 18 bits com base no DSP48E1,
  • mlt35x25_dsp48e1 - um multiplicador com bits de operandos de até 35 e 25 bits com base no DSP48E1,
  • mlt52x25_dsp48e1 - um multiplicador com bits de operandos de até 52 e 25 bits com base no DSP48E1,
  • mlt44x18_dsp48e2 - multiplicador com bits de operandos de até 44 e 18 bits com base no DSP48E2,
  • mlt61x18_dsp48e2 - multiplicador com bits de operando de até 61 e 18 bits com base no DSP48E2,
  • mlt35x27_dsp48e2 - multiplicador com bits de operando de até 35 e 27 bits com base no DSP48E2,
  • mlt52x27_dsp48e2 é um multiplicador com bits de operando de até 52 e 27 bits com base no DSP48E2.
• Totalizador:
  
  
  • int_addsub_dsp48 - somador universal, bits de operando de até 96 bits.
• Linhas de atraso:
  
  
  • int_delay_line - a linha de base do atraso, fornece uma permutação de dados entre borboletas,
  • int_align_fft - alinhamento dos dados de entrada e os fatores de viragem na entrada da borboleta FFT,
  • int_align_fft - alinhamento dos dados de entrada e os fatores de viragem na entrada da borboleta OBPF ,
• Fatores rotativos:
  
  
  • rom_twiddle_int - um gerador de fatores rotativos, de um certo comprimento a FFT considera coeficientes baseados em células DSP FPGA,
  • row_twiddle_tay - gerador de fatores rotativos usando uma série de Taylor (NFFT> 2K) **.
• Buffer de dados:
  
  
  • inbuf_half_path - buffer de entrada, recebe o fluxo no modo normal e produz duas seqüências de amostras deslocadas pela metade do comprimento da FFT ***,
  • outbuf_half_path - o buffer de saída, coleta duas seqüências e produz uma contínua igual ao comprimento da FFT,
  • iobuf_flow_int2 - o buffer funciona em dois modos: recebe um fluxo no modo Interleave-2 e produz duas seqüências de FFT deslocadas pela metade do comprimento. Ou vice-versa, dependendo da opção BITREV.
  • int_bitrev_ord é um simples conversor de dados da ordem natural para a reversão de bits.

* - para DSP48E1: 25 bits, para DSP48E2 - 27 bits.
** - a partir de um certo estágio da FFT, uma quantidade fixa de memória de bloco pode ser usada para armazenar coeficientes de rotação e coeficientes intermediários podem ser calculados usando nós DSP48, usando a fórmula de Taylor para a primeira derivada. Devido ao fato de que o recurso de memória é mais importante para a FFT, você pode sacrificar com segurança as unidades de computação em prol da memória.
*** - buffer de entrada e linhas de atraso - contribuem significativamente para a quantidade de recursos de memória FPGA ocupados

Borboleta

Todo mundo que encontrou pelo menos uma vez o algoritmo de transformação rápida de Fourier sabe que esse algoritmo é baseado em uma operação elementar - uma "borboleta". Ele converte o fluxo de entrada multiplicando a entrada pelo fator twiddle. Existem dois esquemas de conversão clássicos para FFTs - dizimação em frequência (DIF, dizimação em frequência) e dizimação no tempo (DIT, dizimação em tempo). O algoritmo DIT é caracterizado pela divisão da sequência de entrada em duas sequências de meia duração, e o algoritmo DIF em duas sequências de amostras pares e ímpares de duração NFFT. Além disso, esses algoritmos diferem em operações matemáticas para a operação borboleta.



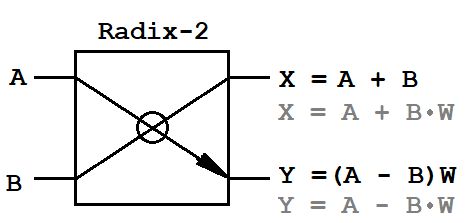A, B - pares de entrada de amostras complexas,
X, Y - pares de saída de amostras complexas,
W - fatores de torneamento complexos.

Como os dados de entrada são quantidades complexas, a borboleta requer um multiplicador complexo (4 operações de multiplicação e 2 operações de adição) e dois somadores complexos (4 operações de adição). Essa é toda a base matemática que deve ser implementada no FPGA.

Multiplicador

Deve-se notar que todas as operações matemáticas nos FPGAs são frequentemente executadas em código adicional (complemento 2). O multiplicador FPGA pode ser implementado de duas maneiras - na lógica, usando gatilhos e tabelas LUT, ou em unidades especiais de cálculo DSP48, que foram incluídas longa e firmemente em todos os FPGAs modernos. Em blocos lógicos, a multiplicação é implementada usando o algoritmo Booth ou suas modificações, consome uma quantidade decente de recursos lógicos e nem sempre satisfaz as restrições de tempo em altas frequências de processamento de dados. Nesse sentido, multiplicadores FPGA em projetos modernos quase sempre são projetados com base em nós DSP48 e apenas ocasionalmente na lógica. Um nó DSP48 é uma célula final complexa que implementa funções matemáticas e lógicas. Operações básicas: multiplicação, adição, subtração, acumulação, contador, operações lógicas (XOR, NAND, AND, OR, NOR), quadratura, comparação de números, turno, etc. A figura a seguir mostra a célula DSP48E2 da família Xilinx Ultrascale + FPGA.



Por meio de uma configuração simples das portas de entrada, operações de cálculo nos nós e atrasos de configuração dentro do nó, você pode fazer uma debulhadora de dados matemáticos de alta velocidade.
Observe que todos os principais fornecedores de FPGA no ambiente de desenvolvimento possuem núcleos de IP padrão e livres para calcular funções matemáticas com base no nó DSP48. Eles permitem calcular funções matemáticas primitivas e definir vários atrasos na entrada e saída do nó. Para o Xilinx, esse é o “multiplicador” do IP-Core (versão 12.0, 2018), que permite configurar o multiplicador para qualquer profundidade de dados de entrada de 2 a 64 bits. Além disso, você pode especificar como o multiplicador é implementado - em recursos lógicos ou em primitivas DSP48 integradas.

Estime quanta lógica o multiplicador “come” com a profundidade de bits dos dados de entrada nas portas A e B = 64 bits. Se você usar os nós DSP48, eles precisarão de apenas 16.



A principal limitação nas células DSP48 é a profundidade de bits dos dados de entrada. O nó DSP48E1, que é a célula base das séries FPGA Xilinx 6 e 7, a largura das portas de entrada para multiplicação: “A” - 25 bits, “B” - 18 bits. Portanto, o resultado da multiplicação é um número de 43 bits. Para a família Xilinx Ultrascale e Ultrascale + FPGA, o nó passou por várias alterações, em particular, a capacidade da primeira porta aumentada em dois bits: “A” - 27 bits, “B” - 18 - bits. Além disso, o próprio nó é chamado DSP48E2.

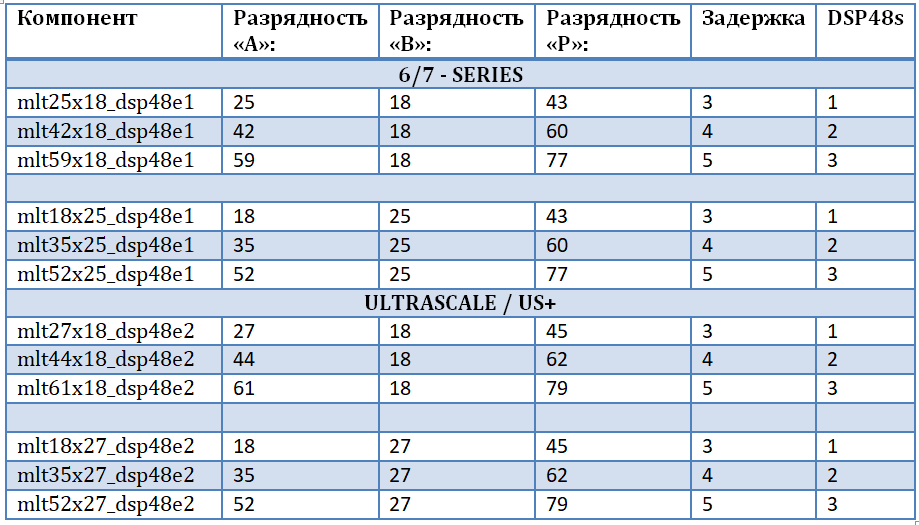
Para não ficar vinculado a uma família específica e ao chip FPGA, para garantir a "pureza do código fonte" e levar em consideração todas as profundidades de bits possíveis dos dados de entrada, foi decidido projetar nosso próprio conjunto de multiplicadores. Isso permitirá a implementação mais eficiente de multiplicadores complexos para borboletas FFT, ou seja, multiplicadores e um somador-subtrator baseado em blocos DSP48. A primeira entrada do multiplicador são os dados de entrada, a segunda entrada do multiplicador são os fatores rotativos (sinal harmônico da memória). Um conjunto de multiplicadores é implementado usando a biblioteca UNISIM integrada, a partir da qual é necessário conectar as primitivas DSP48E1 e DSP48E2 para uso posterior no projeto. Um conjunto de multiplicadores é apresentado na tabela. Note-se que:

• A operação de multiplicação de números leva a um aumento na capacidade do produto como a soma da capacidade dos operandos.
• Cada um dos multiplicadores 25x18 e 27x18 é duplicado, de fato - este é um componente para famílias diferentes.
• Quanto maior o estágio de paralelismo da operação, maior o atraso na computação e maior a quantidade de recursos ocupados.
• Com menor profundidade de bit na entrada “B”, multiplicadores com maior profundidade de bit em outra entrada podem ser implementados.
• A principal limitação no aumento da profundidade de bits é introduzida pela porta “B” (a porta real da primitiva DSP48) e o registro de deslocamento interno em 17 bits.

Um aumento adicional na profundidade de bits não interessa na estrutura da tarefa pelos motivos descritos abaixo:

Profundidade de bit dos fatores de torneamento

Sabe-se que quanto maior a resolução do sinal harmônico, mais preciso o número aparece (mais sinais na parte fracionária). Mas o tamanho do bit da porta é B <25 bits devido ao fato de que, para os fatores rotacionais nos nós da FFT, essa profundidade de bits é suficiente para garantir uma multiplicação de alta qualidade do fluxo de entrada com elementos de sinal harmônico nas "borboletas" (para qualquer comprimento de FFT realístico possível nos FPGAs modernos). O valor típico da profundidade de bits dos coeficientes de torneamento nas tarefas que estou implementando é 16 bits, 24 - menos frequentemente, 32 - nunca.

Profundidade de bits das amostras de entrada

A capacidade desses nós de recepção e gravação típicos (ADCs, DACs) não é grande - de 8 a 16 bits e raramente - 24 ou 32 bits. Além disso, no último caso, é mais eficiente usar o formato de dados de ponto flutuante de acordo com o padrão IEEE-754. Por outro lado, cada estágio da “borboleta” na FFT adiciona um bit de dados às amostras de saída devido a operações matemáticas. Por exemplo, para um comprimento de NFFT = 1024, log2 (NFFT) = 10 borboletas é usado.

Portanto, a profundidade do bit de saída será dez bits maior que a entrada, WOUT = WIN + 10. Em geral, a fórmula fica assim:

WOUT = WIN + log2 (NFFT);

Um exemplo:

Profundidade de bits do fluxo de entrada WIN = 32 bits,
Profundidade de bit dos fatores de torneamento TWD = 27,
A capacidade da porta "A" da lista de multiplicadores implementados neste artigo não excede 52 bits. Isso significa que o número máximo de borboletas é FFT = 52-32 = 20. Ou seja, é possível realizar a FFT com um comprimento de até 2 ^ 20 = 1M de amostras. (No entanto, na prática, isso não é possível por meios diretos devido aos recursos limitados, mesmo para os cristais FPGA mais poderosos, mas isso se relaciona a outro tópico e não será considerado no artigo).

Como você pode ver, essa é uma das principais razões pelas quais eu não implementei multiplicadores com maior profundidade de bits nas portas de entrada. Os multiplicadores usados ​​cobrem toda a gama de tamanhos de bits de entrada necessários e fatores de rotação para a tarefa de calcular a FFT inteira. Em todos os outros casos, você pode usar o cálculo da FFT no formato de ponto flutuante !

A implementação do multiplicador "amplo"

Com base em um exemplo simples de multiplicar dois números que não se encaixam na profundidade de bits de um nó DSP48 padrão, mostrarei como você pode implementar um amplo multiplicador de dados. A figura a seguir mostra seu diagrama de blocos. O multiplicador implementa a multiplicação de dois números assinados no código adicional, a largura do primeiro operando X é de 42 bits, o segundo Y é de 18 bits. Ele contém dois nós DSP48E2. Dois registros são usados ​​para equalizar atrasos no nó superior. Isso é feito porque no somador superior você precisa adicionar corretamente os números dos nós superiores e inferiores do DSP48. O somador de baixo não é realmente usado. Na saída do nó inferior, há um atraso adicional do produto para alinhar o número de saída com o tempo. O atraso total é de 4 ciclos.



O trabalho consiste em dois componentes:

• A parte mais jovem: P1 = '0' e X [16: 0] * Y [17: 0];
• A parte mais antiga: P2 = X [42:17] * Y [17: 0] + (P1 >> 17);

Totalizador

Como um multiplicador, um somador pode ser construído com recursos lógicos usando uma cadeia de transferência ou em blocos DSP48. Para alcançar o rendimento máximo, um segundo método é preferível. Uma primitiva DSP48 permite implementar a operação de adição de até 48 bits, dois nós de até 96 bits. Para a tarefa atual, essas profundidades de bits são suficientes. Além disso, a primitiva DSP48 possui um modo "SIMD MODE" especial, que paralela a ALU de 48 bits incorporada em várias operações com dados diferentes de pequena capacidade. Ou seja, no modo "UM", uma grade de bits completa de 48 bits e dois operandos são usados, e no modo "DOIS", a grade de bits é dividida em várias correntes paralelas de 24 bits cada (4 operandos). Esse modo, usando apenas um somador, ajuda a reduzir a quantidade de recursos de chips FPGA ocupados em pequenas profundidades de bits de amostras de entrada (nos primeiros estágios do cálculo).

Aumento da profundidade de bits

A operação de multiplicar dois números pelos bits N e M em um código adicional binário leva a um aumento na capacidade do bit de saída para P = N + M.

Exemplo: para multiplicar números de três bits N = M = 3, o número positivo máximo é +3 ​​= (011) ₂ e o número negativo máximo é 4 = (100) ₂ . O bit mais significativo é responsável pelo sinal do número. Portanto, o número máximo possível ao multiplicar é +16 = (010000) ₂ , que é formado como resultado da multiplicação de dois números negativos máximos -4. A profundidade de bits da saída é igual à soma dos bits de entrada P = N + M = 6 bits.

A operação de adição de dois números com os bits N e M no código adicional binário leva a um aumento no bit de saída em um bit.

Exemplo: adicione dois números positivos, N = M = 3, o número positivo máximo é 3 = (011) ₂ e o número negativo máximo é 4 = (100) ₂ . . , – 6 = (0110) ₂ , – -8 = (1000) ₂ . .

:
. . , 16- -32768 = 0x8000, -32767 = 0x8001. ~0.003% .

, . : – 4 = (100) ₂ , +3 = (011) ₂. Resultado da Multiplicação = -12 = (110100) ₂ . O quinto bit pode ser descartado porque ele duplica o vizinho, o quarto é um sinal.

Truncamento de bits abaixo:

, «» , , . M- , , . 0x8000 = -1, 0x7FFF = +1. , ( M ). , , 1 . , [N+M-1-1: M-1]. ( 1), – .

/ «» .

, FFT DIT FFT DIF W0 = {Re, Im} = {1, 0}. , – , . : «» . : W0 = {Re, Im} = {1, 0} W1 = {Re, Im} = {0, -1}. , . DSP48 .

– -, , .

- , . . — — .

INT_FFTK

• .
• NFFT = 8-512K .
• NFFT.
• , .
• , .
• .
• !
• .
• : – , -.
• : - , – .
• . Radix-2.
• NFFT *.
• .
• (Virtex-6, 7-Series, Ultrascale).
• ~375MHz Kintex-7
• – VHDL.
• bitreverse +.
• Open Source IP-Cores.

INTFFTK VHDL ( ) m- Matlab / Octave .

Conclusão

, . , . , IP-CORE Xilinx. .

: Radix-4, Radix-8, Ultra-Long FFT , FFT-FP32 ( IEEE-754). , , . FFT Radix-8, ( ).

dsmv2014 , . Obrigado pela atenção!

UPDATE 2018/08/22

SCALED FFT / IFFT . 1 (truncate LSB). = .

, , : . , - .

: — 6 . — 128 . NFFT = 1024 , DATA_WIDTH = 16, TWDL_WIDTH = 16.

, SCALED « » , UNSCALED .