Visão Geral do Algoritmo da Entrevista de Trabalho - Geração de Conjunto

Olá Habr!

Este post inicia a análise de tarefas nos algoritmos que grandes empresas de TI (Mail.Ru Group, Google etc.) adoram dar candidatos a entrevistas (se a entrevista com algoritmos não for boa, então as chances de conseguir um emprego em uma empresa de sonho, infelizmente tendem a zero). Antes de tudo, este post é útil para aqueles que não têm experiência em programação de olimpíadas ou cursos pesados ​​como ShAD ou LKS, nos quais os tópicos de algoritmos são levados a sério o suficiente, ou para quem deseja atualizar seus conhecimentos em um determinado campo.

Ao mesmo tempo, não se pode argumentar que todas as tarefas que serão tratadas aqui certamente serão cumpridas na entrevista; no entanto, as abordagens pelas quais essas tarefas são resolvidas são semelhantes na maioria dos casos.

A narração será dividida em diferentes tópicos, e começaremos gerando conjuntos com uma estrutura específica.

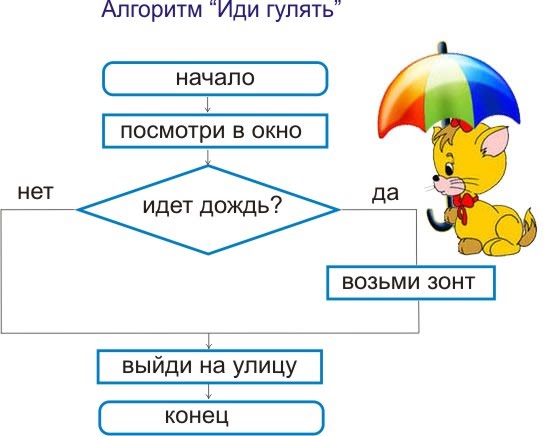
1. Vamos começar com o acordeão de botão: você precisa gerar todas as seqüências de colchetes corretas com colchetes do mesmo tipo ( qual é a sequência de colchetes correta ), onde o número de colchetes é k.

Este problema pode ser resolvido de várias maneiras. Vamos começar com recursiva .

Esse método pressupõe que estamos começando a iterar as seqüências de uma lista vazia. Depois que o colchete (abertura ou fechamento) é adicionado à lista, a chamada de recursão é novamente executada e as condições são verificadas. Quais são as condições? É necessário monitorar a diferença entre colchetes de abertura e fechamento (variável cnt ) - você não pode adicionar um colchete à lista se essa diferença não for positiva; caso contrário, a sequência de colchetes deixará de estar correta. Resta implementar isso cuidadosamente no código.

 k = 6 #   init = list(np.zeros(k)) #  ,    cnt = 0 #    ind = 0 # ,       def f(cnt, ind, k, init): #  . ,     if (cnt <= k-ind-2): init[ind] = '(' f(cnt+1, ind+1, k, init) # .    ,  cnt > 0 if cnt > 0: init[ind] = ')' f(cnt-1, ind+1, k, init) #      if ind == k: if cnt == 0: print (init) 

A complexidade desse algoritmo é $$$O ((C_k ^ {k / 2} - C_k ^ {k / 2 -1}) * k)$memória adicional necessária $$$O (k)$.

Com os parâmetros fornecidos, a chamada de função $$$f (cnt, ind, k, init)$produzirá o seguinte:

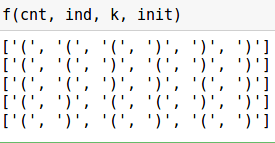
Uma maneira iterativa de resolver esse problema: nesse caso, a idéia será fundamentalmente diferente - você precisará introduzir o conceito de ordem lexicográfica para sequências de colchetes.

Todas as seqüências de parênteses corretas para um tipo de parêntese podem ser ordenadas, levando em consideração o fato de que $$$'(' <')'$. Por exemplo, para n = 6, a sequência mais lexicograficamente mais baixa é $$$((()))$e o mais velho - $$$() () ()$.

Para obter a próxima sequência lexicográfica, você precisa encontrar o colchete de abertura mais à direita, antes do qual haja um colchete de fechamento, para que, quando eles sejam trocados em alguns lugares, a sequência de colchetes permaneça correta. Nós os trocamos e tornamos o sufixo o menor mais lexicográfico - para isso, você precisa calcular a cada passo a diferença entre o número de colchetes.

Na minha opinião, essa abordagem é um pouco sombria do que recursiva, mas pode ser usada para resolver outros problemas de grupos geradores. Nós implementamos isso no código.

 #  ,    n = 6 arr = ['(' for _ in range(n//2)] + [')' for _ in range(n//2)] def f(n, arr): #    print (arr) while True: ind = n-1 cnt = 0 #  . ,    while ind>=0: if arr[ind] == ')': cnt -= 1 if arr[ind] == '(': cnt += 1 if cnt < 0 and arr[ind] =='(': break ind -= 1 #   ,     if ind < 0: break #   .  arr[ind] = ')' #      for i in range(ind+1,n): if i <= (n-ind+cnt)/2 +ind: arr[i] = '(' else: arr[i] = ')' print (arr) 

A complexidade desse algoritmo é a mesma do exemplo anterior.

A propósito, existe um método simples que demonstra que o número de seqüências de colchetes geradas para um dado n / 2 deve corresponder aos números catalães .

Isso funciona!

Ótimo, com os colchetes, por enquanto, vamos passar a gerar subconjuntos. Vamos começar com um quebra-cabeça simples.

2. Dada uma matriz de ordem crescente com números de $$$0$antes $$$n-1$, é necessário gerar todos os seus subconjuntos.

Observe que o número de subconjuntos desse conjunto é exatamente $$$2 ^ n$. Se cada subconjunto for representado como uma matriz de índices, em que $$$0$significa que o elemento não está incluído no conjunto, mas $$$1$- o que está incluído, a geração de todas essas matrizes será a geração de todos os subconjuntos.

Se considerarmos a representação bit a bit de números de 0 a $$$2 ^ n - 1$, eles especificarão os subconjuntos desejados. Ou seja, para resolver o problema, é necessário implementar a adição de unidade a um número binário. Começamos com todos os zeros e terminamos com uma matriz na qual há uma unidade.

 n = 3 B = np.zeros(n+1) #  B   1  (    ) a = np.array(list(range(n))) #   def f(B, n, a): #   while B[0] == 0: ind = n #     while B[ind] == 1: ind -= 1 #   1 B[ind] = 1 #      B[(ind+1):] = 0 print (a[B[1:].astype('bool')]) 

A complexidade desse algoritmo é $$$O (n * 2 ^ n)$, de memória - $$$O (n)$.

Agora vamos complicar um pouco a tarefa anterior.

3. Dada uma matriz ordenada em ordem crescente com números de $$$0$antes $$$n-1$, você precisa gerar tudo isso $$$k$subconjuntos de elementos (resolvidos iterativamente).

Observo que a formulação deste problema é semelhante à anterior e pode ser resolvida usando aproximadamente a mesma metodologia: pegue a matriz inicial com $$$k$unidades e $$$n-k$zeros e iteram em todas as variantes de tais seqüências de comprimento $$$n.$

No entanto, pequenas alterações são necessárias. Precisamos resolver tudo $$$k$conjuntos de números $$$0$antes $$$n-1$. Você precisa entender exatamente como precisa classificar os subconjuntos. Nesse caso, podemos introduzir o conceito de ordem lexicográfica para esses conjuntos.

Também organizamos a sequência por códigos de caracteres: $$$1 <0$(Isso, é claro, é estranho, mas é necessário, e agora vamos entender o porquê). Por exemplo, para $$$n = 4, k = 2$o mais novo e o mais velho será a sequência $$$[1,1,0,0]$e $$$[0,0,1,1]$.

Resta entender como descrever a transição de uma sequência para outra. Tudo é simples aqui: se mudarmos $$$1$em $$$0$, então, à esquerda, escrevemos o mínimo lexicograficamente, levando em consideração a preservação da condição em $$$k$. Código:

 n = 5 k = 3 a = np.array(list(range(n))) #    k -   init = [1 for _ in range(k)] + [0 for _ in range(nk)] def f(a, n, k, init): #   k-  print (a[a[init].astype('bool')]) while True: unit_cnt = 0 cur_ind = 0 #   ,     1 while (cur_ind < n) and (init[cur_ind]==1 or unit_cnt==0): if init[cur_ind] == 1: unit_cnt += 1 cur_ind += 1 #        -    if cur_ind == n: break #  init[cur_ind] = 1 #   . .  for i in range(cur_ind): if i < unit_cnt-1: init[i] = 1 else: init[i] = 0 print (a[a[init].astype('bool')]) 

Exemplo de trabalho:

A complexidade desse algoritmo é $$$O (C_n ^ k * n)$, de memória - $$$O (n)$.

4. Dada uma matriz de ordem crescente com números de $$$0$antes $$$n-1$, você precisa gerar tudo isso $$$k$subconjuntos de elementos (resolver recursivamente).

Agora vamos tentar a recursão. A ideia é simples: desta vez sem descrição, veja o código.

 n = 5 a = np.array(list(range(n))) ind = 0 # ,       num = 0 # ,       k = 3 sub = list(-np.ones(k)) #  def f(n, a, num, ind, k, sub): #   k  ,     if ind == k: print (sub) else: for i in range(n - num): #  ,      k  if (n - num - i >= k - ind): #      sub[ind] = a[num + i] #     f(n, a, num+1+i, ind+1, k, sub) 

Exemplo de trabalho:

A complexidade é a mesma do método anterior.

5. Dada uma matriz de ordem crescente com números de $$$0$antes $$$n-1$, é necessário gerar todas as suas permutações.

Vamos resolver usando recursão. A solução é semelhante à anterior, onde temos uma lista auxiliar. Inicialmente é zero se estiver $$$i$-ésimo lugar do elemento é uma unidade, então o elemento $$$i$já na permutação. Mal disse o que fez:

 a = np.array(range(3)) n = a.shape[0] ind_mark = np.zeros(n) #   perm = -np.ones(n) #     def f(ind_mark, perm, ind, n): if ind == n: print (perm) else: for i in range(n): if not ind_mark[i]: #     ind_mark[i] = 1 #   perm[ind] = i f(ind_mark, perm, ind+1, n) #   -    ind_mark[i] = 0 

Exemplo de trabalho:

A complexidade desse algoritmo é $$$O (n ^ 2 * n!)$, de memória - $$$O (n).$

Agora considere dois quebra-cabeças muito interessantes para os códigos Gray . Em poucas palavras, este é um conjunto de seqüências do mesmo comprimento, em que cada sequência difere dos vizinhos em uma categoria.

6. Gere todos os códigos bidimensionais de comprimento cinza n.

A idéia de resolver esse problema é legal, mas se você não conhece a solução, pode ser muito difícil pensar. Noto que o número de tais seqüências é $$$2 ^ n$.

Vamos resolver iterativamente. Suponha que tenhamos gerado parte de tais seqüências e elas estejam em alguma lista. Se duplicarmos uma lista e a escrevermos na ordem inversa, a última sequência na primeira lista coincidirá com a primeira na segunda lista, a penúltima coincidirá com a segunda, etc. Combine essas listas em uma.

O que precisa ser feito para que todas as seqüências na lista sejam diferentes na mesma categoria? Coloque uma unidade nos locais apropriados nos elementos da segunda lista para obter os códigos Gray.

É difícil perceber "de ouvido", descreveremos as iterações desse algoritmo.

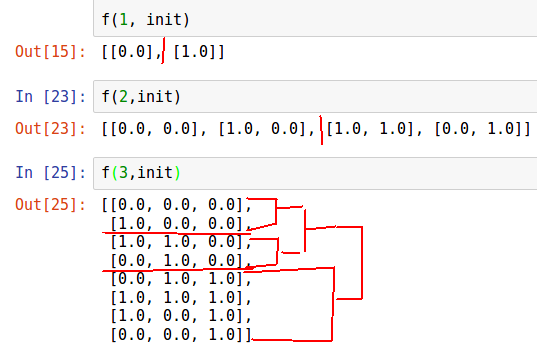
 n = 3 init = [list(np.zeros(n))] def f(n, init): for i in range(n): for j in range(2**i): init.append(list(init[2**i - j - 1])) init[-1][i] = 1.0 return init 

A complexidade desta tarefa é $$$O (n * 2 ^ n)$, de memória o mesmo.

Agora vamos complicar a tarefa.

7. Gere todos os códigos cinzentos k-dimensionais de comprimento n.

É claro que a tarefa passada é apenas um caso especial dessa tarefa. No entanto, dessa maneira bonita em que a tarefa passada foi resolvida, isso não pode ser resolvido; aqui é necessário classificar as seqüências na ordem correta. Vamos obter uma matriz bidimensional $$$k * n$. Inicialmente, a última linha possui unidades e o restante possui zeros. Além disso, na matriz, $$$-1$. Aqui $$$1$e $$$-1$diferem um do outro na direção: $$$1$aponta para cima $$$-1$aponta para baixo. Importante: em cada coluna, a qualquer momento, pode haver apenas um $$$1$ou $$$-1$, e os números restantes serão zeros.

Agora vamos entender como é possível classificar essas seqüências para obter os códigos Gray. Comece do final para mover o elemento para cima.

No próximo passo, atingimos o teto. Nós escrevemos a sequência resultante. Depois de atingir o limite, você precisa começar a trabalhar com a próxima coluna. Você precisa procurá-lo da direita para a esquerda e, se encontrarmos uma coluna que pode ser movida, para todas as colunas com as quais não conseguimos trabalhar, as setas mudarão na direção oposta para que possam ser movidas novamente.

Agora você pode mover a primeira coluna para baixo. Nós a movemos até atingir o chão. E assim por diante, até que todas as setas batam no chão ou no teto e não restem colunas que possam ser movidas.

No entanto, na estrutura de economia de memória, resolveremos esse problema usando duas matrizes unidimensionais de comprimento $$$n$: em uma matriz os próprios elementos da sequência estarão e na outra de sua direção (setas).

 n,k = 3,3 arr = np.zeros(n) direction = np.ones(n) #   ,    def k_dim_gray(n,k): #    print (arr) while True: ind = n-1 while ind >= 0: #    ,    if (arr[ind] == 0 and direction[ind] == 0) or (arr[ind] == k-1 and direction[ind] == 1): direction[ind] = (direction[ind]+1)%2 else: break ind -= 1 #     ,     if ind < 0: break #    1 ,   1  arr[ind] += direction[ind]*2 - 1 print (arr) 

Exemplo de trabalho:

A complexidade do algoritmo é $$$O (n * k ^ n)$, de memória - $$$O (n)$.

A correção desse algoritmo é comprovada por indução em $$$n$, aqui não descreverei a evidência.

No próximo post, analisaremos as tarefas para dinâmica.