Cálculo de integrais definidas: algoritmos básicos

Esta publicação descreve os métodos mais simples para calcular as integrais de funções de uma variável em um segmento, também chamadas de fórmulas em quadratura. Normalmente, esses métodos são implementados em bibliotecas matemáticas padrão, como a GNU Scientific Library para C, SciPy para Python e outros. A publicação tem como objetivo demonstrar como esses métodos funcionam "sob o capô" e chamar a atenção para alguns problemas de precisão e desempenho dos algoritmos. Eu também gostaria de observar a relação das fórmulas de quadratura e métodos de integração numérica de equações diferenciais ordinárias, sobre as quais quero escrever outra publicação.

Definição da integral

Integral (de acordo com Riemann) de uma função $$$f (x)$ no segmento $$$[a; b]$ O seguinte limite é chamado:

onde $$$\ Delta x = \ max \ lbrace x_ {i + 1} - x_i \ rbrace$ - finura da partição, $$$x_0 = a$ , $$$x_n = b$ , $$$\ xi_i$ - um número arbitrário no segmento $$$[x_i; x_ {i + 1}]$ .

Se a integral da função existir, o valor limite será o mesmo, independentemente da partição, se for suficientemente pequeno.

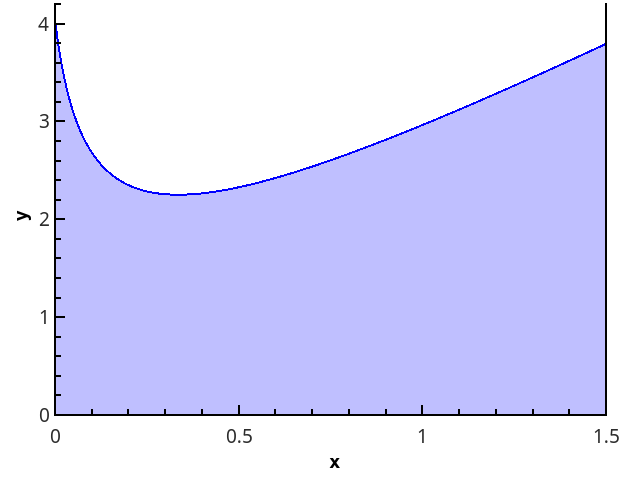
A definição geométrica é mais clara - a integral é igual à área do trapézio curvo delimitada pelo eixo 0 x , o gráfico da função e as linhas retas x = aex = b (região preenchida na figura).

Fórmulas de quadratura

A definição da integral (1) pode ser reescrita na forma

onde $$$w_i$ - coeficientes de ponderação, cuja soma deve ser igual a 1, e os próprios coeficientes - tendem a zero com número crescente $$$n$ pontos nos quais a função é calculada.

A expressão (2) é a base de todas as fórmulas de quadratura (isto é, fórmulas para o cálculo aproximado da integral). O desafio é selecionar pontos $$$\ lbrace \ xi_i \ rbrace$ e peso $$$w_i$ de modo que a soma no lado direito se aproxime da integral necessária da maneira mais precisa possível.

Tarefa computacional

Conjunto de funções $$$f (x)$ para o qual existe um algoritmo para calcular valores em qualquer ponto do intervalo $$$[a; b]$ (Refiro-me aos pontos representados por um número de ponto flutuante - não há funções Dirichlet lá!).

É necessário encontrar o valor aproximado da integral $$$\ int_a ^ b f (x) dx$ .
As soluções serão implementadas no Python 3.6.

Para verificar os métodos, use a integral $$$\ int_0 ^ {3/2} \ left [2x + \ frac {1} {\ sqrt {x + 1/16}} \ right] dx = 17/4$ .

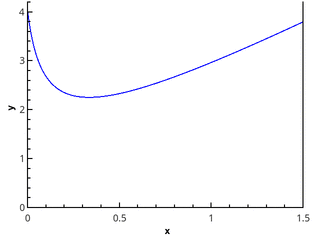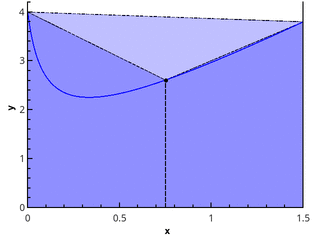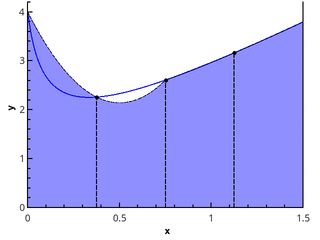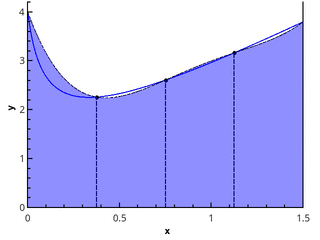
Aproximação constante por partes

As fórmulas de quadratura idealmente simples surgem da aplicação da expressão (1) "na testa":

Porque do método de dividir um segmento por pontos $$$\ lbrace x_i \ rbrace$ e selecione pontos $$$\ lbrace \ xi_i \ rbrace$ o valor limite não depende, então nós os escolhemos para que possam ser calculados convenientemente - por exemplo, tomamos a partição uniformemente e, para os pontos do cálculo da função, consideramos as opções: 1) $$$\ xi_i = x_i$ ; 2) $$$\ xi_i = x_ {i + 1}$ ; 3) $$$\ xi_i = (x_i + x_ {i + 1}) / 2$ .

Obtemos os métodos de retângulos esquerdos, retângulos direitos e retângulos com um ponto médio, respectivamente.

def _rectangle_rule(func, a, b, nseg, frac): """  .""" dx = 1.0 * (b - a) / nseg sum = 0.0 xstart = a + frac * dx # 0 <= frac <= 1    , #    , #     dx for i in range(npoints): sum += func(xstart + i * dx) return sum * dx def left_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, nseg, 0.0) def right_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, npoints, 1.0) def midpoint_rectangle_rule(func, a, b, nseg): """    """ return _rectangle_rule(func, a, b, nseg, 0.5) 

Para analisar o desempenho das fórmulas em quadratura, construímos um gráfico do erro nas coordenadas "o número de pontos é a diferença entre o resultado numérico e o exato".

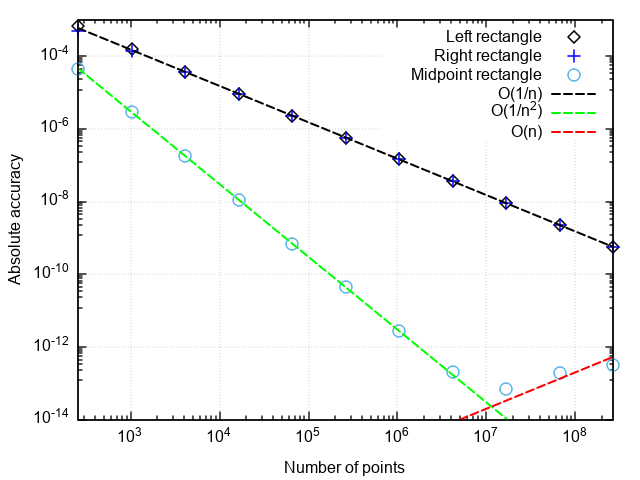
O que você pode perceber:

1. Uma fórmula com um ponto médio é muito mais precisa do que com um ponto direito ou esquerdo
2. O erro da fórmula com o ponto médio cai mais rápido que os outros dois
3. Com uma partição muito pequena, o erro da fórmula com o ponto médio começa a aumentar
   Os dois primeiros pontos estão relacionados ao fato de que a fórmula dos retângulos com um ponto médio tem uma segunda ordem de aproximação, ou seja, $$$| I_n - I | = O (1 / n ^ 2)$ , e as fórmulas dos retângulos direito e esquerdo são de primeira ordem, ou seja, $$$| I_n - I | = O (1 / n)$ .
   Um aumento no erro durante a retificação da etapa de integração está associado a um aumento no erro de arredondamento ao somar um grande número de termos. Este erro cresce como $$$| I_n - I | = O (1 / n)$ isso não permite que a integração atinja a precisão da máquina.
   Conclusão: os métodos de retângulos com pontos direito e esquerdo têm baixa precisão, o que também cresce lentamente com o refinamento da partição. Portanto, eles só fazem sentido para fins de demonstração. O método de retângulos com um ponto médio tem uma ordem de aproximação mais alta, o que lhe dá a chance de ser usado em aplicações reais (mais sobre isso abaixo).

Aproximação linear por partes

O próximo passo lógico é aproximar a função integrável em cada um dos sub-segmentos por uma função linear, que fornece a fórmula de quadratura dos trapézios:

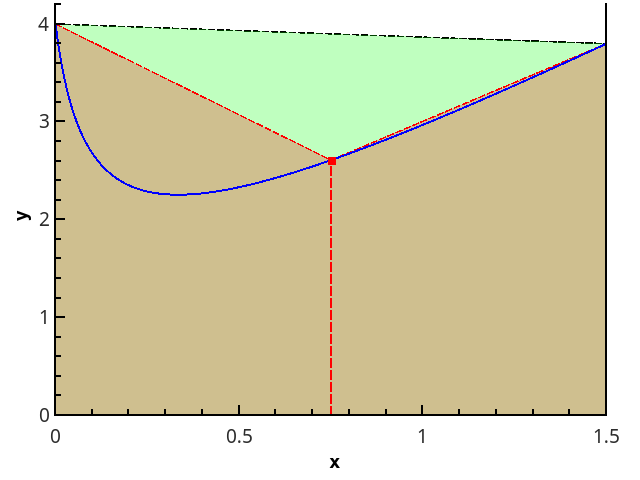
Ilustração do método trapezoidal para n = 1 en = 2.

No caso de uma grade uniforme, os comprimentos de todos os segmentos da partição são iguais e a fórmula tem a forma

 def trapezoid_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" dx = 1.0 * (b - a) / nseg sum = 0.5 * (func(a) + func(b)) for i in range(1, nseg): sum += func(a + i * dx) return sum * dx 

Tendo plotado o erro versus o número de pontos de divisão, vemos que o método trapézio também tem uma segunda ordem de aproximação e geralmente fornece resultados ligeiramente diferentes do método retângulo do ponto médio (daqui em diante simplesmente o método retângulo).

Controle de precisão de cálculo

Definir o número de pontos de divisão como um parâmetro de entrada não é muito prático, pois geralmente é necessário calcular a integral não com uma determinada densidade de divisão, mas com um determinado erro. Se o integrando é conhecido com antecedência, podemos estimar o erro com antecedência e escolher uma etapa de integração para que a precisão especificada seja certamente alcançada. Mas esse raramente é o caso na prática (e, em geral, não é mais fácil, com a função conhecida antecipadamente, integrar a integral antecipadamente?). Portanto, é necessário um procedimento para ajustar automaticamente a etapa a um determinado erro.

Como implementar isso? Um dos métodos simples para estimar o erro - a regra Runge - a diferença nos valores das integrais calculados a partir de n e 2 n pontos, fornece uma estimativa de erro: $$$\ Delta_ {2n} \ approx | I_ {2n} - I_n |$ . O método trapézio é mais conveniente para dobrar a finura de uma partição do que o método dos retângulos com um ponto central. Ao calcular pelo método trapézio, para dobrar o número de pontos, novos valores da função são necessários apenas no meio dos segmentos da partição anterior, ou seja, a aproximação anterior da integral pode ser usada para calcular a próxima.

A partir daqui, obtemos o seguinte código para o método trapezoidal com controle de precisão:

 def trapezoid_rule(func, a, b, rtol = 1e-8, nseg0 = 1): """  rtol -     nseg0 -    """ nseg = nseg0 old_ans = 0.0 dx = 1.0 * (b - a) / nseg ans = 0.5 * (func(a) + func(b)) for i in range(1, nseg): ans += func(a + i * dx) ans *= dx err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = 0.5 * (ans + midpoint_rectangle_rule(func, a, b, nseg)) #      #       nseg *= 2 err_est = abs(ans - old_ans) return ans 

Com essa abordagem, o integrando não será calculado várias vezes em um ponto e todos os valores calculados serão usados ​​para o resultado final.

Mas é possível obter maior precisão com o mesmo número de cálculos de funções? Acontece que é possível, existem fórmulas que funcionam com mais precisão do que o método trapézio na mesma grade.

Aproximação parabólica por partes

O próximo passo é aproximar a função com elementos parabólicos. Isso requer que o número de segmentos da partição seja par; então, as parábolas podem ser traçadas através de triplos de pontos com abscissas {( x ₀ = a , x ₁ , x ₂ ), ( x ₂ , x ₃ , x ₄ ), ..., ( x _{n -2} , x _{n -1} , x _n = b )}.

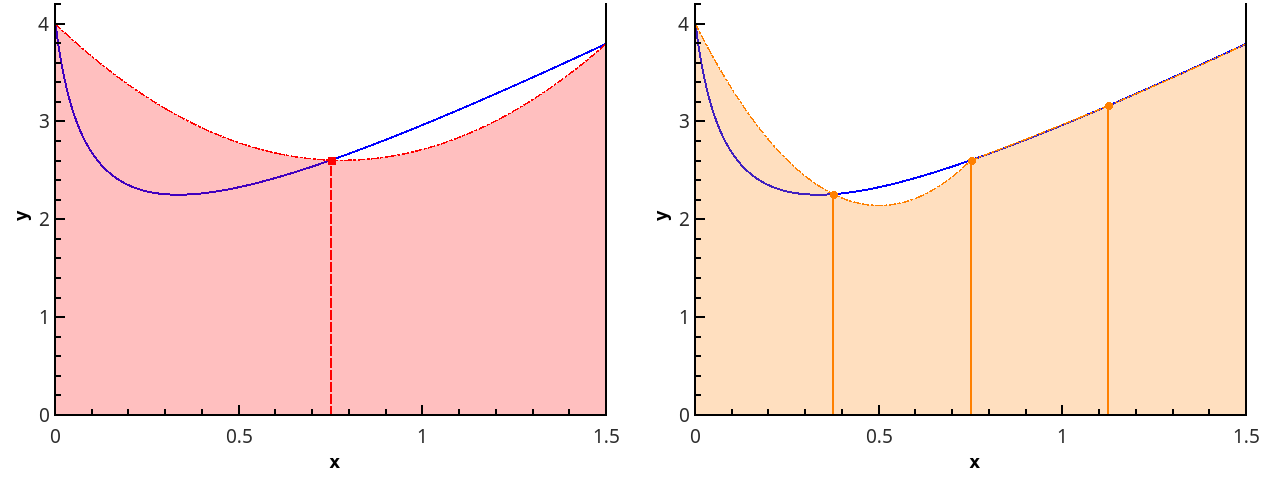
Ilustração de uma aproximação parabólica por partes em 3 e 5 pontos ( n = 2 en = 3).

Aproximando-se da integral da função em cada um dos segmentos [ x _k ; x _{k +2} ] pela integral da aproximação parabólica desse segmento e considerando os pontos uniformemente distribuídos ( x _{k +1} = x _k + h ), obtemos a fórmula de Simpson :

A fórmula (4) produz diretamente uma implementação "ingênua" do método Simpson:

 def simpson_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" if nseg%2 = 1: nseg += 1 dx = 1.0 * (b - a) / nseg sum = (func(a) + 4 * func(a + dx) + func(b)) for i in range(1, nseg / 2): sum += 2 * func(a + (2 * i) * dx) + 4 * func(a + (2 * i + 1) * dx) return sum * dx / 3 

Para estimar o erro, você pode usar o mesmo cálculo da integral com as etapas heh / 2 - mas aqui está o problema: ao calcular a integral com uma etapa menor, o resultado do cálculo anterior precisará ser descartado, embora metade dos novos cálculos de função estejam nos mesmos pontos de antes.

Felizmente, você pode evitar desperdiçar o tempo da máquina se implementar o método Simpson de uma maneira mais engenhosa. Tendo examinado mais de perto, notamos que a integral pela fórmula de Simpson pode ser representada através de duas integrais pela fórmula trapezoidal com etapas diferentes. Isso é mais claramente visto no caso básico de aproximação da integral em três pontos $$$(a, f_0), ~ (a + h, f_1), ~ (a + 2h, f_2)$ :

Assim, se implementarmos o procedimento de reduzir o passo pela metade e armazenar os dois últimos cálculos pelo método trapezoidal, o método Simpson com controle de precisão será implementado com mais eficiência.

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #           nseg0 Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def trapezoid(func, x0, x1, rtol = 1e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ ans = Quadrature.__restart(func, x0, x1, nseg0) old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = Quadrature.__double_nseg(func, x0, x1) err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans def simpson(func, x0, x1, rtol = 1.0e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ old_trapez_sum = Quadrature.__restart(func, x0, x1, nseg0) new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans old_trapez_sum = new_trapez_sum new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans 

Compare a eficácia do método trapézio e parábola:

 >>> import math >>> Quadrature.trapezoid(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 65537 4.250000001385811 >>> Quadrature.simpson(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 2049 4.2500000000490985 

Como você pode ver, com os dois métodos a resposta pode ser obtida com uma precisão bastante alta, mas o número de chamadas para o integrando é muito diferente - um método de ordem superior é 32 vezes mais eficiente!

Ao plotar o erro de integração versus o número de etapas, podemos verificar se a ordem de aproximação da fórmula de Simpson é quatro, ou seja, erro de integração numérica $$$| I_ {Simps, n} - I | = O (1 / n ^ 4)$ (e as integrais de polinômios cúbicos usando essa fórmula são calculadas até erros de arredondamento para qualquer valor igual a n > 0!).

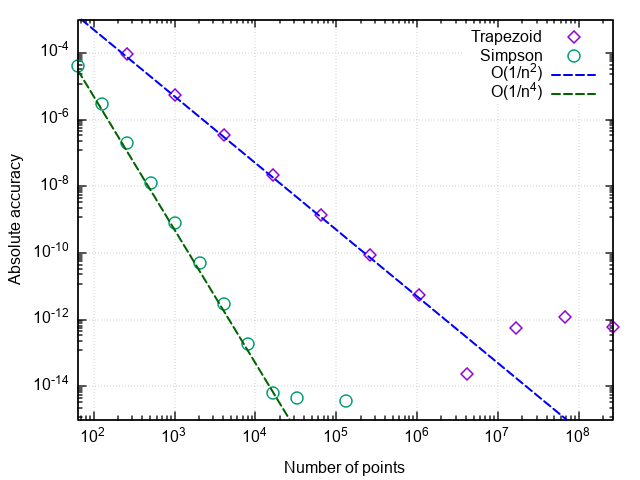
Portanto, esse aumento de eficiência surge em comparação com a fórmula trapezoidal simples.

O que vem a seguir?

A lógica adicional de aumentar a precisão das fórmulas de quadratura é geralmente compreensível - se continuarmos a aproximar a função com polinômios de um grau cada vez mais alto, a integral desses polinômios aproximará com mais precisão a integral da função original. Essa abordagem é chamada de construção de fórmulas quadráticas de Newton-Cotes . Fórmulas com até 8 ordens de aproximação são conhecidas, mas os termos alternativos aparecem entre os coeficientes de ponderação w _i em (2), e as fórmulas perdem estabilidade nos cálculos.

Vamos tentar o outro lado. O erro da fórmula da quadratura é representado como uma série de potências da etapa de integração h . Uma propriedade notável do método trapézio (e retângulos com um ponto médio!) É que, para ele, esta série consiste apenas em graus pares:

A extrapolação de Richardson é baseada em encontrar aproximações sucessivas dessa expansão: em vez de aproximar o integrando por um polinômio, a partir das aproximações calculadas da integral $$$I (h)$ é construída uma aproximação polinomial, que para h = 0 deve fornecer a melhor aproximação ao valor verdadeiro da integral.

A expansão do erro de integração em poderes pares da etapa da partição acelera acentuadamente a convergência da extrapolação, porque para aproximação da ordem 2 n , apenas n valores da integral são necessários pelo método trapezoidal.

Se assumirmos que cada termo subsequente é menor que o anterior, podemos excluir seqüencialmente graus de h , tendo aproximações integrais calculadas com etapas diferentes. Como a implementação acima nos permite dividir facilmente a partição ao meio, é conveniente considerar as fórmulas para as etapas heh / 2.

É fácil mostrar que a exceção do termo sênior do erro da fórmula trapezoidal fornecerá exatamente a fórmula Simpson:

Repetindo um procedimento semelhante para a fórmula de Simpson, obtemos:

Se você continuar, a tabela a seguir aparece:

A primeira coluna contém as integrais calculadas pelo método trapezoidal. Ao mover da linha superior para baixo, a divisão do segmento se torna duas vezes menor e, ao mover da coluna esquerda para a direita, a ordem de aproximação da integral aumenta (ou seja, a segunda coluna contém as integrais pelo método Simpson, etc.).

Os elementos da tabela, como pode ser deduzido da expansão (5), são relacionados pela relação de recorrência:

O erro da aproximação da integral pode ser estimado a partir da diferença de fórmulas de ordens diferentes em uma linha, ou seja,

O uso da extrapolação de Richardson juntamente com a integração trapezoidal é chamado de método de Romberg . Se o método Simpson leva em conta os dois valores anteriores pelo método trapezoidal, o método Romberg usa todos os valores previamente calculados pelo método trapezoidal para obter uma estimativa mais precisa da integral.

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #          nseg0  Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def romberg(func, x0, x1, rtol = 1e-10, nseg0 = 1, maxcol = 5, reset_calls = True): """   nseg0 -     maxcol -   """ #   Itable = [[Quadrature.__restart(func, x0, x1, nseg0, reset_calls)]] i = 0 maxcol = max(0, maxcol) ans = Itable[i][i] error_est = max(1, abs(ans)) while (error_est > abs(rtol * ans)): old_ans = ans i += 1 d = 4.0 ans_col = min(i, maxcol) Itable.append([Quadrature.__double_nseg(func, x0, x1)] * (ans_col + 1)) for j in range(0, ans_col): diff = Itable[i][j] - Itable[i - 1][j] Itable[i][j + 1] = Itable[i][j] + diff / (d - 1.0) d *= 4.0 ans = Itable[i][ans_col] if (maxcol <= 1): #       error_est = abs(ans - Itable[i - 1][-1]) elif (i > maxcol): error_est = abs(ans - Itable[i][min(i - maxcol - 1, maxcol - 1)]) else: error_est = abs(ans - Itable[i - 1][i - 1]) print("Total function calls: " + str(Quadrature.__ncalls)) return ans 

Vamos verificar como funciona a aproximação de alta ordem:

 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 0) #  Total function calls: 65537 4.250000001385811 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 1) #  Total function calls: 2049 4.2500000000490985 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 4) Total function calls: 257 4.250000001644076 

Estamos convencidos de que, em comparação com o método da parábola, o número de chamadas para o integrando diminuiu mais 8 vezes. Com um aumento adicional na precisão necessária, as vantagens do método Romberg se tornam ainda mais pronunciadas:

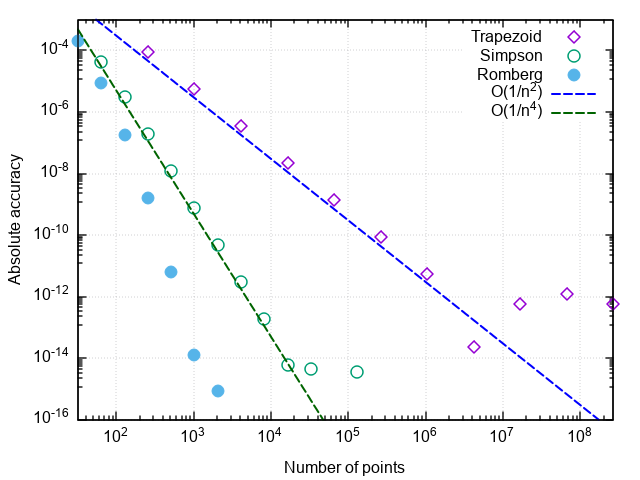
Algumas notas

Observação 1. O número de chamadas de função nesses problemas caracteriza o número de somas ao calcular a integral. Reduzir o número de cálculos do integrando não apenas economiza recursos de computação (embora também seja o caso de uma implementação mais otimizada), mas também reduz o efeito de erros de arredondamento no resultado. Portanto, ao tentar calcular a integral da função de teste, o método trapézio congela ao tentar obter uma precisão relativa de 5 × 10 ^-15 , o método da parábola - com a precisão desejada de 2 × 10 ^-16 (que é o limite para números de precisão dupla), e o método Romberg lida com o cálculo teste integral até a precisão da máquina (com um erro de bit baixo). Ou seja, não apenas a precisão da integração é aumentada para um determinado número de chamadas de função, mas também a precisão máxima alcançável do cálculo da integral.

Observação 2. Se o método convergir quando uma certa precisão for especificada, isso não significa que o valor calculado da integral tenha a mesma precisão. Antes de tudo, isso se aplica aos casos em que o erro especificado está próximo da precisão da máquina.

Observação 3. Embora o método de Romberg para várias funções funcione de maneira quase mágica, ele assume que o integrando limitou derivadas de ordens superiores. Isso significa que, para funções com dobras ou quebras, pode ser pior do que métodos simples. Por exemplo, integre f ( x ) = | x |:

 >>> Quadrature.trapezoid(abs, -1, 3, rtol=1e-5) Total function calls: 9 5.0 >>> Quadrature.simpson(abs, -1, 3, rtol=1e-5) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 2) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 3) Total function calls: 33 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 4) Total function calls: 33 5.000001383269357 

Observação 4. Pode parecer que quanto maior a ordem de aproximação, melhor. De fato, é melhor limitar o número de colunas na tabela Romberg para 4-6. Para entender isso, veja a fórmula (6). O segundo termo é a diferença de dois elementos consecutivos da coluna j -1, divididos por cerca de 4 ^j . Porque a j- ésima coluna contém aproximações de uma integral de ordem 2 j , então a diferença em si é da ordem de (1 / n _i ) ^{2 j} ~ 4 ^{- ij} . Considerando a divisão, obtém-se ~ 4 ^{- ( i +1) j} ~ 4 ^{- j 2} . I.e. para j ~ 7, o segundo termo em (6) perde precisão após a redução das ordens ao adicionar números de ponto flutuante, e um aumento na ordem de aproximação pode levar ao acúmulo de erros de arredondamento.

Observação 5. As partes interessadas podem usar os métodos descritos para encontrar a integral por uma questão de interesse. $$$\ int_0 ^ 1 \ sqrt {x} \ sin {x} dx$ e equivalente a ele $$$\ int_0 ^ 1 2t ^ 2 \ sin {t ^ 2} dt$ . Como se costuma dizer, sinta a diferença.

Conclusão

É apresentada a descrição e implementação dos métodos básicos de integração numérica de funções em uma grade uniforme. Demonstra-se como, usando uma modificação simples, obter a classe de fórmulas de quadratura usando o método de Romberg com base no método trapezoidal, o que acelera significativamente a convergência da integração numérica. O método funciona bem para integrar funções "comuns", isto é, variação fraca no intervalo de integração, sem singularidades nas bordas do segmento (ver observação 5), oscilações rápidas etc.

( [3] — C++).

1. .. , .. . . .: . 1989.
2. J. Stoer, R. Bulirsch. Introduction to Numerical Analysis: Second Edition. Springer-Verlag New York. 1993.
3. WH Press, SA Teukolsky, WT Vetterling, BP Flannery. Numerical Recipes: Third Edition. Cambridge University Press. 2007.