Na Índia, existe um análogo local do nosso INN - "adhar". O sistema eletrônico "eAdhar" está preso a ele. No eAdhara, cada letra é bloqueada com uma senha. E tudo ficaria bem, mas a senha é composta de acordo com um padrão simples: as quatro primeiras letras do nome são maiúsculas e o ano de nascimento.
Quatro letras maiúsculas e quatro números. Destas, 2.821.109.909.456 combinações podem ser compiladas. Se você marcar mil combinações por segundo, uma senha levará noventa anos.
Muito tempo. Podemos acelerar algumas ( bilhões ) vezes?
92 anos → 52 dias. Grupo
Com três trilhões de combinações, tivemos um pouco mais. Ainda assim, o modelo é conhecido:
([AZ][AZ][AZ][AZ]) ([0–9][0–9][0–9][0–9]) (4 ) (4 ) ( 1) ( 2)
Dado esse padrão, linhas como S2N65GE1 podem ser descartadas imediatamente. Quantas combinações você obtém então?
O primeiro grupo tem quatro caracteres alfabéticos. 26 opções, 4 posições, temos:
4 posições de 10 dígitos, da mesma forma:
A partir disso, obtemos o número total de combinações:
Vamos estimar quanto de força bruta será mais rápida agora. Novamente, procedemos de 1000 tentativas por segundo:
Ou 52 dias, 21 horas, 22 minutos e 40 segundos. Em vez de 92 anos. Nada mal. Mas ainda há muito tempo. O que mais pode ser feito? A mesma coisa - reduza o número de combinações.
52 dias → 12 horas. Ativar o senso comum
O primeiro e o segundo grupo não são um conjunto aleatório de caracteres, mas as primeiras letras do nome e ano de nascimento. Vamos começar com o ano de nascimento.
Não faz sentido selecionar senhas para os nascidos em 1642 ou 2594. Portanto, o intervalo de combinações pode ser reduzido com segurança de 0000–9999 a 1918–2018. Portanto, cobriremos o mais ou menos de todos os que vivem com 0 a 100 anos de idade. Graças a isso, o número de combinações e o tempo são reduzidos, respectivamente:
Ou 12 horas, 41 minutos e 37 segundos.
12 horas → 2 minutos. Sacrificamos a precisão
12 horas é ótimo, mas ... Precisamos ir mais fundo .
Agora, temos 45 milhões de combinações que cobrem com precisão todos os usuários do eAdhara. Mas e se sacrificar uma pequena fração para aumentar a velocidade?
Aperfeiçoamos as combinações digitais. Cartas fazem algo semelhante. A lógica é simples: não há ano de nascimento 9999 e, da mesma forma, não há nome indiano com "AAAA" no início. Mas como determinar todas as combinações adequadas?
Eu coletei nomes indianos no site do catálogo, o Photon me ajudou muito nisso. O resultado são 3.283 nomes exclusivos. Resta aparar as quatro primeiras letras e remover duplicatas:
grep -oP ”^\w{4}” custom.txt | sort | uniq | dd conv=ucase
Descobriram 1.598 prefixos! Havia algumas duplicatas, porque as quatro primeiras letras em nomes como "Sanjeev" e "Sanjit" são as mesmas.
1.598 prefixos - insuficientes para um bilhão e meio de pessoas? Eu concordo Mas não esqueça que estes são prefixos, não nomes. Publiquei a lista resultante no Gist . De fato, deveria haver mais. Você pode ficar confuso, coletar 10.000 nomes de outros sites e obter 3.000 prefixos exclusivos, mas não tive tempo para isso. Então, vamos começar a partir de 1.598.
Vamos calcular quanto tempo é necessário agora:
Ou 2 minutos e 39,8 segundos.
2 minutos → 2 segundos. Wikipedia para o resgate
2 minutos e 40 segundos é o tempo necessário para classificar todas as combinações. Mas e se a décima primeira combinação estiver correta? Ou o último? Ou o primeiro?
Agora a lista de combinações é classificada em ordem alfabética. Mas isso não faz sentido - quem disse que os nomes em "A" são mais comuns que em "B" ou que há mais crianças de um ano do que as de setenta?
É necessário considerar a probabilidade de cada combinação. Na Wikipedia, eles escrevem:
Na Índia, mais de 50% da população tem menos de 25 anos e mais de 65% tem menos de 35 anos.
Com base nisso, em vez da lista 1–100, você pode tentar o seguinte:
25–01 ( , , ) 25–35 36–100
Então acontece que a probabilidade do primeiro combinações aumenta para 50%. Quebramos metade das senhas para segundos! No seguinte segundos, pegaremos outros 15% de senhas. Total - 65% das senhas em 55,9 segundos.
Agora para os nomes.
No Google, é fácil encontrar os 100 melhores nomes de qualquer país. Com base nos dados da Índia, movi as combinações apropriadas para o topo da lista. Assumimos que 15% da população da Índia tenha nomes populares. Portanto, 15% das senhas podem ser quebradas quase instantaneamente.
Hindus - 80% da população da Índia. Portanto, se você colocar os nomes hindus acima na lista, ele acelerará 80% das tentativas. Após o passo anterior, deixamos 
tentativas. Se 80% deles são nomes hindus, então 79% (deixamos 1% para nomes populares, mas não hindus), quebraremos nos próximos 65% das tentativas.
Vamos contar tudo juntos, levando em consideração as estatísticas de idade. Divida em grupos:
100: { 50: 00 25 { 7: , 43: { 34: , 9: } } 15: 26 35 { 3: , 13*: { 10: , 3: } } 45: 36 100 { 7: , 38: { 30: , 8: } } }
Agora vamos criar um algoritmo eficiente para quebrar senhas:
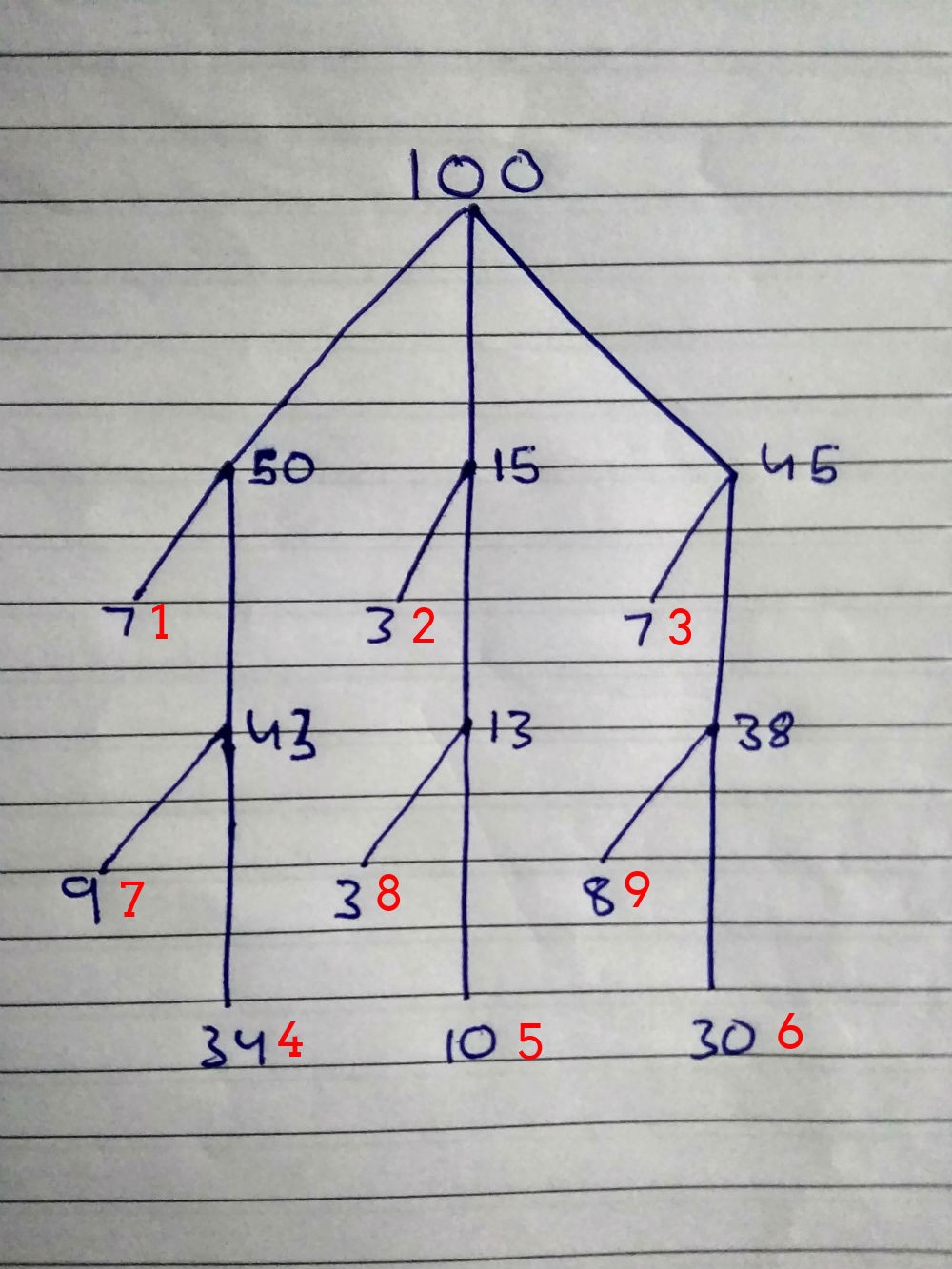
Números vermelhos são uma prioridade de pesquisa. As combinações para as pessoas do primeiro grupo são testadas primeiro, depois segundo, depois terceiro e assim por diante.
Quanto tempo leva para hackear agora?
Fase 1
1 = 11 segundos para decifrar 7 senhas
2 = 3 segundos para quebrar 3 senhas
3 = 11 segundos para quebrar 7 senhas
Deciframos as senhas de 17 pessoas, restando 83. Removeremos as combinações anteriores da lista e tentaremos os seguintes conjuntos - 4, 5, 6.
Fase 2
4 = 54 segundos para decifrar 34 senhas
5 = 16 segundos para decifrar 10 senhas
6 = 47 segundos para decifrar 30 senhas
Mais uma vez, exclua as combinações das fases anteriores.
Fase 3
7 = 14 segundos para quebrar 9 senhas
8 = 5 segundos para decifrar 3 senhas
9 = 12 segundos para decifrar 8 senhas
Tempo total : segundos ou 2 minutos e 13 segundos.
Senhas quebradas : 100
Tempo médio para uma senha : segundos.
92 anos → 1,73 segundos. Nitsche então, certo?