Prepare-se, você encontrará um artigo extremamente pedante, o que pode poupar uma entrevista ou economizar algumas horas enquanto captura um bug na produção!

Estou trabalhando ativamente na segunda temporada do The Impostor's Guide e estou escrevendo sobre o código RSA para SSH, que obviamente é o código mais baixado da história da TI.

Eu gostaria de entender completamente essa história. Quem inventou esse código, como funciona, por que funciona e se funcionará no futuro . Agora, descobri uma história muito interessante . Eu não sou um criptomaníaco e vejo outros literalmente sugando essa área. Mas também estou interessado nisso, porque há pequenos visons em todos os lugares e, como pegas, sou atraído por coisas brilhantes em visons profundos . Eu também sou muito bom em metáforas.

De qualquer forma: na semana passada eu aprendi algo estranho e quero compartilhar: acontece que mod e o restante da divisão não são a mesma coisa . É realmente engraçado que alguns leitores pulem de seus lugares e gritem com estas palavras: "Mas é exatamente isso que eu sempre tentei dizer a você e a todos os outros!"

Chame os caras da seita "mod não é o resto"! Isto é para você.

O que é mod?

Eu tive que estudar isso, assim como a última vez que esse tópico apareceu. Essa é uma daquelas coisas que você sabe, mas não se lembra. Quando você usa mod, divida um número por outro e pegue o restante. Portanto: 5 mod 2 será 1, porque 5/2 = 2 com o restante de 1.

O termo mod significa operação do módulo , com o módulo 2 neste caso. A maioria das linguagens de programação usa % para indicar essa operação: 5 % 2 = 1 .

É aí que entramos na estranha área cinzenta.

A matemática do mostrador

Lembro-me de como ensinei isso na escola e depois esqueci. Existe um tipo de matemática chamada "aritmética modular" que lida com estruturas cíclicas. A maneira mais fácil de imaginar isso é um mostrador com o ciclo 12. Para um matemático, o mostrador é o mod 12 . Se você deseja entender se é possível dividir uniformemente 253 horas em dias, você pode aplicar a operação 253 mod 24 , o resultado será 13 , então a resposta é não! Podemos responder sim apenas se o resultado for 0.

Outra pergunta que você pode fazer é: "Se eu sair às 18h, que horas serão na chegada em 16 horas?" Isso será 6 + 16 mod 12 , ou seja, 10.

Os criptografadores adoram mod , porque quando usados ​​com números realmente grandes, você pode criar algo conhecido como "funções de mão única". Essas são funções especiais que facilitam o cálculo de algo em uma direção, mas não na oposta.

Se eu lhe disser que 9 é o resultado da quadratura, você pode facilmente determinar qual foi a entrada 3. Antes de ver todo o processo do início ao fim. Se eu disser que 9 é o resultado do mod 29 , será mais difícil entender qual é a entrada.

Os criptografadores gostam dessa idéia porque podem usar a divisão restante com números primos gigantes para gerar chaves criptográficas. Esta é uma história completamente diferente: se você quiser ler sobre isso, pode comprar um livro ou, melhor ainda, apoiar meus esforços para escrevê-lo .

No entanto, não nos desviaremos do tópico.

Restos e matemática do mostrador

Agora vamos direto ao ponto: módulo e o restante simples são os mesmos quando os números são positivos, mas diferem no caso de números negativos.

Considere a seguinte tarefa:

 const x = 19 % 12; console.log(x); 

Qual é o valor de x ? Divida os números e obtenha 7 como o restante de 12. Esta é a resposta correta. Que tal isso:

 const y = 19 % -12; console.log(y); 

Usando matemática comum, podemos multiplicar -12 por -1, o que dá 12, e ainda temos 7 restantes, então nossa resposta é novamente 7.

JavaScript concorda com isso:



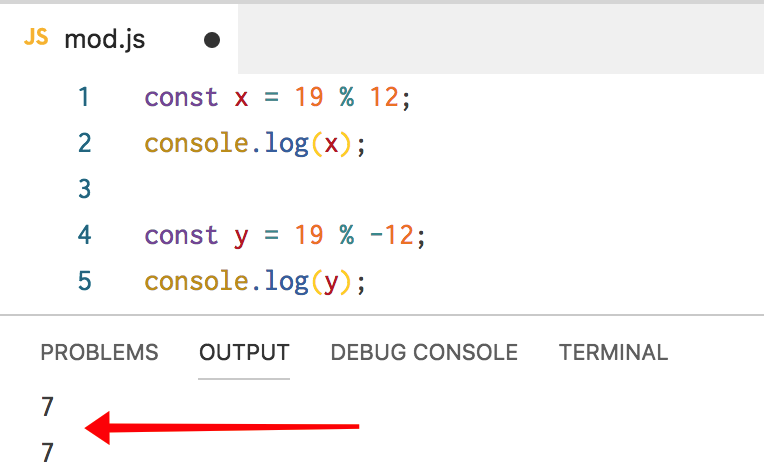
C # também concorda:



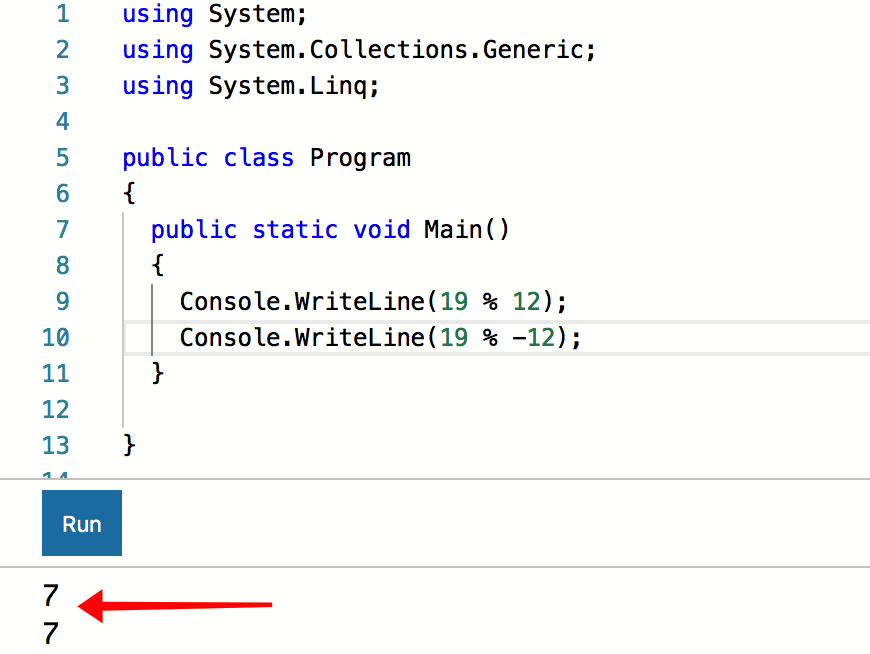
O Google concorda com a primeira declaração, mas discorda da segunda:



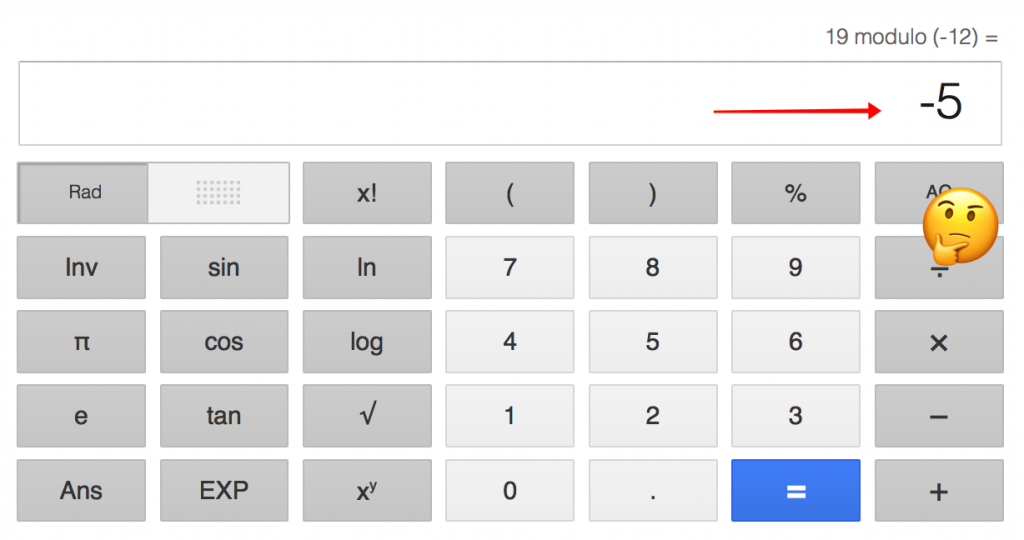
Ruby concorda com o Google:



Em nome de Dijkstra, o que está acontecendo aqui?

Há horas

Para responder à pergunta, você precisa entender a diferença entre o restante e o módulo . Os programadores combinam essas operações , mas não devem fazer isso, porque fornecem o mesmo resultado apenas se o divisor (no nosso caso 12) for positivo. Você pode enviar facilmente erros para produção se o divisor for negativo.

Mas por que há uma diferença? Considere o divisor positivo 19 mod 12 no relógio:



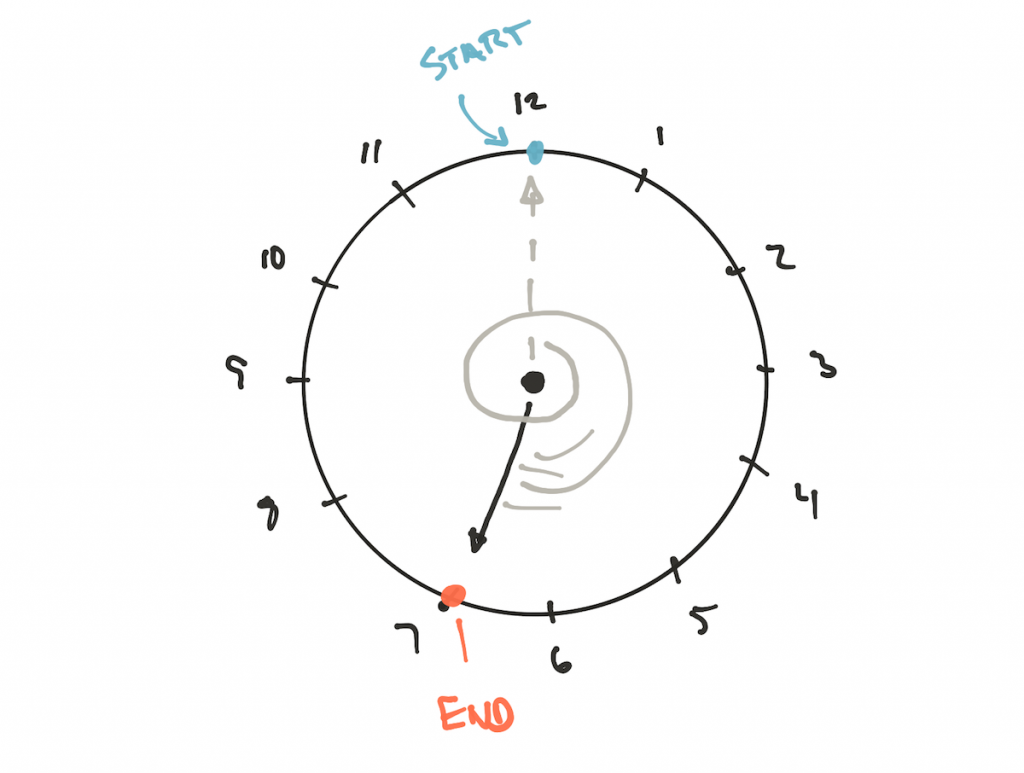
Resultado final 7. Sabemos disso e podemos provar matematicamente. Mas e quanto a 19 mod -12 ? Aqui você precisa usar outros relógios :



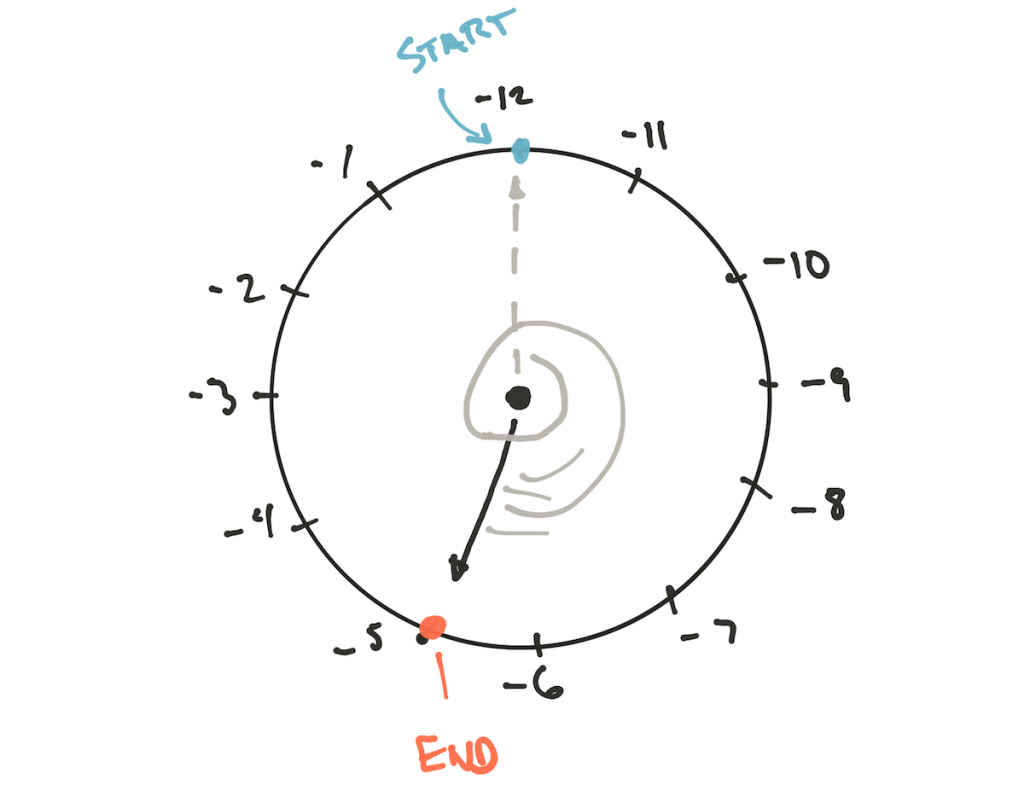
O módulo é -12 e não podemos ignorá-lo ou alterá-lo multiplicando por -1, pois a aritmética modular não funciona dessa maneira. A única maneira de calcular corretamente o resultado é reorganizar as marcas no relógio, para que passemos de -12 ou giremos o relógio no sentido anti-horário, o que dá o mesmo resultado.

Por que não iniciar tags com -1, passando para -2 etc.? Porque neste caso, voltaremos e reduziremos constantemente o resultado até atingirmos -12, e neste momento faremos um salto de +12, e o módulo não funciona assim.

Isso é uma coisa famosa.

Antes de me chamar de louca e começar a pesquisar um tópico no Google: esse é um fato bem conhecido . De fato, o MDN (Mozilla Developer Network) chegou a chamar % da operação restante, não o módulo:

O operador restante retorna o restante da divisão de um operando por outro. Ele sempre aceita o sinal do dividendo .

Aqui está o que Eric Lippert, um dos deuses do C #, diz sobre o módulo em C # :

No entanto, isso não é exatamente o que o operador% realmente faz em C #. O operador% não é um operador de módulo canônico, é um operador restante.

E o seu idioma?

E daí?

Entendo se você leu até aqui e agora coça a cabeça e se pergunta se vale a pena se preocupar. Eu acho que custa por duas razões:

1. Eu posso imaginar como essa pergunta me pegará de surpresa em uma entrevista.
2. Eu posso imaginar como esse entra em produção, e os desenvolvedores descobrirão por várias horas por que a matemática não funciona.

Esse também é um fato divertido, caso seu amigo programador pedante apareça.