Um método universal para classificar informações complexas foi descoberto

Ao abrir seu café, você gostaria de saber a resposta para a seguinte pergunta: "onde está o outro café mais próximo deste ponto?" Esta informação ajudaria você a entender melhor seus concorrentes.

Este é um exemplo do problema de pesquisa do " vizinho mais próximo ", amplamente estudado em ciência da computação. Dado um conjunto de informações e um novo ponto, e você precisa descobrir qual ponto dos existentes será o mais próximo? Essa pergunta surge em muitas situações cotidianas em áreas como pesquisa de genoma, pesquisa de imagens e recomendações do Spotify.

Mas, diferentemente do exemplo do café, as perguntas sobre o vizinho mais próximo costumam ser muito complicadas. Nas últimas décadas, as maiores mentes entre os cientistas da computação começaram a encontrar as melhores maneiras de resolver esse problema. Em particular, eles tentaram lidar com as complicações decorrentes do fato de que em diferentes conjuntos de dados pode haver definições muito diferentes da "proximidade" dos pontos entre si.

E agora, uma equipe de cientistas da computação criou uma maneira completamente nova de resolver o problema de encontrar o vizinho mais próximo. Em um par de artigos, cinco cientistas descreveram em detalhes o primeiro método generalizado para resolver o problema de encontrar o vizinho mais próximo para dados complexos.

"Este é o primeiro resultado em uma ampla gama de espaços usando uma única técnica algorítmica", disse Peter Indik , especialista em TI do Instituto de Tecnologia de Massachusetts, uma figura influente no campo dos desenvolvimentos relacionados a essa tarefa.

Diferença de distância

Estamos tão apegados à única maneira de determinar a distância que é fácil perder de vista a possibilidade de outras maneiras. Normalmente medimos a distância como euclidiana - como uma linha reta entre dois pontos. No entanto, existem situações em que outras definições fazem mais sentido. Por exemplo, a distância de Manhattan faz você girar 90 graus, como se estivesse se movendo ao longo de uma rede retangular de estradas. Para medir uma distância que pode ser de 5 quilômetros em uma linha reta, talvez seja necessário atravessar a cidade 3 km em uma direção e mais 4 na outra.

Também é possível falar sobre distâncias não no sentido geográfico. Qual é a distância entre duas pessoas em uma rede social, ou dois filmes ou dois genomas? Nestes exemplos, a distância indica o grau de similaridade.

Existem dezenas de métricas de distância, cada uma adequada para uma tarefa específica. Tomemos, por exemplo, dois genomas. Os biólogos os comparam usando a " distância de Levenshtein " ou a distância de edição. A distância de edição entre duas seqüências de genoma é o número de adições, exclusões, inserções e substituições necessárias para transformar uma delas em outra.

A distância de edição e a distância euclidiana são dois conceitos diferentes de distância, e é impossível reduzir um ao outro. Essa incompatibilidade existe para muitos pares de métricas de distância e é um obstáculo para os cientistas da computação que tentam desenvolver algoritmos para encontrar o vizinho mais próximo. Isso significa que um algoritmo que funciona para um tipo de distância não funcionará para outro - mais precisamente, até agora, até que um novo tipo de pesquisa apareceu.


Alexander Andoni

Círculo ao quadrado

A abordagem padrão para encontrar o vizinho mais próximo é dividir os dados existentes em subgrupos. Se, por exemplo, seus dados descreverem a localização das vacas no pasto, você poderá colocar cada uma delas em um círculo. Em seguida, colocamos uma nova vaca no pasto e fazemos a pergunta: em qual dos círculos ela se encaixa? É praticamente garantido que o vizinho mais próximo da nova vaca estará no mesmo círculo.

Então repita o processo. Divida os círculos em subcírculos, divida ainda mais essas células e assim por diante. Como resultado, há uma célula com apenas dois pontos: o existente e o novo. Este ponto existente será o seu vizinho mais próximo.


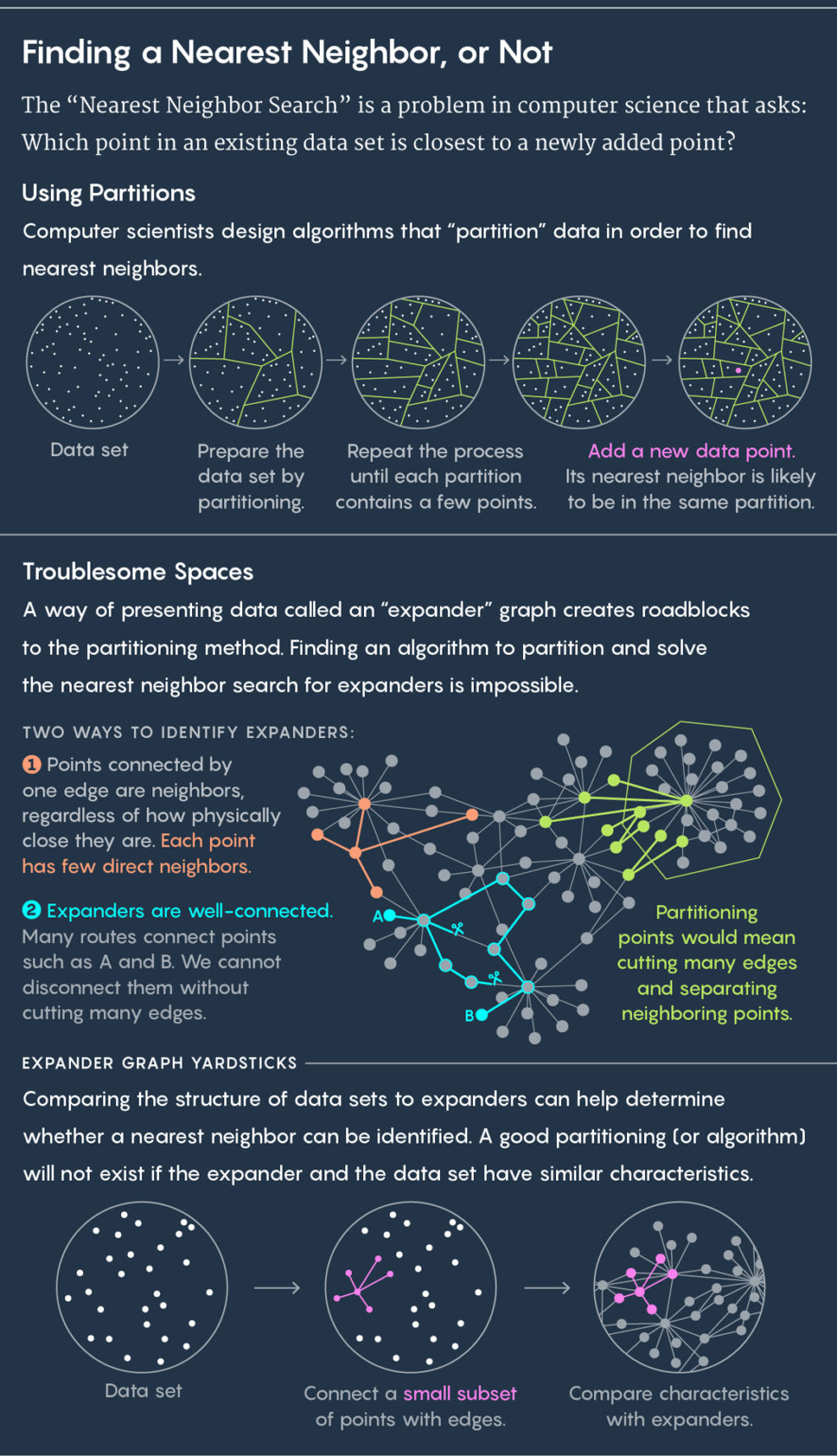Acima está a divisão dos dados em células. Abaixo está o uso do gráfico de extensão.

Os algoritmos desenham células, bons algoritmos desenham-nas rápida e bem - isto é, para que não haja situação em que uma nova vaca caia em um círculo e seu vizinho mais próximo termine em outro círculo. "Queremos que os pontos próximos nessas células apareçam com mais frequência na mesma unidade e os distantes sejam raros", disse Ilya Razenshtein , especialista em ciência da computação da Microsoft Research, coautora do novo trabalho, que também envolveu Alexander Andoni, da Columbia University , Assaf Naor, de Princeton, Alexander Nikolov, da Universidade de Toronto, e Eric Weingarten, da Columbia University.

Por muitos anos, os cientistas da computação criaram vários algoritmos para desenhar essas células. Para dados pequenos - como onde um ponto é determinado por um pequeno número de valores, por exemplo, a localização de uma vaca em um pasto - algoritmos criam o chamado " Diagramas de Voronoi " que respondem com precisão à pergunta sobre o vizinho mais próximo.

Para dados multidimensionais, nos quais um ponto pode ser determinado por centenas ou milhares de valores, os diagramas de Voronoi exigem muito poder de computação. Em vez disso, os programadores desenham células usando " hash localmente sensível " , descrito pela primeira vez por Indik e Rajiv Motwani em 1998. Os algoritmos LF desenham células aleatoriamente. Portanto, eles trabalham mais rápido, mas com menos precisão - em vez de encontrar o vizinho mais próximo exato, garantem que um ponto esteja localizado a não mais do que uma determinada distância do vizinho real mais próximo. Isso pode ser imaginado como uma recomendação de filme da Netflix, que não é perfeita, mas é boa o suficiente.

Desde o final dos anos 90, os cientistas da computação criaram algoritmos LF que fornecem soluções aproximadas para a tarefa de encontrar o vizinho mais próximo para determinadas métricas de distância. Os algoritmos eram muito especializados e o algoritmo desenvolvido para uma métrica de distância não poderia ser usado para outra.

“Você pode criar um algoritmo muito eficaz para a distância euclidiana ou Manhattan, para alguns casos específicos. Mas não tínhamos um algoritmo que funcionasse em uma grande classe de distâncias ", disse Indik.

Como os algoritmos que trabalham com uma métrica não podem ser usados ​​para outra, os programadores criaram uma estratégia de solução alternativa. Por meio de um processo chamado "incorporação", eles impuseram uma métrica, para a qual não possuíam um bom algoritmo, na métrica para a qual era. No entanto, a correspondência das métricas era geralmente imprecisa - algo como uma estaca quadrada em um buraco redondo. Em alguns casos, a incorporação não funcionou. Era necessário criar uma maneira universal de responder à pergunta sobre o vizinho mais próximo.


Ilya Razenshtein

Resultado inesperado

Em um novo trabalho, os cientistas abandonaram a busca por algoritmos especiais. Em vez disso, eles fizeram uma pergunta mais ampla: o que impede o desenvolvimento de um algoritmo em uma determinada métrica de distância?

Eles decidiram que a situação desagradável associada ao gráfico em expansão, ou expansor , era responsável. Um expansor é um tipo especial de gráfico, um conjunto de pontos conectados por arestas. Os gráficos têm sua própria métrica de distância. A distância entre dois pontos do gráfico é o número mínimo de linhas necessárias para ir de um ponto a outro. Você pode imaginar um gráfico representando as conexões entre as pessoas nas redes sociais e, em seguida, a distância entre as pessoas será igual ao número de conexões que as separam. Se, por exemplo, Julian Moore tem um amigo que tem Kevin Bacon como amigo, então a distância de Moore para Bacon é três.

Um expansor é um tipo especial de gráfico que possui duas propriedades conflitantes à primeira vista. Possui alta conectividade, ou seja, dois pontos não podem ser desconectados sem cortar várias arestas. Ao mesmo tempo, a maioria dos pontos está conectada a um número muito pequeno de outros. Por isso, a maioria dos pontos está longe um do outro.

Uma combinação única dessas propriedades - boa conectividade e um pequeno número de arestas - leva ao fato de que nos expansores é impossível realizar uma pesquisa rápida pelo vizinho mais próximo. Qualquer tentativa de dividi-lo em células separará pontos próximos uns dos outros.

"Qualquer maneira de cortar o expansor em duas partes exige o corte de várias nervuras, o que divide muitos vértices espaçados", disse Weingarten, co-autor do trabalho.

No verão de 2016, Andoni, Nyokolov, Rasenstein e Vanguarten sabiam que para os expansores não era possível criar um bom algoritmo para encontrar o vizinho mais próximo. Mas eles queriam provar que é impossível construir tais algoritmos para muitas outras métricas de distância - métricas, ao procurar bons algoritmos para os quais os cientistas da computação pararam.

Para encontrar evidências da impossibilidade de tais algoritmos, eles precisavam encontrar uma maneira de incorporar a métrica do expansor em outras métricas de distância. Com esse método, eles podem determinar que outras métricas têm propriedades semelhantes às propriedades do expansor, o que as impede de criar bons algoritmos.


Eric Weingarten

Quatro cientistas da computação foram para Assaf Naoru, um matemático da Universidade de Princeton, cujo trabalho anterior era bem adequado ao tópico dos expansores. Eles pediram que ele ajudasse a provar que os expansores podem ser incorporados em vários tipos de métricas. Naor voltou rapidamente com uma resposta - mas não a que eles esperavam dele.

"Pedimos a Assaf que nos ajudasse com essa afirmação, e ele provou o contrário", disse Andoni.

Naor provou que os expansores não se enquadram em uma grande classe de métricas de distância conhecidas como " espaços normatizados " (que também inclui métricas como espaços euclidianos e Manhattan). Com base nas evidências de Naor, os cientistas seguiram a seguinte cadeia lógica: se os expansores não se ajustarem à métrica da distância, deve haver uma boa maneira de quebrá-los em células (uma vez que, como provaram, as propriedades dos expansores são o único obstáculo para isso). Portanto, deve haver um bom algoritmo para encontrar o vizinho mais próximo - mesmo que ninguém ainda o tenha encontrado.

Cinco pesquisadores publicaram suas descobertas em um artigo concluído em novembro e enviado em abril. Foi seguido por um segundo trabalho, que foram concluídos este ano e publicados em agosto. Nele, eles usaram as informações obtidas ao escrever o primeiro trabalho para encontrar um algoritmo rápido para encontrar o vizinho mais próximo para espaços normatizados.

"O primeiro trabalho demonstrou a existência de uma maneira de dividir a métrica em duas partes, mas não havia receita para fazê-lo rapidamente", disse Weingarten. "No segundo trabalho, argumentamos que existe uma maneira de separar os pontos e, além disso, que essa separação pode ser feita usando algoritmos rápidos".

Como resultado, novos trabalhos, pela primeira vez, generalizam a busca pelo vizinho mais próximo em dados multidimensionais. Em vez de desenvolver algoritmos especializados para métricas específicas, os programadores têm uma abordagem universal para encontrar algoritmos.

"Este é um método ordenado para o desenvolvimento de algoritmos para encontrar o vizinho mais próximo em qualquer uma das métricas de distância necessárias", disse Weingarten.