
Agora todo mundo está falando muito sobre inteligência artificial e sua aplicação em todas as áreas da empresa. No entanto, existem algumas áreas onde, desde os tempos antigos, um tipo de modelo dominava, a chamada “caixa branca” - regressão logística. Uma dessas áreas é a pontuação de crédito bancário.
Existem várias razões para isso:
- Os coeficientes de regressão podem ser facilmente explicados, diferentemente das caixas-pretas como reforço, que podem incluir mais de 500 variáveis
- O aprendizado de máquina ainda não é confiável pela gerência devido à dificuldade em interpretar modelos
- Existem requisitos não escritos do regulador para a interpretabilidade dos modelos: a qualquer momento, por exemplo, o Banco Central pode pedir uma explicação - por que um empréstimo ao mutuário foi recusado
- As empresas usam programas externos de mineração de dados (por exemplo, minerador rápido, SAS Enterprise Miner, STATISTICA ou qualquer outro pacote) que permitem aprender rapidamente como criar modelos, mesmo sem habilidades de programação
Esses motivos tornam quase impossível o uso de modelos complexos de aprendizado de máquina em algumas áreas, por isso é importante poder “extrair o máximo” de uma regressão logística simples, fácil de explicar e interpretar.
Neste post, falaremos sobre como, ao criar a pontuação, abandonamos os pacotes externos de mineração de dados em favor de soluções de código aberto na forma de Python, aumentamos a velocidade de desenvolvimento várias vezes e também melhoramos a qualidade de todos os modelos.
Processo de pontuação
O processo clássico de construção de modelos de pontuação na regressão é assim:
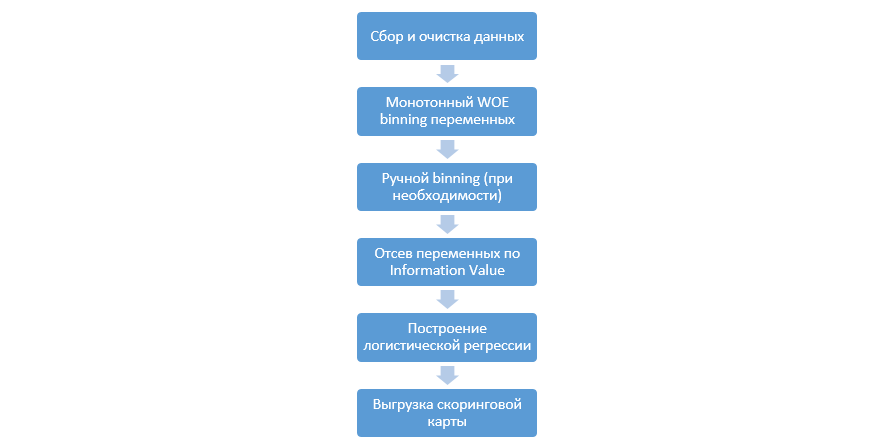
Pode variar de empresa para empresa, mas os principais estágios permanecem constantes. Sempre precisamos executar binning de variáveis (em contraste com o paradigma de aprendizado de máquina, onde na maioria dos casos apenas é necessária codificação categórica), sua triagem por Information Value (IV) e o upload manual de todos os coeficientes e compartimentos para posterior integração no DSL.
Essa abordagem para a construção de cartões de pontuação funcionou bem nos anos 90, mas as tecnologias dos pacotes clássicos de mineração de dados estão muito desatualizadas e não permitem o uso de novas técnicas, como, por exemplo, a regularização L2 na regressão, o que pode melhorar significativamente a qualidade dos modelos.
Em um ponto, como um estudo, decidimos reproduzir todas as etapas que os analistas executam ao criar a pontuação, complementá-las com o conhecimento dos cientistas de dados e automatizar o processo inteiro o máximo possível.
Aprimoramento de Python
Como ferramenta de desenvolvimento, escolhemos o Python por sua simplicidade e boas bibliotecas e começamos a executar todas as etapas em ordem.
O primeiro passo é coletar dados e gerar variáveis - esse estágio é uma parte significativa do trabalho dos analistas.
No Python, você pode carregar dados coletados do banco de dados usando o pymysql.
Código para baixar do banco de dadosdef con(): conn = pymysql.connect( host='10.100.10.100', port=3306, user='******* ', password='*****', db='mysql') return conn; df = pd.read_sql(''' SELECT * FROM idf_ru.data_for_scoring ''', con=con())
Em seguida, substituímos os valores raros e ausentes por uma categoria separada para evitar excesso de equipamentos, selecionamos o destino, excluímos as colunas extras e dividimos por treinamento e teste.
Preparação de dados def filling(df): cat_vars = df.select_dtypes(include=[object]).columns num_vars = df.select_dtypes(include=[np.number]).columns df[cat_vars] = df[cat_vars].fillna('_MISSING_') df[num_vars] = df[num_vars].fillna(np.nan) return df def replace_not_frequent(df, cols, perc_min=5, value_to_replace = "_ELSE_"): else_df = pd.DataFrame(columns=['var', 'list']) for i in cols: if i != 'date_requested' and i != 'credit_id': t = df[i].value_counts(normalize=True) q = list(t[t.values < perc_min/100].index) if q: else_df = else_df.append(pd.DataFrame([[i, q]], columns=['var', 'list'])) df.loc[df[i].value_counts(normalize=True)[df[i]].values < perc_min/100, i] =value_to_replace else_df = else_df.set_index('var') return df, else_df cat_vars = df.select_dtypes(include=[object]).columns df = filling(df) df, else_df = replace_not_frequent_2(df, cat_vars) df.drop(['credit_id', 'target_value', 'bor_credit_id', 'bchg_credit_id', 'last_credit_id', 'bcacr_credit_id', 'bor_bonuses_got' ], axis=1, inplace=True) df_train, df_test, y_train, y_test = train_test_split(df, y, test_size=0.33, stratify=df.y, random_state=42)
Agora começa o estágio mais importante na pontuação para regressão - você precisa escrever o bin do WOE para variáveis numéricas e categóricas. No domínio público, não encontramos opções boas e adequadas para nós e decidimos escrever a nós mesmos.
Este artigo de 2017 foi tomado como base da classificação numérica, e também, categoricamente, eles mesmos escreveram do zero. Os resultados foram impressionantes (Gini no teste subiu de 3 a 5 em comparação com os algoritmos de binning de programas externos de mineração de dados).
Depois disso, você pode olhar para os gráficos ou tabelas (que depois escrevemos no Excel) como as variáveis são divididas em grupos e verificar a monotonia:
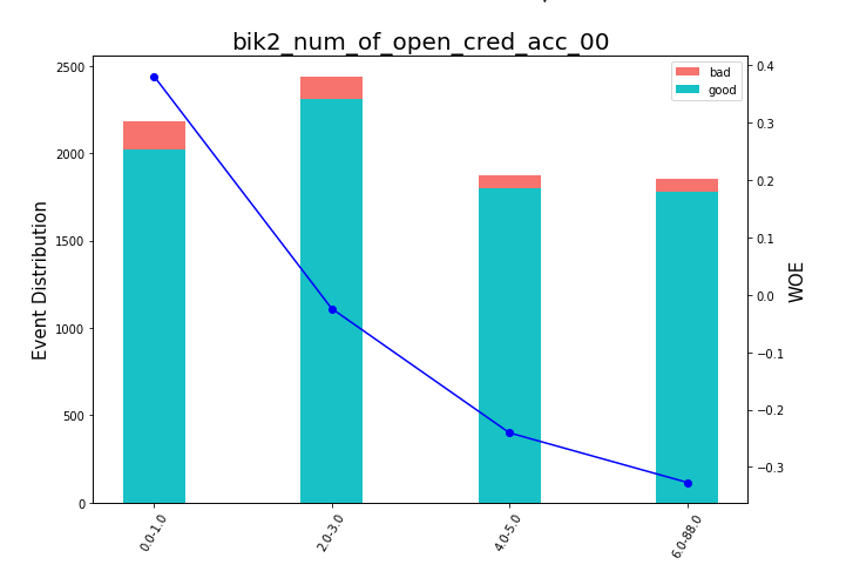
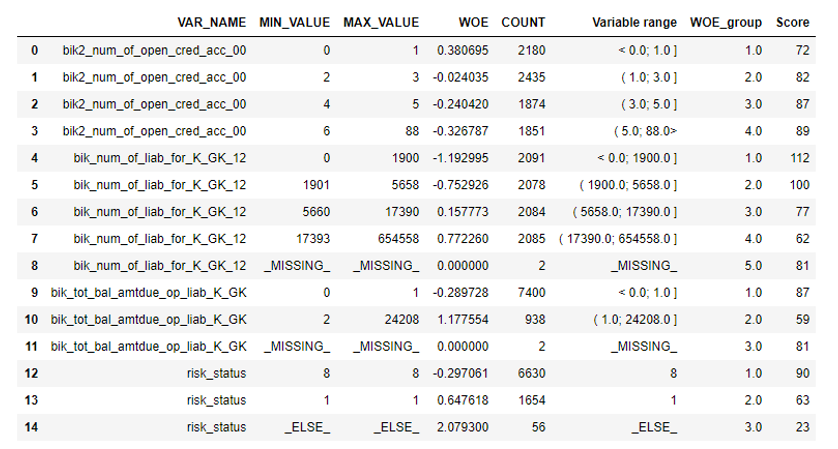
Renderização de gráficos de bean def plot_bin(ev, for_excel=False): ind = np.arange(len(ev.index)) width = 0.35 fig, ax1 = plt.subplots(figsize=(10, 7)) ax2 = ax1.twinx() p1 = ax1.bar(ind, ev['NONEVENT'], width, color=(24/254, 192/254, 196/254)) p2 = ax1.bar(ind, ev['EVENT'], width, bottom=ev['NONEVENT'], color=(246/254, 115/254, 109/254)) ax1.set_ylabel('Event Distribution', fontsize=15) ax2.set_ylabel('WOE', fontsize=15) plt.title(list(ev.VAR_NAME)[0], fontsize=20) ax2.plot(ind, ev['WOE'], marker='o', color='blue')
Uma função para classificação manual foi escrita separadamente, o que é útil, por exemplo, no caso da variável “versão do SO”, na qual todos os telefones Android e iOS foram agrupados manualmente.
Função de escaneamento manual def adjust_binning(df, bins_dict): for i in range(len(bins_dict)): key = list(bins_dict.keys())[i] if type(list(bins_dict.values())[i])==dict: df[key] = df[key].map(list(bins_dict.values())[i]) else:
O próximo passo é a seleção de variáveis por Valor da informação. O valor padrão é cortado em 0,1 (todas as variáveis abaixo não possuem um bom poder preditivo).
Depois disso, foi realizada uma verificação de correlação. Das duas variáveis correlacionadas, você precisa remover a que possui menos IV. A remoção do corte foi realizada 0,75.
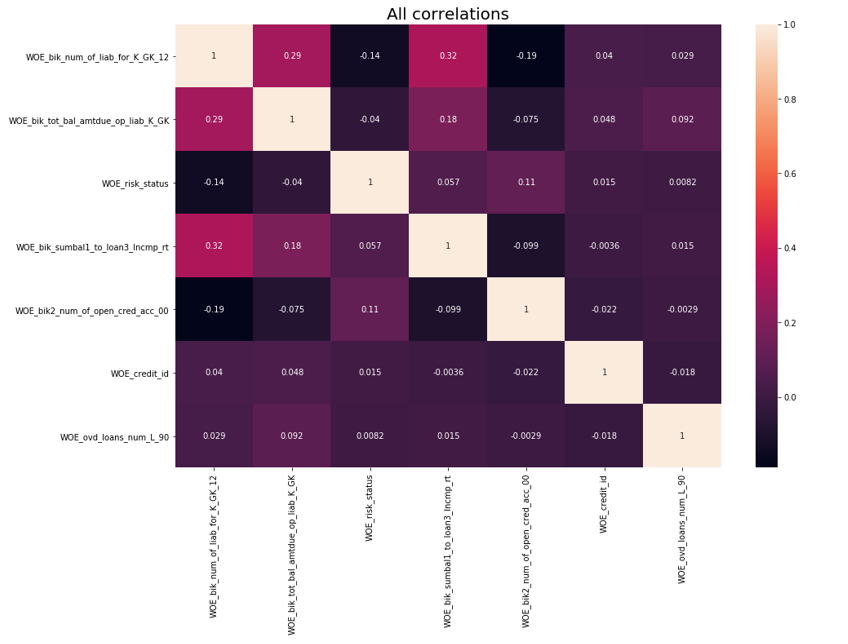
Remoção de Correlação def delete_correlated_features(df, cut_off=0.75, exclude = []):
Além da seleção por IV, adicionamos uma pesquisa recursiva para o número ideal de variáveis pelo método
RFE do sklearn.
Como podemos ver no gráfico, após 13 variáveis, a qualidade não muda, o que significa que as extras podem ser excluídas. Para a regressão, mais de 15 variáveis na pontuação são consideradas más, que na maioria dos casos são corrigidas usando o RFE.
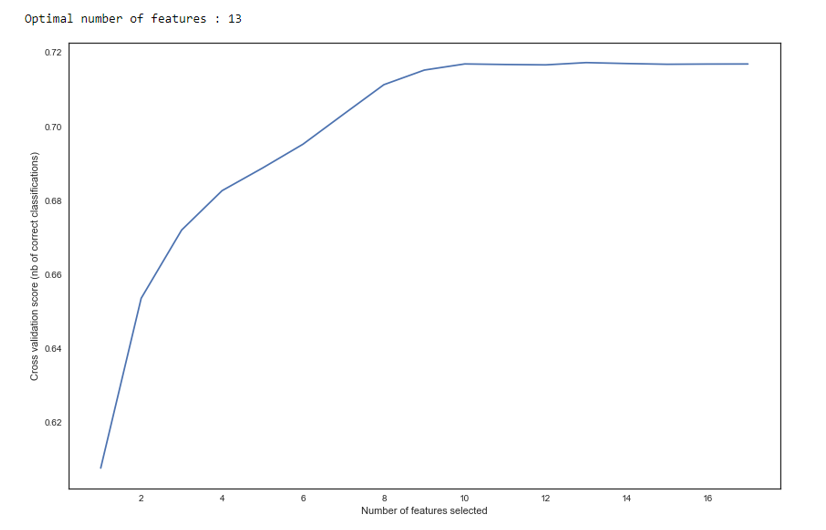
RFE def RFE_feature_selection(clf_lr, X, y): rfecv = RFECV(estimator=clf_lr, step=1, cv=StratifiedKFold(5), verbose=0, scoring='roc_auc') rfecv.fit(X, y) print("Optimal number of features : %d" % rfecv.n_features_)
Em seguida, uma regressão foi construída e suas métricas foram avaliadas na validação cruzada e na amostragem de teste. Geralmente todo mundo olha para o coeficiente de Gini (um bom artigo sobre ele
aqui ).
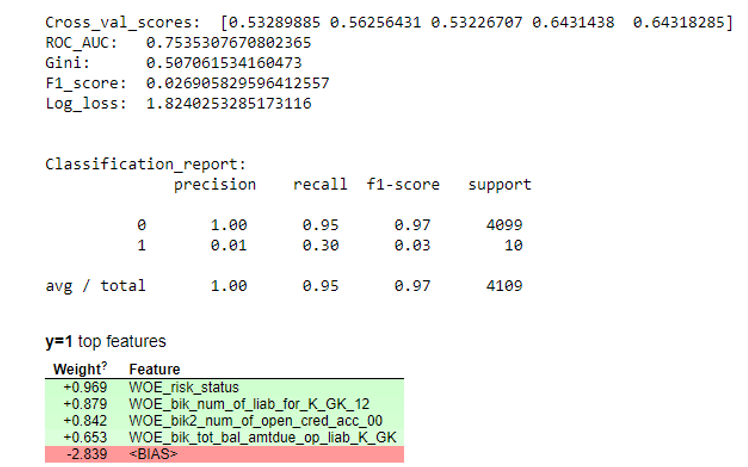
Resultados da simulação def plot_score(clf, X_test, y_test, feat_to_show=30, is_normalize=False, cut_off=0.5):
Quando garantimos que a qualidade do modelo nos convém, é necessário escrever todos os resultados (coeficientes de regressão, grupos de bin, gráficos e variáveis de estabilidade de Gini, etc.) no Excel. Para isso, é conveniente usar o xlsxwriter, que pode funcionar com dados e imagens.
Exemplos de planilhas do Excel:
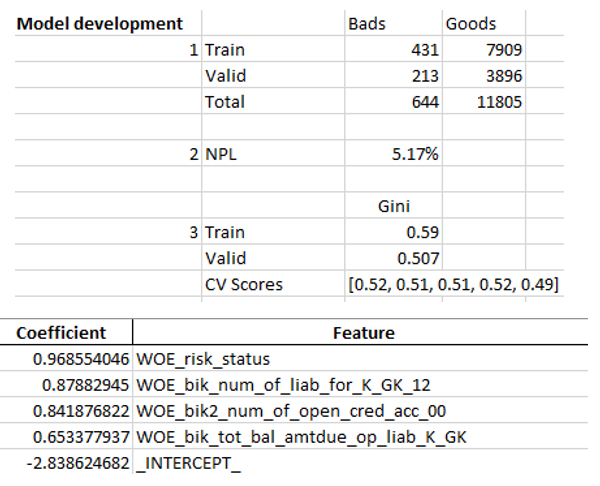
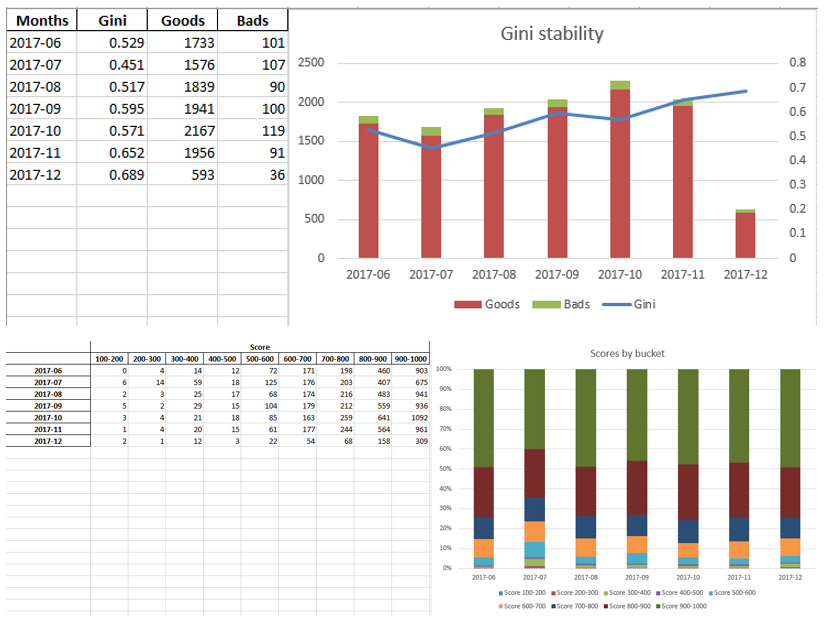
No final, o excel final procura novamente pela gerência, após o qual é atribuído à TI por incorporar o modelo na produção.
Sumário
Como vimos, quase todos os estágios da pontuação podem ser automatizados para que os analistas não precisem de habilidades de programação para criar modelos. No nosso caso, depois de criar essa estrutura, o analista só precisa coletar dados e especificar vários parâmetros (indicar a variável de destino, quais colunas remover, número mínimo de posições, o coeficiente de corte para correlação de variáveis etc.), após o qual você pode executar o script em python, que construirá o modelo e produzirá o excel com os resultados desejados.
Obviamente, às vezes é necessário corrigir o código para as necessidades de um projeto em particular, e você não pode executar um único botão para executar o script durante a modelagem, mas mesmo agora vemos melhor qualidade do que os pacotes de mineração de dados usados no mercado graças a técnicas como bin otimização e monótona, verificação de correlação , RFE, versão regularizada de regressão etc.
Assim, graças ao uso do Python, reduzimos significativamente o tempo de desenvolvimento de cartões de pontuação, bem como reduzimos os custos de mão-de-obra dos analistas.