No filme Missão Impossível 3, foi mostrado o processo de criação das famosas máscaras de espião, graças ao qual alguns personagens se tornam indistinguíveis dos outros. De acordo com o enredo, inicialmente era necessário fotografar a pessoa em que o herói queria se transformar de vários ângulos. Em 2018, um simples modelo de rosto 3D pode até não ser impresso, mas pelo menos criado em formato digital - e com base em apenas uma foto. Um pesquisador da VisionLabs descreveu em detalhes o processo no evento Yandex “
Mundo através dos olhos dos robôs ” da série Data & Science, com detalhes sobre métodos e fórmulas específicas.
Boa tarde Meu nome é Nikolai, trabalho para a VisionLabs, uma empresa de visão computacional. Nosso perfil principal é o reconhecimento facial, mas também temos tecnologias aplicáveis em realidade aumentada e virtual. Em particular, temos uma tecnologia para construir uma face 3D a partir de uma foto, e hoje vou falar sobre isso.

Vamos começar com uma história sobre o que é. No slide, você vê a foto original de Jack Ma e um modelo 3D construído a partir desta foto em duas variações: com e sem textura, apenas geometria. Esta é a tarefa que estamos resolvendo.

Também queremos poder animar esse modelo, mudar a direção do nosso olhar, expressão facial, adicionar expressões faciais etc.
A aplicação está em diferentes áreas. Os mais óbvios são os jogos, incluindo VR. Você também pode fazer provadores virtuais - experimente óculos, barbas e penteados. Você pode imprimir em 3D, porque algumas pessoas estão interessadas em acessórios personalizados para o rosto. E você pode fazer caretas para robôs: imprima e mostre em alguma exibição no robô.

Começarei dizendo como gerar faces 3D em geral e, em seguida, passaremos à tarefa de reconstrução 3D como uma tarefa de geração inversa. Depois disso, focaremos na animação e avançaremos para os desafios que surgem nesta área.

Qual é a tarefa de gerar rostos? Gostaríamos de ter alguma maneira de gerar faces tridimensionais que diferem em forma e expressão. Aqui estão duas linhas com exemplos. A primeira linha mostra faces de diferentes formas, pertencendo como se a pessoas diferentes. E abaixo está a mesma face com uma expressão diferente.

Uma maneira de resolver o problema de geração são os modelos deformáveis. A face mais à esquerda no slide é um tipo de modelo com média para o qual podemos aplicar deformações ajustando os controles deslizantes. Aqui estão três controles deslizantes. Na linha superior, existem faces na direção de aumentar a intensidade do controle deslizante, na linha inferior - na direção de diminuir. Assim, teremos vários parâmetros personalizáveis. Ao instalá-los, você pode dar às pessoas formas diferentes.

Um exemplo de modelo deformável é o famoso Basel Face Model, construído a partir de digitalizações de rosto. Para criar um modelo deformável, você primeiro precisa levar algumas pessoas, levá-las a um laboratório especial e fotografar seus rostos com equipamentos especiais, traduzindo-os para 3D. Então, com base nisso, você pode fazer novas caras.

Como é organizado matematicamente? Podemos imaginar um modelo tridimensional de uma face como um vetor no espaço tridimensional. Aqui n é o número de vértices no modelo, cada vértice corresponde a três coordenadas em 3D e, portanto, obtemos 3n coordenadas.

Se temos um conjunto de varreduras, cada varredura é representada por esse vetor e temos um conjunto de n vetores.
Além disso, podemos construir novas faces como combinações lineares de vetores do nosso banco de dados. Ao mesmo tempo, gostaríamos que os coeficientes fossem significativos. Obviamente, eles não podem ser completamente arbitrários, e logo mostrarei o porquê. Uma das restrições pode ser definida para que todos os coeficientes fiquem no intervalo de 0 a 1. Isso deve ser feito, porque se os coeficientes forem completamente arbitrários, as faces serão implausíveis.

Aqui eu gostaria de dar aos parâmetros algum significado probabilístico. Ou seja, queremos examinar um conjunto de parâmetros e entender se é provável que uma pessoa apareça ou não. Com isso, queremos que distorções baixas correspondam a faces distorcidas.

Aqui está como fazê-lo. Podemos aplicar o método do componente principal a um conjunto de varreduras. Na saída, obtemos a face média S0, obtemos a matriz V, um conjunto de componentes principais e também obtemos variações de dados ao longo dos componentes principais. Depois, podemos dar uma nova olhada na geração de faces, representaremos as faces como uma face média, mais a matriz dos componentes principais, multiplicada pelo vetor de parâmetros.
O valor dos parâmetros é a própria intensidade dos controles deslizantes mencionados em um dos slides anteriores. E também podemos atribuir algum valor probabilístico ao vetor de parâmetros. Em particular, podemos concordar que esse vetor seja gaussiano.

Assim, obtemos um método que permite gerar faces 3D e essa geração é controlada pelos seguintes parâmetros. Como no slide anterior, temos dois conjuntos de parâmetros, dois vetores α id e α exp, eles são os mesmos do slide anterior, mas α id é responsável pelo formato da face e α exp será responsável pela emoção.
Um novo vetor T também aparece - um vetor de textura. Ele tem a mesma dimensão que o vetor de forma e cada vértice nesse vetor tem três valores RGB. Da mesma forma, um vetor de textura é gerado usando o vetor de parâmetro β. Aqui não são formalizados os parâmetros que serão responsáveis por iluminar o rosto e por sua posição, mas também existem.

Aqui estão exemplos de faces que podem ser geradas usando um modelo deformado. Observe que eles diferem em forma, cor da pele e também são desenhados em diferentes condições de iluminação.
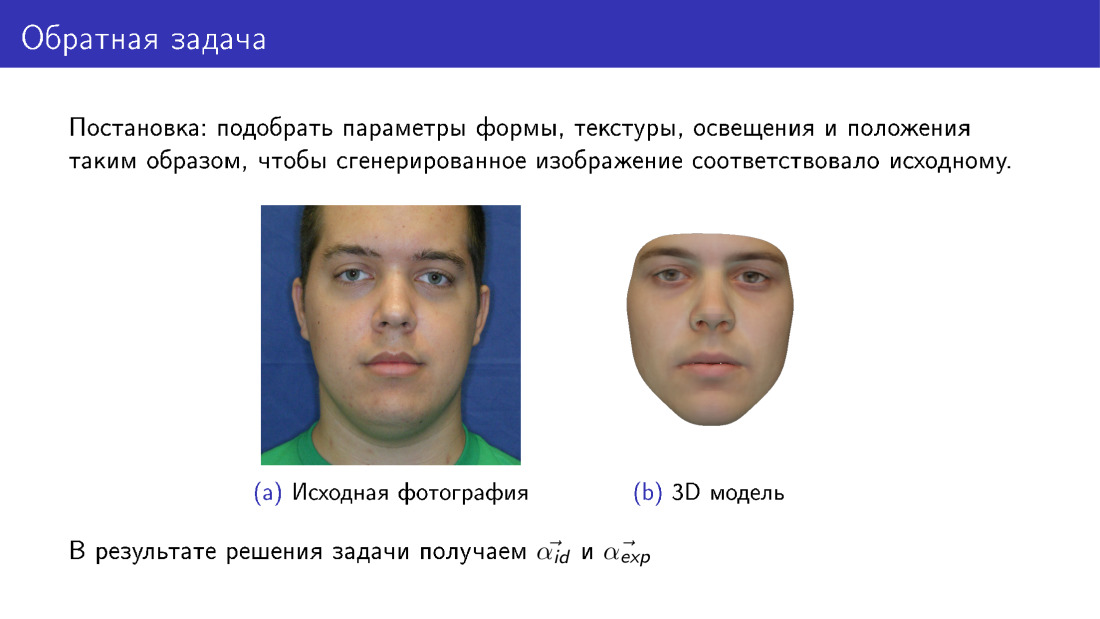
Agora podemos avançar para a reconstrução 3D. Isso é chamado de problema inverso, porque queremos selecionar esses parâmetros para o modelo deformável, de modo que a face que extraímos seja o máximo possível semelhante ao original. Esse slide difere do primeiro, pois aqui, à direita, o rosto é completamente sintético. Se no primeiro slide nossa textura foi tirada de uma fotografia, então aqui a textura foi tirada de um modelo deformável.
Na saída, teremos todos os parâmetros, no slide α id e α exp são apresentados, e também teremos parâmetros de iluminação, textura, etc.

Dissemos que queremos garantir que o modelo gerado pareça uma fotografia. Essa similaridade é determinada usando a função de energia. Aqui apenas consideramos a diferença pixel por pixel das imagens nos pixels em que achamos que o rosto é visível. Por exemplo, se o rosto estiver virado, ocorrerá sobreposição. Por exemplo, parte da maçã do rosto será coberta pelo nariz. E a matriz de visibilidade M deve exibir essa sobreposição.
Em essência, a reconstrução 3D é minimizar essa função de energia. Mas, para resolver esse problema de minimização, seria bom ter inicialização e regularização. A regularização é necessária por uma razão óbvia, pois dissemos que, se não regularizarmos os parâmetros e os tornarmos completamente arbitrários, podemos obter faces distorcidas. A inicialização é necessária porque a tarefa como um todo é complexa, possui mínimos locais e você não deseja lidar com eles.

Como a inicialização pode ser feita? Para isso, você pode usar 68 pontos principais da face. Desde 2013-2014, surgiram muitos algoritmos que permitem a detecção de 68 pontos com uma precisão bastante boa, e agora eles estão se aproximando de uma saturação de sua precisão. Portanto, temos uma maneira de detectar com segurança 68 pontos da face.
Podemos adicionar um novo termo à nossa função energética, o que dirá que queremos que as projeções dos mesmos 68 pontos do modelo coincidam com os pontos principais da face. Marcamos esses pontos no modelo e, de alguma forma, deformamos o modelo, torcemos, projetando os pontos e asseguramos que as posições dos pontos coincidam. Na foto da esquerda, existem pontos de duas cores, violeta e amarelo. Alguns pontos foram detectados pelo algoritmo, enquanto outros foram projetados a partir do modelo. Marcar pontos no modelo à direita, mas para pontos ao longo da borda da face, nenhum ponto é marcado, mas uma linha inteira. Isso é feito porque quando a face é girada, as marcações desses pontos devem mudar e o ponto é selecionado com uma linha.

Aqui está o termo sobre o qual eu falei: é a diferença entre coordenadas de dois vetores que descreve os pontos-chave da face e os pontos-chave projetados a partir do modelo.

Voltemos à regularização e consideremos todo o problema da perspectiva da conclusão bayesiana. A probabilidade de o vetor α ser igual a algo dado em uma imagem conhecida é proporcional ao produto da probabilidade de observar a imagem para um dado α, multiplicado pela probabilidade α. Se tomarmos o logaritmo negativo dessa expressão, que teremos que minimizar, veremos que o termo responsável pela regularização terá uma forma concreta aqui. Em particular, este é o segundo termo. Lembrando que anteriormente assumimos que o vetor α é gaussiano, vemos que o termo responsável pela regularização é a soma dos quadrados dos parâmetros reduzidos a variações ao longo dos componentes principais.

Assim, podemos escrever a função de energia completa, que contém três termos. O primeiro termo é responsável pela textura, pela diferença de pixels entre a imagem gerada e a imagem de destino. O segundo termo é responsável por pontos-chave e o terceiro é responsável pela regularização.
Os coeficientes dos termos no processo de minimização não são otimizados, são simplesmente definidos.
Aqui, a função de energia é representada como uma função de todos os parâmetros. parâmetros de forma α id - face, parâmetros α exp - expressão, parâmetros β - textura, p - outros parâmetros sobre os quais falamos, mas não formalizamos, são parâmetros de posição e iluminação.
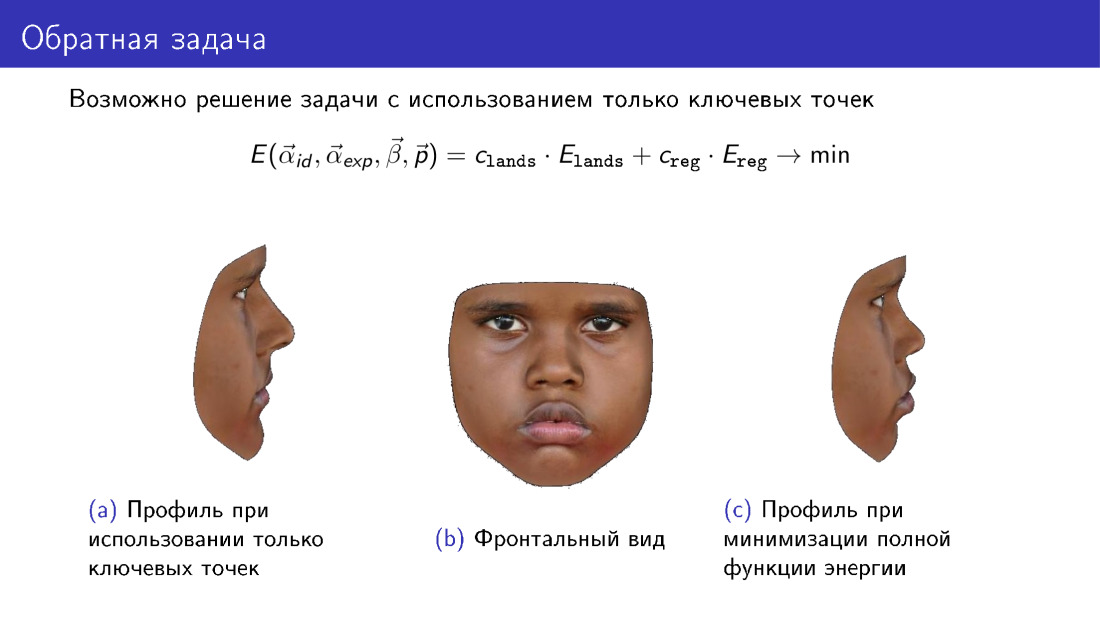
Vamos nos debruçar sobre esta observação. Esta função de energia pode ser simplificada. A partir dele, você pode descartar o termo responsável pela textura e usar apenas as informações transmitidas por 68 pontos. E isso permitirá que você crie algum tipo de modelo 3D. No entanto, preste atenção ao perfil do modelo. À esquerda, há um modelo construído apenas em pontos-chave. À direita está um modelo usando textura ao construir. Observe que o perfil à direita é mais consistente com a fotografia central, que representa a vista frontal do rosto.

A animação com o algoritmo existente para a construção de um modelo 3D da face funciona de maneira bastante simples. Lembre-se de que, ao criar um modelo 3D, obtemos dois vetores de parâmetros, um responsável pela forma e o outro pela expressão. Esses vetores de parâmetros para o usuário e o avatar sempre terão seus próprios. O usuário tem um vetor de parâmetros de formulário, o avatar tem um vetor diferente. No entanto, podemos tornar os vetores responsáveis pela expressão os mesmos. Vamos pegar os parâmetros responsáveis pela expressão facial do usuário e simplesmente substituí-los no modelo de avatar. Assim, transferiremos a expressão facial do usuário para o avatar.
Vamos falar sobre dois desafios nessa área: a velocidade do trabalho e o modelo deformável limitado.

A velocidade é realmente um problema. Minimizar a função total de energia é uma tarefa muito computacionalmente intensiva. Em particular, pode levar de 20 a 40, em média 30 segundos. Isso é longo o suficiente. Se construirmos um modelo tridimensional apenas em pontos-chave, ele será muito mais rápido, mas a qualidade sofrerá com isso.

Como lidar com este problema? Você pode usar mais recursos, algumas pessoas resolvem esse problema na GPU. Somente pontos-chave podem ser usados, mas a qualidade sofrerá. E você pode usar métodos de aprendizado de máquina.

Vamos ver em ordem. Aqui está o trabalho de 2016, no qual a expressão facial do usuário é transferida para um vídeo específico, você pode controlar o vídeo usando seu rosto. Aqui, a construção do modelo 3D é realizada em tempo real usando a GPU.

Aqui estão os métodos que usam o aprendizado de máquina. A idéia é que podemos primeiro pegar uma grande base de faces, para cada face usando um algoritmo longo mas preciso para criar modelos 3D, apresentar cada modelo como um conjunto de parâmetros e depois treinar a grade para prever esses parâmetros. Em particular, neste trabalho de 2016, é utilizado o ResNet, que leva uma imagem para a entrada e fornece os parâmetros do modelo para a saída.

O modelo tridimensional pode ser representado de outra maneira. Neste trabalho de 2017, o modelo 3D é apresentado não como um conjunto de parâmetros, mas como um conjunto de voxels. A rede prevê voxels, transformando a imagem em uma representação tridimensional. Vale ressaltar que são possíveis opções de treinamento em rede para as quais os modelos 3D não são necessários.

Isso funciona da seguinte maneira. Aqui, a parte mais importante é a camada, que pode pegar os parâmetros do modelo deformável como entrada e renderizar a imagem. Tem uma propriedade tão maravilhosa que, através dela, você pode fazer a propagação de volta do erro. A rede aceita uma imagem como entrada, prediz os parâmetros, alimenta esses parâmetros para uma camada que renderiza a imagem, compara essa imagem com a entrada, recebe um erro, propaga o erro de volta e continua aprendendo. Assim, a rede aprende a prever os parâmetros do modelo tridimensional, tendo apenas figuras como dados de treinamento. E isso é muito interessante.

Conversamos muito sobre precisão - em particular, que ela sofre se descartamos alguns termos da função da energia. Vamos formalizar o que isso significa, como você pode avaliar a precisão da reconstrução de face 3D. Para fazer isso, precisamos de uma base de verificações da verdade verdade obtidas usando equipamento especial, usando métodos com relação aos quais existem algumas garantias de precisão. Se essa base existe, podemos comparar nossos modelos reconstruídos com a verdade básica. Isso é feito simplesmente: calculamos a distância média dos vértices do nosso modelo, que construímos, aos vértices na verdade do solo e normalizamos o tamanho da varredura. Isso deve ser feito porque as faces são diferentes, algumas são maiores, algumas são menores e o erro na face menor seria menor, simplesmente porque a face em si é menor. Portanto, a normalização é necessária.

Eu gostaria de falar sobre o nosso trabalho, será em oficinas, há ECCV. Fazemos coisas semelhantes, ensinamos o MobileNet a prever os parâmetros de um modelo deformável. Como dados de treinamento, usamos modelos 3D criados para fotografias do conjunto de dados de 300W. Avalie a precisão com base nas digitalizações BU4DFE.
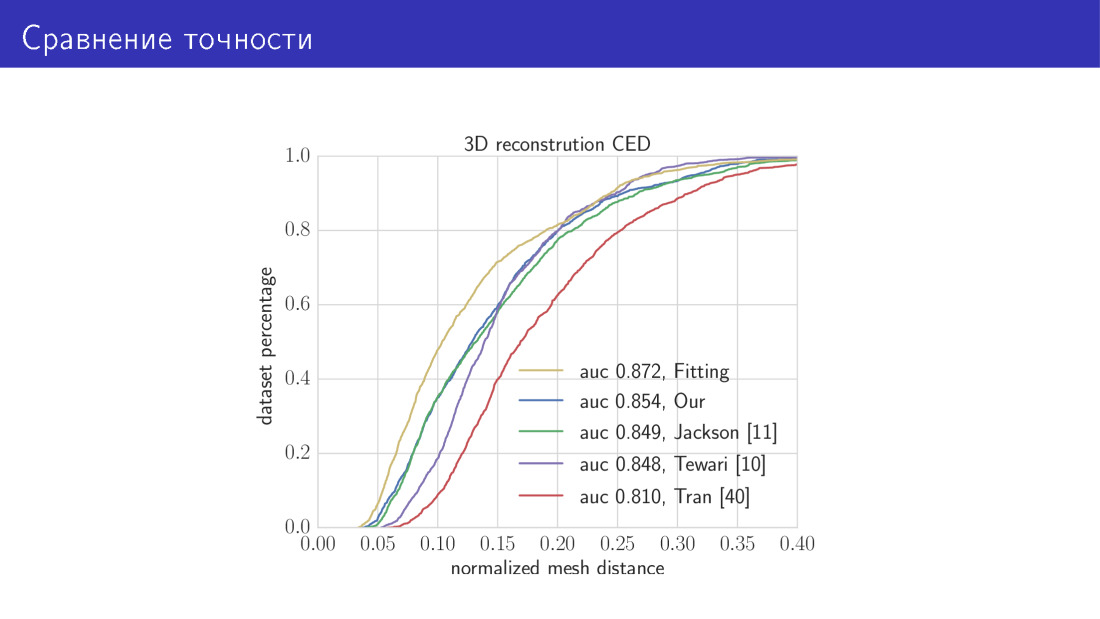
Aqui está o resultado. Comparamos nossos dois algoritmos com o estado da arte. A curva amarela neste gráfico é um algoritmo que leva 30 segundos e consiste em minimizar a função de energia total. Aqui, no eixo X, está o erro que acabamos de falar, a distância média entre os vértices. O eixo Y é a fração de imagens em que esse erro é menor que o do eixo X. Nesse gráfico, quanto maior a curva, melhor. A próxima curva é a nossa rede baseada em MobileNet. A seguir, os três trabalhos sobre os quais falamos. Rede preditiva de parâmetros e rede preditiva de voxel.
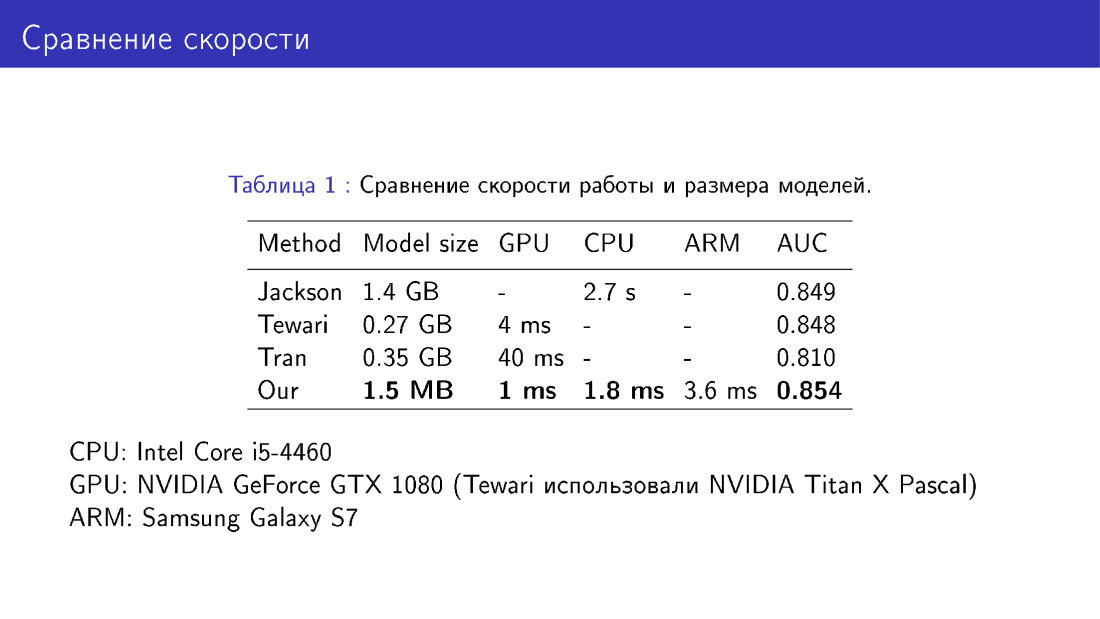
Também comparamos nossa rede com colegas em termos de tamanho e velocidade do modelo. Esta é uma vitória, porque usamos o MobileNet, o que é bastante fácil.
O segundo desafio é a limitação do modelo deformável.

Preste atenção na face esquerda, observe as asas do nariz. Há sombras nas asas do nariz. As bordas das sombras não coincidem com as bordas do nariz na foto, portanto, um defeito é obtido. A razão para isso pode ser que o modelo deformável, em princípio, não é capaz de construir o nariz da forma requerida, porque esse modelo deformável foi obtido a partir de digitalizações de apenas 200 faces. Gostaríamos que o nariz estivesse correto, como na foto certa. Portanto, precisamos de alguma forma ir além da estrutura do modelo deformável.

Isso pode ser feito usando deformação não paramétrica da malha. Aqui estão três tarefas que gostaríamos de resolver: modificar a parte local da face, por exemplo, o nariz, incorporá-la no modelo original da face e até mesmo para que todo o resto permaneça inalterado.

Isso pode ser feito da seguinte maneira. Voltemos à designação da malha como um vetor no espaço tridimensional e observemos o operador de média. Este é um operador que em S com um cabeçalho substitui cada vértice pela média de seus vizinhos. Os vizinhos do pico são aqueles que estão conectados a ele por uma borda.
Definiremos uma certa função energética que descreve a posição do vértice em relação aos seus vizinhos. Queremos que a posição do pico em relação aos seus vizinhos permaneça inalterada, ou pelo menos não mude muito. Mas, ao mesmo tempo, modificaremos S. de alguma forma. Essa função energética é chamada interna, porque também haverá algum termo externo, que dirá que, por exemplo, o nariz deve assumir uma determinada forma.
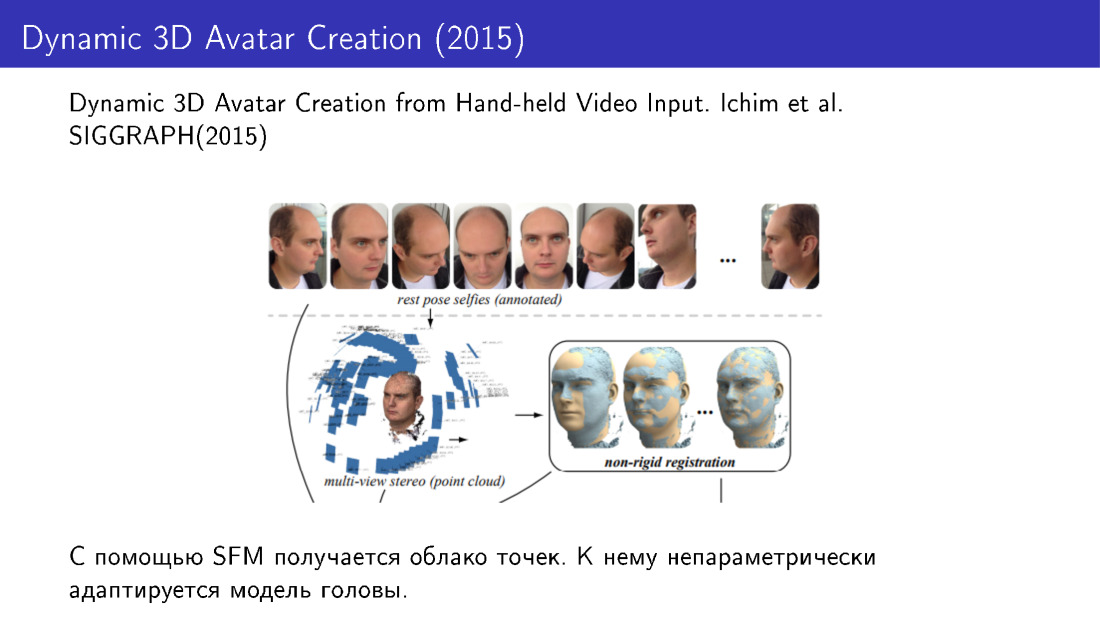
Tais técnicas foram utilizadas, por exemplo, no trabalho de 2015. Eles fizeram a reconstrução do rosto em 3D a partir de várias fotografias. Tiramos várias fotos do telefone, recebemos uma nuvem de pontos e adaptamos o modelo de face a essa nuvem usando modificações não paramétricas.
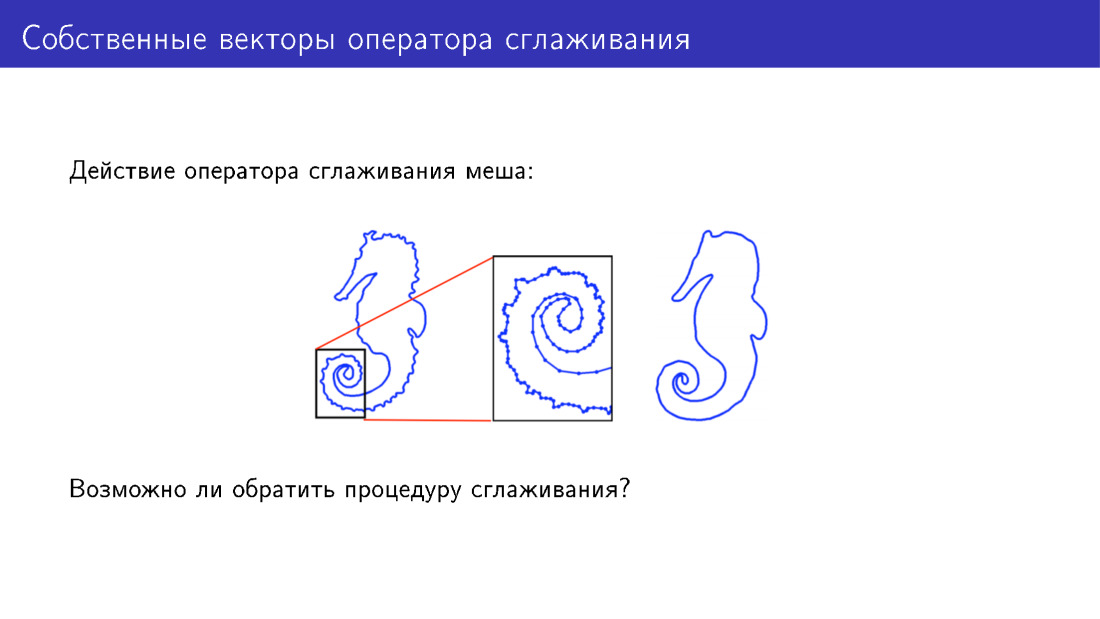
Você pode ir além do modelo deformável de outra maneira. Vamos nos concentrar na ação do operador de suavização. Aqui, por simplicidade, é apresentada uma malha bidimensional à qual esse operador foi aplicado. Existem muitos detalhes no modelo à esquerda; no modelo à direita, esses detalhes foram suavizados. Mas podemos fazer algo para adicionar detalhes em vez de removê-los?

. .
? -: - . . , 2016 . , .