Lutei com a tentação de nomear o artigo como "A aterradora ineficiência dos algoritmos STL" - você sabe, apenas por uma questão de treinamento na arte de criar manchetes chamativas. Mas, no entanto, ele decidiu permanecer dentro dos limites da decência - é melhor receber comentários dos leitores sobre o conteúdo do artigo do que indignação por seu grande nome.
Neste ponto, assumirei que você conhece um pouco de C ++ e STL e também cuida dos algoritmos usados em seu código, de sua complexidade e relevância para as tarefas.
Algoritmos
Uma das dicas bem conhecidas que você pode ouvir da moderna comunidade de desenvolvedores de C ++ não é criar bicicletas, mas usar algoritmos da biblioteca padrão. Este é um bom conselho. Esses algoritmos são seguros, rápidos, testados ao longo dos anos. Também dou conselhos sobre como aplicá-los.
Toda vez que você quiser escrever outro, lembre-se primeiro de que existe algo no STL (ou impulso) que já resolve esse problema em uma linha. Se houver, geralmente é melhor usar isso. Entretanto, nesse caso, também devemos entender que tipo de algoritmo está por trás da chamada da função padrão, quais são suas características e limitações.
Normalmente, se o nosso problema corresponder exatamente à descrição do algoritmo da STL, seria uma boa ideia utilizá-lo e aplicá-lo na "testa". O único problema é que os dados nem sempre são armazenados na forma em que o algoritmo implementado na biblioteca padrão deseja recebê-los. Em seguida, podemos ter a ideia de primeiro converter os dados e ainda aplicar o mesmo algoritmo. Bem, você sabe, como naquela piada de matemática “Apague o fogo da chaleira. A tarefa é reduzida à anterior.
Interseção de conjuntos
Imagine que estamos tentando escrever uma ferramenta para programadores C ++ que encontre todas as lambdas no código com a captura de todas as variáveis padrão ([=] e [&]) e exiba dicas para convertê-las em lambdas com uma lista específica de variáveis capturadas. Algo assim:
std::partition(begin(elements), end(elements), [=] (auto element) {
No processo de análise do arquivo com o código, teremos que armazenar a coleção de variáveis em algum lugar no escopo atual e circundante, e se um lambda for detectado com a captura de todas as variáveis, compare essas duas coleções e dê conselhos sobre sua conversão.
Um conjunto com variáveis no escopo pai e outro com variáveis dentro do lambda. Para formar conselhos, o desenvolvedor precisa apenas encontrar seu cruzamento. E é esse o caso quando a descrição do algoritmo da STL é perfeita para a tarefa:
std :: set_intersection pega dois conjuntos e retorna sua interseção. O algoritmo é bonito em sua simplicidade. Ele pega duas coleções classificadas e as percorre em paralelo:
- Se o item atual na primeira coleção for idêntico ao item atual na segunda - adicione-o ao resultado e vá para os próximos itens nas duas coleções
- Se o item atual na primeira coleção for menor que o item atual na segunda coleção, vá para o próximo item na primeira coleção
- Se o item atual na primeira coleção for maior que o item atual na segunda coleção, vá para o próximo item na segunda coleção
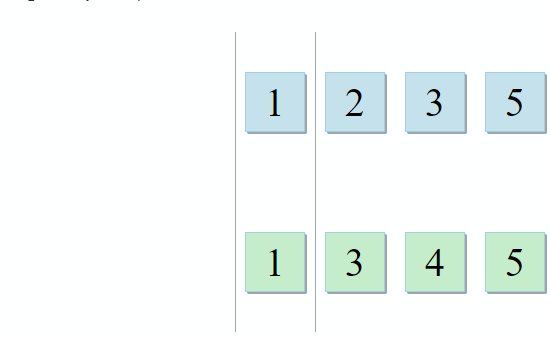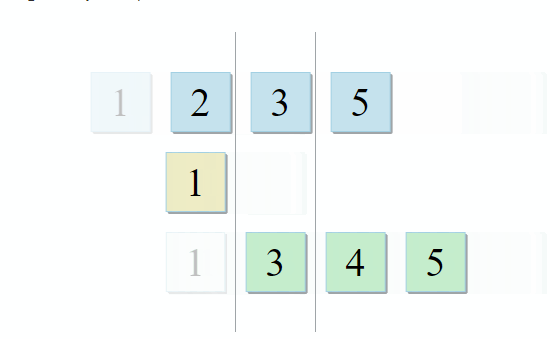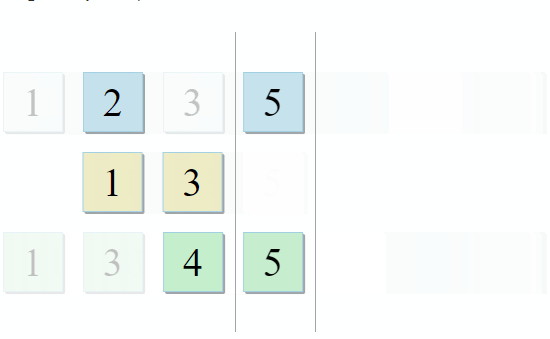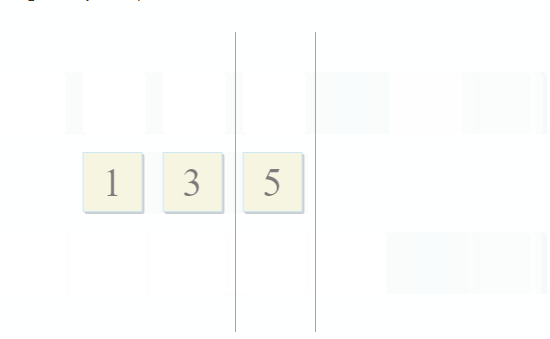
Com cada etapa do algoritmo, movemos a primeira, a segunda ou as duas coleções, o que significa que a complexidade desse algoritmo será linear - O (m + n), onde n e m são os tamanhos das coleções.
Simples e eficaz. Mas isso é apenas até agora as coleções de entrada são classificadas.
Classificação
O problema é que, em geral, as coleções não são classificadas. Em nosso caso específico, é conveniente armazenar variáveis em alguma estrutura de dados do tipo pilha, adicionando variáveis ao próximo nível de pilha ao inserir um escopo aninhado e removendo-as da pilha ao sair desse escopo.
Isso significa que as variáveis não serão classificadas por nome e não podemos usar diretamente std :: set_intersection em suas coleções. Como std :: set_intersection requer coleções exatamente classificadas na entrada, a idéia pode surgir (e eu frequentemente vi essa abordagem em projetos reais) para classificar coleções antes de chamar a função de biblioteca.
A classificação nesse caso eliminará toda a idéia de usar uma pilha para armazenar variáveis de acordo com seu escopo, mas ainda é possível:
template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_1(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { std::sort(first1, last1); std::sort(first2, last2); return std::set_intersection(first1, last1, first2, last2, dest); }
Qual é a complexidade do algoritmo resultante? Algo como O (n log n + m log m + n + m) é uma complexidade quase linear.
Menos classificação
Não podemos usar a classificação? Nós podemos, por que não? Apenas procuraremos cada elemento da primeira coleção na segunda pesquisa linear. Temos a complexidade O (n * m). E também vi essa abordagem em projetos reais com bastante frequência.
Em vez das opções "classificar tudo" e "não classificar nada", podemos tentar encontrar o Zen e seguir o terceiro caminho - classifique apenas uma das coleções. Se uma das coleções é classificada, mas a segunda não, podemos iterar os elementos da coleção não classificada, um de cada vez, e procurá-los na pesquisa binária classificada.
A complexidade desse algoritmo será O (n log n) para classificar a primeira coleção e O (m log n) para pesquisar e verificar. No total, obtemos a complexidade O ((n + m) log n).
Se decidirmos classificar outra das coleções, obteremos a complexidade O ((n + m) log m). Como você entende, seria lógico classificar uma coleção menor aqui para obter a complexidade final O ((m + n) log (min (m, n))
A implementação terá a seguinte aparência:
template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_2(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { const auto size1 = std::distance(first1, last1); const auto size2 = std::distance(first2, last2); if (size1 > size2) { unordered_intersection_2(first2, last2, first1, last1, dest); return; } std::sort(first1, last1); return std::copy_if(first2, last2, dest, [&] (auto&& value) { return std::binary_search(first1, last1, FWD(value)); }); }
Em nosso exemplo com funções lambda e captura de variáveis, a coleção que classificaremos geralmente será a coleção de variáveis usadas no código da função lambda, pois é provável que haja menos variáveis do que as variáveis no escopo lambda circundante.
Hashing
E a última opção discutida neste artigo será usar hash para uma coleção menor em vez de classificá-la. Isso nos dará a oportunidade de procurar O (1) nele, embora a construção do hash, claro, leve algum tempo (de O (n) a O (n * n), o que pode se tornar um problema):
template <typename InputIt1, typename InputIt2, typename OutputIt> void unordered_intersection_3(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { const auto size1 = std::distance(first1, last1); const auto size2 = std::distance(first2, last2); if (size1 > size2) { unordered_intersection_3(first2, last2, first1, last1, dest); return; } std::unordered_set<int> test_set(first1, last1); return std::copy_if(first2, last2, dest, [&] (auto&& value) { return test_set.count(FWD(value)); }); }
A abordagem de hash será vencedora absoluta quando nossa tarefa for comparar consistentemente um pequeno conjunto A com um conjunto de outros conjuntos (grandes) B₁, B₂, B .... Nesse caso, precisamos construir um hash para A apenas uma vez e podemos usar sua pesquisa instantânea para compará-lo com os elementos de todos os conjuntos B em consideração.
Teste de desempenho
É sempre útil confirmar a teoria com a prática (especialmente em casos como o último, quando não está claro se os custos iniciais do hash serão recompensados com um ganho no desempenho da pesquisa).
Nos meus testes, a primeira opção (com a classificação das duas coleções) sempre mostrou os piores resultados. Classificar apenas uma coleção menor funcionou um pouco melhor em coleções do mesmo tamanho, mas não muito. Mas o segundo e o terceiro algoritmos mostraram um aumento muito significativo na produtividade (cerca de 6 vezes) nos casos em que uma das coleções era 1000 vezes maior que a outra.