Este artigo é uma continuação lógica da introdução de shaders de programação para designers de layout . Nele, criamos um modelo para criar vários efeitos bidimensionais com fotos usando shaders e analisamos alguns exemplos. Neste artigo, adicionaremos mais algumas texturas, aplicaremos a divisão de Voronoi na prática para criar mosaicos a partir deles, falar sobre a criação de várias máscaras em shaders, sobre pixelização e também abordar alguns problemas da antiga sintaxe GLSL que ainda existe em nossos navegadores.
Assim como da última vez, haverá um mínimo de teoria e um máximo de prática e raciocínio em uma linguagem cotidiana mundana. Os iniciantes encontrarão aqui uma sequência de ações com dicas e notas úteis, e fornecedores experientes de front-end podem encontrar algumas idéias para se inspirar.
Uma pesquisa em um artigo anterior mostrou que o tópico de efeitos WebGL para sites pode ser de interesse não apenas para os tipógrafos, mas também para nossos colegas de outras especializações. Para não confundi-los com os recursos mais recentes de ES, nos restringimos deliberadamente a construções de sintaxe mais tradicionais que todos entendem. E, novamente, chamo a atenção dos leitores para o fato de que os editores internos do CodePen afetam o desempenho do que é feito neles.
Mas vamos começar ...
Modelo para trabalhar com shaders
Para quem não leu o artigo anterior, criamos este modelo para trabalhar com shaders:
É criado um plano (no nosso caso, um quadrado) no qual a textura da imagem é "desenhada". Sem dependências desnecessárias e um shader de vértice muito simples. Em seguida, desenvolvemos esse modelo, mas agora começaremos a partir do momento em que ainda não há lógica no sombreador de fragmentos.
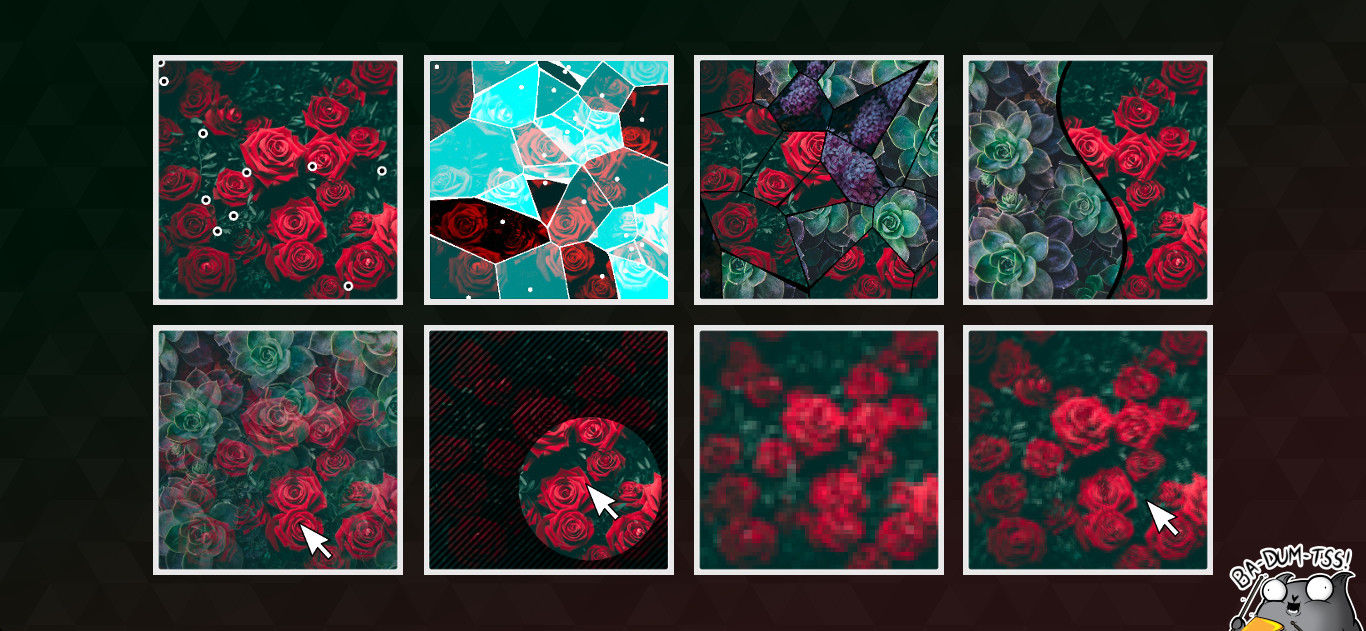
Mosaico
Mosaico é um plano dividido em pequenas áreas, onde cada uma das áreas é preenchida com uma determinada cor ou, como no nosso caso, textura. Como podemos até quebrar nosso avião em pedaços? Obviamente, você pode dividi-lo em retângulos. Mas isso já é tão fácil com a ajuda do SVG, arrastar o WebGL para esta tarefa e colocar tudo do nada sem absolutamente nenhum propósito.
Para que o mosaico seja interessante, ele deve ter fragmentos diferentes, tanto na forma quanto no tamanho. Existe uma abordagem muito simples, mas ao mesmo tempo divertida, para a construção dessa partição. É conhecido como mosaico de Voronoi ou partição de Dirichlet, e na Wikipedia eles escrevem que Descartes usou algo semelhante no distante século XVII. A ideia é mais ou menos assim:
- Pegue um conjunto de pontos no avião.
- Para cada ponto no plano, encontre o ponto mais próximo deste conjunto.
- Só isso. O plano é dividido em áreas poligonais, cada uma das quais é determinada por um dos pontos do conjunto.
Provavelmente é melhor mostrar esse processo com um exemplo prático. Existem algoritmos diferentes para gerar essa partição, mas agiremos na testa, porque calcular algo para cada ponto no plano é apenas a tarefa do shader. Primeiro, precisamos fazer um conjunto de pontos aleatórios. Para não carregar o código dos exemplos, criaremos uma variável global para eles.
function createPoints() { for (let i = 0; i < NUMBER_OF_POINTS; i++) { POINTS.push([Math.random(), Math.random()]); } }
Agora precisamos passá-los para os shaders. Como os dados são globais, usaremos o modificador uniform . Mas há um ponto sutil: não podemos simplesmente passar uma matriz. Parece que o século XXI está no quintal, mas, no entanto, nada resultará disso. Como resultado, você deve transferir uma matriz de pontos, um de cada vez.
for (let i = 0; i < NUMBER_OF_POINTS; i++) { GL.uniform2fv(GL.getUniformLocation(PROGRAM, 'u_points[' + i + ']'), POINTS[i]); }
Hoje, frequentemente encontramos problemas semelhantes de inconsistência entre o que é esperado e o que está em navegadores reais. Geralmente, os tutoriais do WebGL usam THREE.js e essa biblioteca oculta parte da sujeira, como o jQuery fazia em suas tarefas, mas se você a remover, isso realmente prejudicará seu cérebro.
No shader de fragmento, temos uma variável de matriz para pontos. Só podemos criar matrizes de comprimento fixo. Vamos começar com 10 pontos:
#define NUMBER_OF_POINTS 10 uniform vec2 u_points[NUMBER_OF_POINTS];
Certifique-se de que tudo isso esteja funcionando, desenhando círculos nos locais dos pontos. Esse desenho de várias primitivas geométricas é frequentemente usado durante a depuração - elas são claramente visíveis e você pode entender imediatamente o que está localizado e para onde está se movendo.
Use o "desenho" de círculos, linhas e outros pontos de referência para os objetos invisíveis nos quais as animações são construídas. Isso fornecerá pistas óbvias sobre como eles funcionam, especialmente se os algoritmos forem complexos para entender rapidamente sem preparação prévia. Então, tudo isso pode ser comentado e deixado para os colegas - eles agradecem.
for (int i = 0; i < NUMBER_OF_POINTS; i++) { if (distance(texture_coord, u_points[i]) < 0.02) { gl_FragColor = WHITE; break; } }
Bom Vamos também adicionar algum movimento aos pontos. Deixe que eles se movam em círculo para começar, depois retornaremos a esse problema. Os coeficientes também são colocados no olho, apenas para desacelerar levemente o movimento e reduzir a amplitude das oscilações.
function movePoints(timeStamp) { if (timeStamp) { for (let i = 0; i < NUMBER_OF_POINTS; i++) { POINTS[i][0] += Math.sin(i * timeStamp / 5000.0) / 500.0; POINTS[i][1] += Math.cos(i * timeStamp / 5000.0) / 500.0; } } }
Volte para o shader. Para experimentos futuros, encontraremos números úteis de áreas nas quais tudo será dividido. Portanto, encontramos o ponto mais próximo ao pixel atual do conjunto e salvamos o número desse ponto - é o número da área.
float min_distance = 1.0; int area_index = 0; for (int i = 0; i < NUMBER_OF_POINTS; i++) { float current_distance = distance(texture_coord, u_points[i]); if (current_distance < min_distance) { min_distance = current_distance; area_index = i; } }
Para testar o desempenho, pintamos tudo novamente em cores brilhantes:
gl_FragColor = texture2D(u_texture, texture_coord); gl_FragColor.g = abs(sin(float(area_index))); gl_FragColor.b = abs(sin(float(area_index)));
A combinação de módulo (abs) e funções limitadas (em particular sin e cos) são frequentemente usadas quando se trabalha com efeitos semelhantes. Por um lado, isso adiciona um pouco de aleatoriedade e, por outro lado, fornece imediatamente um resultado normalizado de 0 a 1, o que é muito conveniente - temos muitos valores que estão exatamente dentro desses limites.
Também encontraremos pontos mais ou menos equidistantes de vários pontos do conjunto e os coloriremos. Essa ação não carrega uma carga útil especial, mas observar o resultado ainda é interessante.
int number_of_near_points = 0; for (int i = 0; i < NUMBER_OF_POINTS; i++) { if (distance(texture_coord, u_points[i]) < min_distance + EPSILON) { number_of_near_points++; } } if (number_of_near_points > 1) { gl_FragColor.rgb = vec3(1.0); }
Você deve obter algo como isto:
Ainda é um rascunho, ainda estaremos finalizando. Mas agora o conceito geral de tal separação do avião está claro.
Mosaico de fotos
É claro que, em sua forma pura, não há muitos benefícios com essa partição. Para ampliar seus horizontes e apenas por diversão, você pode brincar com ele, mas em um site real vale a pena adicionar mais algumas fotos e fazer um mosaico delas. Vamos refazer um pouco a função de criar texturas, para que haja mais de uma.
function createTextures() { for (let i = 0; i < URLS.textures.length; i++) { createTexture(i); } } function createTexture(index) { const image = new Image(); image.crossOrigin = 'anonymous'; image.onload = () => { const texture = GL.createTexture(); GL.activeTexture(GL['TEXTURE' + index]); GL.bindTexture(GL.TEXTURE_2D, texture); GL.pixelStorei(GL.UNPACK_FLIP_Y_WEBGL, true); GL.texImage2D(GL.TEXTURE_2D, 0, GL.RGB, GL.RGB, GL.UNSIGNED_BYTE, image); GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_WRAP_S, GL.CLAMP_TO_EDGE); GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_WRAP_T, GL.CLAMP_TO_EDGE); GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_MIN_FILTER, GL.LINEAR); GL.uniform1i(GL.getUniformLocation(PROGRAM, 'u_textures[' + index + ']'), index); }; image.src = URLS.textures[index]; }
Nada de anormal aconteceu, apenas substituímos os zeros pelo parâmetro index e reutilizamos o código existente para carregar as três texturas. No shader, agora temos uma variedade de texturas:
#define NUMBER_OF_TEXTURES 3 uniform sampler2D u_textures[NUMBER_OF_TEXTURES];
Agora podemos usar o número da área salvo anteriormente para selecionar uma das três texturas. Mas ...
Mas antes disso eu gostaria de fazer uma pequena digressão. Sobre dor. Sobre a sintaxe. Javascript moderno (condicionalmente ES6 +) é uma linguagem agradável. Ele permite que você expresse seus pensamentos à medida que surgem, não limita a estrutura a nenhum paradigma de programação específico, completa alguns pontos para nós e permite que você se concentre mais na idéia do que na sua implementação. Para o criador - é isso. Algumas pessoas acreditam que isso dá muita liberdade e mudam para o TypeScript, por exemplo. Pure C é uma linguagem mais rigorosa. Também permite muito, você pode atrair qualquer coisa, mas após o JS é percebido como um pouco estranho, antiquado ou algo assim. No entanto, ele ainda é bom. GLSL como existe nos navegadores é apenas algo. Além de ser uma ordem de magnitude mais rigorosa que C, ainda falta muitos operadores e construções de sintaxe conhecidos. Este é provavelmente o maior problema ao escrever shaders mais ou menos complexos para o WebGL. Por trás do horror em que o código se transforma, pode ser muito difícil dar uma olhada no algoritmo original. Alguns programadores pensam que até aprender C, o caminho para os shaders está fechado para eles. Portanto: o conhecimento de C não ajudará particularmente aqui. Aqui está algum tipo de mundo próprio. O mundo da loucura, dinossauros e muletas.
Como posso escolher uma das três texturas com um número - o número da área. O restante vem à mente de dividir o número pelo número de texturas. Ótima ideia. Somente o operador % , que as próprias mãos já escrevem, não está aqui. A impressão de entender esse fato é bem descrita pela figura:

Claro, você diz: "Sim, não há problema, existe uma função mod - vamos aceitá-la!". Mas acontece que ela não aceita dois inteiros, apenas fracionários. Ok, bem, faça-os float . Também temos um float , mas precisamos de um int . Você precisa converter tudo de volta, caso contrário, há uma chance não falsa de obter um erro de compilação.
int texture_index = int(mod(float(area_index), float(NUMBER_OF_TEXTURES)))
E aqui está uma pergunta retórica: talvez seja mais fácil realizar sua função do restante da divisão inteira do que tentar montá-la a partir de métodos padrão? E essa ainda é uma função simples, e acontece que sequências muito profundamente arraigadas de tais transformações são obtidas nas quais não está mais claro o que está acontecendo.
Ok, vamos deixar como está por enquanto. Basta pegar a cor do pixel desejado na textura selecionada e atribuí-la à variável gl_FragColor . Então Nós já fizemos isso? E então este gato aparece novamente. Você não pode usar um não-constante ao acessar uma matriz. E tudo o que calculamos não é mais uma constante. Ba-dum-tsss !!!
Você precisa fazer algo assim:
if (texture_index == 0) { gl_FragColor = texture2D(u_textures[0], texture_coord); } else if (texture_index == 1) { gl_FragColor = texture2D(u_textures[1], texture_coord); } else if (texture_index == 2) { gl_FragColor = texture2D(u_textures[2], texture_coord); }
Concordo que esse código é um caminho direto para o govnokod.ru , mas, mesmo assim, é diferente de qualquer maneira. Mesmo a switch-case não está aqui para, pelo menos de alguma forma, enobrecer essa desgraça. Existe realmente outra muleta menos óbvia que resolve o mesmo problema:
for (int i = 0; i < 3; i++) { if (texture_index == i) { gl_FragColor = texture2D(u_textures[i], texture_coord); } }
Contadores de ciclo, que aumentam em um, o compilador pode contar como uma constante. Mas isso não funcionou com uma variedade de texturas - no último Chrome, ocorreu um erro dizendo que era impossível fazer isso com uma variedade de texturas. Com uma série de números, funcionou. Adivinha por que funciona com uma matriz, mas não com outra? Se você pensou que o sistema de conversão de tipos em JS estava cheio de magia - resolva o sistema "constante - não constante" no GLSL. O engraçado é que os resultados também dependem da placa de vídeo usada, portanto, as muletas complicadas que funcionavam na placa de vídeo NVIDIA podem muito bem quebrar a AMD.
É melhor evitar essas decisões com base em suposições sobre o compilador. Eles tendem a quebrar e são difíceis de testar.
Tristeza é tristeza. Mas, se queremos fazer coisas interessantes, precisamos abstrair tudo isso e continuar.
No momento, temos um mosaico de fotos. Mas há um detalhe: se os pontos se aproximam muito, há uma transição rápida de duas áreas. Não é muito bonito. Você precisa adicionar um algoritmo que não permita que os pontos se aproximem. Você pode fazer uma opção simples, na qual as distâncias entre os pontos são verificadas e, se for menor que um determinado valor, então as separamos. Essa opção não apresenta desvantagens, em particular, às vezes leva a um pequeno tremor nos pontos, mas em muitos casos pode ser suficiente, principalmente porque não há muitos cálculos aqui. Opções mais avançadas seriam um sistema de cargas móveis e uma "teia de aranha" na qual pares de pontos são conectados por fontes invisíveis. Se você estiver interessado em implementá-las, poderá encontrar facilmente todas as fórmulas no livro de referência de física do ensino médio.
for (let i = 0; i < NUMBER_OF_POINTS; i++) { for (let j = i; j < NUMBER_OF_POINTS; j++) { let deltaX = POINTS[i][0] - POINTS[j][0]; let deltaY = POINTS[i][1] - POINTS[j][1]; let distance = Math.sqrt(deltaX * deltaX + deltaY * deltaY); if (distance < 0.1) { POINTS[i][0] += 0.001 * Math.sign(deltaX); POINTS[i][1] += 0.001 * Math.sign(deltaY); POINTS[j][0] -= 0.001 * Math.sign(deltaX); POINTS[j][1] -= 0.001 * Math.sign(deltaY); } } }
O principal problema dessa abordagem, bem como o que usamos no shader, é comparar todos os pontos com todos. Você não precisa ser um grande matemático para entender que o número de cálculos de distância será incrível se não fizermos 10 pontos, mas 1000. Sim, até 100 são suficientes para que tudo diminua a velocidade. Portanto, faz sentido aplicá-lo apenas a um pequeno número de pontos.
Se queremos fazer esse mosaico para um grande número de pontos, podemos usar a divisão familiar do plano em quadrados idênticos. A idéia é colocar um ponto em cada quadrado e realizar todas as comparações apenas com pontos de quadrados vizinhos. Uma boa idéia, mas os experimentos mostraram que, com um grande número de pontos, laptops baratos com placas de vídeo integradas ainda não conseguem lidar. Portanto, vale a pena pensar dez vezes antes de decidir fazer esse mosaico em seu site a partir de um grande número de fragmentos.
Não seja rabanete, verifique o desempenho de seus trabalhos não apenas em sua fazenda de mineração, mas também em laptops comuns. Usuários serão basicamente os únicos.
Particionando um plano de acordo com um gráfico de funções
Vamos ver outra opção para dividir um plano em partes. Não será mais necessário grande poder de computação. A idéia principal é pegar algumas funções matemáticas e construir seu gráfico. A linha resultante apenas dividirá o plano em duas partes. Se usarmos uma função da forma y = f(x) , obteremos a divisão na forma de um corte. Substituindo X por Y, podemos alterar a seção horizontal para vertical. Se você assumir a função em coordenadas polares, precisará traduzir tudo em cartesiano e vice-versa, mas a essência dos cálculos não será alterada. Nesse caso, o resultado não é um corte em duas partes, mas um corte de furo. Mas veremos a primeira opção.
Para cada Y, calcularemos o valor de X para fazer uma seção vertical. Poderíamos pegar uma onda senoidal para esses propósitos, por exemplo, mas é muito chato. É melhor pegar alguns pedaços de uma só vez e dobrá-los.
Tomamos vários sinusóides, cada um deles vinculado a uma coordenada ao longo de Y e ao tempo, e os adicionamos. Os físicos chamariam essa adição de superposição. Obviamente, multiplicando o resultado inteiro por algum número, alteramos a amplitude. Retire-o em uma macro separada. Se você multiplicar a coordenada - o parâmetro seno, a frequência mudará. Já vimos isso em um artigo anterior. Também removemos o modificador de frequência comum a todos os sinusóides da fórmula. Não será supérfluo jogar com o tempo; um sinal negativo dará o efeito de mover a linha na direção oposta.
float time = u_time * SPEED; float x = (sin(texture_coord.y * FREQUENCY) + sin(texture_coord.y * FREQUENCY * 2.1 + time) + sin(texture_coord.y * FREQUENCY * 1.72 + time * 1.121) + sin(texture_coord.y * FREQUENCY * 2.221 + time * 0.437) + sin(texture_coord.y * FREQUENCY * 3.1122 + time * 4.269)) * AMPLITUDE;
Depois de definir essas configurações globais para nossa função, enfrentaremos o problema de repetir o mesmo movimento em intervalos bastante curtos. Para resolver esse problema, precisamos multiplicar tudo por coeficientes para os quais o menor múltiplo comum é muito grande. Algo semelhante também é usado no gerador de números aleatórios, lembra? Nesse caso, não pensamos e pegamos números prontos de algum exemplo da Internet, mas ninguém se incomoda em experimentar nossos valores.
Resta apenas escolher uma das duas texturas para pontos acima do nosso gráfico de funções e a segunda para os pontos abaixo dele. Mais precisamente à esquerda e à direita, todos nos viramos:
if (texture_coord.x - 0.5 > x) { gl_FragColor = texture2D(u_textures[0], texture_coord); } else { gl_FragColor = texture2D(u_textures[1], texture_coord); }
O que recebemos se assemelha a ondas sonoras. Mais precisamente, sua imagem no osciloscópio. De fato, em vez de nossos sinusóides poderíamos transmitir dados de algum tipo de arquivo de som. Mas trabalhar com som é um tópico para um artigo separado.
Máscaras
Os exemplos anteriores devem levar a uma observação bastante lógica: tudo isso se parece com o trabalho de máscaras no SVG (se você não trabalhou com eles, veja exemplos no artigo máscaras SVG e efeitos uau ). Só que aqui nós os fazemos de maneira um pouco diferente. E o resultado é o mesmo - algumas áreas são pintadas com uma textura, outras com outra. Apenas transições suaves ainda não foram. Então vamos fazer um.
Nós removemos todos os desnecessários e retornamos as coordenadas do mouse. Faça um gradiente radial com o centro na localização do cursor e use-o como uma máscara. Neste exemplo, o comportamento do sombreador se assemelhará mais à lógica das máscaras no SVG do que nos exemplos anteriores. Precisamos de uma função de mix e alguma função de distância. A primeira mistura os valores das cores dos pixels das duas texturas, tomando como terceiro parâmetro um coeficiente (de 0 a 1) que determina qual dos valores prevalecerá como resultado. Tomamos o módulo seno em função da distância - ele fornecerá apenas uma mudança suave no valor entre 0 e 1.
gl_FragColor = mix( texture2D(u_textures[0], texture_coord), texture2D(u_textures[1], texture_coord), abs(sin(length(texture_coord - u_mouse_position / u_canvas_size))))
Só isso. Vejamos o resultado:
A principal vantagem sobre o SVG é óbvia:
Ao contrário do SVG, aqui podemos facilmente fazer gradientes suaves para várias funções matemáticas, e não coletá-los de muitos gradientes lineares.
Se você tiver uma tarefa mais simples que não exija transições suaves ou formulários complexos calculados no processo, provavelmente será mais fácil implementar sem o uso de shaders. Sim, e o desempenho em hardware fraco provavelmente será melhor. Escolha uma ferramenta com base em suas tarefas.
Para fins educacionais, vamos ver outro exemplo. Primeiro, faça um círculo no qual a textura permanecerá como está:
gl_FragColor = texture2D(u_textures[0], texture_coord); float dist = distance(texture_coord, u_mouse_position / u_canvas_size); if (dist < 0.3) { return; }
E preencha o resto com listras diagonais:
float value = sin((texture_coord.y - texture_coord.x) * 200.0); if (value > 0.0) { gl_FragColor.rgb *= dist; } else { gl_FragColor.rgb *= dist / 10.0; }
As aceitações são as mesmas - multiplicamos o parâmetro para o seno para aumentar a frequência das faixas; divida os valores obtidos em duas partes; para cada uma das metades, transformamos a cor dos pixels à nossa maneira. É útil lembrar que o desenho de linhas diagonais geralmente está associado à adição de coordenadas em X e Y. Observe que também usamos a distância do cursor do mouse ao alterar as cores, criando assim um tipo de sombra. Da mesma forma, você pode usá-lo com transformações geométricas, em breve veremos isso no exemplo da pixelização. Enquanto isso, dê uma olhada no resultado desse shader:
Simples e bonito.
E sim, se você ficar um pouco confuso, poderá criar texturas não a partir de imagens, mas a partir de quadros de vídeos (existem muitos exemplos na rede, você pode facilmente descobrir) e aplicar todos os nossos efeitos a eles. Muitos sites de diretório como o Awwwards usam esses efeitos em conjunto com o vídeo.
Vale lembrar mais um pensamento:
Ninguém se incomoda em usar uma das texturas como máscara. Podemos tirar uma foto e usar os valores de cores de seus pixels em nossas transformações, sejam mudanças em outras cores, mudanças para os lados ou qualquer outra coisa que lhe vier à mente.
Mas voltando a dividir o avião em partes.
Pixelização
Esse efeito é um tanto óbvio, mas ao mesmo tempo é tão comum que seria errado passar por aqui. Divida nosso plano em quadrados, da mesma maneira que no exemplo com o gerador de ruído e, em seguida, para todos os pixels dentro de cada quadrado, definimos a mesma cor. É obtido através da mistura de valores dos cantos de um quadrado, já fizemos algo semelhante. Para esse efeito, não precisamos de fórmulas complexas, portanto, some todos os valores e divida por 4 - o número de ângulos do quadrado.
float block_size = abs(sin(u_time)) / 20.0; vec2 block_position = floor(texture_coord / block_size) * block_size; gl_FragColor = ( texture2D(u_textures[0], block_position) + texture2D(u_textures[0], block_position + vec2(1.0, 0.0) * block_size) + texture2D(u_textures[0], block_position + vec2(0.0, 1.0) * block_size) + texture2D(u_textures[0], block_position + vec2(1.0, 1.0) * block_size) ) / 4.0;
Novamente, amarramos um dos parâmetros ao tempo no módulo senoidal para ver visualmente o que acontece quando ele muda.
Ondas de pixel
, .
float block_size = abs(sin( length(texture_coord - u_mouse_position / u_canvas_size) * 2.0 - u_time)) / 100.0 + 0.001;
, 0 1; , , , . , .
"" , , -. . " ", , . . — . .
Sumário
, , , , . -. - - . . . , , , .
PS: , WebGL ( ) ? , , . ?