Qual é a ideia de ordenar por escolha?

1. Em um sub-arranjo não classificado, é procurado um máximo local (mínimo).
2. O máximo encontrado (mínimo) muda de lugar com o último (primeiro) elemento na sub-matriz.
3. Se subarrays não classificados permanecerem na matriz, consulte o ponto 1.

Uma ligeira digressão lírica. Inicialmente, em minha série de artigos, planejava apresentar consistentemente o material sobre classificação de classes em uma ordem estrita. Após a classificação da biblioteca , foram planejados artigos sobre outros algoritmos de inserção: classificação de paciência, classificação por uma tabela Young, classificação por inversão, etc.

No entanto, agora a tendência é de não linearidade, portanto, sem escrever todas as publicações sobre classificação por inserções, hoje começarei um ramo paralelo sobre a classificação por seleção. Depois, farei o mesmo com outras classes algorítmicas: classificações de mesclagem, classificações de distribuição etc. Isso geralmente permitirá que as publicações sejam escritas em um tópico e depois em outro. Com essa rotação temática será mais divertido.

Classificação da seleção

Simples e despretensioso - percorremos a matriz em busca do elemento máximo. O máximo encontrado é trocado pelo último elemento. A parte não classificada da matriz diminuiu um elemento (não inclui o último elemento em que reorganizamos o máximo encontrado). Aplicamos as mesmas ações a essa parte não classificada - encontramos o máximo e o colocamos em último lugar na parte não classificada da matriz. E assim continuamos até que a parte não classificada da matriz seja reduzida a um elemento.

def selection(data): for i, e in enumerate(data): mn = min(range(i, len(data)), key=data.__getitem__) data[i], data[mn] = data[mn], e return data 

Classificar com uma escolha simples é uma pesquisa dupla aproximada. Pode ser melhorado? Vejamos algumas modificações.

Classificação de dupla seleção :: Classificação de dupla seleção

Uma idéia semelhante é usada na classificação de shaker , que é uma variante da classificação de bolhas. Passando pela parte não classificada da matriz, além do máximo, também encontramos simultaneamente o mínimo. Colocamos o mínimo em primeiro lugar, o máximo em último. Assim, a parte não classificada em cada iteração é reduzida em dois elementos ao mesmo tempo.

À primeira vista, parece que isso acelera o algoritmo em 2 vezes - após cada passagem, o subarray não classificado é reduzido não de um, mas de dois lados ao mesmo tempo. Mas, ao mesmo tempo, o número de comparações aumentou duas vezes e o número de swaps permaneceu inalterado. A seleção dupla apenas aumenta um pouco a velocidade do algoritmo e, em alguns idiomas, funciona até mais devagar por algum motivo.

A diferença entre classificação por escolha e classificação por inserção

Pode parecer que ordenar por seleção e ordenar por inserções é a mesma coisa, uma classe comum de algoritmos. Bem, ou classificar por inserções é um tipo de classificação por opção. Ou a classificação por opção é um caso especial de classificação por inserções. E aqui e ali, revezamos a parte não classificada da matriz para extrair os elementos e redirecioná-los para a área classificada.

A principal diferença: na classificação por inserções, extraímos qualquer elemento da parte não classificada da matriz e o inserimos em seu lugar na parte classificada. Na classificação por seleção, procuramos propositadamente o elemento máximo (ou mínimo) com o qual complementamos a parte classificada da matriz. Nas inserções, procuramos onde inserir o próximo elemento e na seleção - já sabemos com antecedência qual local colocaremos, mas, ao mesmo tempo, precisamos encontrar o elemento que corresponde a esse local.

Isso torna as duas classes de algoritmos completamente diferentes uma da outra em sua essência e nos métodos usados.

Classificação do Bingo :: Classificação do Bingo

Uma característica interessante das opções de classificação é a independência da velocidade da natureza dos dados que estão sendo classificados.

Por exemplo, se a matriz estiver quase classificada, então, como você sabe, a classificação por inserções a processará muito mais rapidamente (ainda mais rápido que a classificação rápida). Uma matriz de ordem inversa para classificar por inserções é um caso degenerado, e classificará o maior tempo possível.

E para classificar por seleção, a ordem parcial ou reversa da matriz não desempenha um papel - ela será processada aproximadamente na mesma velocidade de uma aleatória normal. Além disso, para a classificação clássica, não importa se a matriz consiste em elementos únicos ou repetitivos - isso praticamente não afeta a velocidade.

Mas, em princípio, você pode inventar e modificar o algoritmo para que ele funcione mais rapidamente com alguns conjuntos de dados. Por exemplo, a classificação do bingo leva em consideração se a matriz consiste em repetir elementos.



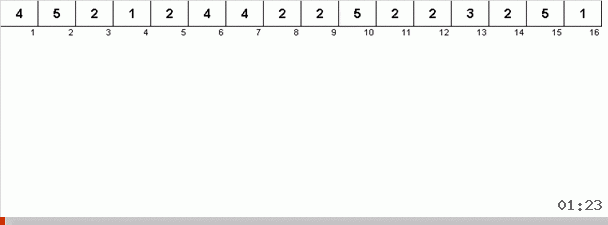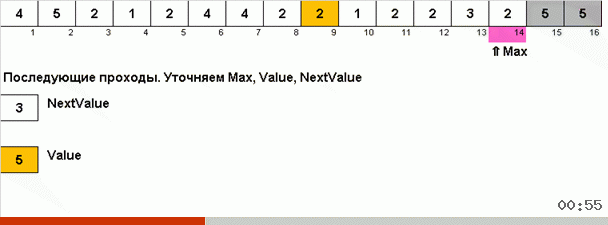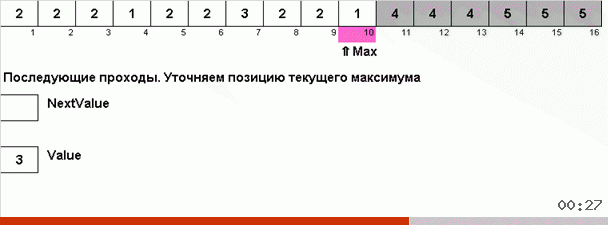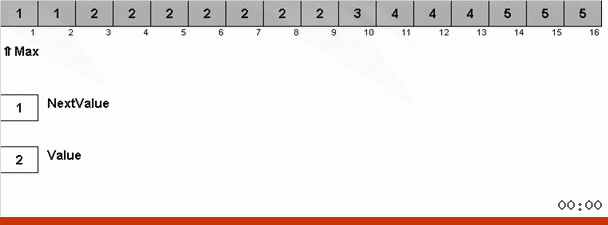
O truque aqui é que não apenas o elemento máximo é lembrado na parte desordenada, mas também é determinado o máximo para a próxima iteração. Isso permite que máximos repetidos não os procurem novamente a cada vez, mas os coloque em seu lugar assim que esse máximo for encontrado novamente na matriz.

A complexidade algorítmica permaneceu a mesma. Mas se a matriz consistir em repetir números, a classificação do bingo lidará dez vezes mais rápido que a classificação normal por opção.

 # - def bingo(data): #  . max = len(data) - 1 nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 #  . while max: value = nextValue nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] == value: data[i], data[max] = data[max], data[i] max -= 1 elif data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 return data 

Classificação do ciclo :: Classificação do ciclo

A classificação de loop é interessante (e valiosa do ponto de vista prático), pois as alterações entre os elementos da matriz ocorrem se, e somente se, o elemento for colocado em seu lugar final. Isso pode ser útil se a reescrita em uma matriz for muito cara e cuidar da memória física exigir minimizar o número de alterações nos elementos da matriz.



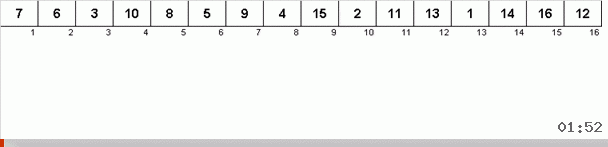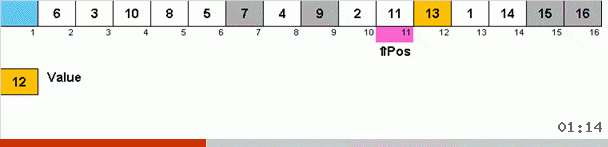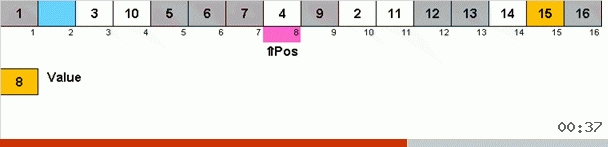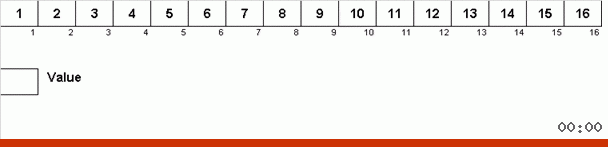
Funciona assim. Classificamos a matriz, chamamos X a próxima célula desse loop externo. E olhamos para qual local da matriz precisamos inserir o próximo elemento dessa célula. No local em que você deseja colar algum outro elemento está localizado, enviamos para a área de transferência. Para esse elemento no buffer, também procuramos seu lugar na matriz (e colamos neste local e enviamos ao buffer o elemento que aparece nesse local). E para o novo número no buffer, realizamos as mesmas ações. Quanto tempo esse processo deve continuar? Até que o próximo elemento da área de transferência seja o elemento que precisa ser inserido com precisão na célula X (o local atual da matriz no loop principal do algoritmo). Cedo ou tarde, esse momento acontecerá e, no loop externo, você poderá ir para a próxima célula e repetir o mesmo procedimento.

Em outros tipos, por opção, procuramos o máximo / mínimo para colocá-los em último / primeiro lugar. No tipo de ciclo, verifica-se que pelo menos o primeiro lugar no subarray está localizado, por assim dizer, no processo de como vários outros elementos são colocados em seus devidos lugares em algum lugar no meio da matriz.

E aqui, a complexidade algorítmica também permanece dentro de O ( n ² ). Na prática, a classificação cíclica funciona até várias vezes mais lenta que a classificação normal por opção, pois você precisa percorrer a matriz mais e comparar com mais frequência. Esse é o preço para o menor número possível de reescritas.

 #   def cycle(data): #        for cycleStart in range(0, len(data) - 1): value = data[cycleStart] # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      ,   #      if pos == cycleStart: continue #   ,     #        while value == data[pos]: pos += 1 data[pos], value = value, data[pos] #      , #         while pos != cycleStart: # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      #      while value == data[pos]: pos += 1 data[pos], value = value, data[pos] return data 

Pancake Sort

Um algoritmo que domina todos os níveis da vida - de bactérias a Bill Gates .



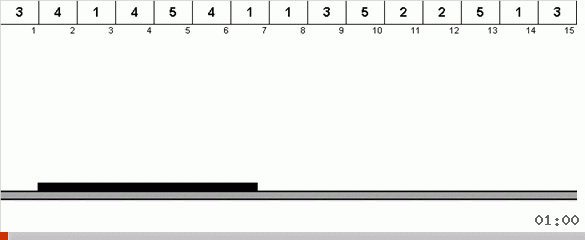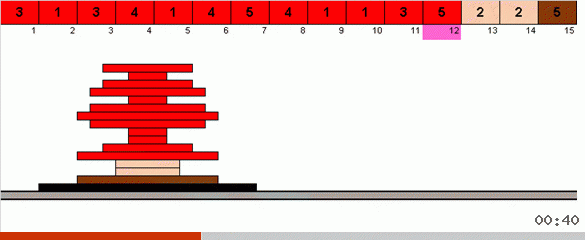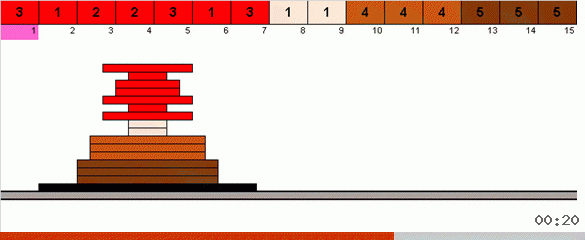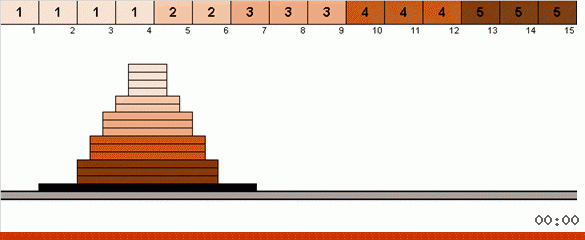
No caso mais simples, estamos procurando o elemento máximo na parte não classificada da matriz. Quando o máximo é encontrado, fazemos duas curvas fechadas. Primeiro, giramos a cadeia de elementos para que o máximo esteja no extremo oposto. Em seguida, viramos todo o sub-arranjo não classificado, como resultado do qual o máximo se encaixa.

Tais cordiletes, de um modo geral, levam à complexidade algorítmica em O ( n ³ ). Esses ciliados treinados estão caindo de uma só vez (portanto, em sua execução, a complexidade é O ( n ² )) e, durante a programação, a reversão de parte da matriz é um ciclo adicional.

A classificação de panquecas é muito interessante do ponto de vista matemático (as melhores mentes pensavam em avaliar o número mínimo de movimentos suficientes para classificar), existem formulações mais complexas do problema (com o chamado lado único queimado). O assunto das panquecas é extremamente interessante, talvez eu escreva uma monografia mais abrangente sobre essas questões.

 #   def pancake(data): if len(data) > 1: for size in range(len(data), 1, -1): #      maxindex = max(range(size), key = data.__getitem__) if maxindex + 1 != size: #    ,    if maxindex != 0: #  , #     data[:maxindex+1] = reversed(data[:maxindex+1]) #    , #      data[:size] = reversed(data[:size]) return data 

---

A classificação por seleção é tão eficaz quanto a busca pelo elemento mínimo / máximo na parte não classificada da matriz. Em todos os algoritmos analisados ​​hoje, a pesquisa é realizada na forma de pesquisa dupla. E na busca dupla, o que quer que se diga, a complexidade algorítmica sempre será melhor que O ( n ² ). Isso significa que todas as classificações por escolha estão fadadas a significar complexidade quadrada? De maneira alguma, se o processo de busca estiver organizado de uma maneira fundamentalmente diferente. Por exemplo, considere um conjunto de dados como um heap e pesquise no heap. No entanto, o tópico de pilhas não é nem um artigo, mas uma saga inteira. Definitivamente falaremos sobre pilhas, mas em outra ocasião.

Referências

Seleção / Ciclo , Panqueca / Panquecas

Artigos da série:

• Aplicativo Excel AlgoLab.xlsm
• Classificações de Câmbio
• Classificações de inserção
• Classificar por seleção
  • Classificação e modificações binárias de heap
  • Classificação binomial e fraca de heap
  • Classificação do Torneio
  • Classificação cartesiana de árvores
  • Classificação da selva
  • Comparando classificações por seleção
• Mesclar classificações
• Classificar por distribuição
• Classificação híbrida

O bingo, o ciclo e a panqueca de hoje foram adicionados ao aplicativo AlgoLab. Neste último, em conexão com o desenho de panquecas, uma restrição foi colocada - os valores dos elementos na matriz devem ser de 1 a 5. É claro que você pode colocar mais, mas as macros receberão aleatoriamente números desse intervalo.