Quanto os dados para o treinamento do modelo (não) são semelhantes a uma amostra de teste?

Considere um cenário em que seu modelo de aprendizado de máquina pode ser inútil.

Há um ditado: "Não compare maçãs com laranjas" . Mas e se você precisar comparar um conjunto de maçãs com laranjas com outro, mas a distribuição de frutas nos dois conjuntos for diferente? Você pode trabalhar com dados? E como você vai fazer isso?


Em casos reais, essa situação é comum. Ao desenvolver modelos de aprendizado de máquina, somos confrontados com uma situação em que nosso modelo funciona bem com um conjunto de treinamento, mas a qualidade do modelo cai acentuadamente nos dados de teste.

E não se trata de reciclagem. Digamos que construímos um modelo que fornece um excelente resultado na validação cruzada, mas mostra um resultado ruim no teste. Portanto, na amostra de teste, há informações que não levamos em consideração.

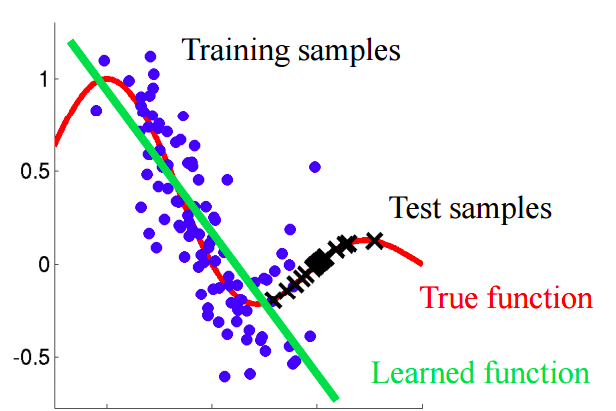
Imagine uma situação em que previmos o comportamento do cliente em uma loja. Se as amostras de treinamento e teste se parecerem com a imagem abaixo, este é um problema claro:


Neste exemplo, o modelo é treinado em dados com um valor médio do atributo "idade do cliente" menor que o valor médio de um atributo semelhante no teste. No processo de aprendizagem, o modelo nunca "viu" os valores maiores do atributo "idade". Se a idade é um recurso importante para o modelo, não se deve esperar bons resultados na amostra de teste.

Neste texto, falaremos sobre abordagens "ingênuas" que nos permitem identificar tais fenômenos e tentar eliminá-los.

Mudança covarde

Vamos dar uma definição mais precisa desse conceito. A covariância refere-se aos valores das características e a mudança covariante refere-se a uma situação em que a distribuição dos valores das características nas amostras de treinamento e teste tem características diferentes (parâmetros).

Em problemas do mundo real com um grande número de variáveis, a mudança covariante é difícil de detectar. O artigo discute o método de identificação e contabilização da mudança covariável nos dados.

Ideia principal

Se houver uma mudança nos dados, ao misturar as duas amostras, podemos construir um classificador que possa determinar se o objeto pertence a uma amostra de treinamento ou teste.


Vamos entender por que isso é assim. Voltemos ao exemplo com os clientes, onde a idade era um sinal "deslocado" das amostras de treinamento e teste. Se pegarmos um classificador (por exemplo, com base em uma floresta aleatória) e tentarmos dividir a amostra mista em treinamento e teste, a idade será um sinal muito importante para essa classificação.

Implementação

Vamos tentar aplicar a ideia descrita a um conjunto de dados real. Use o conjunto de dados da competição Kaggle.

Etapa 1: preparação dos dados

Primeiro, seguiremos uma série de etapas padrão: limpar, preencher os espaços em branco, executar a codificação de etiquetas para sinais categóricos. Nenhuma etapa foi necessária para o conjunto de dados em questão; portanto, pule sua descrição.

import pandas as pd #  train  test train = pd.read_csv('train.csv',low_memory=True) test = pd.read_csv('test.csv',low_memory=True) 

Etapa 2: adicionando um indicador de fonte de dados

É necessário adicionar um novo indicador indicador para ambas as partes do conjunto de dados - treinamento e teste. Para a amostra de treinamento com o valor "1", para o teste, respectivamente, "0".

 #    ,   test,   train test['is_train'] = 0 train['is_train'] = 1 

Etapa 3: Combinando as amostras de aprendizado e teste

Agora você precisa combinar os dois conjuntos de dados. Como o conjunto de dados de treinamento contém uma coluna de valores de destino 'target', que não está no conjunto de dados de teste, essa coluna deve ser excluída.

 #  train, test df_combine = pd.concat([train, test], axis=0, ignore_index=True) #  target df_combine = df_combine.drop('target', axis =1) y = df_combine['is_train'].values #  x = df_combine.drop('is_train', axis=1).values #  tst, trn = test.values, train.values 

Etapa 4: construindo e testando o classificador

Para fins de classificação, usaremos o Random Forest Classifier, que configuraremos para prever os rótulos da fonte de dados no conjunto de dados combinado. Você pode usar qualquer outro classificador.

 from sklearn.ensemble import RandomForestClassifier import numpy as np rfc = RandomForestClassifier(n_jobs=-1, max_depth=5, min_samples_leaf = 5) predictions = np.zeros(y.shape) #     

Utilizamos uma divisão aleatória estratificada de 4 dobras. Dessa forma, manteremos a proporção dos rótulos 'is_train' em cada dobra, como na amostra combinada original. Para cada partição, treinamos o classificador na maioria das partições e prevemos o rótulo da classe para a parte adiada menor.

 from sklearn.model_selection import StratifiedKFold, cross_val_score skf = StratifiedKFold(n_splits=4, shuffle=True, random_state=100) for fold, (train_idx, test_idx) in enumerate(skf.split(x, y)): X_train, X_test = x[train_idx], x[test_idx] y_train, y_test = y[train_idx], y[test_idx] rfc.fit(X_train, y_train) probs = rfc.predict_proba(X_test)[:, 1] #   predictions[test_idx] = probs 

Etapa 5: interpretar os resultados

Calculamos o valor da métrica ROC AUC para nosso classificador. Com base nesse valor, concluímos quão bem nosso classificador revela uma mudança covariável nos dados.

Se o classificador c separar bem os objetos nos conjuntos de dados de treinamento e teste, o valor da métrica ROC AUC deve ser significativamente maior que 0,5, idealmente próximo de 1. Essa imagem indica uma forte mudança covariável nos dados.

Encontre o valor de ROC AUC:

 from sklearn.metrics import roc_auc_score print('ROC-AUC:', roc_auc_score(y_true=y, y_score=predictions)) # ROC-AUC: 0.49974692698385287 

O valor resultante é próximo a 0,5. E isso significa que nosso classificador de qualidade é o mesmo que um preditor de tag aleatório. Não há evidências de uma mudança covariante nos dados.

Como o conjunto de dados é retirado do Kaggle, o resultado é bastante previsível. Como em outras competições de aprendizado de máquina, os dados são cuidadosamente verificados para garantir que não haja turnos.

Mas essa abordagem pode ser aplicada em outros problemas da ciência de dados para verificar a presença de uma mudança covariante imediatamente antes do início da solução.

Passos adicionais

Então, ou observamos uma mudança covariante ou não. O que fazer para melhorar a qualidade do modelo no teste?

1. Remover recursos tendenciosos
2. Usar pesos de importância do objeto com base em estimativas do coeficiente de densidade

Removendo recursos tendenciosos:

Nota: o método é aplicável se houver uma mudança covariante nos dados.

• Extraia a importância dos atributos do Random Forest Classifier, que construímos e treinamos anteriormente.
• Os sinais mais importantes são precisamente aqueles que são tendenciosos e causam uma mudança nos dados.
• Começando pelo mais importante, exclua de uma só vez, construa o modelo de destino e verifique sua qualidade. Colete todos os sinais para os quais a qualidade do modelo não diminui.
• Descarte as características coletadas dos dados e construa o modelo final.

Esse algoritmo permite remover sinais da cesta vermelha no diagrama.

Usando pesos de importância de objeto com base em estimativas do coeficiente de densidade

Nota: o método é aplicável independentemente de haver uma mudança covariante nos dados.

Vejamos as previsões que recebemos na seção anterior. Para cada objeto, a previsão contém a probabilidade de esse objeto pertencer ao conjunto de treinamento do nosso classificador.

 predictions[:10] #array([0.39743827 ... 

Por exemplo, para o primeiro objeto, nosso Classificador Aleatório de Floresta acredita que ele pertence ao conjunto de treinamento com uma probabilidade de 0,397. Chame esse valor $$$P (trem)$. Ou podemos dizer que a probabilidade de pertencer aos dados de teste é de 0,603. Da mesma forma, chamamos de probabilidade $$$P (teste)$.

Agora, um pequeno truque: para cada objeto do conjunto de dados de treinamento, calculamos o coeficiente $$$w = \ frac {P (teste)} {P (trem)}$.

Coeficiente $$$w$nos diz a que distância um objeto do conjunto de treinamento está para testar dados. A ideia principal:

Nós podemos usar $$$w$como pesos em qualquer um dos modelos para aumentar o peso dessas observações que se parecem com a amostra de teste. Intuitivamente, isso faz sentido, já que nosso modelo será mais orientado a dados como em um conjunto de testes.

Esses pesos podem ser calculados usando o código:

 import seaborn as sns import matplotlib.pyplot as plt plt.figure(figsize=(20,10)) predictions_train = predictions[:len(trn)] weights = (1./predictions_train) - 1. weights /= np.mean(weights) #  plt.xlabel('  w') plt.ylabel(' ') sns.distplot(weights, kde=False) 

Os coeficientes obtidos podem ser transferidos para o modelo, por exemplo, da seguinte maneira:

 rfc = RandomForestClassifier(n_jobs=-1,max_depth=5) m.fit(X_train, y_train, sample_weight=weights) 

Algumas palavras sobre o histograma resultante:

• Valores maiores de peso correspondem a observações mais semelhantes à amostra de teste.
• Quase 70% dos objetos do conjunto de treinamento têm um peso próximo a 1 e, portanto, estão localizados em um subespaço semelhante ao conjunto de treinamento e conjunto de teste. Isso corresponde ao valor da AUC que calculamos anteriormente.

Conclusão

Esperamos que este post o ajude a identificar a "mudança covariante" nos dados e combatê-los.

Referências

[1] Shimodaira, H. (2000). Melhorando a inferência preditiva sob mudança covariável, ponderando a função log-verossimilhança. Jornal de Planejamento Estatístico e Inferência, 90, 227-244.
[2] Bickel, S. et al. (2009). Aprendizagem Discriminativa Sob Turno Covariado. Journal of Machine Learning Research, 10, 2137–2155
[3] github.com/erlendd/covariate-shift-adaption
[4] Link para o conjunto de dados usado

PS O laptop com o código do artigo pode ser visto aqui .