Richard Hamming: Capítulo 13. Teoria da Informação

Nós conseguimos!

"O objetivo deste curso é prepará-lo para o seu futuro técnico."

Oi Habr. Lembre-se do incrível artigo "Você e seu trabalho" (+219, 2588 marcado, 429k leituras)?

Portanto, Hamming (sim, sim, códigos de Hamming com auto-verificação e auto-correção) tem um livro inteiro escrito com base em suas palestras. Estamos traduzindo, porque o homem está falando de negócios.

Este livro não é apenas sobre TI, é um livro sobre o estilo de pensamento de pessoas incrivelmente legais. “Isso não é apenas uma carga de pensamento positivo; descreve condições que aumentam as chances de fazer um ótimo trabalho. ”

Obrigado pela tradução para Andrei Pakhomov.

A Teoria da Informação foi desenvolvida por C.E. Shannon no final da década de 1940. A gerência do Bell Labs insistiu que ele a chamasse de "Teoria da Comunicação", porque esse é um nome muito mais preciso. Por razões óbvias, o nome "Teoria da Informação" tem um impacto significativamente maior no público, então Shannon o escolheu, e é o que sabemos até hoje. O próprio nome sugere que a teoria lida com informações, o que a torna importante, pois estamos penetrando mais profundamente na era da informação. Neste capítulo, abordarei algumas conclusões básicas dessa teoria, darei evidências não estritas, mas intuitivas, de algumas das disposições separadas dessa teoria, para que você entenda o que é a "Teoria da Informação", onde você pode aplicá-la e onde não .

Primeiro de tudo, o que é "informação"? Shannon identifica informações com incerteza. Ele escolheu o logaritmo negativo da probabilidade de um evento como uma medida quantitativa das informações que você recebe quando um evento ocorre com probabilidade p. Por exemplo, se eu lhe disser que o tempo em Los Angeles está nublado, então p está próximo de 1, o que, em geral, não nos fornece muita informação. Mas se eu disser que chove em Monterey em junho, haverá incerteza nesta mensagem e ela conterá mais informações. Um evento confiável não contém nenhuma informação, pois o log 1 = 0.

Vamos nos debruçar sobre isso com mais detalhes. Shannon acreditava que uma medida quantitativa de informação deve ser uma função contínua da probabilidade de um evento p e, para eventos independentes, deve ser aditiva - a quantidade de informação obtida como resultado de dois eventos independentes deve ser igual à quantidade de informação obtida como resultado de um evento conjunto. Por exemplo, o resultado de um lançamento de dados e moedas é geralmente considerado como eventos independentes. Vamos traduzir o que foi dito acima para a linguagem da matemática. Se I (p) é a quantidade de informação contida no evento com probabilidade p, então, para um evento conjunto que consiste em dois eventos independentes x com probabilidade p ₁ e y com probabilidade p ₂ obtemos


(eventos independentes x e y)

Essa é a equação funcional de Cauchy, verdadeira para todos os p ₁ e p2. Para resolver essa equação funcional, suponha que

p ₁ = p ₂ = p,

dá



Se p ₁ = p ² ep ₂ = p, então



etc. Estendendo esse processo usando o método padrão para exponenciais para todos os números racionais m / n, o seguinte é verdadeiro



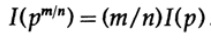
A partir da continuidade assumida da medida de informação, conclui-se que a função logarítmica é a única solução contínua para a equação funcional de Cauchy.

Na teoria da informação, é habitual tomar a base do logaritmo de 2, para que a escolha binária contenha exatamente 1 bit de informação. Portanto, as informações são medidas pela fórmula



Vamos fazer uma pausa e ver o que aconteceu acima. Antes de tudo, não definimos o conceito de “informação”, apenas definimos uma fórmula para sua medida quantitativa.

Em segundo lugar, essa medida depende da incerteza e, embora seja suficientemente adequada para máquinas - por exemplo, sistemas telefônicos, rádio, televisão, computadores etc. - não reflete uma atitude humana normal em relação à informação.

Terceiro, essa é uma medida relativa, depende do estado atual do seu conhecimento. Se você observar o fluxo de "números aleatórios" do gerador de números aleatórios, presume que cada próximo número é indefinido, mas se souber a fórmula para calcular "números aleatórios", o próximo número será conhecido e, portanto, não conterá informação.

Assim, a definição dada por Shannon para informações é, em muitos casos, adequada para máquinas, mas não parece corresponder à compreensão humana da palavra. Por esse motivo, a "Teoria da Informação" deve ser chamada de "Teoria da Comunicação". No entanto, é tarde demais para alterar as definições (graças às quais a teoria ganhou sua popularidade inicial e que ainda faz as pessoas pensarem que essa teoria lida com "informações"), então temos que atendê-las, mas você precisa entender claramente até que ponto a definição de informação dada por Shannon está longe de seu senso comum. As informações de Shannon lidam com algo completamente diferente, a saber, incerteza.

É nisso que você precisa pensar quando oferece alguma terminologia. Quão consistente é a definição proposta, por exemplo, a definição dada por Shannon, com a sua ideia original e qual a diferença? Quase não existe um termo que reflita com precisão sua visão anterior do conceito, mas, no final, é a terminologia usada que reflete o significado do conceito; portanto, formalizar algo através de definições claras sempre faz algum barulho.

Considere um sistema cujo alfabeto consiste em símbolos q com probabilidades pi. Nesse caso, a quantidade média de informações no sistema (seu valor esperado) é:



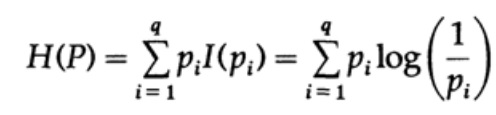
Isso é chamado de entropia do sistema de distribuição de probabilidade {pi}. Usamos o termo “entropia” porque a mesma forma matemática surge na termodinâmica e na mecânica estatística. É por isso que o termo "entropia" cria em torno de si uma aura de importância, que, em última análise, não se justifica. A mesma forma matemática de notação não implica a mesma interpretação de caracteres!

A entropia da distribuição de probabilidade desempenha um papel importante na teoria da codificação. A desigualdade de Gibbs para duas distribuições de probabilidade diferentes pi e qi é uma das consequências importantes dessa teoria. Então temos que provar que



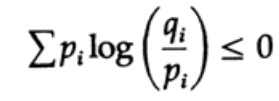
A prova é baseada em um gráfico óbvio, fig. 13.I, que mostra que



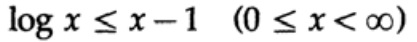
e a igualdade é alcançada apenas para x = 1. Aplicamos a desigualdade a cada soma da soma do lado esquerdo:



Se o alfabeto do sistema de comunicação consiste em q caracteres, pegando a probabilidade de transmissão de cada caractere qi = 1 / q e substituindo q, obtemos da desigualdade de Gibbs





Figura 13.I

Isso sugere que, se a probabilidade de transmitir todos os caracteres q for igual e igual a -1 / q, a entropia máxima será ln q; caso contrário, a desigualdade será mantida.

No caso de um código decodificado exclusivamente, temos a desigualdade Kraft



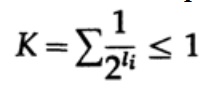
Agora, se definirmos pseudo-probabilidades



onde é claro = 1, que decorre da desigualdade de Gibbs,



e aplicar alguma álgebra (lembre-se de que K ≤ 1, para que possamos omitir o termo logarítmico e, possivelmente, fortalecer a desigualdade posteriormente), obtemos



onde L é o comprimento médio do código.

Assim, entropia é o limite mínimo para qualquer código de caractere com uma palavra de código média L. Esse é o teorema de Shannon para um canal sem interferência.

Agora, consideramos o principal teorema das limitações dos sistemas de comunicação nos quais a informação é transmitida na forma de um fluxo de bits e ruídos independentes. Supõe-se que a probabilidade da transmissão correta de um bit seja P> 1/2 e a probabilidade de o valor do bit ser invertido durante a transmissão (ocorre um erro) é Q = 1 - P. Por conveniência, assumimos que os erros são independentes e a probabilidade de erro é a mesma para cada envio bits - ou seja, há "ruído branco" no canal de comunicação.

A maneira como temos um longo fluxo de n bits codificados em uma única mensagem é uma extensão n-dimensional de um código de um bit. Determinaremos o valor de n posteriormente. Considere uma mensagem que consiste em n bits como um ponto no espaço n dimensional. Como temos um espaço n-dimensional - e por simplicidade, assumimos que cada mensagem tem a mesma probabilidade de ocorrência - existem M mensagens possíveis (M também será determinado posteriormente), portanto, a probabilidade de qualquer mensagem enviada é igual a




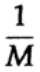
(remetente)
Quadro 13.II

Em seguida, considere a idéia de largura de banda do canal. Sem entrar em detalhes, a capacidade do canal é definida como a quantidade máxima de informações que podem ser transmitidas com segurança pelo canal de comunicação, levando em consideração o uso da codificação mais eficiente. Não há argumento de que mais informações possam ser transmitidas através do canal de comunicação do que sua capacidade. Isso pode ser provado para um canal simétrico binário (que usamos no nosso caso). A capacidade do canal para envio bit a bit é definida como



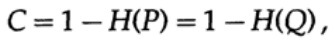
onde, como antes, P é a probabilidade de não haver erro em nenhum bit enviado. Ao enviar n bits independentes, a capacidade do canal é determinada como



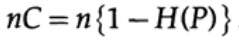
Se estivermos próximos da largura de banda do canal, devemos enviar quase um volume de informações para cada um dos caracteres ai, i = 1, ..., M. Dado que a probabilidade de ocorrência de cada caractere ai é 1 / M, obtemos



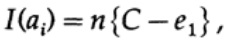
quando enviamos qualquer uma das M mensagens equiprobáveis ​​ai, temos



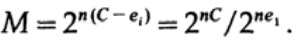
Ao enviar n bits, esperamos que ocorram erros nQ. Na prática, para uma mensagem que consiste em n bits, teremos aproximadamente nQ erros na mensagem recebida. Para n grande, variação relativa (variação = largura da distribuição)
a distribuição do número de erros será mais estreita com o aumento de n.

Então, do lado do transmissor, eu pego a mensagem ai para enviar e desenhar uma esfera ao redor com um raio



que é um pouco maior em uma quantidade igual a e2 do que o número esperado de erros Q (Figura 13.II). Se n for grande o suficiente, haverá uma probabilidade arbitrariamente pequena da aparência do ponto de mensagem bj no lado do receptor, que vai além dessa esfera. Vamos traçar a situação, como eu a vejo do ponto de vista do transmissor: temos quaisquer raios da mensagem transmitida ai para a mensagem recebida bj com uma probabilidade de erro igual a (ou quase igual a) a distribuição normal, atingindo um máximo em nQ. Para qualquer e2, n é tão grande que a probabilidade de que o ponto resultante bj, indo além da minha esfera, seja tão pequena quanto você desejar.

Agora considere a mesma situação de sua parte (Fig. 13.III). No lado do receptor, existe uma esfera S (r) do mesmo raio r em torno do ponto recebido bj no espaço n-dimensional, de modo que se a mensagem recebida bj estiver dentro da minha esfera, a mensagem que eu enviei estará dentro da sua esfera.

Como pode ocorrer um erro? Pode ocorrer um erro nos casos descritos na tabela abaixo:



Figura 13.III



Aqui vemos que, se na esfera construída em torno do ponto recebido, houver pelo menos mais um ponto correspondente a uma possível mensagem não codificada enviada, ocorreu um erro durante a transmissão, pois você não pode determinar qual dessas mensagens foi transmitida. A mensagem enviada não contém erros apenas se o ponto correspondente a ela estiver na esfera e não houver outros pontos possíveis neste código que estejam na mesma esfera.

Temos uma equação matemática para a probabilidade de um erro Re se ai foi enviado



Podemos jogar fora o primeiro fator no segundo mandato, tomando-o como 1. Assim, obtemos a desigualdade



Obviamente,



portanto



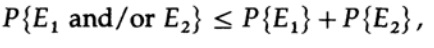
reaplicar ao último membro à direita



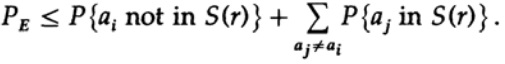
Se n for tomado em tamanho suficiente, o primeiro termo poderá ser arbitrariamente pequeno, digamos, menor que um determinado número d. Portanto, temos



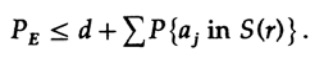
Agora vamos ver como você pode criar um código de substituição simples para codificar M mensagens consistindo em n bits. Não tendo idéia de como criar o código (os códigos de correção de erros ainda não foram inventados), Shannon escolheu a codificação aleatória. Jogue uma moeda para cada um dos n bits da mensagem e repita o processo para M mensagens. Tudo o que você precisa fazer é o sorteio de moedas nM, para que seja possível



dicionários de código com a mesma probabilidade de ½nM. Obviamente, o processo aleatório de criação de um livro de códigos significa que há uma probabilidade de duplicatas, bem como pontos de código, que estarão próximos um do outro e, portanto, serão uma fonte de erros prováveis. É necessário provar que, se isso não ocorrer com uma probabilidade maior que qualquer pequeno nível de erro selecionado, o n fornecido será grande o suficiente.
O ponto decisivo é que Shannon calculou a média de todos os livros de códigos possíveis para encontrar o erro médio! Usaremos o símbolo Av [.] Para indicar a média no conjunto de todos os possíveis dicionários de códigos aleatórios. A média sobre a constante d, é claro, fornece uma constante, pois para calcular a média de cada termo coincide com qualquer outro termo na soma



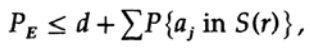
que pode ser aumentado (M - 1 vai para M)



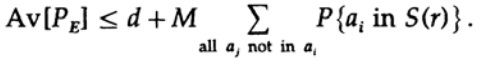
Para qualquer mensagem em particular, ao calcular a média de todos os livros de códigos, a codificação é executada em todos os valores possíveis; portanto, a probabilidade média de um ponto em uma esfera é a razão entre o volume da esfera e o volume total de espaço. O escopo da esfera



onde s = Q + e2 <1/2 e ns deve ser um número inteiro.

O último termo à direita é o maior nesta soma. Primeiro, estimamos seu valor pela fórmula de Stirling para fatoriais. Em seguida, examinamos o coeficiente de redução do termo à sua frente, observe que esse coeficiente aumenta quando se move para a esquerda e, portanto, podemos: (1) limitar o valor da soma à soma da progressão geométrica com esse coeficiente inicial, (2) expandir a progressão geométrica de ns membros para número infinito de termos, (3) calcule a soma da progressão geométrica infinita (álgebra padrão, nada significativo) e, finalmente, obtenha o valor limite (para um n suficientemente grande):



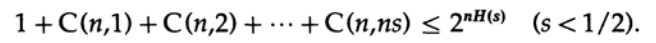
Observe como a entropia H (s) apareceu na identidade binomial. Observe que a expansão nas séries de Taylor H (s) = H (Q + e2) fornece uma estimativa obtida levando em consideração apenas a primeira derivada e ignorando todas as outras. Agora vamos coletar a expressão final:



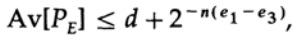
onde



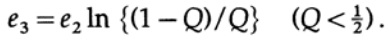
Tudo o que precisamos fazer é escolher e2 para que e3 <e1, e então o último termo seja arbitrariamente pequeno, por n suficientemente grande. Portanto, o erro PE médio pode ser obtido arbitrariamente pequeno com uma capacidade de canal arbitrariamente próxima de C.
Se a média de todos os códigos tiver um erro suficientemente pequeno, pelo menos um código deve ser adequado; portanto, existe pelo menos um sistema de codificação adequado. Esse é um resultado importante obtido por Shannon - “teorema de Shannon para um canal com interferência”, embora deva-se notar que ele o provou para um caso muito mais geral do que para um canal simétrico binário simples que eu usei. Para o caso geral, os cálculos matemáticos são muito mais complicados, mas as idéias não são tão diferentes, com muita frequência, usando o exemplo de um caso especial, pode-se revelar o verdadeiro significado do teorema.

Vamos criticar o resultado. Repetimos repetidamente: "Para n suficientemente grande". Mas quão grande é n? Muito, muito grande, se você realmente deseja estar simultaneamente próximo da largura de banda do canal e garantir a transferência correta de dados! Tão grande que, na verdade, você terá que esperar muito tempo para acumular uma mensagem de tantos bits para codificá-la mais tarde. Nesse caso, o tamanho do dicionário de código aleatório será enorme (afinal, esse dicionário não pode ser representado em uma forma menor que a lista completa de todos os bits Mn, enquanto n e M são muito grandes)!

Os códigos de correção de erros evitam aguardar uma mensagem muito longa, com sua subsequente codificação e decodificação por meio de grandes livros de códigos, porque evitam os livros de códigos em si e, em vez disso, usam cálculos convencionais. Em uma teoria simples, esses códigos, em regra, perdem a capacidade de se aproximar da capacidade do canal e, ao mesmo tempo, mantêm uma taxa de erro razoavelmente baixa, mas quando o código corrige um grande número de erros, eles mostram bons resultados. Em outras palavras, se você está colocando algum tipo de capacidade de canal para correção de erros, deve usar a opção de correção de erros na maioria das vezes, ou seja, em cada mensagem enviada, um grande número de erros deve ser corrigido, caso contrário, você perde essa capacidade em vão.

Além disso, o teorema provado acima ainda não tem sentido! Isso mostra que sistemas de transmissão eficientes devem usar esquemas de codificação sofisticados para sequências de bits muito longas. Um exemplo são os satélites que voaram para fora do planeta exterior; à medida que se afastam da Terra e do Sol, são forçados a corrigir cada vez mais erros no bloco de dados: alguns satélites usam baterias solares, que fornecem cerca de 5 watts, outros usam fontes de energia atômica que fornecem a mesma energia.A fraca potência da fonte de alimentação, o tamanho pequeno das placas transmissoras e o tamanho limitado das placas receptoras na Terra, a grande distância que o sinal deve percorrer - tudo isso requer o uso de códigos com alto nível de correção de erros para construir um sistema de comunicação eficaz.

Voltamos ao espaço n-dimensional que usamos na prova acima. Discutindo isso, mostramos que quase todo o volume da esfera está concentrado perto da superfície externa; portanto, quase certamente o sinal enviado será localizado na superfície da esfera construída em torno do sinal recebido, mesmo com um raio relativamente pequeno dessa esfera. Portanto, não é surpreendente que o sinal recebido após a correção de um número arbitrariamente grande de erros, nQ, seja arbitrariamente próximo do sinal sem erros. A capacidade do canal de comunicação, que examinamos anteriormente, é a chave para entender esse fenômeno. Observe que essas esferas construídas para códigos de correção de erros de Hamming não se sobrepõem. Um grande número de medições praticamente ortogonais no espaço n-dimensional mostrapor que podemos encaixar as esferas M em um espaço com uma leve sobreposição. Se você permitir uma sobreposição pequena e arbitrariamente pequena, o que pode levar apenas a um pequeno número de erros durante a decodificação, você poderá obter um arranjo denso de esferas no espaço. Hamming garantiu um certo nível de correção de erros, Shannon - uma baixa probabilidade de erro, mas ao mesmo tempo mantendo a largura de banda real arbitrariamente próxima da capacidade do canal de comunicação, o que os códigos de Hamming não podem fazer.mas, ao mesmo tempo, a preservação da taxa de transferência real é arbitrariamente próxima da capacidade do canal de comunicação, o que os códigos de Hamming não podem fazer.mas, ao mesmo tempo, a preservação da taxa de transferência real é arbitrariamente próxima da capacidade do canal de comunicação, o que os códigos de Hamming não podem fazer.

A teoria da informação não fala sobre como projetar um sistema eficaz, mas indica a direção do movimento em direção a sistemas de comunicação eficazes. Essa é uma ferramenta valiosa para a construção de sistemas de comunicação entre máquinas, mas, como observado anteriormente, não tem muito a ver com a maneira como as pessoas trocam informações entre si. A extensão em que a herança biológica é semelhante aos sistemas de comunicação técnica é simplesmente desconhecida; portanto, atualmente não está claro como a teoria da informação se aplica aos genes. Não temos escolha a não ser tentar, e se o sucesso nos mostrar a natureza semelhante a uma máquina desse fenômeno, o fracasso apontará para outros aspectos significativos da natureza da informação.

Não vamos nos distrair muito. Vimos que todas as definições iniciais, em maior ou menor grau, deveriam expressar a essência de nossas crenças iniciais, mas são caracterizadas por um certo grau de distorção e, portanto, não são aplicáveis. É tradicionalmente aceito que, em última análise, a definição que usamos define realmente a essência; mas apenas nos diz como processar as coisas e não faz sentido algum. A abordagem postulativa, tão aclamada nos círculos matemáticos, deixa muito a desejar na prática.

Agora, veremos um exemplo de testes de QI, em que a definição é tão cíclica quanto você gosta e, como resultado, o engana. Um teste é criado para medir a inteligência. Depois disso, ele é revisado para ser o mais consistente possível e, em seguida, é publicado e calibrado de maneira simples, para que a "inteligência" medida seja normalmente distribuída (é claro, ao longo da curva de calibração). Todas as definições devem ser cruzadas, não apenas quando são propostas pela primeira vez, mas muito mais tarde, quando são usadas nas conclusões feitas. Até que ponto os limites de definição são adequados para a tarefa em questão? Com que frequência as definições dadas nas mesmas condições começam a ser aplicadas em condições bastante diferentes? Isso é bastante comum!Nas humanidades que você inevitavelmente encontrará em sua vida, isso acontece com mais frequência.

Assim, um dos objetivos desta apresentação da teoria da informação, além de demonstrar sua utilidade, era alertá-lo sobre esse perigo ou demonstrar como usá-lo para obter o resultado desejado. Há muito se nota que as definições iniciais determinam o que você encontra no final, em uma extensão muito maior do que parece. As definições iniciais exigem que você preste muita atenção não apenas em qualquer nova situação, mas também em áreas com as quais você trabalha há muito tempo. Isso permitirá que você entenda até que ponto os resultados obtidos são uma tautologia e não algo útil.

, . , , , ! , .

...

, — magisterludi2016@yandex.ru

, — «The Dream Machine: » )

, , . ( 10 , 20 )