Esconda sem se esconder. Mais uma vez sobre esteganografia LSB, qui-quadrado e ... singularidade?

Hoje, voltaremos a ativar o ninho antigo e falaremos sobre como esconder um monte de bits na imagem com o gato, examinar várias ferramentas disponíveis e analisar os ataques mais populares. E parece, o que a singularidade tem a ver com isso?

Como se costuma dizer, se você quiser descobrir algo, escreva um artigo sobre isso no Habr! (Cuidado, muito texto e fotos)



Esteganografia (literalmente do grego para "criptografia") - para ocultar a ciência de dados (stegosoobscheniya) em outros dados abertos (stegokonteynerov) por ocultação de transferência de dados. Não se assuste, de fato, nem tudo é tão complicado.

Então, onde na imagem você pode ocultar a mensagem para que ninguém perceba?

E existem apenas dois lugares: metadados e a própria imagem. O último é bastante simples, basta digitar "exif" no Google. Então, vamos começar imediatamente com o segundo.

Bit menos significativo

O modelo de cor mais popular é o RGB, onde a cor é representada na forma de três componentes: vermelho, verde e azul . Cada componente é codificado na versão clássica usando 8 bits, ou seja, pode assumir um valor de 0
para 255. É aqui que o bit menos significativo é oculto. É importante entender que uma dessas cores RGB é responsável por três desses bits.

Para apresentá-los mais claramente, faremos algumas pequenas manipulações.

Como prometido, tire uma foto de um gato em formato png.



Dividimos em três canais e, em cada canal, pegamos o bit menos significativo. Crie três novas imagens, em que cada pixel representa NZB. Zero - o pixel é branco, a unidade é respectivamente preta.

Nós entendemos isso.




Mas, como regra, a imagem é encontrada na "forma montada". Para representar o NZB de três componentes em uma imagem, basta substituir o componente em um pixel em que o NZB é unificado, substitua-o por 255 e substitua-o por 0.

Mas não menos significativo

Imagine que tudo o que vimos na última foto é nosso e temos o direito de fazer qualquer coisa com ele. Então, tomamos isso como um fluxo de bits, de onde podemos ler e onde podemos escrever.

Pegamos os dados que queremos intercalar na imagem, os apresentamos na forma de bits e os anotamos no lugar dos existentes.

Para extrair esses dados, lemos o NZB como um fluxo de bits e o trazemos para a forma desejada. Para descobrir quantos bits precisam ser contados, como regra, o tamanho da mensagem é gravado no início. Mas esses são detalhes de implementação.

Deve-se notar que em cerca de 50% dos casos, o pouco que queremos escrever e o pouco na imagem coincidirão e não precisaremos mudar nada.

Isso é tudo, o método termina aqui.

Por que isso funciona?

Dê uma olhada nas imagens abaixo.

Este é um stegocontainer vazio:



E isso está 95% cheio:



Veja a diferença? Mas ela é. Porque

Vejamos duas cores: (0, 0, 0) e (1, 1, 1), ou seja, cores diferentes apenas pelo NZB em cada componente.



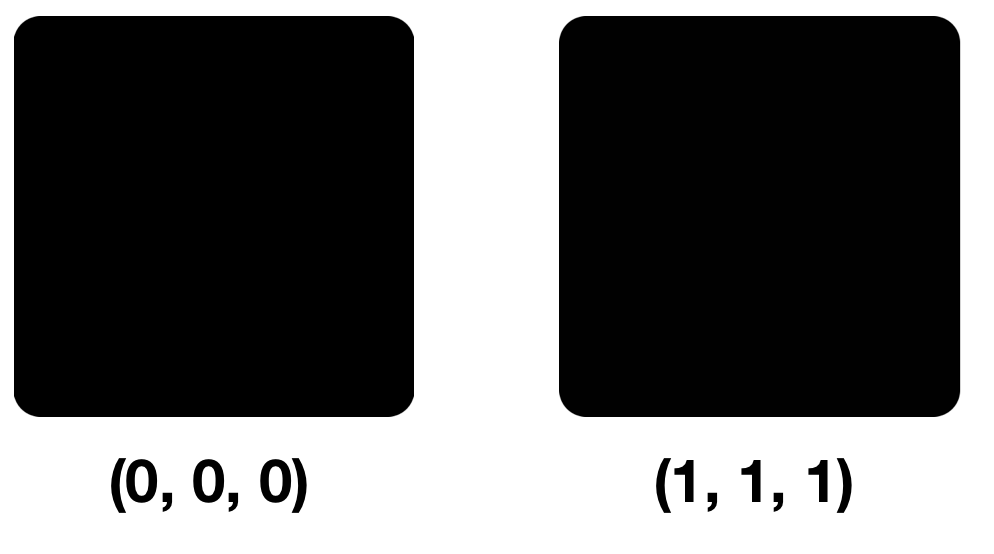
Pequenas diferenças de pixels no primeiro, segundo e terceiro olhares não serão visíveis. O fato é que nossos olhos conseguem distinguir cerca de 10 milhões de cores, e o cérebro tem apenas cerca de 150. O modelo RGB também contém 16.777.216 cores. Você pode tentar diferenciá-los todos aqui.

Na linha de comando

Não há muitas ferramentas de linha de comando de código aberto disponíveis que representem a esteganografia LSB.

O mais popular pode ser encontrado na tabela abaixo.

Cadê o gato?

E o primeiro da lista de ataques à esteganografia do LSB é um ataque visual. Soa estranho, não é? Afinal, o gato com um segredo não se traiu como um stegocontainer cheio à primeira vista. Hmmm ... Você só precisa saber para onde procurar. É fácil adivinhar que apenas o NZB merece nossa atenção.

Para um stegocontainer preenchido, a imagem com o NZB é assim:



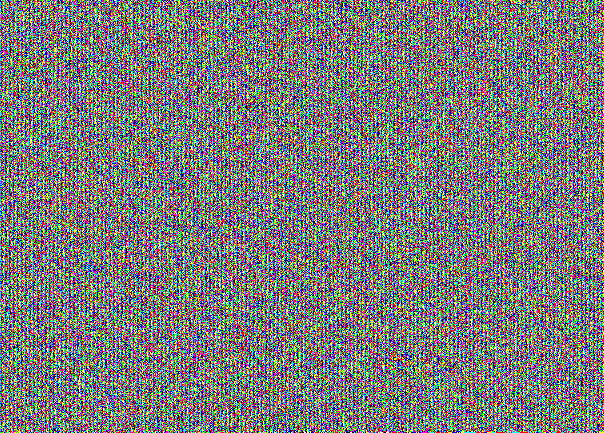
Não acredita? Aqui você tem NZB dos três canais separadamente:




Este é um "desenho" específico para ocultar a mensagem no NZB. À primeira vista, isso parece um barulho simples. Mas ao considerar a estrutura é visível. Aqui você pode ver que o stegocontainer está cheio. Se recebermos uma mensagem com 30% da capacidade de um gato pobre, teremos a seguinte imagem:


Seu NZB:



~ 70% do gato permanece inalterado.

Aqui vale a pena fazer uma pequena digressão e falar sobre tamanhos. O que é um gato de 30%? O tamanho do gato é 603x433 pixels. 30% deste tamanho é 78459 pixels. Cada pixel contém 3 bits de informação. O total de 78459 3 = 235377 bits ou um pouco menos de 30 kilobytes se encaixa em 30% do selo. E no gato inteiro caberá cerca de 100 kilobytes. Essas coisas.

Mas estamos aqui para você por um motivo. Como, então, enganar os olhos?
Primeiro pensamento: coloque a mensagem no barulho. Mas não estava lá. Em seguida, há um fragmento do stegocontainer preenchido e seu LSB.



Com um pouco de esforço, ainda podemos discernir uma estrutura familiar. Não percam a esperança, senhores!

Hee hee hee

Muitas coisas quebram as estatísticas, você sabe.

Mudando algo na imagem, mudamos suas propriedades estatísticas. É o suficiente para o analista encontrar uma maneira de corrigir essas alterações.

O bom e velho qui-quadrado foi iniciado por Andreas Wesfield e Andreas Pfitzmann, da Universidade de Dresden, em seu trabalho "Ataques a sistemas esteganográficos", que pode ser encontrado aqui.

A seguir, falaremos sobre ataques no mesmo plano de cores, ou no contexto de RGB, sobre ataques em um canal. Os resultados de cada ataque podem ser reduzidos à média e obter o resultado para a imagem "montada".

Portanto, o ataque do qui-quadrado baseia-se no pressuposto de que a probabilidade de aparência simultânea de cores vizinhas (diferentes pelo bit menos significativo) (par de valores) em um recipiente vazio é extremamente pequena. É realmente, você pode acreditar. Em outras palavras, o número de pixels de duas cores adjacentes é significativamente diferente para um contêiner vazio. Tudo o que precisamos fazer é calcular o número de pixels de cada cor e aplicar algumas fórmulas. De fato, é uma tarefa simples testar uma hipótese usando o teste do qui-quadrado.

Um pouco de matemática?

Seja h uma matriz no i-ésimo lugar, contendo o número de pixels da i-ésima cor na imagem em estudo.

Então:

1. Frequência de cor medida $$$i = $ 2$ :
   

   $$

   $$n_k = h [2k], ~ k \ em [0, 127];$$
   
   
2. Frequência de cores teórica esperada $$$i = $ 2$ :
   

   $$

   $$n_k ^ * = \ frac {h [2k] + h [2k + 1]} {2}, ~ k \ em [0,127];$$
   
   

Traduzir isso para Python produzirá algo como isto:

for k in range(0, len(histogram) // 2): expected.append(((histogram[2 * k] + histogram[2 * k + 1]) / 2)) observed.append(histogram[2 * k]) 

Onde histograma é o número de pixels da cor i na imagem, $$$i \ em [0, 255]$

O critério qui-quadrado para o número de graus de liberdade k-1 é calculado da seguinte forma (k é o número de cores diferentes, ou seja, 256):

$$

$$\ chi_ {k-1} ^ 2 = \ sum_ {i = 1} ^ {k} \ frac {(n_k - n_k ^ *) ^ 2} {n_k ^ *};$$

E, finalmente, P é a probabilidade de que as distribuições $$$n_i$ e $$$n_i ^ *$ nessas condições, eles são iguais (a probabilidade de termos um recipiente cheio). É calculado integrando a função de suavidade:

$$

$$P = 1 - \ frac {1} {2 ^ {\ frac {k-1} {2}} \ Gamma (\ frac {k-1} {2})} \ int_0 ^ {\ chi_ {k-1 } ^ 2} e ^ {- \ frac {x} {2}} x ^ {\ frac {k-1} {2} -1} dx;$$

É mais eficaz aplicar um qui-quadrado não à imagem inteira, mas apenas às partes, por exemplo, às linhas. Se a probabilidade calculada para a linha for maior que 0,5, preencha a linha na imagem original com vermelho. Se menos, então verde. Para um gato com 30% de plenitude, a imagem terá a seguinte aparência:



Muito certo, não é?

Bem, tivemos um ataque matematicamente sólido, você não pode enganar a matemática! Ou ... ??

Shuffle dance

A idéia é bem simples: escreva bits não em ordem, mas em lugares aleatórios. Para fazer isso, você precisa usar o PRSP, configurá-lo para emitir o mesmo fluxo aleatório com o mesmo lado (também conhecido como senha). Sem saber a senha, não poderemos configurar o PRNG e encontrar os pixels em que a mensagem está oculta. Vamos testá-lo em um gato.

Gatinho (32% de conclusão):



Seu LSB:



A imagem parece barulhenta, mas não suspeita para um analista inexperiente. O que diz o qui-quadrado?


Parece que o chapéu preto ganhou!? Não importa como ...

Regularidade-Singularidade

Outro método estatístico foi Jessica Friedrich, Miroslav Golyan e Andreas Pfitzman em 2001. Foi nomeado como o método RS. O artigo original pode ser obtido aqui.

O método contém várias etapas preparatórias.

A imagem é dividida em grupos de n pixels. Por exemplo, 4 pixels consecutivos seguidos. Como regra, esses grupos contêm pixels adjacentes.
Para o nosso gato com preenchimento sequencial no canal vermelho, os cinco primeiros grupos serão:

• [78, 78, 79, 78]
  
• [78, 78, 78, 78]
  
• [78, 79, 78, 79]
  
• [79, 76, 79, 76]
  
• [76, 76, 76, 77]
  

(Todas as medidas estão na versão clássica do RGB)

Em seguida, definimos a chamada função discriminante ou função de suavidade, que mapeia cada grupo de pixels para um número real. O objetivo desta função é capturar a suavidade ou "regularidade" do grupo de pixels G. Quanto mais ruidoso o grupo de pixels $$$G = (x_1, ..., x_n)$ , mais importante será a função discriminante. Na maioria das vezes, é escolhida uma "variação" de um grupo de pixels ou, mais simplesmente, a soma das diferenças de pixels vizinhos em um grupo. Mas também pode levar em consideração suposições estatísticas sobre a imagem.

$$

$$f (x_1, x_2, ..., x_n) = \ sum_ {i = 1} ^ {n-1} | x_ {i + 1} - x_i |$$

Os valores da suavidade funcionam para um grupo de pixels do nosso exemplo:

• f (78, 78, 79, 78) = 2
• f (78, 78, 78, 78) = 0
• f (78, 79, 78, 79) = 3
• f (79, 76, 79, 76) = 9
• f (76, 76, 76, 77) = 1

Em seguida, é determinada a classe de funções de inversão de um pixel.

Eles devem ter algumas propriedades.

$$

$$1. ~~~ \ forall x \ in P: ~ F (F (x)) = x, ~~ P = \ {0, ~ 255 \};$$

$$

$$2. ~~~ F_1: 0 \ leftrightarrow 1, ~ 2 \ leftrightarrow 3, ~ ..., 254 \ leftrightarrow 255;$$

$$

$$3 ~~~ \ forall x \ in P: ~ F _ {- 1} (x) = F_1 (x + 1) -1;$$

Onde $$$F$ - qualquer função de uma classe, $$$F_1$ É uma função de inversão direta e $$$F _ {- 1}$ - inverter. Além disso, a mesma função de inversão é geralmente indicada $$$F_0$ o que não altera o pixel.

As funções de lançamento de python podem se parecer com isso:

 def flip(val): if val & 1: return val - 1 return val + 1 def invert_flip(val): if val & 1: return val + 1 return val - 1 def null_flip(val): return val 

Para cada grupo de pixels, aplicamos uma das funções de inversão e, com base no valor da função discriminante antes e após a inversão, determinamos o tipo de grupo de pixels: normal ( R egular), único / incomum ( S ingular) e inútil inutilizável. Como o último tipo não é mais usado, o método foi nomeado após as primeiras letras dos tipos de chave. Esse é todo o segredo do nome, a singularidade não tem nada a ver com isso :)



Podemos aplicar diferentes inversões a diferentes pixels, para isso definimos uma máscara M com n valores de -1, 0 ou 1.

$$

$$F_M (G) = (F_ {M (1)} (x_1), F_ {M (2)} (x_2), ..., F_ {M (n)} (x_n))$$

Deixe a máscara do nosso exemplo ser clássica - [1, 0, 0, 1]. Foi experimentalmente encontrado que máscaras simétricas que não contêm $$$F _ {- 1}$ . As opções bem-sucedidas também seriam: [0, 1, 0, 1], [0, 1, 1, 0], [1, 0, 1, 0]. Aplicamos a inversão para os grupos do exemplo, calculamos o valor da suavidade e determinamos o tipo de grupo de pixels:

• $$$F_m$ (78, 78, 79, 78) = [79, 78, 79, 79];
  f (79, 78, 79, 79) = 2 = 2 = f (78, 78, 79, 78)
  Grupo inutilizável
  
  
• $$$F_m$ (78, 78, 78, 78) = [79, 78, 78, 79];
  f (79, 78, 78, 79) = 2> 0 = f (78, 78, 78, 78)
  Grupo regular
  
  
• $$$F_m$ (78, 79, 78, 79) = [79, 79, 78, 78];
  f (79, 79, 78, 78) = 1 <3 = f (78, 79, 78, 79) Grupo singular
  
  
• $$$F_m$ (79, 76, 79, 76) = [78, 76, 79, 77];
  f (78, 76, 79, 77) = 7 <9 = f (79, 76, 79, 76) Grupo singular
  
  
• $$$F_m$ (76, 76, 76, 77) = [77, 76, 76, 76];
  f (77, 76, 76, 76) = 1 = 1 = f (76, 76, 76, 77)
  Grupo inutilizável
  
  

Denotamos o número de grupos regulares para a máscara M como $$$R_M$ (em porcentagens de todos os grupos) e $$$S_M$ para grupos singulares.

Então $$$R_M + S_M \ leq 1$ e $$$R _ {- M} + S _ {- M} \ leq 1$ , para uma máscara negativa (todos os componentes da máscara são multiplicados por -1), porque $$$R_M + S_M + U_M = 1$ enquanto $$$U_M$ pode estar vazio. Da mesma forma para uma máscara negativa.

A principal hipótese estatística é que em uma imagem típica o valor esperado $$$R_M$ igual a $$$R _ {- M}$ , e o mesmo vale para $$$S_M$ e $$$S _ {- M}$ . Isso é comprovado por dados experimentais e algumas danças com um pandeiro em torno da última propriedade da função de inversão.

$$

$$R_M \ cong S_M ~~~~ R _ {- M} \ cong S _ {- M}$$

Vamos dar uma olhada no nosso pequeno exemplo? Dado o pequeno tamanho da amostra, podemos não confirmar esta hipótese. Vamos ver o que acontece com a máscara invertida: [-1, 0, 0, -1].

• F_M (78, 78, 79, 78) = [77, 78, 79, 77];
  f (77, 78, 79, 77) = 4> 2 = f (77, 78, 79, 77)
  Grupo regular
  
  
• F_M (78, 78, 78, 78) = [77, 78, 78, 77];
  f (77, 78, 78, 77) = 2> 0 = f (78, 78, 78, 78)
  Grupo regular
  
  
• F_M (78, 79, 78, 79) = [77, 79, 78, 80];
  f (77, 79, 78, 80) = 5> 3 = f (78, 79, 78, 79)
  Grupo regular
  
  
• F_M (79, 76, 79, 76) = [80, 76, 79, 75];
  f (80, 76, 79, 75) = 11> 9 = f (79, 76, 79, 76)
  Grupo regular
  
  
• F_M (76, 76, 76, 77) = [75, 76, 76, 78];
  f (75, 76, 76, 78) = 3> 1 = f (76, 76, 76, 77)
  Grupo regular
  
  

Bem, tudo é óbvio.

No entanto, a diferença entre $$$R_M$ e $$$S_M$ tendem a zero à medida que o comprimento m da mensagem incorporada aumenta e obtemos esse $$$R_M \ cong S_M$ .

É engraçado que a randomização do plano LSB tenha o efeito oposto sobre $$$R _ {- M}$ e $$$S _ {- M}$ . Sua diferença aumenta com o comprimento m da mensagem incorporada. Uma explicação para esse fenômeno pode ser encontrada no artigo original.

Aqui está a programação $$$R_M$ , $$$S_M$ , $$$R _ {- M}$ e $$$S _ {- M}$ dependendo do número de pixels com LSBs invertidos, é chamado de diagrama RS. O eixo x é a porcentagem de pixels com LSBs invertidos, o eixo y é o número relativo de grupos regulares e singulares com máscaras M e -M, $$$M = [0 ~ 1 ~ 1 ~ 0]$ .



A essência do método de análise de RS é avaliar as quatro curvas do diagrama de RS e calcular sua interseção usando extrapolação. Suponha que tenhamos um stegocontainer com uma mensagem de tamanho desconhecido p (como porcentagem de pixels) incorporada nos bits inferiores dos pixels selecionados aleatoriamente (ou seja, usando RandomLSB). Nossas medições iniciais do número de grupos R e S correspondem a pontos $$$R_M (p / 2)$ , $$$S_M (p / 2)$ , $$$R _ {- M} (p / 2)$ e $$$S _ {- M} (p / 2)$ . Tomamos pontos exatamente da metade do comprimento da mensagem, já que a mensagem é um fluxo de bits aleatório e, em média, como mencionado anteriormente, apenas metade dos pixels será alterada incorporando a mensagem.

Se invertermos o LSB de todos os pixels da imagem e calcularmos o número de grupos R e S, obteremos quatro pontos $$$R_M (1-p / 2)$ , $$$S_M (1-p / 2)$ , $$$R _ {- M} (1-p / 2)$ e $$$S _ {- M} (1-p / 2)$ . Como esses dois pontos dependem da randomização específica do LSB, devemos repetir esse processo várias vezes e avaliar $$$R_M (1/2)$ e $$$S_M (1/2)$ de amostras estatísticas.

Podemos desenhar condicionalmente linhas através de pontos $$$R _ {- M} (p / 2)$ , $$$R _ {- M} (1-p / 2)$ e $$$S _ {- M} (p / 2)$ , $$$S _ {- M} (1-p / 2)$ .

Pontos $$$R_M (p / 2)$ , $$$R_M (1/2)$ , $$$R_M (1-p / 2)$ e $$$S_M (p / 2)$ , $$$S_M (1/2)$ , $$$S_M (1-p / 2)$ defina duas parábolas. Cada parábola e a linha correspondente se cruzam à esquerda. A média aritmética das coordenadas x de ambas as interseções nos permite estimar o comprimento da mensagem desconhecida p.

Para evitar uma estimativa estatística longa dos pontos médios RM (1/2) e SM (1/2), mais algumas considerações podem ser tomadas:

1. Ponto de interseção da curva $$$R_M$ e $$$R _ {- M}$ tem a mesma coordenada x que o ponto de interseção das curvas $$$S_M$ e $$$S _ {- M}$ . Esta é essencialmente uma versão mais rigorosa de nossa hipótese estatística. (veja acima)
2. As curvas RM e SM se cruzam em m = 50%, ou $$$R_M (1/2) = S_M (1/2)$ .

Essas duas suposições fornecem uma fórmula simples para o tamanho da mensagem secreta p. Depois de escalar o eixo x para que p / 2 se torne 0 e 1 - p / 2 se torne 1, a coordenada x do ponto de interseção é a raiz da seguinte equação quadrática



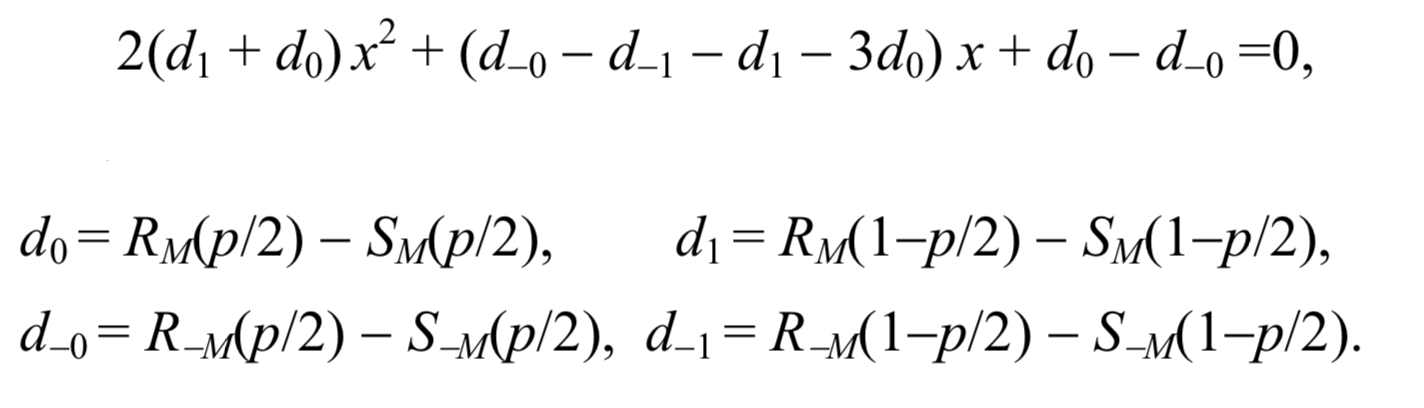
Em seguida, o comprimento da mensagem pode ser calculado pela fórmula:

$$

$$p = \ frac {x} {x- \ frac {1} {2}}$$

Aqui nosso gato entra em cena. (Não é hora de dar um nome a ele?)

Então nós temos:

• Grupos RM regulares (p / 2): 23121 un.
• Grupos SM singulares (p / 2): 14124 un.
• Grupos regulares com máscara invertida RM (p / 2): 37191 un.
• Grupos singulares com máscara invertida SM (p / 2): 8440 unid.
• Grupos regulares com LSB invertido (1-p / 2): 20298 un.
• Grupos singulares com LSB invertido SM (1-p / 2): 16206 un.
• Grupos regulares com LSB invertido e com máscara invertida RM (1-p / 2): 40603 un.
• Grupos singulares com LSB invertido e com máscara invertida SM (1-p / 2): 6947 un.

(Se você tiver muito tempo livre, poderá calculá-los, mas por enquanto sugiro que acredite nos meus cálculos)

Na agenda, deixamos uma matemática nua. Ainda se lembra de como resolver equações quadráticas?

$$

$$d_0 = 8997$$

$$

$$d _ {- 0} = $ 2875$$

$$

$$d_1 = 4092$$

$$

$$d _ {- 1} = 33656$$

Substituindo todos os d na fórmula acima, obtemos uma equação quadrática, que resolvemos como ensinado na escola.

$$

$$

$$D = (-35988) ^ 2 - 426178 * (- 19754) = $ 336361699$$

$$

$$x_1 = 1.7951 ~~~~~~~~ x_2 = -0,4204$$

Pegue uma raiz de módulo menor , ou seja, $$$x_2$ . A estimativa aproximada da mensagem incorporada no gato será a seguinte:

$$

$$p = \ frac {-0,4204} {- 0,4204 - 0,5} = 0,4567$$

Sim, este método possui uma grande vantagem e uma grande menos. A vantagem é que o método trabalha com a esteganografia comum do LSB e a esteganografia RandomLSB. Um qui-quadrado não pode se orgulhar de tal oportunidade. O método reconheceu nosso gato de aparência aleatória com precisão e estimou o tamanho da mensagem em 0,3256, o que é muito, muito preciso.

O menos está no erro grande (muito grande) desse método, que cresce junto com a mensagem longa com incorporação sequencial . Por exemplo, para um gato com 30% de ocupação, minha implementação do método fornece uma estimativa média aproximada para três canais de 0,4633 ou 46% da capacidade total, com uma ocupação de mais de 95% - 0,8597. Mas para um gato vazio, tanto quanto 0,0054. E esta é uma tendência geral que é independente da implementação. Os resultados mais precisos com o método LSB comum fornecem um comprimento de mensagem interno de 10% + - 5%.

Mais ou menos

Para não ser pego, é preciso ser inesperado e usar ± 1 de codificação. Em vez de alterar o bit menos significativo no byte colorido, aumentaremos ou diminuiremos o byte inteiro em um. Existem apenas duas exceções:

• não podemos reduzir zero, portanto vamos aumentá-lo,
  
• também não podemos aumentar 255; portanto, sempre diminuiremos esse valor.
  

Para todos os outros valores de bytes, selecionamos completamente aleatoriamente um aumento de um ou um decréscimo. No topo dessa manipulação, o LSB mudará como antes. Para maior confiabilidade, é melhor usar bytes aleatórios para gravar uma mensagem.

Aqui está o nosso amigo gato:



Externamente, a introdução é imperceptivelmente exatamente pela mesma razão pela qual as diferenças entre (0, 0, 0) e (1, 1, 1) não eram visíveis.



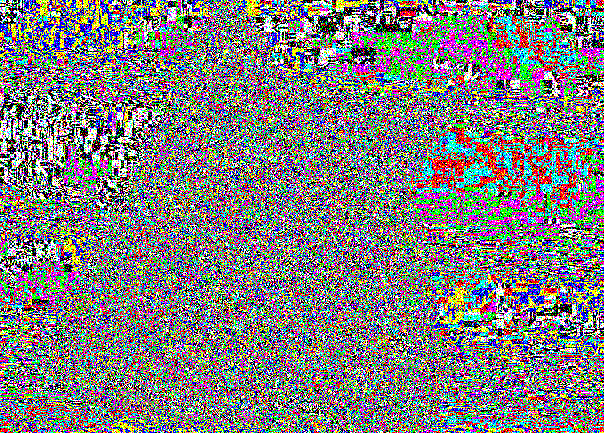
A fatia LSB permanece simplesmente barulhenta devido à gravação em locais aleatórios.



O qui-quadrado ainda é cego, e o método RS fornece uma estimativa aproximada de 0,0036 .

Para não ficar muito feliz, leia este artigo aqui.

Os mais atentos podem perguntar como podemos receber uma mensagem se bytes inteiros forem alterados aleatoriamente, e não temos uma senha para definir o PRNG (é melhor usar sementes diferentes, o estado do gerador ou senhas, para trabalhar com a codificação RandomLSB e ± 1). A resposta é o mais simples possível. Recebemos a mensagem da mesma maneira que fizemos sem a codificação ± 1. Podemos nem saber sobre o seu uso. Repito, usamos esse truque apenas para ignorar as ferramentas de detecção automática . Ao incorporar / recuperar uma mensagem, trabalhamos apenas com o LSB e nada mais. No entanto, ao detectar, precisamos levar em consideração o contexto de implementação, ou seja, todos os bytes da imagem, para criar estimativas estatísticas. Este é precisamente todo o sucesso de ± 1 codificação.

Em vez de uma conclusão

Outra tentativa muito boa de usar estatísticas contra a esteganografia LSB foi feita em um método chamado Sample Pairs. Você pode encontrá-lo aqui. Sua presença aqui tornaria o artigo muito acadêmico, por isso deixo-o interessado em leitura extracurricular. Mas, antecipando as perguntas do público, responderei imediatamente: não, ele não entende ± 1 código.

E, claro, aprendizado de máquina. Métodos modernos baseados em ML dão resultados muito bons. Você pode ler sobre isso aqui e aqui .

Com base neste artigo, uma pequena ferramenta foi escrita (por enquanto). Ele pode gerar dados, realizar um ataque visual separadamente nos canais, calcular a avaliação RS, SPA e visualizar os resultados do qui-quadrado. E ela não vai parar por aí.

Para resumir, quero dar algumas dicas:

• Incorpore a mensagem em bytes aleatórios.
• Reduza a quantidade de informações incorporadas o máximo possível (lembre-se do tio Hamming).
• Use ± 1 codificação.
• Escolha fotos com LSB barulhento.
• UPD de Remdalp : use imagens que não aparecem em lugar nenhum.
• Seja legal!

Ficarei feliz em ver suas sugestões, acréscimos, correções e outros comentários!

PS: Quero expressar um agradecimento especial ao PavelMSTU pelas consultas e chutes motivacionais.