Uma introdução simples à ALU para redes neurais: explicação, significado físico e implementação

Recentemente, pesquisadores do Google DeepMind, incluindo um conhecido cientista de inteligência artificial, autor do livro " Understanding Deep Learning ", Andrew Trask, publicaram um artigo impressionante que descreve um modelo de rede neural para extrapolar os valores de funções numéricas simples e complexas com alto grau de precisão.

Neste post, explicarei a arquitetura do NALU ( dispositivos lógicos aritméticos neurais, NALU), seus componentes e diferenças significativas em relação às redes neurais tradicionais. O principal objetivo deste artigo é explicar de maneira simples e intuitiva o NALU (implementação e idéia) para cientistas, programadores e estudantes que são novos nas redes neurais e no aprendizado profundo.

Nota do autor : Também recomendo a leitura do artigo original para um estudo mais detalhado do tópico.

Quando as redes neurais estão erradas?

Imagem retirada deste artigo.

Em teoria, as redes neurais devem aproximar bem as funções. Eles quase sempre conseguem identificar correspondências significativas entre dados de entrada (fatores ou recursos) e resultados (rótulos ou destinos). É por isso que as redes neurais são usadas em muitos campos, desde o reconhecimento de objetos e sua classificação até a tradução de fala em texto e a implementação de algoritmos de jogos que podem vencer os campeões mundiais. Muitos modelos diferentes já foram criados: redes neurais convolucionais e recorrentes, autocoders etc. O sucesso na criação de novos modelos de redes neurais e aprendizado profundo é um grande tópico em si.

No entanto, de acordo com os autores do artigo, as redes neurais nem sempre lidam com tarefas que parecem óbvias para as pessoas e até para as abelhas ! Por exemplo, é uma conta oral ou operações com números, bem como a capacidade de identificar dependência de relacionamentos. O artigo mostrou que os modelos padrão de redes neurais não conseguem lidar com o mapeamento idêntico (uma função que traduz um argumento em si mesmo, $$$f (x) = x$) É a relação numérica mais óbvia. A figura abaixo mostra o MSE de vários modelos de redes neurais ao aprender sobre os valores dessa função.


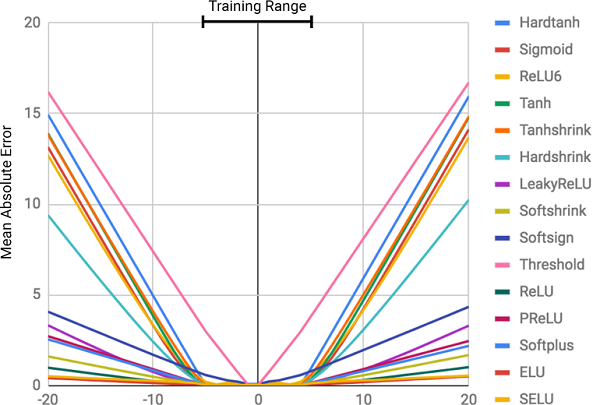A figura mostra o erro quadrático médio para redes neurais padrão usando a mesma arquitetura e diferentes funções de ativação (não lineares) nas camadas internas

Por que as redes neurais estão erradas?

Como pode ser visto na figura, a principal razão para as falhas é a não linearidade das funções de ativação nas camadas internas da rede neural. Essa abordagem funciona muito bem para determinar relacionamentos não lineares entre dados de entrada e respostas, mas é terrivelmente errado ir além dos dados sobre os quais a rede aprendeu. Assim, as redes neurais fazem um excelente trabalho de lembrar uma dependência numérica dos dados de treinamento, mas não podem extrapolá-las.

É como colocar uma resposta ou um tópico antes de um exame sem entender o assunto. É fácil passar no teste se as perguntas forem semelhantes às tarefas de casa, mas se for o entendimento do assunto que está sendo testado e não a capacidade de lembrar, fracassaremos.


Isso não estava no programa do curso!

O grau de erro está diretamente relacionado ao nível de não linearidade da função de ativação selecionada. O diagrama anterior mostra claramente que funções não lineares com restrições rígidas, como uma tangente sigmóide ou hiperbólica ( Tanh ), podem lidar com a tarefa de generalizar as dependências muito piores que as funções com restrições moles, como uma transformação linear truncada ( ELU , PReLU ).

Solução: Bateria Neural (NAC)

Uma bateria neural ( NAC ) está no coração do modelo NALU . Essa é uma parte simples, porém eficaz, de uma rede neural que lida com adição e subtração , necessária para o cálculo eficiente de relações lineares.

O NAC é uma camada linear especial de uma rede neural, cujo peso é imposto a uma condição simples: eles podem assumir apenas 3 valores - 1, 0 ou -1 . Essas restrições não permitem que a bateria altere o intervalo de dados de entrada e permanece constante em todas as camadas da rede, independentemente do número e das conexões. Assim, a saída é uma combinação linear dos valores do vetor de entrada, que pode ser facilmente uma operação de adição e subtração.

Pensamentos em voz alta : para uma melhor compreensão dessa afirmação, vejamos um exemplo de construção de camadas de uma rede neural que executa operações aritméticas lineares nos dados de entrada.


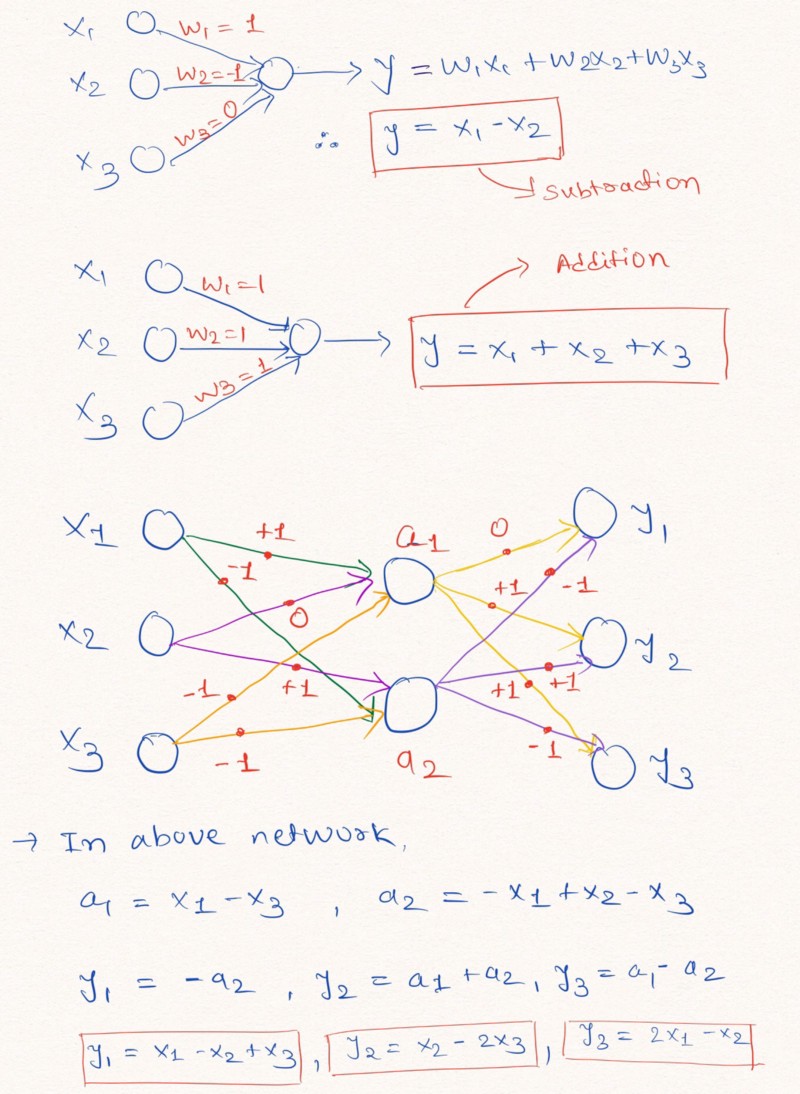A figura ilustra como as camadas de uma rede neural sem adicionar uma constante e com possíveis valores de pesos -1, 0 ou 1, podem executar extrapolação linear

Como mostrado acima na imagem das camadas, a rede neural pode aprender a extrapolar os valores de funções aritméticas simples como adição e subtração ( $$$y = x_1 + x_2$e $$$y = x_1 - x_2$), usando as restrições dos pesos com valores possíveis de 1, 0 e -1.

Nota: a camada NAC, neste caso, não contém um termo livre (constante) e não aplica transformações não lineares aos dados.

Como as redes neurais padrão não conseguem lidar com a solução do problema sob restrições semelhantes, os autores do artigo oferecem uma fórmula muito útil para calcular esses parâmetros por meio de parâmetros clássicos (ilimitados) $$$\ hat {W}$e $$$\ hat {M}$. Dados de peso, como todos os parâmetros das redes neurais, podem ser inicializados e selecionados aleatoriamente no processo de treinamento da rede. Fórmula para calcular o vetor $$$W$através de $$$\ hat {W}$e $$$\ hat {M}$é assim:

$$

$$W = tanh (\ hat {W}) \ odot \ sigma (\ hat {M})$$

A fórmula usa o produto da matriz elementar

O uso desta fórmula garante a faixa limitada de valores W pelo intervalo [-1, 1], que é mais próximo do conjunto -1, 0, 1. Além disso, as funções dessa equação são diferenciáveis por parâmetros de peso. Assim, será mais fácil para nossa camada NAC aprender valores $$$W$usando descida de gradiente e propagação de erro de volta . A seguir, é apresentado um diagrama da arquitetura da camada NAC .


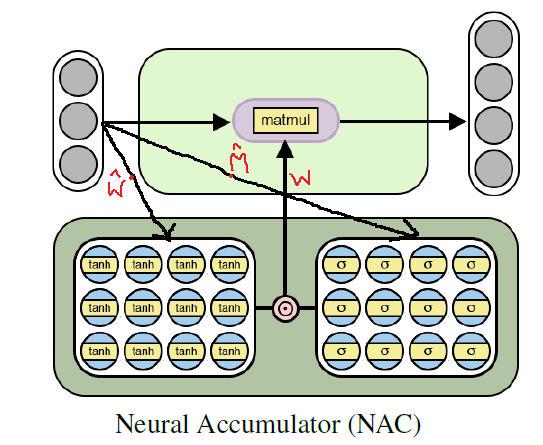A arquitetura de uma bateria neural para treinamento em funções aritméticas elementares (lineares)

Implementação Python NAC usando Tensorflow

Como já entendemos, o NAC é uma rede neural bastante simples (camada de rede) com pequenos recursos. A seguir, é apresentada uma implementação de uma única camada NAC em Python, usando as bibliotecas Tensoflow e NumPy.


No código acima $$$\ hat {W}$e $$$\ hat {M}$são inicializados usando distribuição uniforme, mas você pode usar qualquer método recomendado para gerar uma aproximação inicial para esses parâmetros. Você pode ver a versão completa do código no meu repositório GitHub (o link é duplicado no final da postagem).

Seguindo em frente: da adição e subtração ao NAC para expressões aritméticas complexas

Embora o modelo de uma rede neural simples descrita acima lide com as operações mais simples, como adição e subtração, precisamos ser capazes de aprender com os muitos significados de funções mais complexas, como multiplicação, divisão e exponenciação.

Abaixo está a arquitetura NAC modificada, que é adaptada para a seleção de operações aritméticas mais complexas através do logaritmo e levando o expoente dentro do modelo. Observe as diferenças entre esta implementação do NAC e a já discutida acima.


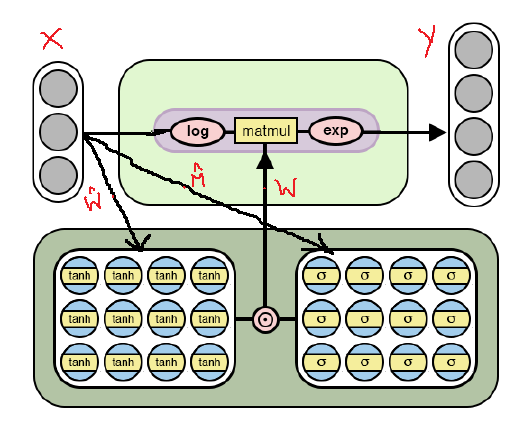Arquitetura NAC para operações aritméticas mais complexas

Como pode ser visto na figura, logaritmos os dados de entrada antes de multiplicar pela matriz de pesos e, em seguida, calculamos o expoente do resultado. A fórmula para os cálculos é a seguinte:

$$

$$Y = exp (W \ marcador (log (| x | + \ epsilon)))$$

A fórmula de saída para a segunda versão do NAC . $$$\ epsilon$aqui está um número muito pequeno para evitar situações como log (0) durante o treinamento

Assim, para ambos os modelos NAC , o princípio de operação, incluindo o cálculo da matriz de pesos com restrições $$$W$através de $$$\ hat {W}$e $$$\ hat {M}$não muda A única diferença é o uso de operações logarítmicas na entrada e saída no segundo caso.

Segunda versão do NAC em Python usando Tensorflow

O código, como a arquitetura, dificilmente mudará, exceto pelas melhorias indicadas no cálculo do tensor dos valores de saída.



Lembro novamente que a versão completa do código pode ser encontrada no meu repositório GitHub (o link é duplicado no final do post).

Juntando tudo: uma unidade lógica aritmética neural (NALU)

Como muitos já imaginaram, podemos aprender com praticamente qualquer operação aritmética, combinando os dois modelos discutidos acima. Essa é a idéia principal do NALU , que inclui uma combinação ponderada de NAC elementar e complexo, controlada por um sinal de treinamento. Assim, os NACs são os elementos básicos para a criação de NALUs e, se você entender o design deles, será fácil construir NALUs . Se você ainda tiver dúvidas, tente ler as explicações para os dois modelos NAC novamente. Abaixo está um diagrama com a arquitetura NALU .


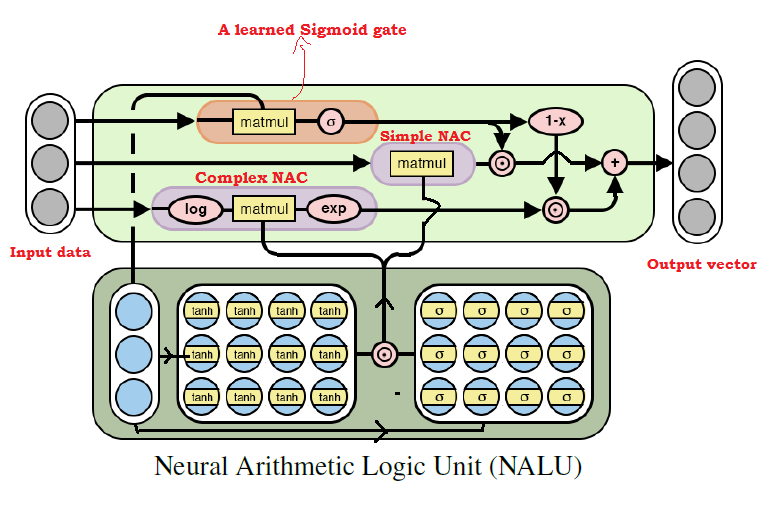Diagrama da arquitetura NALU com explicações

Como pode ser visto na figura acima, as duas unidades NAC (blocos roxos) dentro da NALU são interpoladas (combinadas) através do sinal de treinamento sigmoide (bloco laranja). Isso permite que você desative a saída de qualquer um deles, dependendo da função aritmética, cujos valores estamos tentando encontrar.

Como mencionado acima, a unidade elementar do NAC é uma função acumulativa, que permite ao NALU executar operações lineares elementares (adição e subtração), enquanto a unidade complexa do NAC é responsável pela multiplicação, divisão e exponenciação. A saída em NALU pode ser representada como uma fórmula:


A partir da fórmula NALU acima, podemos concluir que, com $$$g = 0$a rede neural selecionará apenas valores para operações aritméticas complexas, mas não para operações elementares; e vice-versa - no caso de $$$g = 1$. Assim, em geral, o NALU é capaz de aprender qualquer operação aritmética que consiste em adição, subtração, multiplicação, divisão e aumento de potência e extrapolar com sucesso o resultado além dos limites dos intervalos dos valores dos dados de origem.

Implementação Python NALU usando Tensorflow

Na implementação do NALU, usaremos o NAC elementar e complexo, que já definimos.


Mais uma vez, observo que, no código acima, inicializei novamente a matriz de parâmetros $$$G$usando distribuição uniforme, mas você pode usar qualquer maneira recomendada para gerar uma aproximação inicial.

---

Sumário

Para mim, pessoalmente, a ideia de NALU é uma grande inovação no campo da IA, especialmente em redes neurais, e parece promissora. Essa abordagem pode abrir as portas para as áreas de aplicação em que as redes neurais padrão não conseguem lidar.

Os autores do artigo falam sobre várias experiências usando o NALU : da seleção dos valores das funções aritméticas elementares à contagem do número de dígitos manuscritos em uma determinada série de imagens MNIST , o que permite às redes neurais verificar programas de computador!

Os resultados causam uma impressão impressionante e provam que o NALU lida com quase todas as tarefas relacionadas à representação numérica, melhores do que os modelos padrão de redes neurais. Encorajo os leitores a se familiarizarem com os resultados das experiências, a fim de entender melhor como e onde o modelo NALU pode ser útil.

No entanto, deve-se lembrar que nem o NAC nem o NALU são a solução ideal para qualquer tarefa. Em vez disso, eles representam a ideia geral de como criar modelos para uma classe específica de operações aritméticas.

---

Abaixo está um link para meu repositório GitHub, que contém a implementação completa do código do artigo.
github.com/faizan2786/nalu_implementation

Você pode verificar independentemente a operação do meu modelo em várias funções selecionando hiperparâmetros para uma rede neural. Faça perguntas e compartilhe suas opiniões nos comentários deste post, e farei o possível para responder.

PS (do autor): este é o meu primeiro post escrito, por isso, se você tiver dicas, sugestões e recomendações para o futuro (técnico e geral), escreva para mim.

PPS (do tradutor): se você tiver comentários sobre a tradução ou o texto, escreva-me uma mensagem pessoal. Estou especialmente interessado na redação do sinal de gate aprendido - não tenho certeza de que poderia traduzir esse termo com precisão.