Determinação do número de andares de uma casa a partir de sua fotografia sem aprendizado de máquina

Neste artigo, darei, em minha opinião, uma solução interessante para o problema do reconhecimento por computador de objetos em uma imagem sem o uso de treinamento.

Tarefa: tirando uma foto de um prédio de vários andares, tente determinar o número de andares nele.

Uma boa estimativa para o número de andares pode fornecer o número de janelas na vertical da casa. Janelas, varandas e outros objetos são boas características de pisos (principalmente em edifícios residenciais). Considerarei prédios residenciais, cujas imagens são fáceis de encontrar na rede. Uma limitação importante deve ser observada com antecedência: a casa na imagem deve ser mostrada completamente na vertical, para que seja possível detectar visualmente todos os pisos.

A tarefa é racionalmente dividida em duas etapas:

1. Procure a “faixa” vertical das janelas a serem contadas. Duas subtarefas: em primeiro lugar, é necessário procurar janelas na área de imagem ocupada pela casa e, em segundo lugar, há muitas janelas em edifícios residenciais, não faz sentido analisá-las todas. É necessário destacar entre eles a sequência vertical mais adequada para análises subsequentes.
2. Determinação do número de pisos (janelas ou outros objetos característicos) pela área selecionada da casa.

Este artigo é dedicado principalmente à primeira etapa da solução. O segundo passo ainda está em desenvolvimento, mas também darei alguns resultados de sua solução.

Etapa 1. Pesquise a área com janelas

A idéia principal é que uma série de objetos idênticos (como janelas) que sejam bem distinguíveis em uma casa em uma fileira de objetos idênticos crie uma sequência periódica de brilho de pixel. Esta é precisamente a sequência a ser encontrada. Abaixo estão os principais estágios do algoritmo.

Primeiro, traduzimos a imagem em tons de cinza e a escalamos (usei as figuras 400x600px)

Fig. 1 Imagem preto e branco original

Mais adiante no loop:

1. Seleção na imagem de uma faixa relativamente estreita (40px) em toda a altura (Fig. 2, imagem inferior sem pontos)
2. Média de brilho ao longo da largura da faixa. Acontece a linha w da distribuição do brilho médio sobre a altura da casa (Fig. 2 gráfico superior). Possui uma estrutura periódica claramente visível, característica da área onde há janelas. Janelas localizadas na sombra são menos distinguíveis, mas isso não fará mal.
3. A diferença dw dos valores de w e w deslocados pela distância sh é calculada. O método de busca usa esse valor de deslocamento sh para obter a redução máxima na mediana das diferenças dw (Fig. 2, gráfico inferior).
   
   
   Fig.2 "Faixa" das janelas

No entanto, não basta encontrar a faixa da imagem na qual a mediana foi mais fortemente reduzida. O fato é que áreas com vegetação ou céu, com pequenos valores de cisalhamento, podem causar uma diminuição maior que as janelas. Mas se traçarmos a dependência do valor mediano do valor de deslocamento para tiras com e sem janelas, podemos notar uma diferença importante: com valores de deslocamento próximos à altura dos pisos, o gráfico com janelas tem extremos claramente visíveis. Assim, não é necessário medir o nível atingível absoluto da mediana, mas sua diminuição máxima em relação ao máximo no processo de aumento do turno para cada janela. Este é um ponto chave.

sem janelas	com janelas

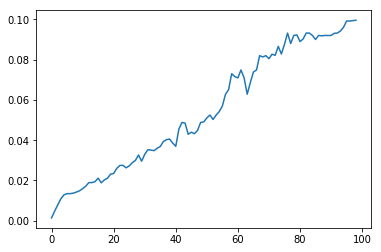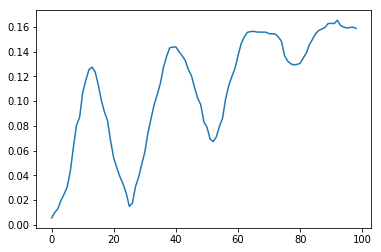Fig. 3 Alteração da mediana do brilho médio com o aumento da mudança

Abaixo está o código python3 com comentários.

image = Image.open("raf_data/32.jpg").resize((600,400)) # . img = np.array(image.convert("L"), dtype=float)/255 SEARCH_WIDTH = 40 #    x_opt = [0, 1] #    :      sh_range = range(1,100) #    kmax = 0 #       for x in range(0, img.shape[1]-SEARCH_WIDTH, int(SEARCH_WIDTH/2)): amax = 0 amin = 1 #      for sh in sh_range: #    w = img[:,x:x+SEARCH_WIDTH].mean(axis=1) aim = (pd.DataFrame(w)-pd.DataFrame(w).shift(sh))[sh:].abs().median().values[0] #    aim    sh if aim>amax: amax = aim amin = amax if aim<amin: amin = aim aim_k = amax/amin if aim_k>kmax: x_opt = [x, sh, w] kmax = aim_k print(' : {0},  : {1}'.format(x_opt[0], x_opt[1])) 

A Fig. 2 marca os pontos definidos à distância do turno encontrado. Como você pode ver, eles marcam bem todas as janelas. I.e. já sabemos a altura do chão!
O algoritmo considerado encontra boas zonas regulares nas fachadas de vários edifícios residenciais (Fig. 4).



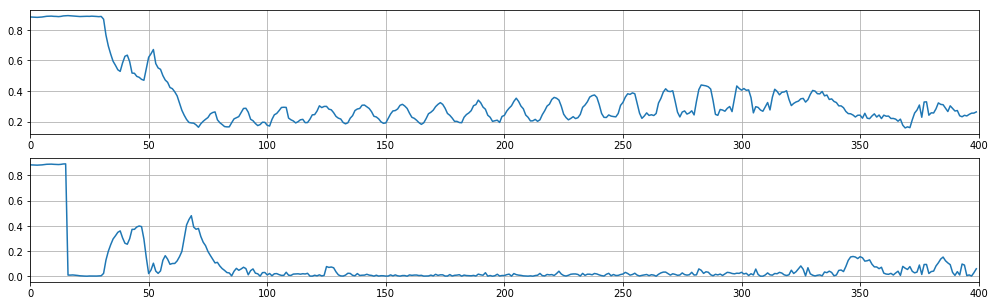
Fig. 4 Exemplo

Etapa 2. Contando o número de andares

Nesta etapa, as principais dificuldades começam. Outras ações podem ser as seguintes:

1. Estime a altura da casa analisando a curva das diferenças de brilho médio ou usando o aprendizado de máquina). Divida a altura da casa pela altura do piso e obtenha o número de andares.
2. Na janela encontrada na primeira etapa, procure objetos semelhantes a janelas e conte-os diretamente, por exemplo, em pontos específicos.

Parece natural tentar primeiro o primeiro método: uma vez conhecida a altura dos pisos, resta determinar a altura da casa. No entanto, esquemas semelhantes aos mostrados na etapa 1 são pouco adequados para determinar a altura da casa, levando em consideração todos os limites e transições possíveis. Em alguns casos, é possível obter bons exemplos de trabalho, mas para um resultado consistentemente bom, são necessárias abordagens usando o aprendizado de máquina.

Fig. 5 Determinando a altura da casa usando uma floresta aleatória