Um dos elementos mais high-tech das indústrias aeroespaciais e militares modernas são os sistemas de navegação inercial de alta precisão (RNAs). A tarefa de tais sistemas, com base em acelerômetros e giroscópios ópticos, é determinar as velocidades angulares, acelerações de um objeto em movimento e a orientação geral do objeto no espaço tridimensional.

As especificidades da modelagem de RNA são que, no campo da modelagem, ocorrem frequentemente movimentos retilíneos e rotacionais, o que afeta fortemente a operação desses sistemas e, portanto, exige consideração. Em nosso artigo, falaremos brevemente sobre o que é o efeito Sagnac e como os dispositivos baseados nele podem ser numericamente investigados no pacote COMSOL Multiphysics ^® .

Para uma navegação conveniente, apresentamos no início um breve resumo do artigo:

1. O que são giroscópios ópticos
2. As especificidades da contabilização da rotação na simulação
3. Efeito Sagnac: base teórica
4. Modelo de interferômetro Sagnac no COMSOL Multiphysics ^®
5. Conclusão

Giroscópios ópticos e o efeito Sagnac

Talvez seja o interferômetro clássico Sagnac que melhor demonstre a necessidade de registro de alta precisão do movimento não inercial do domínio da simulação.

O interferômetro Sagnac mais simples consiste nos seguintes componentes:

• Fonte de luz
• Um divisor de feixe que direciona a luz de uma fonte por dois caminhos diferentes e os combina
• Um conjunto de espelhos (geralmente incluindo dois ou três espelhos)

O divisor de feixe e os espelhos formam uma trajetória triangular ou retangular ao longo da qual a luz se propaga nas duas direções. Nesse momento, o próprio sistema de navegação (assim como a aeronave ou espaçonave em que está instalado) também gira a uma certa velocidade angular. Observando a interferência dos raios de luz (devido ao efeito Sagnac) que se propagam ao longo dessas trajetórias, é possível determinar a velocidade angular do sistema com uma precisão muito alta.

A medição de pequenas rotações é vital para determinar e controlar a orientação dos objetos nas modernas indústrias de defesa e espaço. Atualmente, o laser anelar e os giroscópios de fibra óptica, cujo princípio também se baseia no efeito Sagnac, são os mais amplamente utilizados. Observe que um giroscópio a laser de anel é altamente preciso, barato e fácil de manter, porque, diferentemente dos giroscópios mecânicos, ele não contém peças rotativas.

Modelando a propagação da luz em componentes ópticos rotativos

Como calcular o caminho da propagação da luz em um sistema rotativo de espelhos, prismas e divisores de feixe? Para não se aprofundar na teoria da relatividade, suponha que a velocidade de rotação seja muito menor que a velocidade da luz, mas seja grande o suficiente para que tenhamos em conta a rotação. Há pelo menos duas abordagens para resolver esse problema:

1. Reescreva equações para a propagação da luz em um referencial não inercial
2. Gire a estrutura em tempo real ao propagar raios

A diferença entre essas abordagens é que, em um caso, o modelo está em um quadro de referência não inercial conectado a um interferômetro móvel (opção nº 1) ou em um sistema de referência “laboratorial” fixo no espaço (opção nº 2). Como a segunda opção é muito mais simples de implementar, usaremos essa abordagem para simular o interferômetro Sagnac.

O pacote COMSOL Multiphysics ^® é bastante eficaz para modelar dispositivos com uma estrutura móvel ou deformada (que inclui o interferômetro Sagnac e um giroscópio a laser de anel) e permite integrar e simular vários processos físicos interdisciplinares em um único modelo computacional.

A análise de estruturas deformáveis ​​e móveis é tradicionalmente realizada com cuidado especial, uma vez que é usada em vários campos: na análise de estresse térmico, na interação de um fluido com uma estrutura, em fluxos multifásicos, bem como em galvanoplastia, dispositivos piezoelétricos e assim por diante. De fato, para o rastreamento preciso de raios em uma estrutura móvel, basta indicar a velocidade angular do sistema e iniciar um cálculo padrão com base nas tecnologias de óptica geométrica .

Efeito Sagnac: base teórica

Antes de prosseguir com a descrição do modelo implementado no pacote, vamos examinar brevemente qual é o efeito Sagnac.

Imagine que a luz viaja estritamente em torno de um círculo (por exemplo, ao longo de um cabo de fibra óptica) em duas direções opostas, como ilustrado na Fig. 1. Ponto de disparo do feixe - $$$P_0$. A linha tracejada indica a direção no sentido horário e a linha sólida grossa indica a direção no sentido anti-horário. Os raios de luz nessa configuração serão contrários entre si, pois se propagam pela circunferência em direções opostas.

Se o anel estivesse imóvel, os caminhos dos raios se cruzariam duas vezes: primeiro no ponto oposto do círculo e depois no ponto inicial $$$P_0$. Agora imagine que o anel gira no sentido anti-horário em torno de seu centro com uma certa velocidade angular. Se seguirmos o movimento do ponto $$$P_0$durante a propagação da luz, veremos que um raio que se propaga no sentido horário retornará a ele quando já estiver em uma nova posição, $$$P_1$. Quando ao ponto $$$P_0$um raio propagando no sentido anti-horário retornará, ele se moverá mais e estará em posição $$$P_2$. $$$P_2$localizado a uma distância maior $$$P_0$que $$$P_1$porque o círculo também gira no sentido anti-horário.

Fig. 1. Propagação da luz no sentido horário e anti-horário ao longo da borda de um círculo rotativo.

Obviamente, a ilustração na Fig. 1 é significativamente dimensionada para maior clareza e, na realidade, a distância entre os pontos é 10 bilhões de vezes menor. No entanto, mesmo neste caso, a diferença no caminho óptico percorrido leva a uma mudança de fase e, consequentemente, a interferências.

Sem se aprofundar nos cálculos teóricos (mas se forem interessantes, recomendamos o seguinte trabalho clássico de Post, Evert J. “Efeito Sagnac”, Reviews of Modern Physics, 39, nº 2, p. 475, 1967 ), a relação final entre a velocidade angular $$$\ Omega$e a diferença no caminho óptico $$$\ Delta L$pode ser expresso como:

$$

$$\ Delta L = {{4 \ Omega A} \ sobre {c_0}}$$

Onde $$$A$A área do círculo está sendo considerada e $$$c_0$É a velocidade da luz.

Em geral, o efeito Sagnac é ainda mais geral do que o exemplo descrito acima. O caminho de propagação de dois raios que se aproximam pode ter qualquer forma, mas o atraso entre eles sempre será proporcional ao tamanho da região, limitado pelo contorno no qual os raios se propagam. Além disso, esse efeito também é observado nos casos em que o centro de rotação não coincide com o centro do contorno.

Modelo de teste do interferômetro Sagnac baseado no traçado de raios ópticos

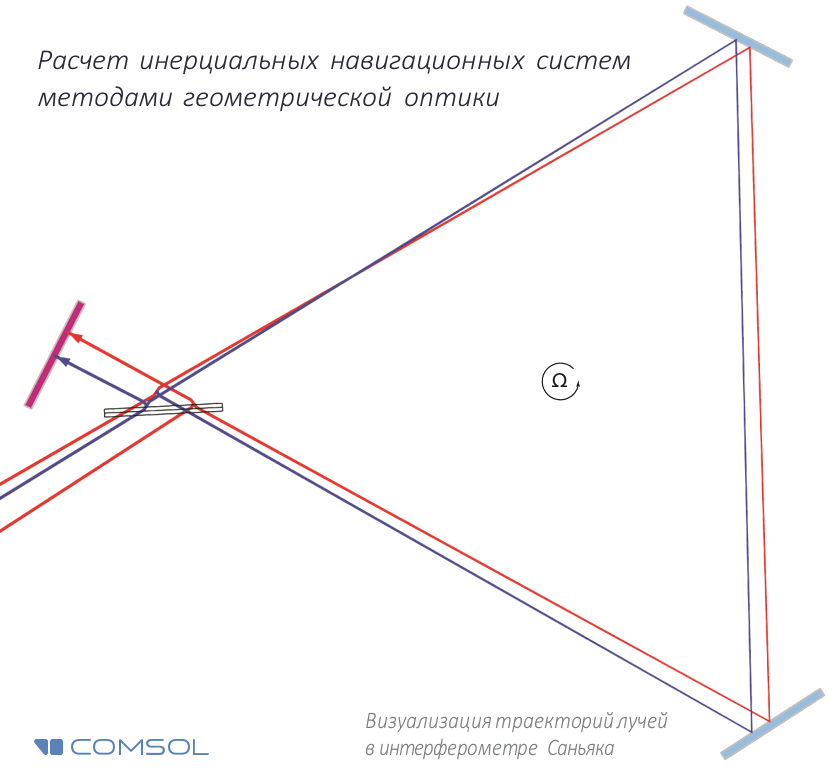
Para verificar como o COMSOL Multiphysics ^® será calculado $$$\ Delta L$e, portanto, a sensibilidade do dispositivo, consideramos o design de teste do interferômetro Sagnac, no qual a luz não se propaga em torno da circunferência, mas ao longo do perímetro do triângulo, no topo dos quais existem dois espelhos e um divisor de feixe (Fig. 2).

Fig. 2. Esquema do interferômetro Sagnac.

O feixe inicial passa através de um divisor de feixes, como resultado dos quais dois raios da mesma intensidade são formados. No momento da saída do divisor de feixe, eles estão no mesmo ponto e têm a mesma fase. Como o sistema de espelhos gira, quando os raios retornam ao divisor de feixes, seus caminhos ópticos (e, portanto, fases) são diferentes um do outro.

Na prática, em vez de pequenas quantidades $$$\ Delta L$os sistemas frequentemente detectam uma mudança de frequência (ou frequência de batida) $$$\ Delta \ nu$:

$$

$${{\ \ Delta \ nu} \ over {\ nu}} = {{\ Delta L} \ sobre {L}}$$

Aqui $$$L$O comprimento efetivo do contorno ao longo do qual os raios se propagam e $$$\ nu$- a frequência deles. Por favor note que $$$\ Delta L$determinado diretamente no cálculo.

O processo de rastreamento numérico de raios pode ser facilmente automatizado, por exemplo, para realizar análises paramétricas. Na fig. A Figura 3 mostra os resultados da análise paramétrica em uma ampla faixa de valores de velocidade angular, de relativamente pequeno a muito grande.

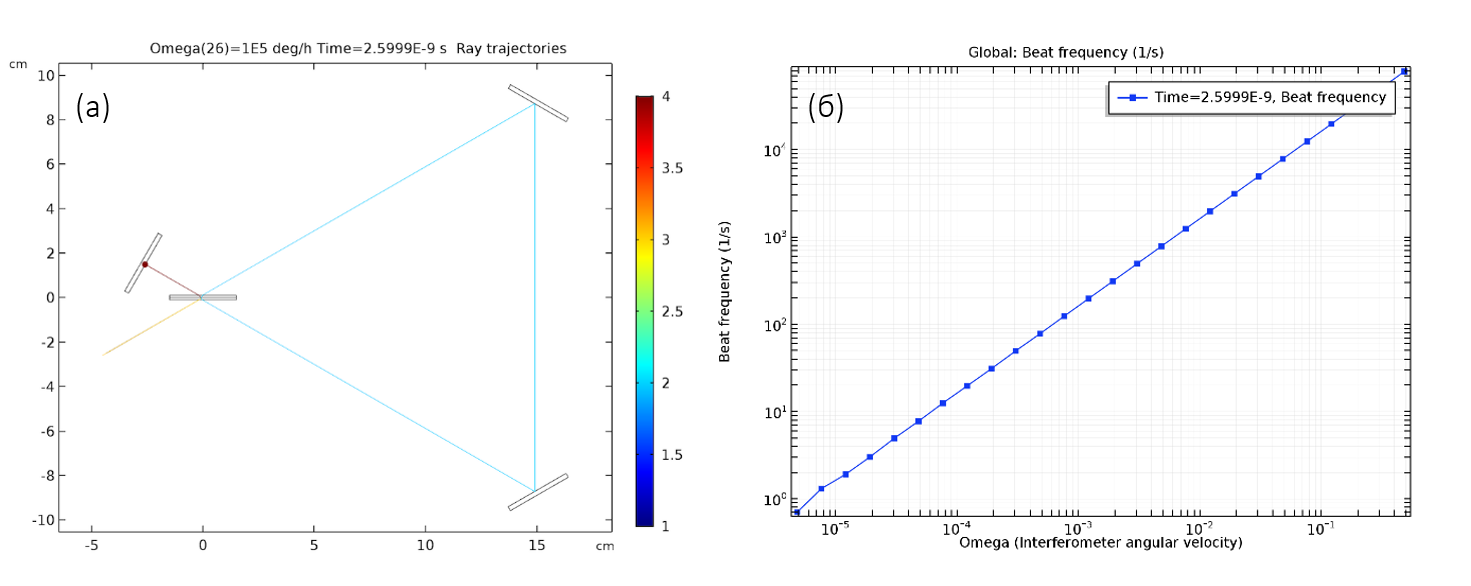
Fig. 3. (a) Trajetos de raios em um interferômetro de teste. As discrepâncias na trajetória dos dois raios são tão insignificantes que não são visíveis nem em close-up (b) A dependência da frequência de batimento na frequência angular de rotação do sistema.

A frequência de batida correspondente está em excelente concordância com os valores teóricos. Alterando a distância entre os espelhos, pode-se demonstrar que a inclinação dessa linha é proporcional à área da região triangular entre os raios que se aproximam.

Um olhar para o futuro ou a aplicação prática da modelagem numérica de giroscópios ópticos

Os resultados acima demonstram que, rastreando raios em uma geometria rotativa (quadro) usando a técnica descrita, é possível calcular com alta precisão a sensibilidade dos dispositivos com base no efeito Sagnac, se a velocidade de rotação for baixa em comparação com a velocidade da luz (ou seja, sem efeitos relativísticos). Assim, graças a esse novo modelo , especialistas em modelagem e engenheiros que trabalham com sistemas de orientação angular agora terão um modelo de trabalho pronto para estudar o efeito Sagnac, subjacente à operação de giroscópios a laser em anel.

Um leitor atento provavelmente perguntará sobre a necessidade de uma simulação numérica, dado o fato de que o efeito Sagnac é descrito com precisão pela fórmula acima. Vale a pena considerar que as RNAs reais são muito mais complicadas do que a configuração mais simples com um divisor de feixe e dois espelhos, discutidos acima. Tais sistemas são instalados em conjunto com outros dispositivos sensíveis em um espaço limitado; é necessária uma estrutura adicional, o que garante a imobilidade dos componentes ópticos entre si. Além disso, muitas vezes as RNAs trabalham em ambientes agressivos e são afetadas por estresse mecânico, temperatura e campos eletromagnéticos. Esses fatores afetam o comportamento e a sensibilidade do giroscópio, o que requer uma consideração mais detalhada e completa e não pode ser descrito pela mesma fórmula simples.

Assim, o traçado de raios apresentado em um interferômetro Sagnac ou em um giroscópio a laser de anel será apenas o primeiro passo em uma análise multifísica complexa e de alta precisão de grandes sistemas ópticos. O COMSOL Multiphysics ^® permite o traçado de raios nas condições mais realistas, levando em consideração o aquecimento e as deformações térmicas dos componentes ópticos, o que abrirá novas possibilidades para uma melhor compreensão e avaliação da sensibilidade e precisão de sistemas de navegação inercial complexos.

Informações Adicionais

Este material é baseado nos seguintes artigos:

• C. Boucher. Entendendo o efeito Sagnac através da simulação de óptica de raios , Laser Focus World, agosto de 2018
• Simulação de um interferômetro Sagnac e um giroscópio a laser de anel usando métodos de óptica geométrica , blog corporativo COMSOL

Para um conhecimento mais detalhado dos métodos e exemplos descritos, você pode solicitar uma versão demo gratuita e totalmente funcional do COMSOL Multiphysics ^® nos comentários ou através do link .

Também convidamos todos em 1º de novembro para o evento principal para usuários atuais e futuros do COMSOL - COMSOL Day em Moscou .