Aprovou um compromisso - você pode se casar!

1. Introdução

O método dos elementos finitos (FEM ou FEM, eles têm no exterior) firmemente entrou na prática de cálculos de engenharia no projeto de sistemas complexos. Em grande parte, isso se refere a cálculos de força da mecânica. A aplicação desse método, implementada pelo software apropriado, reduz significativamente o ciclo de desenvolvimento do dispositivo final, eliminando a massa de verificações experimentais necessárias ao usar cálculos clássicos com base nos métodos de sopromat e mecânica estrutural. Até o momento, muitos aplicativos foram desenvolvidos para implementar o FEM. Na vanguarda está o poderoso ANSYS, nas laterais e a uma distância honorária - sistemas CAD com um módulo FEM integrado (SolidWorks, Siemens NX, Creo Parametric, Compass 3D).

O CalculiX é forte, mas difícil e incompreensível. Vamos consertar isso?



Naturalmente, o MEF penetrou no campo da educação - para usá-lo em tarefas reais, é necessário o treinamento de especialistas relevantes. Nas capitais, nas grandes universidades técnicas, a situação nessa área é mais ou menos normal e, em nossa região, o mesmo ANSYS é usado, por exemplo, no Departamento de Teoria da Elasticidade da Universidade Federal do Sul. Mas na periferia, em universidades estreitamente especializadas e não ricas, a situação é deplorável. E é simples - o ANSYS custa cerca de 2 milhões de rublos para um local de trabalho e é necessário mais de um local. Infelizmente, nem todas as universidades podem pagar entre 30 e 40 milhões para organizar uma aula de informática para ensinar o uso do MEF.

Uma das alternativas é o uso de software livre no processo educacional. Felizmente, esse software está disponível. No entanto, praticamente não existem materiais em língua russa em seu uso. Corrigindo esta situação, vou dedicar este artigo à introdução do CalculiX - um pacote de software livre aberto projetado para resolver problemas tridimensionais lineares e não lineares da mecânica de um corpo deformável sólido e mecânica de fluidos e gases usando o método dos elementos finitos.

1. O que é o CalculiX e onde obtê-lo. Instalação do Windows

O pacote CalculiX é um conjunto de utilitários de console, incluindo um pré-processador para preparar dados de origem, um solucionador FEM e um pós-processador para processar os resultados. O CalculiX é usado de forma independente e como parte de outros produtos, entre os quais o FreeCAD está ganhando impulso. Outra questão é que o CalculiX ainda é pouco conhecido em nosso país, o que é afirmado diretamente pelo único artigo sobre esse recurso .

Especificarei especificamente o seguinte material com relação ao trabalho no Windows, como o mais comum e usado, incluindo as instituições educacionais. Além disso, o uso de muitos programas gratuitos é uma dor aberta.

Se você pegar o pacote do Windows no site oficial do CalculiX, fica totalmente claro o que fazer em seguida. Em conjunto com a documentação em inglês, ele encerra esse produto para muitos e depois se traduz em comentários venenosos sobre a impossibilidade de seu uso. E em parte isso é verdade - o limite de entrada é realmente alto. Mas ainda vamos tentar.

Há várias versões não oficiais e relativamente iniciantes deste milagre para o Windows, entre elas o bConverged CalculiX for Windows . Fazemos o download do kit de distribuição a partir daqui , descompactamos e instalamos usando o método padrão "mais, mais ...". A instalação, portanto, não constitui um mistério especial e é bastante acessível a um usuário inexperiente. Como ambiente de trabalho principal, este pacote usa o editor de texto SciTE, que integra chamadas aos componentes do CalculiX, bem como a possibilidade de entrada interativa de comandos e é algo parecido com isso (clicável).

2. O problema da flexão de vigas e sua solução analítica usando métodos sopromat

Tome um problema simples do aluno - a flexão de uma viga de aço, uma das quais é comprimida, e a força vertical F é aplicada à outra.



Os parâmetros do problema são os seguintes: F = 10 kN; l = 1 m é o comprimento da viga; h = 0,1 me eb = 0,05 m são as dimensões da seção transversal. Por uma questão de simplicidade, não levaremos em consideração o peso do próprio feixe, pois ele, com um peso de 39 kg, é significativamente menor que a carga aplicada. Encontramos a tensão normal máxima na seção da viga e também calculamos a deflexão da viga devido à deformação por flexão.

Qualquer aluno que não tenha pulado um compromisso resolverá facilmente esse problema. Para não envergonhar os nobres donos, vou envolver todos os detalhes da decisão em um spoiler


Para quem tem preguiça de olhar por baixo do spoiler, darei a resposta imediatamente ao problema: a tensão normal máxima na seção do feixe $$$\ sigma_x = 119$ MPa, e a deflexão máxima é de 3,97 mm. Esses números são fornecidos para comparação subsequente com o que o procedimento para resolver esse problema no CalculiX nos fornecerá.

3. Preparação de geometria e grade computacional

Primeiro, você precisa inserir dados geométricos sobre a peça em questão no CalculiX. Sim, é possível exportar geometria de CADs, como é feito no mesmo ANSYS, mas passaremos por tortura e inseriremos a geometria manualmente. Abra o editor SciTE no kit bConverged e digite o seguinte texto

pnt p1 0 0 0
pnt p2 0.25 0 0
pnt p3 0.5 0 0
pnt p4 0.75 0 0
pnt p5 1.0 0 0

Salve o arquivo com o nome beam.fbd e pressione F10 para iniciar o pré-processamento. Veremos algo como o seguinte



O comando pnt cria um ponto no espaço com as coordenadas fornecidas e sua sintaxe é a seguinte

pnt [ ] [x] [y] [z]

Agora conecte esses pontos com linhas, adicionando o seguinte texto ao arquivo

line l1 p1 p2 25
line l2 p2 p3 25
line l3 p3 p4 25
line l4 p4 p5 25

depois de pressionar F10, a seguinte imagem



A equipe

line [ ] [ 1] [ 2] [ ]

cria uma linha conectando os pontos indicados nela, adicionando pontos intermediários que dividem a linha em um número especificado de segmentos (no nosso caso, 25 para cada linha). Isso será útil mais tarde para a geração de grade. Agora faça a finta com nossos ouvidos

seta lines l l1 l2 l3 l4
swep lines sweeplines tra 0 0 0.1 10

Primeira equipe

seta [ ] [ 1] ... [ N]

combina vários objetos em um conjunto com o nome fornecido. De fato, este é um análogo do agrupamento de objetos. Próximo comando

swep [ ] [ ] [ ] [, ] []

Move o conjunto de objetos selecionado para formar um novo conjunto. Objetos móveis são copiados. Nesse caso, o movimento dos pontos forma linhas, o movimento das linhas - superfícies, o movimento das superfícies - volumes contínuos. No nosso caso, alteramos o conjunto de linhas ao longo do eixo Z em 0,1 metros, enquanto as linhas resultantes são divididas em 10 segmentos. Pressionamos F10 ... er, e o que é?



Ghm, uma tela em branco ... É fácil de corrigir, basta adicionar linhas ao final do script

plot pa all
plus la all

Esses comandos dizem para você desenhar todos os pontos (pa) e adicionar todas as linhas (la) à tela, após o que obtemos esse resultado



Agora vamos criar superfícies com base no conjunto de linhas que criamos

seta surfaces s A001 A002 A003 A004

adicionando a exibição dessas superfícies no final do script

plus sa all




Agora vamos realizar outro deslocamento, agora ao longo do eixo Y por 0,05 metros, desenvolvendo todas as linhas formadas pelo deslocamento em 5 segmentos.

swep surfaces swepsurface tra 0.0 0.05 0.0 5

Consiga algo no espírito



A imagem resultante pode ser girada pressionando o botão esquerdo do mouse e, removendo a exibição de pontos e linhas, veremos algo inteligível



Sim ... o CalculiX está longe dos conceitos visuais usuais familiares ao usuário em massa, mas mesmo assim construímos a geometria do nosso feixe.

Geometria, geometria, mas para a geração de malha, daremos o próximo passo - remova todos os comandos plot e plus e envolva o código de geração de geometria nos comandos seto e setc, como este

seto beam
pnt p1 0 0 0
pnt p2 0.25 0 0
pnt p3 0.5 0 0
pnt p4 0.75 0 0
pnt p5 1.0 0 0
line l1 p1 p2 25
line l2 p2 p3 25
line l3 p3 p4 25
line l4 p4 p5 25
seta lines l l1 l2 l3 l4
swep lines sweeplines tra 0 0 0.1 10
seta surfaces s A001 A002 A003 A004
swep surfaces swepsurface tra 0 0.05 0 5
setc beam

Esse par de comandos combina toda a geometria criada em um determinado bloco de geometria com a viga de nome. Agora, esse grupo geométrico pode ser pulado na geração de malha, especificando depois de todo o código de comando acima

elty beam he8
mesh beam

- Gera uma grade que consiste em paralelepípedos (he8) com base em uma geometria chamada feixe. Agora imprima a malha gerada em um arquivo

send beam abq

- malha a saída para um arquivo chamado beam.msh no formato do pacote ABAQUS FEM (existe um pacote proprietário de cálculos do FEM e o CalculiX entende seu formato)



Assim, a grade é gerada, você pode olhar para o arquivo beam.msh e ver algo assim lá

*NODE, NSET=Nbeam
1,0.000000000000e+000,0.000000000000e+000,1.000000000000e-001
2,0.000000000000e+000,0.000000000000e+000,9.000000000000e-002
3,0.000000000000e+000,1.000000000000e-002,9.000000000000e-002
4,0.000000000000e+000,1.000000000000e-002,1.000000000000e-001
5,1.000000000000e-002,0.000000000000e+000,1.000000000000e-001
6,1.000000000000e-002,0.000000000000e+000,9.000000000000e-002
7,1.000000000000e-002,1.000000000000e-002,9.000000000000e-002
8,1.000000000000e-002,1.000000000000e-002,1.000000000000e-001
9,0.000000000000e+000,2.000000000000e-002,9.000000000000e-002
10,0.000000000000e+000,2.000000000000e-002,1.000000000000e-001
11,1.000000000000e-002,2.000000000000e-002,9.000000000000e-002
.
.
.
.
*ELEMENT, TYPE=C3D8, ELSET=Ebeam
1, 1, 2, 3, 4, 5, 6, 7, 8
2, 4, 3, 9, 10, 8, 7, 11, 12
3, 10, 9, 13, 14, 12, 11, 15, 16
4, 14, 13, 17, 18, 16, 15, 19, 20
5, 18, 17, 21, 22, 20, 19, 23, 24
6, 5, 6, 7, 8, 25, 26, 27, 28
7, 8, 7, 11, 12, 28, 27, 29, 30
8, 12, 11, 15, 16, 30, 29, 31, 32
9, 16, 15, 19, 20, 32, 31, 33, 34

Aparentemente, esta é uma lista de vértices dos elementos da grade com suas coordenadas, seguidos por uma lista de faces. Para tornar tudo mais bonito, usamos o modo interativo CalculiX. Para fazer isso, deixando a janela gráfica ativa , digite os seguintes comandos sequencialmente

plot f beam

- exibe todas as faces da geometria

view edge off

- desligar a exibição das bordas

view elem

- ativar a exibição de elementos da grade. Concluímos a entrada de cada comando pressionando Enter, os comandos inseridos são exibidos na janela SciTE no canto inferior direito, como este



Sim, você não pode chamar de super conveniente, mas, no entanto, temos uma imagem da malha gerada.



Observo que todos os pontos intermediários que foram criados ao criar a geometria se tornaram nós da malha. Assim, obtivemos uma grade hexagonal medindo 100 x 10 x 5 nós, com um tamanho de borda do elemento de 10 mm. O arquivo beam.fbd que criamos descreve a geometria do problema e o processo de criação da malha.

4. Estabelecendo limites

Um passo importante na aplicação do MEF é estabelecer restrições ao movimento de pontos estruturais, ou seja, levar em conta as restrições impostas a ele. No nosso caso, uma das extremidades da viga é comprimida e pode-se assumir que uma das extremidades é completamente estacionária. Precisamos dizer ao solucionador quais nós da malha FE estão imóveis. Pressionamos F10 quando o arquivo beam.fbd estiver aberto, aguarde a janela com a imagem do feixe aparecer



No modo interativo, insira o comando
rot -y
plot n beam

A primeira equipe implementa o modelo para que o eixo Y se afaste de nós, a segunda - inclui os nós de desenho (n) da malha FE. Movendo o modelo (segurando o botão direito do mouse) e redimensionando a imagem (segurando a roda do mouse) obtemos esta imagem



Agora precisamos selecionar todos os nós que queremos definir como fixos. Para fazer isso, usamos novamente o modo de entrada de dados interativo. Recrutamos uma equipe

qadd fixed

que começa a criar um conjunto de nós chamado fixo. O cursor na janela de desenho muda para o modo de seleção de elemento - ele é exibido na forma de uma seta com um pequeno quadrado. Coloque o cursor assim



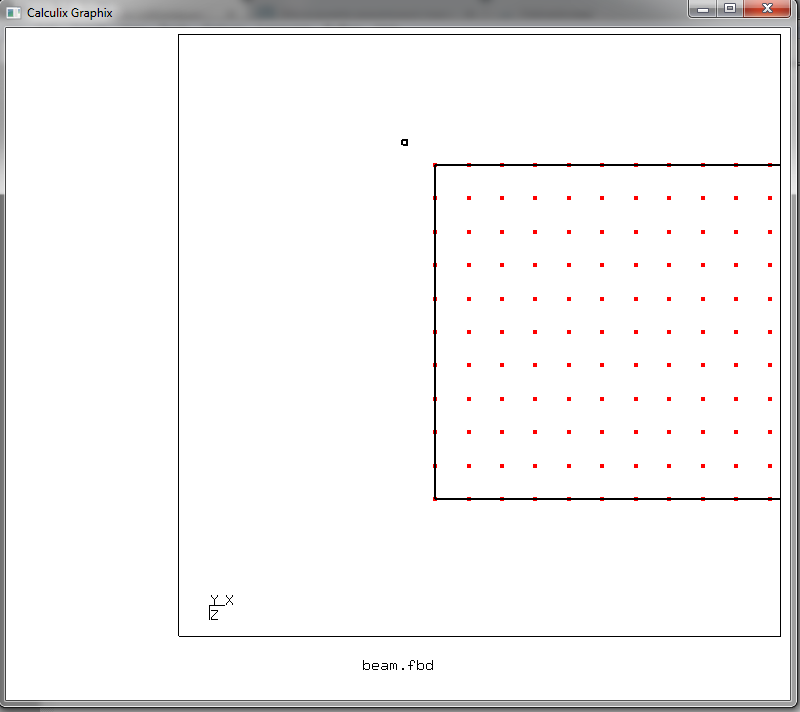
e pressione a tecla r. E então colocamos o cursor assim



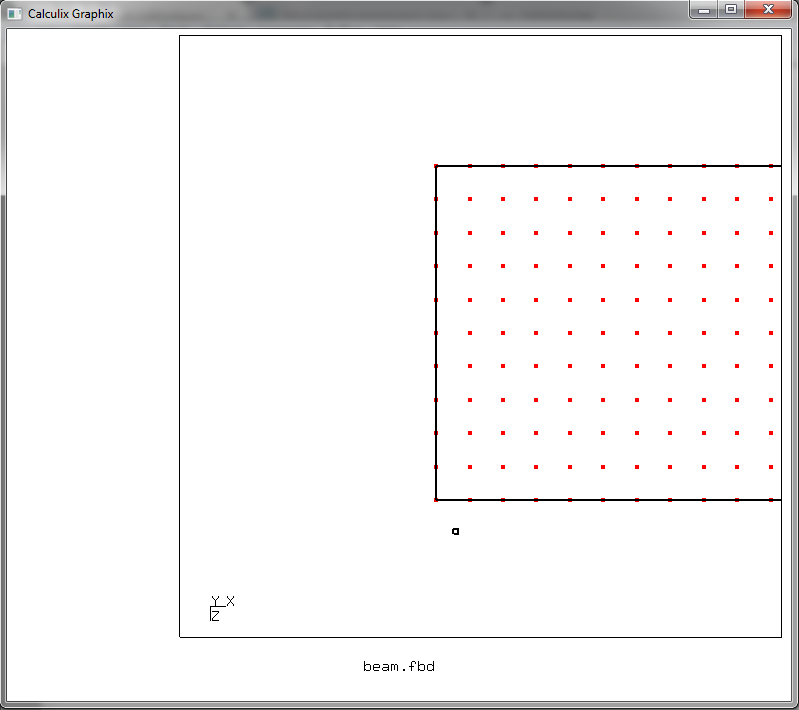
e pressione r novamente. Assim, formamos uma área de seleção de forma retangular, cuja diagonal é definida pelas posições do cursor marcadas ao pressionar r. Selecionamos com este retângulo os nós que precisamos no final da viga



pressione ae, em seguida, pressione n, realçando os nós marcados. Um calçado aparecerá na janela do console com uma lista de nós selecionados (a imagem é clicável)



Digite q para sair do modo de seleção e comando

plus n fixed g

para exibir os nós do grupo fixo em verde (g). Agora podemos ver quais nós serão incluídos na condição de fixação.



Agora devemos descarregar esses nós como um arquivo de restrição, que é subsequentemente alimentado na entrada do solucionador. Para fazer isso, digite o comando

send fixed abq spc 123

- descarregue um grupo de nós fixos na forma de um arquivo de restrição no formato ABAQUS (abq), restringindo o movimento de todos os nós do grupo em todos os três graus de liberdade (1 eixo X, 2 eixos Y, 3 eixos Z). Como resultado, o arquivo fixed_123.bou é formado, com o seguinte conteúdo

** BOUNDARY based on fixed
1, 1, ,
2, 1, ,
3, 1, ,
4, 1, ,
9, 1, ,
10, 1, ,
13, 1, ,
14, 1, ,
17, 1, ,
.
.
.


- de fato, é uma enumeração de todos os nós e o número do grau de liberdade pelo qual o movimento de um determinado nó é limitado.

5. Atribuição de cargas

Depois de fixarmos a viga, tentaremos carregá-la. Ligue a exibição de faces e elementos novamente

plot f beam
view edge off
view elem

Oriente a imagem para que possamos ver a parte superior da extremidade solta do feixe



Vamos mudar para o modo de seleção de objetos

qadd load

Coloque o cursor na face desejada e pressione f



O rosto é destacado em roxo e uma descrição aparece na janela do console que é adicionada ao conjunto de carregamento.

qadd load
2541 e:3873 s:6 n= 5298 5310 5312 5300

Pressione a para finalizar a formação do aparelho, pressione q para sair do modo de seleção. Aplicamos pressão na face selecionada que fornece uma força resultante de 10000 N. É fácil calcular que a área da face selecionada é de 1 cm ² , o que significa que a pressão desejada é 10 ⁸ Pa. Defina esta carga com o comando

send load abq pres 1e8

- exibe a carga no arquivo load.dlo no formato ABAQUS. O arquivo fica assim

** Pressure based on load
3873, P6, 100000000.000000

O número do elemento da malha, sua face e o valor da pressão nessa face são indicados. Assim, a preparação dos dados iniciais pode ser considerada concluída.

6. Descrição dos dados de entrada e o lançamento do solucionador

Todos esses dados - a grade, limitações e cargas, devem agora ser puxados para a entrada do solucionador FEM, para o qual formamos um arquivo de entrada desse tipo

beam.inp
*HEADING
Model: CalculiX Beam Input File for Habrahabr article
*INCLUDE,INPUT=beam.msh
*BOUNDARY
*INCLUDE,INPUT=fixed_123.bou
*MATERIAL,NAME=EL
*ELASTIC
2e11,0.3
*SOLID SECTION,ELSET=Ebeam,MATERIAL=EL
*STEP
*STATIC
*DLOAD
*INCLUDE,INPUT=load.dlo
*NODE FILE
U
*EL FILE
S
*END STEP


Vou explicar com mais detalhes o que é o quê. Primeira seção do arquivo

*HEADING
Model: CalculiX Beam Input File for Habrahabr article
*INCLUDE,INPUT=beam.msh

define a descrição da tarefa e inclui um arquivo com o CE-mesh beam.msh. A próxima seção forma as condições de contorno - aquelas relações que definimos no arquivo fixed_123.bou

*BOUNDARY
*INCLUDE,INPUT=fixed_123.bou


Não devemos esquecer o material que definimos como elástico, determinando o módulo de Young e a razão de Poisson. Tomamos os valores médios para aços estruturais

*MATERIAL,NAME=EL
*ELASTIC
2e11,0.3
*SOLID SECTION,ELSET=Ebeam,MATERIAL=EL

A última seção define o tipo de tarefa - o cálculo do carregamento estático e as cargas do arquivo load.dlo que são

*STEP
*STATIC
*DLOAD
*INCLUDE,INPUT=load.dlo
*NODE FILE
U
*EL FILE
S
*END STEP


Após verificar se temos uma guia no SciTE com o arquivo beam.inp, pressione Ctrl + F10, iniciando o solucionador. Temos uma exaustão nos dizendo que o CalculiX calculou algo para nós lá. Exaustão, para não bagunçar o texto que trago embaixo do spoiler

7. Pós-processamento e análise de decisão

Os resultados obtidos pelo solucionador requerem processamento pelo pós-processador. Para chamá-lo, pressione Shift + F10 e obtenha uma janela gráfica com a imagem da viga. Clique no lado esquerdo desta janela, fora do quadro com a imagem da viga e acesse o menu



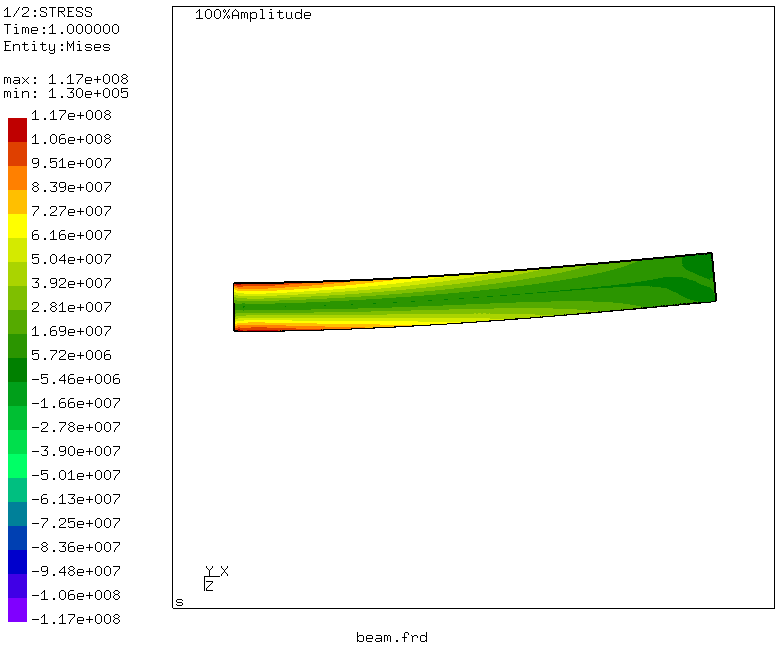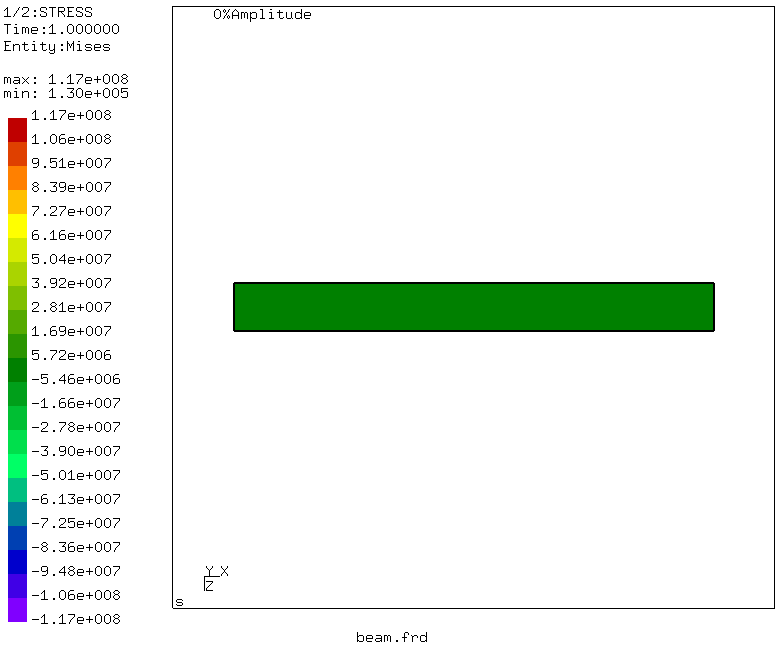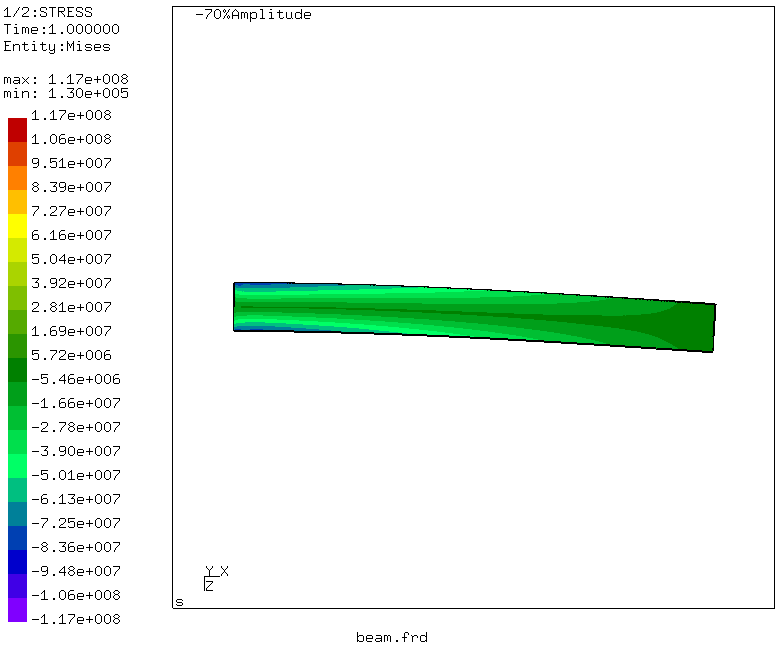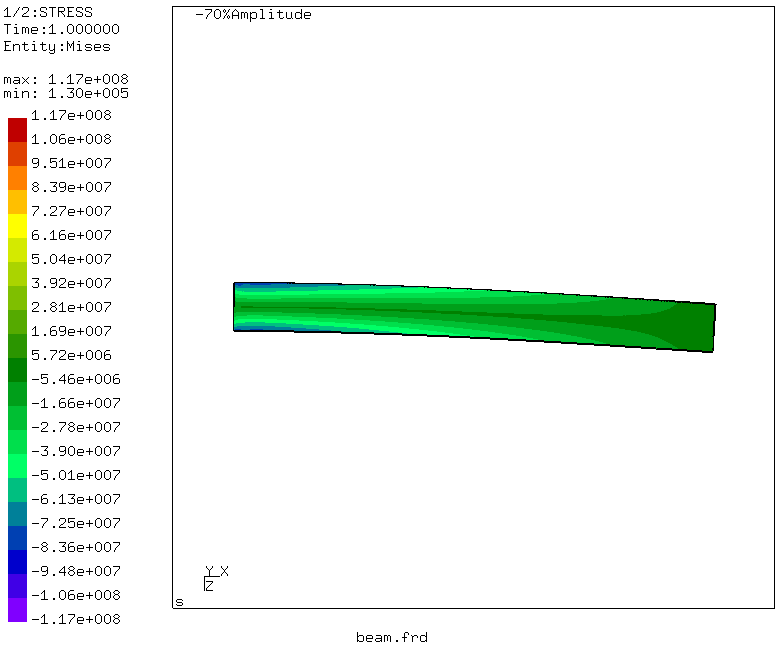
O que nos interessa? Tensões nas seções da viga - selecione Conjuntos de dados -> STRESS. O menu desaparecerá, mas o chamamos novamente e selecionamos Conjuntos de dados -> Entidades -> Mises. Como resultado, o modo de tensão equivalente de von Mises é ativado.



Então - o momento da verdade! A tensão máxima equivalente na seção da viga é de 117 MPa, o que difere um pouco do resultado do comprometimento. Mas! Resolvendo o problema da sopromat, não levamos em consideração as tensões tangenciais durante a flexão e o cisalhamento, mas calculamos apenas as tensões normais da flexão. O que acontecerá com a deflexão? Vá para o menu: Conjuntos de dados -> DISP e Conjuntos de dados -> Entidades -> D3



Observamos que o deslocamento máximo corresponde à extremidade carregada da viga e é igual a 3,96 milímetros! Magnífico e correlacionado com nosso cálculo usando a integral de Mohr.

Por manipulações simples, que podem ser lidas aqui , também é gerada uma animação de deformações de feixe.

Tirar conclusões

"Uh, cara, espere um minuto, o que vem a seguir ?!" Hmm, o homem não pode incluir em um artigo toda a variedade de questões que surgem quando mencionamos o FEM em geral, e o CalculiX em particular. O artigo acabou por ser volumoso e bastante chato. E seu objetivo é explicar duas coisas em uma linguagem inteligível:

1. Open Source não passou pelo software de análise FEM
2. Estudar e usar este software não é tão difícil quanto pode parecer à primeira vista

O suficiente para um artigo de revisão? Eu acho que sim. Na preparação do artigo, foram utilizadas as seguintes fontes:

1. Calculix FEA Beam - serviu de base para todo o material apresentado. Como a experiência adquirida pelo autor foi adicionada aqui e todo o código foi escrito por ele durante a redação do artigo, isso não é uma tradução, ou seja, um tutorial em russo
2. Manual Oficial do CalculiX

Código de exemplo está disponível no Gitlab .

Concluindo, observo - não sou forte, não tive um compromisso na universidade. Um pouco mais tarde, a vida (e o amor!) Me forçaram a conhecer seus próprios fundamentos. Então, talvez, erros estejam presentes no texto, sobre o qual estou esperando comentários maliciosos e prometo levar em consideração todos os comentários.

Obrigado pela atenção!