Números de ponto flutuante do oeste selvagem mais rápidos

No processo de implementação de um "leitor", surgiu um problema com maior precisão nos cálculos. O algoritmo de cálculo trabalhou rapidamente em números de ponto flutuante padrão, mas quando as bibliotecas para cálculos precisos foram conectadas, tudo começou a desacelerar descontroladamente. Neste artigo, consideraremos algoritmos para expandir números de ponto flutuante usando uma abordagem de múltiplos componentes, devido à qual foi possível obter aceleração, já que a aritmética de flutuação é implementada em um chip cp. Essa abordagem será útil para o cálculo mais preciso da derivada numérica, inversão de matriz, corte de polígono ou outros problemas geométricos. Portanto, é possível emular a flutuação de 64 bits em placas de vídeo que não as suportam.

1. Introdução

Como Nikluas Wirth nos legou para manter os números 0 e 1, nós os armazenamos neles. E é que os seres humanos vivem no sistema decimal, e os números aparentemente comuns 0.1 e 0.3 não são representáveis ​​no sistema binário por uma fração finita? Sentimos um choque cultural quando fazemos cálculos sobre eles. Obviamente, estão sendo feitas tentativas para criar bibliotecas para processadores baseados no sistema decimal e o IEEE tem até formatos padronizados.

Mas, por enquanto, levamos em consideração o armazenamento binário em todos os lugares e fazemos todos os cálculos de dinheiro com as bibliotecas para cálculos exatos, como bignumber, o que leva à perda de desempenho. Asiks consideram criptografia e, nos processadores, há muito pouco espaço para essa sua aritmética decimal, dizem os profissionais de marketing. Portanto, uma abordagem multicomponente, quando um número é armazenado na forma de uma soma não transformada de números, é um truque conveniente e uma esfera em desenvolvimento ativo no campo da informática teórica. Embora Decker ainda tenha aprendido a se multiplicar corretamente, sem perda de precisão, em 1971, as bibliotecas prontas para uso apareceram muito mais tarde (MPFR, QD) e não em todos os idiomas, aparentemente porque nem todos os padrões IEEE são compatíveis, mas provas rigorosas de erro de cálculo ainda mais tarde, por exemplo em 2017 para aritmética de duas palavras.

Aritmética de duas palavras

Qual é o objetivo? Em tempos de barba, quando não havia padrões para números flutuantes, para evitar problemas com a implementação do arredondamento, Møller surgiu e Knuth mais tarde provou que existe um somatório sem erros. Correndo dessa maneira

function quickTwoSum(a, b) { let s = a + b; let z = s - a; let e = b - z; return [s, e]; } 

Nesse algoritmo, assumiu-se que se $$$| a | > | b |$, sua soma exata pode ser representada como a soma de dois números $$$s + e$e você pode armazená-los em pares para cálculos subsequentes, e a subtração é reduzida à adição com um número negativo.



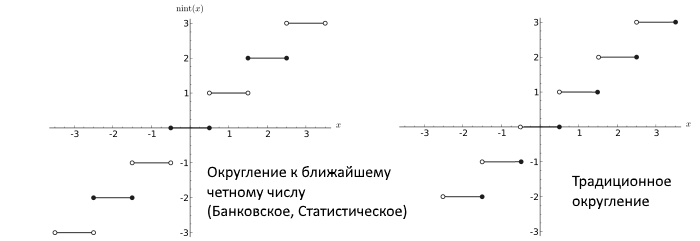
Posteriormente, Dekker mostrou que, se forem usados ​​números de ponto flutuante, use o arredondamento para o número par mais próximo (vínculos entre o mais próximo e o mais par, o que geralmente é um procedimento correto que não leva a grandes erros no processo de cálculos longos e no padrão IEEE), existe um algoritmo de multiplicação sem erros.

 function twoMult(a, b) { let A = split(a); let B = split(b); let r1 = a * b; let t1 = -r1 + A[0] * B[0]; let t2 = t1 + A[0] * B[1]; let t3 = t2 + A[1] * B[0]; return [r1, t3 + A[1] * B[1]]; } 

onde split () é o algoritmo do Sr. Weltkamp para dividir um número

 let splitter = Math.pow(2, 27) + 1; function split(a) { let t = splitter * a; let d = a - t; let xh = t + d; let xl = a - xh; return [xh, xl]; } 

usando constante $$$C = 2 ^ s + 1$que equivale a pouco mais da metade do comprimento da mantissa, o que não leva ao excesso de números no processo de multiplicação e divide a mantissa em duas metades. Por exemplo, com um comprimento de palavra de 64 bits, o comprimento da mantissa é 53 e depois s = 27.



Dessa maneira, Dekker forneceu o conjunto quase completo necessário para a computação em aritmética de duas palavras. Desde lá, também foi indicado como multiplicar, dividir e quadrado dois números de duas palavras.

Seu algoritmo quickTwoSum para somar duas palavras duplas estava em toda parte "inline" e a verificação foi usada $$$| a | > | b |$. Nos processadores modernos, como descrito em [4], é mais barato usar operações adicionais com números do que ramificar o algoritmo. Portanto, o algoritmo a seguir agora é mais apropriado para adicionar dois números de uma única palavra

 function twoSum(a, b) { let s = a + b; let a1 = s - b; let b1 = s - a1; let da = a - a1; let db = b - b1; return [s, da + db]; } 

E, portanto, este é o somatório e a multiplicação de números de duas palavras.

 function add22(X, Y) { let S = twoSum(X[0], Y[0]); let E = twoSum(X[1], Y[1]); let c = S[1] + E[0]; let V = quickTwoSum(S[0], c); let w = V[1] + E[1]; return quickTwoSum(V[0], w); } function mul22(X, Y) { let S = twoMult(X[0], Y[0]); S[1] += X[0] * Y[1] + X[1] * Y[0]; return quickTwoSum(S[0], S[1]); } 

De um modo geral, a lista mais completa e precisa de algoritmos para aritmética de duas palavras, limites teóricos de erros e implementação prática é descrita no link [3] de 2017. Portanto, se estiver interessado, eu recomendo ir direto para lá. Em geral, um algoritmo para palavras quadruplicadas é apresentado em [6] e em [5] para uma extensão multicomponente de comprimento arbitrário. Somente lá, após cada operação, o processo de renormalização é usado, o que nem sempre é ideal para tamanhos pequenos, e a precisão dos cálculos no QD não é estritamente definida. Em geral, vale a pena pensar nos limites de aplicabilidade dessas abordagens, é claro.

Histórias de terror javascript-a. Comparação de decimal.js vs bignumber.js vs big.js.

Aconteceu que quase todas as bibliotecas para cálculos exatos em js foram escritas por uma pessoa. A ilusão da escolha é criada, embora quase todas sejam iguais. Além disso, a documentação não afirma explicitamente que, se você não arredondar números após cada operação de multiplicação / divisão, o tamanho do seu número dobrará o tempo todo e a complexidade do algoritmo poderá se tornar fácil em x3500. Por exemplo, uma comparação do tempo de cálculo pode ser assim se você não arredondar os números.



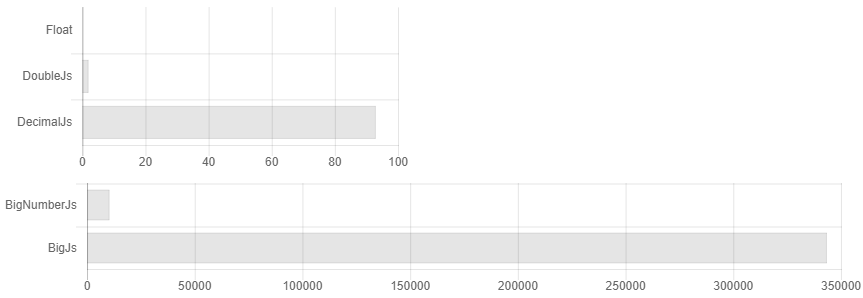
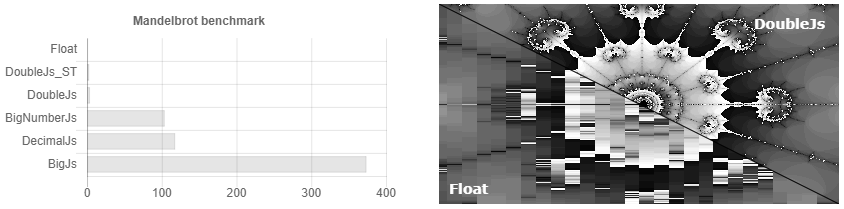
Ou seja, você define a precisão para 32 casas decimais e ... Opa, você já tem 64 dígitos, 128. Pensamos com muita precisão! 256, 512 ... Mas eu defino 32! .. 1024, 2048 ... Algo assim aparece no alto 3.500 vezes. A documentação afirma que, se você tiver cálculos científicos, provavelmente o decimal.js é melhor para você. Embora, de fato, se você arredondar periodicamente, para cálculos científicos, o Bignumber.js funcione um pouco mais rápido (veja a Fig. 1). Quem precisa contar os centésimos de um centavo se eles não podem ser trocados? Existe algum caso em que preciso armazenar mais números indicados e não consigo sair com alguns caracteres extras? Como leva o seno de um número tão monstruoso, quando ninguém sabe a estrita precisão da convergência da série Taylor para números arbitrários? Em geral, não há suspeitas infundadas de que é possível aumentar a velocidade de cálculo lá, usando algoritmos de multiplicação de Schoenhage-Strassen e encontrando o seno com cálculos Cordic, por exemplo.

Double.js

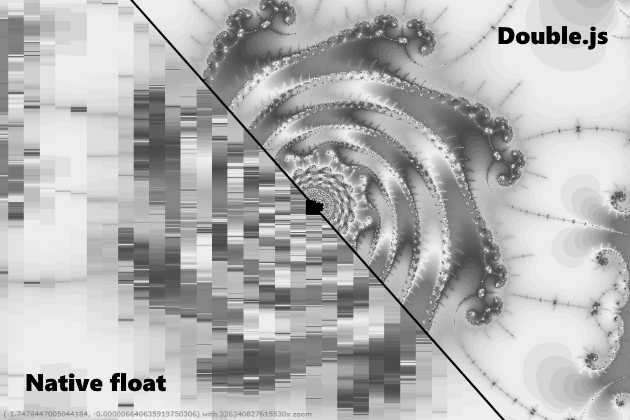
Gostaria de dizer, é claro, que o Double.js conta com rapidez e precisão. Mas isso não é inteiramente verdade, ou seja, é 10 vezes mais rápido que considere, mas nem sempre é preciso. Por exemplo, 0,3-0,1 ele pode processar, passando para armazenamento duplo e vice-versa. Mas o número Pi pode ser resolvido com uma precisão dupla de quase 32 dígitos e não dá certo. Um erro é gerado no dia 16, como se um estouro estivesse ocorrendo. Em geral, exorto a comunidade js a trabalhar em conjunto para tentar resolver o problema de análise, pois estou emperrado. Tentei analisar digitalmente e dividir em dupla precisão, como em QD, dividir em lotes de 16 dígitos e dividir em dupla precisão, dividir a mantissa usando Big.js como em uma das bibliotecas de Julia. Agora peço um erro em .parseFloat (), já que os padrões IEEE com arredondamento para o número inteiro mais próximo são suportados, mesmo com o ECMAScript 1. Embora, é claro, você possa tentar ligar o buffer binário e assistir a cada 0 e 1. Em geral, se você puder resolver esse problema, então será possível fazer cálculos com precisão arbitrária com aceleração em x10-x20 a partir de bignumber.js. No entanto, muitos Mandelbrot já oferecem qualidade e você pode usá-lo para tarefas geométricas.

Um ano depois, voltei para cá e ainda corrigi um problema com a análise. O problema estava apenas com precisão insuficiente, quando multiplicado por 10 ^ (- n). Todos os algoritmos foram revisados ​​do zero e agora são executados com uma precisão e velocidade assustadoras.



Aqui está um link para a lib , há uma referência interativa e uma sandbox onde você pode brincar com ela.

Fontes utilizadas

1. O. Møller. Quase precisão dupla na aritmética de ponto flutuante. 1965.
2. Theodorus Dekker. Uma técnica de ponto flutuante para estender a precisão disponível , 1971. [ Viewer ]
3. Mioara Joldes, Jean-Michel Muller, Valentina Popescu. Limites de erro rigorosos e rigorosos para blocos de construção básicos da aritmética de duas palavras , 2017. [ PDF ]
4. Muller, J.-M. Brisebarre, N. de Dinechin, etc. Manual de Aritmética de Ponto Flutuante, Capítulo 14, 2010.
5. Jonathan Shewchuk. Predicados geométricos de ponto flutuante adaptável robusto , 1964. [ PDF ]
6. Yozo Hida, Xiaoye Li e David Bailey. Biblioteca de Aritmética Duplo-Duplo e Quad-Duplo , 2000. [ PDF ]