Em que desenhar imagens vetoriais? Para mim, como para muitos outros, a resposta é bastante óbvia: provavelmente no ilustrador. Bem, ou no Inskape. Também pensei quando me pediram para desenhar oitocentas peças para um livro de física. Nada disso, apenas ilustrações técnicas em preto e branco com todos os tipos de blocos, bolas, molas, lentes, carros, tratores e similares. Supunha-se que o livro fosse feito em latech, e eu recebi arquivos do Word com imagens inseridas - em esboços a lápis ou digitalizações de outros livros - e o manuscrito parecia estar de alguma forma. Nesse caso, o primeiro pensamento - atrair o inscape - sucumbiu às fantasias sobre o tópico "como isso automatizaria tudo?" Por alguma razão, o
MetaPost parecia ser a melhor opção naquele momento.
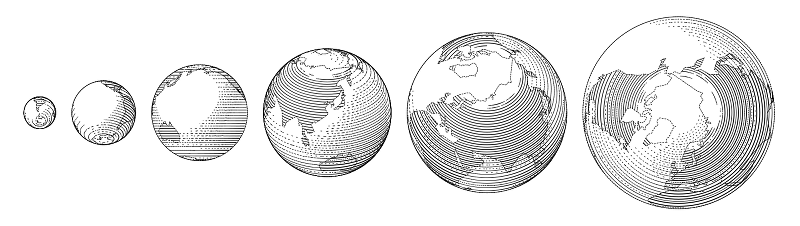
A vantagem mais significativa dessa solução é que cada imagem pode ser uma pequena função de várias variáveis; é fácil, por exemplo, alterar esse tamanho e ajustar as faixas a circunstâncias específicas previamente desconhecidas sem violar proporções importantes, o que é difícil de obter com meios mais tradicionais. E os elementos repetidos - as próprias bolas e molas - podem ser feitos para se comportar muito mais interessantes do que os meios dos editores de vetores "humanos" permitem.
Eu queria fazer fotos com incubação, como a encontrada em livros antigos.

Primeiro, tivemos que obter linhas de espessura variável. A principal dificuldade aqui é construir uma curva que seja mais ou menos paralela à determinada e, conforme necessário, altere a distância para a determinada. Eu confiei na maneira mais, provavelmente, a mais primitiva em que os segmentos que conectam os pontos intermediários da curva de Bezier são simplesmente transportados a uma dada distância em paralelo. Com a diferença de que essa distância pode variar ao longo da curva.
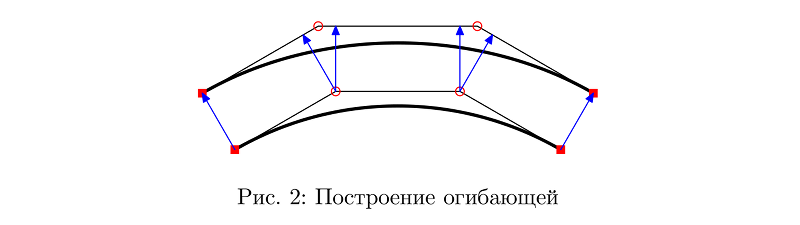
Na maioria dos casos, isso permite um resultado decente.
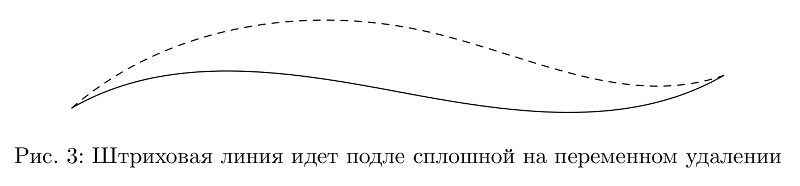
Código de exemploDaqui em diante, assume-se que a biblioteca foi
baixada e em algum lugar existe a linha
input fiziko.mp; . A maneira mais rápida de iniciar e procurar no ConTeXt (em seguida,
beginfig e
endfig não
endfig necessários):
\starttext
\startMPcode
input fiziko.mp;
\stopMPcode
\stoptext
ou no LuaLaTeX:
\documentclass{article}
\usepackage{luamplib}
\begin{document}
\begin{mplibcode}
input fiziko.mp;
\end{mplibcode}
\end{document}
beginfig(3);
path p, q; % , , ,
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q := offsetPath(p)(1cm*sin(offsetPathLength*pi)); % — , — (offsetPathLength, 0 1), ,
draw p;
draw q dashed evenly;
endfig;
Agora, duas dessas curvas podem ser usadas para fazer um contorno de uma linha de espessura variável.

Código de exemplobeginfig(4);
path p, q[];
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
q1 := offsetPath(p)(1/2pt*(sin(offsetPathLength*pi)**2)); %
q2 := offsetPath(p)(-1/2pt*(sin(offsetPathLength*pi)**2)); %
fill q1--reverse(q2)--cycle;
endfig;
A espessura deve ser um pouco limitada por baixo, caso contrário, a varredura assumirá partes muito finas das linhas ao imprimir, e isso geralmente não é muito bonito. Uma opção é desenhar todas as linhas, cuja espessura é menor que algum valor, com linhas tracejadas da mesma espessura mínima, de modo que a quantidade total de tinta por unidade de comprimento, em média, corresponda à da linha da espessura de destino. Ou seja, em vez de reduzir a quantidade de tinta pelas laterais da linha, comece a roê-la com listras transversais.

Código de exemplobeginfig(5);
path p;
p := (0,-1/4cm){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 1/4cm);
draw brush(p)(1pt*(sin(offsetPathLength*pi)**2)); % , ,
endfig;
Agora você pode desenhar bolas. Podem ser apenas círculos concêntricos, cuja espessura das linhas é determinada pela função da iluminação da bola nos pontos pelos quais as linhas passam.
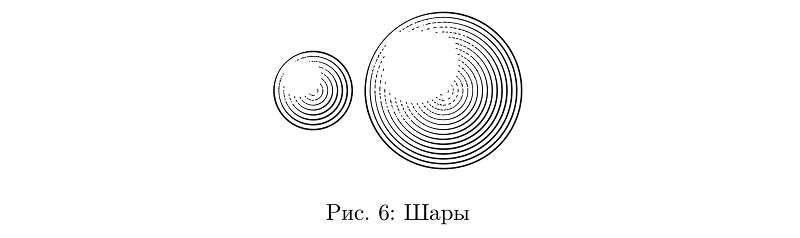
Código de exemplobeginfig(6);
draw sphere.c(1.2cm);
draw sphere.c(2.4cm) shifted (2cm, 0);
endfig;
Outro primitivo conveniente são as "mangueiras": grosso modo, cilindros que podem ser dobrados de qualquer maneira. Enquanto eles são de seção transversal constante, tudo é simples com eles.
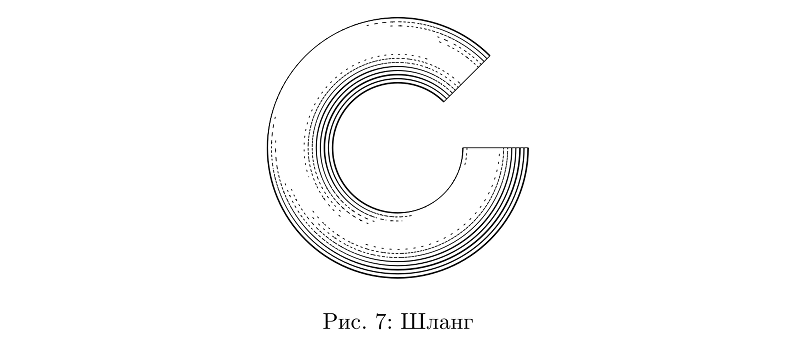
Código de exemplobeginfig(7);
path p;
p := subpath (1,8) of fullcircle scaled 3cm;
draw tube.l(p)(1/2cm); % — ,
endfig;
Se a espessura for alterada, o número de traços deverá ser alterado de acordo, mantendo a densidade média de preenchimento inalterada e também leve em consideração as alterações de espessura ao calcular a iluminação.
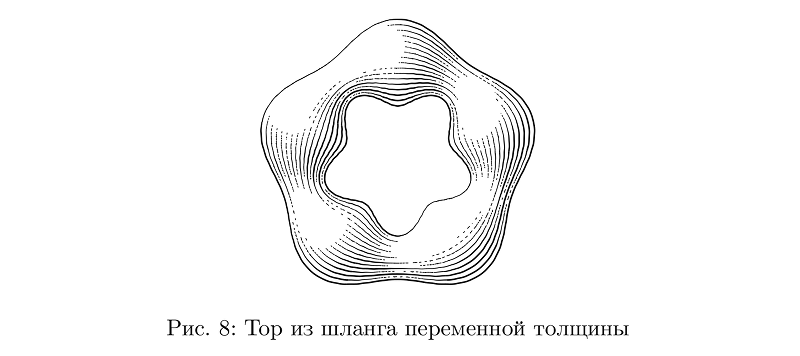
Código de exemplobeginfig(8);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm;
draw tube.l(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
Ainda existem mangueiras com hachura transversal, mas para elas era mais difícil resolver o problema de preservar a densidade média de preenchimento, portanto, em muitos casos, elas ainda não parecem muito boas.
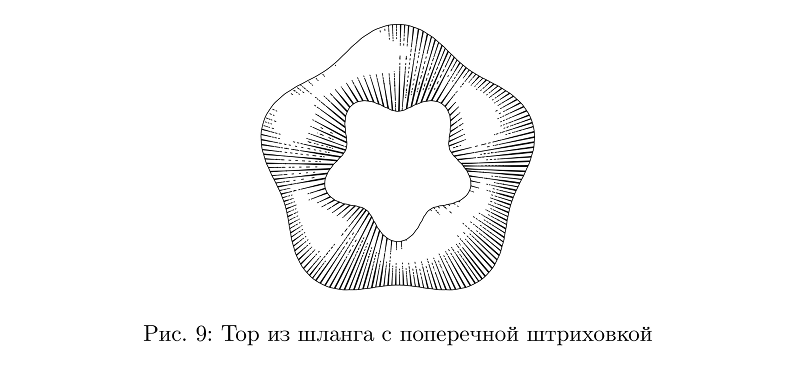
Código de exemplobeginfig(9);
path p;
p := pathSubdivide(fullcircle, 2) scaled 3cm;
draw tube.t(p)(1/2cm + 1/6cm*sin(offsetPathLength*10pi));
endfig;
Em princípio, muitas coisas podem ser feitas apenas com mangueiras: de cones e cilindros a balaústres.
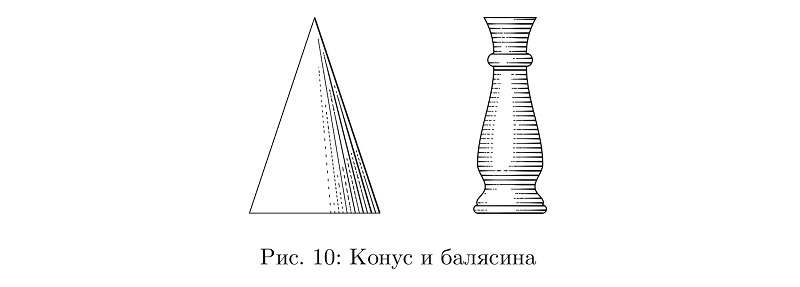
Código de exemplobeginfig(10);
draw tube.l ((0, 0) -- (0, 3cm))((1-offsetPathLength)*1cm) shifted (-3cm, 0); %
path p;
p := (-1/2cm, 0) {dir(175)} .. {dir(5)} (-1/2cm, 1/8cm) {dir(120)} .. (-2/5cm, 1/3cm) .. (-1/2cm, 3/4cm) {dir(90)} .. {dir(90)}(-1/4cm, 9/4cm){dir(175)} .. {dir(5)}(-1/4cm, 9/4cm + 1/5cm){dir(90)} .. (-2/5cm, 3cm); %
p := pathSubdivide(p, 6);
draw p -- reverse(p xscaled -1) -- cycle;
tubeGenerateAlt(p, p xscaled -1, p rotated -90); % , tube.t, — — , — .
endfig;
Parte do que pode ser construído com essas partes está na biblioteca. Digamos que um globo é basicamente uma bola.
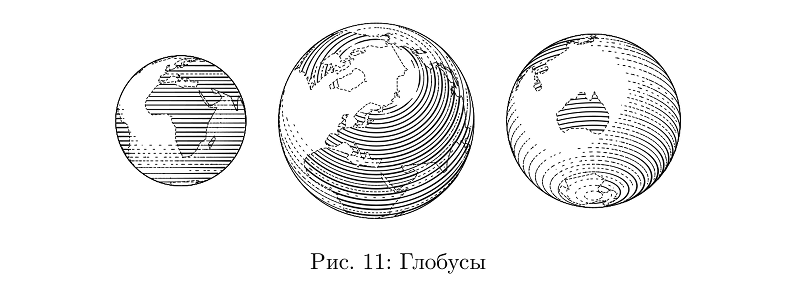
Código de exemplobeginfig(11);
draw globe(1cm, -15, 0) shifted (-6/2cm, 0); % , ,
draw globe(3/2cm, -30.28367, 59.93809);
draw globe(4/3cm, -140, -30) shifted (10/3cm, 0);
endfig;
Embora não: aqui a eclosão ocorre paralelamente e o controle da espessura do curso para manter a densidade do preenchimento é ainda mais difícil do que no caso da eclosão transversal nas mangueiras, portanto esse é um tipo separado de bola.
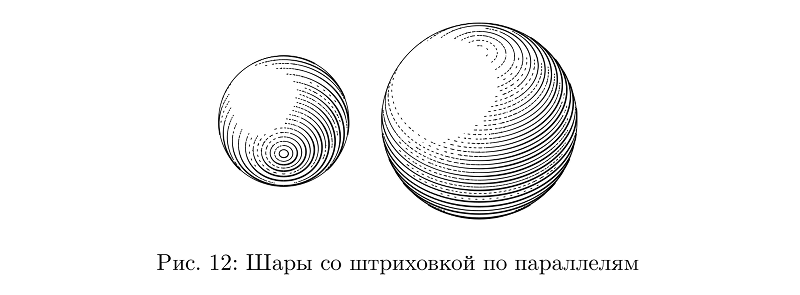
Código de exemplobeginfig(12);
draw sphere.l(2cm, -60); %
draw sphere.l(3cm, 45) shifted (3cm, 0);
endfig;
E o peso é um projeto direto de dois tipos de mangueiras de espessura variável.
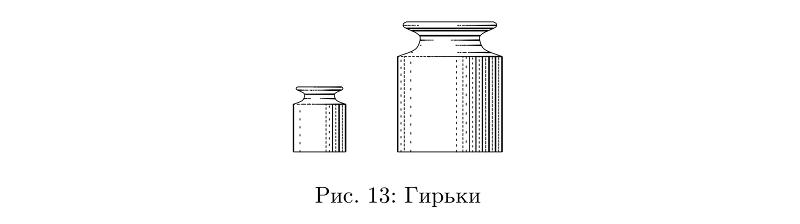
Código de exemplobeginfig(13);
draw weight.s(1cm); %
draw weight.s(2cm) shifted (2cm, 0);
endfig;
Ainda existe uma ferramenta para amarrar as mangueiras em nós.
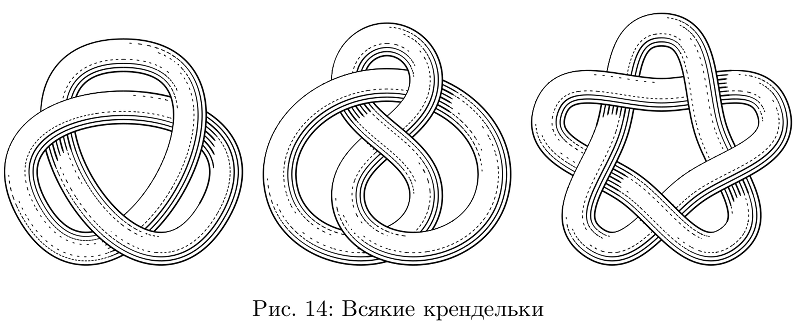
Código de amostra para não bagunçar, apenas um nóbeginfig(14);
path p;
p := (dir(90)*4/3cm) {dir(0)} .. tension 3/2 ..(dir(90 + 120)*4/3cm){dir(90 + 30)} .. tension 3/2 ..(dir(90 - 120)*4/3cm){dir(-90 - 30)} .. tension 3/2 .. cycle;
p := p scaled 6/5;
addStrandToKnot (primeOne) (p, 1/4cm, "l", "1, -1, 1"); % primeOne , p 1/4cm, "l" ( tube.l, tube.t ) «» "1, -1, 1" p
draw knotFromStrands (primeOne); % .
endfig;
As sombras dos nós são uma complicação no modelo de iluminação. Em princípio, ninguém se preocupa em usá-los em outros casos, mas eu não estabeleci uma meta de aprofundar o volume; portanto, embora isso não seja muito conveniente, não funciona em todos os lugares.
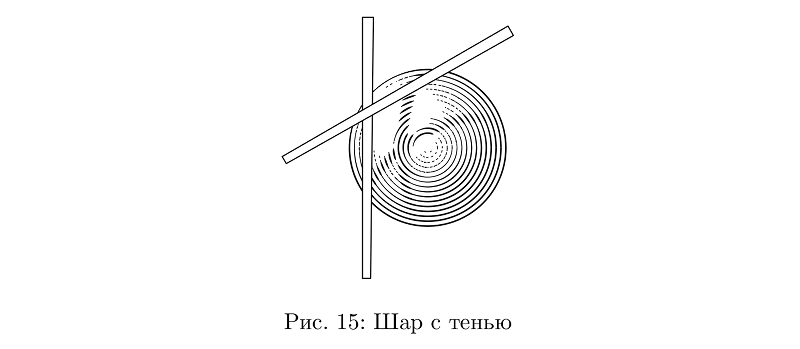
Código de exemplobeginfig(15);
path shadowPath[];
boolean shadowsEnabled;
numeric numberOfShadows;
shadowsEnabled := true; %
numberOfShadows := 1; %
shadowPath0 := (-1cm, -2cm) -- (-1cm, 2cm) -- (-1cm +1/6cm, 2cm) -- (-1cm + 1/8cm, -2cm) -- cycle; % , ,
shadowDepth0 := 4/3cm; % - «» ,
shadowPath1 := shadowPath0 rotated -60;
shadowDepth1 := 4/3cm;
draw sphere.c(2.4cm); % sphere.c tube.l
fill shadowPath0 withcolor white;
draw shadowPath0;
fill shadowPath1 withcolor white;
draw shadowPath1;
endfig;
E, claro, você precisa de uma textura de madeira. A influência da natureza do crescimento de nós no padrão das seções dos anéis das árvores é um tópico para pesquisas sérias. Muito simplificando, podemos imaginar anéis anuais em planos paralelos nos quais as distorções dos nós se introduzem. Portanto, basta descrever a mudança no plano por alguma função não muito sofisticada (a função nó) e considerar uma série de isolinhas para a soma do conjunto de funções como o padrão desejado de anéis de árvores.
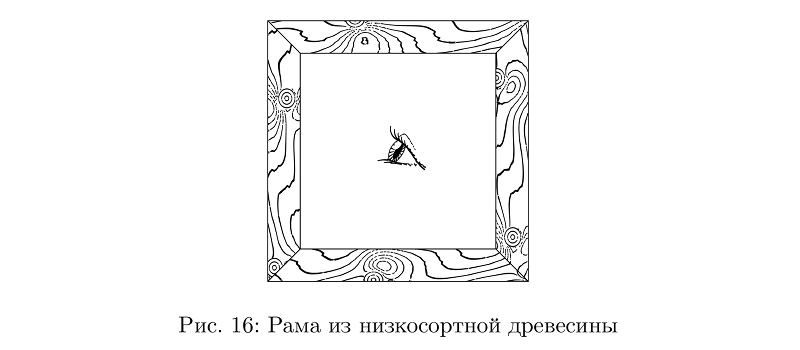
Código de exemplobeginfig(16);
numeric w, b;
pair A, B, C, D, A', B', C', D';
w := 4cm;
b := 1/2cm;
A := (0, 0);
A' := (b, b);
B := (0, w);
B' := (b, wb);
C := (w, w);
C' := (wb, wb);
D := (w, 0);
D' := (wb, b);
draw woodenThing(A--A'--B'--B--cycle, 0); % , A--A'--B'--B--cycle, 0
draw woodenThing(B--B'--C'--C--cycle, 90);
draw woodenThing(C--C'--D'--D--cycle, 0);
draw woodenThing(A--A'--D'--D--cycle, 90);
eyescale := 2/3cm; %
draw eye(150) shifted 1/2[A,C]; % 150
endfig;
O olho da figura acima pode abrir um pouco, depois apertar os olhos e a largura da pupila muda. Não há um significado especial nisso, mas resulta mais vividamente do que se tais ninharias fossem mecanicamente iguais em todos os lugares.

Código de exemplobeginfig(17);
eyescale := 2/3cm; % 1/2cm
draw eye(0) shifted (0cm, 0);
draw eye(0) shifted (1cm, 0);
draw eye(0) shifted (2cm, 0);
draw eye(0) shifted (3cm, 0);
draw eye(0) shifted (4cm, 0);
endfig;
Na maioria das vezes, as imagens não eram muito complicadas, mas se você abordar o assunto com toda a seriedade, muitas tarefas deverão ser resolvidas para ilustrá-las de maneira significativa. Aqui, digamos, a tarefa de Lopital sobre o bloco (não sei como é chamado corretamente em russo, não estava no livro, é apenas um exemplo): o bloco fica pendurado em uma corda de comprimento suspensa no ponto A, está presa em outra corda suspensa na mesma altura no ponto B, a carga C. fica pendurada na segunda corda, e a questão é: se as cordas e o bloco não têm peso, onde estará a carga? Surpreendentemente, tanto a solução do problema quanto a construção não são tão elementares, mas, jogando com várias variáveis, você pode facilmente fazer a imagem exatamente o que ficará melhor na tira, enquanto permanece verdadeiro.
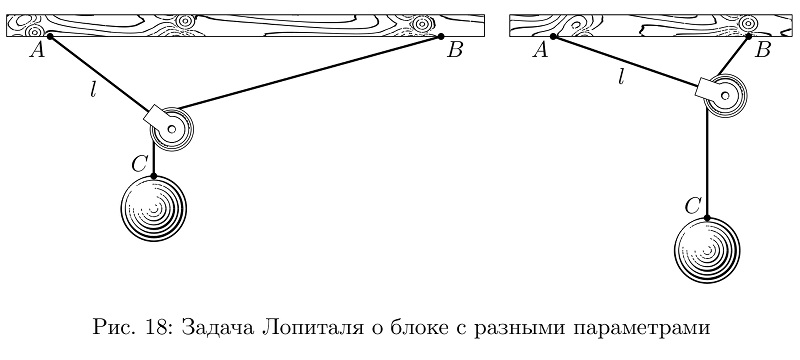
Código de exemplovardef lHopitalPulley (expr AB, l, m) = % AB l, m . ? : , , arithmetic overflow.
save A, B, C, D, E, o, a, x, y, d, w, h, support;
image(
pair A, B, C, D, E, o[];
path support;
numeric a, x[], y[], d[], w, h;
x1 := (l**2 + abs(l)*((sqrt(8)*AB)++l))/4AB; % ,
y1 := l+-+x1; %
y2 := m - ((AB-x1)++y1); %
A := (0, 0);
B := (AB*cm, 0);
D := (x1*cm, -y1*cm);
C := D shifted (0, -y2*cm);
d1 := 2/3cm; d2 := 1cm; d3 := 5/6d1; % ,
w := 2/3cm; h := 1/3cm; % . ,
o1 := (unitvector(CD) rotated 90 scaled 1/2d3);
o2 := (unitvector(DB) rotated 90 scaled 1/2d3);
E := whatever [D shifted o1, C shifted o1]
= whatever [D shifted o2, B shifted o2]; % ,
a := angle(AD);
support := A shifted (-w, 0) -- B shifted (w, 0) -- B shifted (w, h) -- A shifted (-w, h) -- cycle;
draw woodenThing(support, 0); % ,
draw pulley (d1, a - 90) shifted E; %
draw image(
draw A -- D -- B withpen thickpen;
draw D -- C withpen thickpen;
) maskedWith (pulleyOutline shifted E); %
draw sphere.c(d2) shifted C shifted (0, -1/2d2); %
dotlabel.llft(btex $A$ etex, A);
dotlabel.lrt(btex $B$ etex, B);
dotlabel.ulft(btex $C$ etex, C);
label.llft(btex $l$ etex, 1/2[A, D]);
)
enddef;
beginfig(18);
draw lHopitalPulley (6, 2, 11/2); % ,
draw lHopitalPulley (3, 5/2, 3) shifted (8cm, 0);
endfig;
O que é um livro didático? Infelizmente, quando quase todas as ilustrações e o layout estavam prontos, algo aconteceu lá e ele nunca saiu. Portanto, provavelmente, algum tempo depois, reescrevi todas as principais coisas da biblioteca resultante novamente e
publiquei o código no github . Alguns kunshtyuki não entraram lá: por exemplo, circuitos elétricos ou uma função para desenhar carros e tratores. Alguns - adicionados: nós, por exemplo.
Toda essa cozinha não funciona rapidamente: leva cerca de um minuto para coletar todas as fotos deste artigo com o LuaLaTeX no meu laptop com o i5-4200U 1.6 GHz. Para muitas coisas, é usado um gerador de números pseudo-aleatórios, para que imagens semelhantes pareçam um pouco diferentes não apenas dentro de uma execução (esse é um recurso), mas cada execução seguinte apresentará imagens diferentes da anterior. Mas você sempre pode definir a
randomseed := - no preâmbulo, e todas as mesmas execuções produzirão as mesmas imagens.