Na verdade, ele é o mais. Mas as primeiras coisas primeiro.
Declaração do problema
Domino python, resolvo tudo no Codewars. Encontro uma tarefa bem conhecida sobre arranha-céus e ovos. A única diferença é que os dados de origem não são 100 andares e 2 ovos, mas um pouco mais.
Dado: N ovos, M tenta jogá-los, arranha-céus sem fim.
Definir: o piso máximo a partir do qual você pode jogar um ovo sem quebrar. Os ovos são esféricos no vácuo e, se um deles não quebrar, caindo, por exemplo, do 99º andar, os outros também suportarão uma queda de todos os andares com menos de um centésimo.
0 <= N, M <= 20.000.
O tempo de execução de duas dezenas de testes é de 12 segundos.
Procure uma solução
Precisamos escrever uma função height (n, m), que retornará o número do piso para o dado n, m. Como ele será mencionado com muita frequência, e toda vez que você escrever preguiça em “altura”, em todos os lugares, exceto no código, eu o designarei como f (n, m).
Vamos começar com zeros. Obviamente, se não houver ovos ou tentativas de jogá-los, nada poderá ser determinado e a resposta será zero.
f (0, m) = 0, f (n, 0) = 0.Suponha que exista um ovo e dez tentativas. Você pode arriscar tudo e jogá-lo imediatamente a partir do centésimo andar, mas, em caso de falha, não poderá determinar mais nada, por isso é mais lógico começar no primeiro andar e subir um andar após cada lançamento, até que a tentativa ou o ovo termine. O máximo que você pode obter se o ovo não falhar é o número 10 do andar.
F (1, m) = mPegue o segundo ovo, tente novamente 10. Agora, então você pode se arriscar com um centésimo? Se quebrar, haverá mais uma e 9 tentativas, pelo menos 9 andares poderão passar. Então talvez você precise arriscar não a partir do centésimo, mas a partir do décimo? É lógico. Então, se for bem-sucedido, restarão 2 ovos e 9 tentativas. Por analogia, agora você precisa subir mais 9 andares. Com uma série de sucessos - outros 8, 7, 6, 5, 4, 3, 2 e 1. No total, estamos no 55º andar com dois ovos inteiros e sem tentar. A resposta é a soma dos primeiros M membros da progressão aritmética com o primeiro membro 1 e a etapa 1.
f (2, m) = (m * m + m) / 2 . Também está claro que em cada etapa a função f (1, m) foi chamada, mas isso ainda não é preciso.
Continue com três ovos e dez tentativas. No caso de um primeiro arremesso malsucedido, os pisos cobertos por 2 ovos e 9 tentativas serão cobertos por baixo, o que significa que o primeiro arremesso deve ser feito do chão f (2, 9) + 1. Então, se for bem-sucedido, temos 3 ovos e 9 tentativas . E para a segunda tentativa, você precisa subir mais f (2.8) + 1 andares. E assim por diante, até 3 ovos e 3 tentativas permanecerem nas mãos. E então é hora de se distrair considerando casos com N = M, quando há tantos óvulos quanto tentativas.
E, ao mesmo tempo, quando há mais ovos.Mas aqui tudo é óbvio - os ovos além daqueles que quebram não serão úteis para nós, mesmo que todo arremesso não tenha êxito. f (n, m) = f (m, m) se n> m . E, no total, 3 ovos, 3 arremessos. Se o primeiro ovo quebrar, você poderá marcar f (2, 2) pisos na parte inferior e, se não quebrar, f (3,2) pisos na parte superior, ou seja, o mesmo f (2, 2). Total f (3, 3) = 2 * f (2, 2) + 1 = 7. E f (4, 4), por analogia, consistirá em dois f (3, 3) e um, e será 15. Todos assemelha-se às potências de dois e escrevemos: f (m, m) = 2 ^ m - 1 .
Parece uma pesquisa binária no mundo físico: começamos do número 2 ^ (m-1); em caso de sucesso, subimos 2 ^ (m-2), e, em caso de falha, diminuímos tanto; até que as tentativas acabem. No nosso caso, aumentamos o tempo todo.
Vamos voltar para f (3, 10). De fato, em cada etapa, ela se resume à soma f (2, m-1) - o número de andares que pode ser determinado em caso de falha, unidades ef (3, m-1) - o número de andares que pode ser determinado em caso de sucesso. E fica claro que, a partir do aumento do número de ovos e tentativas, é improvável que algo mude.
f (n, m) = f (n - 1, m - 1) + 1 + f (n, m - 1) . E essa é uma fórmula universal que pode ser implementada em código.
from functools import lru_cache @lru_cache() def height(n,m): if n==0 or m==0: return 0 elif n==1: return m elif n==2: return (m**2+m)/2 elif n>=m: return 2**n-1 else: return height(n-1,m-1)+1+height(n,m-1)
Obviamente, eu pisei anteriormente em funções recursivas não-memoizantes e descobri que f (10, 40) leva quase 40 segundos com o número de chamadas para si - 97806983. Mas a memoização também salva apenas nos intervalos iniciais. Se f (200.400) for executado em 0,8 segundos, f (200, 500) já estará em 31 segundos. É engraçado que, ao medir o tempo de execução usando% timeit, o resultado é muito menor que o real. Obviamente, a primeira execução da função leva a maior parte do tempo, enquanto o restante simplesmente usa os resultados de sua memorização. Mentiras, mentiras descaradas e estatísticas.
Não é necessária recursão, procuramos mais
Assim, nos testes, por exemplo, aparece f (9477, 10000), mas meu patético f (200, 500) não se encaixa mais no momento certo. Portanto, existe outra solução, sem recursão, continuaremos sua busca. Eu completei o código contando chamadas de função com determinados parâmetros para ver o que ele acabou se decompondo. Por 10 tentativas, foram obtidos os seguintes resultados:
f (3,10) = 7+ 1 * f (2,9) + 1 * f (2,8) + 1 * f (2,7) + 1 * f (2,6) + 1 * f (2) , 5) + 1 * f (2,4) + 1 * f (2,3) + 1 * f (3,3)
f (4,10) = 27+ 1 * f (2,8) + 2 * f (2,7) + 3 * f (2,6) + 4 * f (2,5) + 5 * f (2) , 4) + 6 * f (2,3) + 6 * f (3,3) + 1 * f (4,4)
f (5,10) = 55+ 1 * f (2,7) + 3 * f (2,6) + 6 * f (2,5) + 10 * f (2,4) + 15 * f (2) , 3) + 15 * f (3,3) + 5 * f (4,4) + 1 * f (5,5)
f (6,10) = 69+ 1 * f (2,6) + 4 * f (2,5) + 10 * f (2,4) + 20 * f (2,3) + 20 * f (3) , 3) + 10 * f (4,4) + 4 * f (5,5) + 1 * f (6,6)
f (7,10) = 55+ 1 * f (2,5) + 5 * f (2,4) + 15 * f (2,3) + 15 * f (3,3) + 10 * f (4 , 4) + 6 * f (5,5) + 3 * f (6,6) + 1 * f (7,7)
f (8,10) = 27+ 1 * f (2,4) + 6 * f (2,3) + 6 * f (3,3) + 5 * f (4,4) + 4 * f (5 , 5) + 3 * f (6,6) + 2 * f (7,7) + 1 * f (8,8)
f (9,10) = 7+ 1 * f (2,3) + 1 * f (3,3) + 1 * f (4,4) + 1 * f (5,5) + 1 * f (6 , 6) + 1 * f (7,7) + 1 * f (8,8) + 1 * f (9,9)
Alguma regularidade é visível:

Esses coeficientes são teoricamente calculados. Cada azul é a soma do topo e da esquerda. E os violetas são os mesmos azuis, apenas na ordem inversa. Você pode calcular, mas isso é novamente uma recursão e fiquei decepcionado. Muito provavelmente, muitos (é uma pena que não sou eu) já tenham aprendido esses números, mas por enquanto vou manter a intriga, seguindo minha própria solução. Eu decidi cuspir neles e ir para o outro lado.
Ele abriu o exel, construiu uma placa com os resultados da função e começou a procurar padrões. C3 = SE (C $ 2> $ B3; 2 ^ $ B3-1; C2 + B2 + 1), em que $ 2 é a linha com o número de ovos (1-13), $ B é a coluna com o número de tentativas (1-20), C3 - célula na interseção de dois óvulos e uma tentativa.
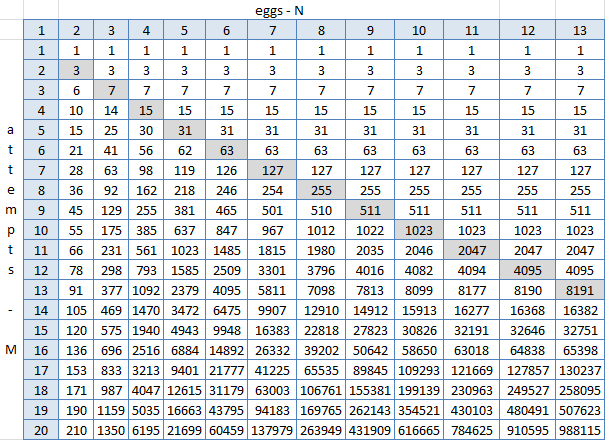
A diagonal cinza é N = M, e aqui é claramente visível que à direita (para N> M) nada muda. Isso pode ser visto - mas não pode ser de outra maneira, porque esses são todos os resultados do trabalho da fórmula, no qual é dado que cada célula é igual à soma da parte superior, superior esquerda e uma. Mas alguma fórmula universal em que você pode substituir N e M e obter o número do andar não foi encontrada. Spoiler: não existe. Mas então, é tão simples criar essa tabela no Excel, talvez seja possível gerar o mesmo python e arrastar respostas dele?
Numpy você não
Lembro que existe o NumPy, que foi projetado apenas para trabalhar com matrizes multidimensionais, por que não tentar? Para começar, precisamos de uma matriz unidimensional de zeros de tamanho N + 1 e de uma matriz unidimensional de unidades de tamanho N. Pegue a primeira matriz de zero ao penúltimo elemento, adicione-a elementwise com a primeira matriz do primeiro elemento ao último e com uma matriz de unidades. Para a matriz resultante, adicione zero ao início. Repita M vezes. O número do elemento N da matriz resultante será a resposta. Os três primeiros passos são assim:
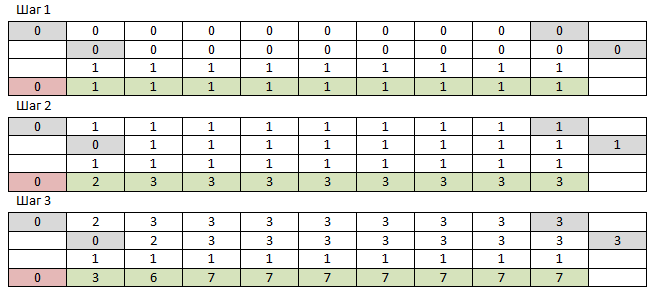
O NumPy funciona tão rápido que não salvei a tabela inteira - toda vez que leio a linha necessária novamente. Uma coisa - o resultado de trabalhar em grandes números estava errado. Classes mais altas são como aquelas, enquanto as mais baixas não são. É assim que os erros aritméticos dos números de ponto flutuante acumulados a partir de múltiplas adições se parecem. Não importa - você pode alterar o tipo da matriz para int. Não, problema - verificou-se que, por uma questão de velocidade, o NumPy funciona apenas com seus tipos de dados, e seu int, diferentemente do Python int, não pode ter mais que 2 ^ 64-1, após o qual transborda silenciosamente e continua com -2 ^ 64. E eu realmente espero números com menos de três mil caracteres. Mas funciona muito rápido, f (9477, 10000) corre 233 ms, acaba sendo uma espécie de absurdo na saída. Eu nem vou dar o código, já que isso. Vou tentar fazer o mesmo um python limpo.
Iterado, iterado, mas não iterado
def height(n, m): arr = [0]*(n+1) while m > 0: arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) m-=1 return arr[n]
44 segundos para calcular f (9477, 10000) é um pouco demais. Mas com certeza. O que pode ser otimizado? Primeiro, não há necessidade de considerar tudo à direita da diagonal M, M. O segundo - considerar a última matriz como um todo, por uma célula. Para isso, as duas últimas duas células da anterior serão ajustadas. Para calcular f (10, 20), apenas essas células cinzas serão suficientes:
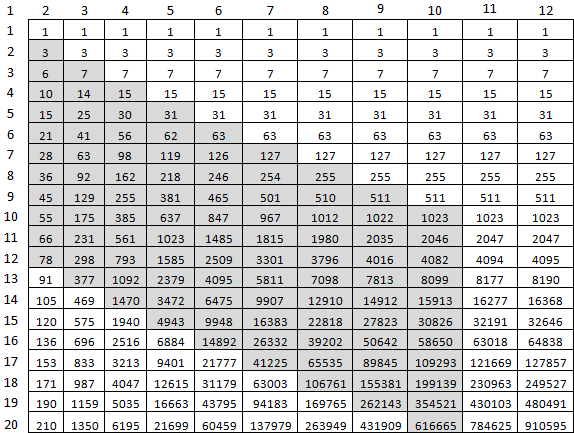
E assim parece no código:
def height(n, m): arr = [0, 1, 1] i = 1 while i < n and i < mn:
E o que você acha? f (9477, 10000) em 2 segundos! Mas essa entrada é muito boa, o comprimento da matriz em qualquer estágio não passará de 533 elementos (10000-9477). Vamos verificar f (5477, 10000) - 11 segundos. Também é bom, mas apenas em comparação com 44 segundos - vinte testes com esse tempo não serão aprovados.
Não é isso. Mas como existe uma tarefa, existe uma solução e a pesquisa continua. Comecei a olhar para a tabela do Excel novamente. A célula à esquerda de (m, m) é sempre uma a menos. E a célula à esquerda dela não está mais lá, em cada linha a diferença se torna maior. A célula abaixo (m, m) é sempre duas vezes maior. E a célula abaixo dela não é mais duas vezes, mas é um pouco menor, mas para cada coluna de maneira diferente, quanto mais longe, maior. E também os números em uma linha no início crescem rapidamente e depois no meio lentamente. Deixe-me criar uma tabela de diferenças entre células vizinhas, talvez que padrão apareça lá?
Mais quente
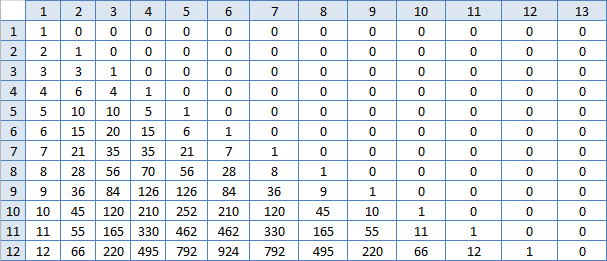
Bah, números familiares! Ou seja, a soma N desses números na linha número M é esta a resposta? É verdade que contá-los é quase o mesmo que eu já fiz, é improvável que isso acelere bastante o trabalho. Mas você tem que tentar:
f (9477, 10000): 17 segundos def height(n, m): arr = [1,1] while m > 1: arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1])) + [1] m-=1 return sum(arr[1:n+1])
Ou 8, se você contar apenas metade do triângulo def height(n, m): arr = [1,1] while m > 2 and len(arr) < n+2:
Para não dizer que uma solução mais ideal. Funciona mais rápido em alguns dados, mais lento em alguns. Nós devemos ir mais fundo. O que é esse triângulo com números que apareceram na solução duas vezes? É uma pena admitir, mas esqueci com segurança a matemática superior, onde o triângulo deve ter figurado, então tive que pesquisar no Google.
Bingo!
Triângulo de Pascal , como é chamado oficialmente. Tabela de coeficiente binomial infinito. Portanto, a resposta para o problema com N ovos e M joga é a soma dos primeiros coeficientes de N na expansão do binômio de Newton do M-grau, exceto o zero.
Um coeficiente binomial arbitrário pode ser calculado através dos fatoriais do número da linha e do número do coeficiente na linha: bk = m! / (N! * (Mn!)). Mas a melhor parte é que você pode calcular seqüencialmente os números na string, sabendo seu número e coeficiente zero (sempre um): bk [n] = bk [n-1] * (m - n + 1) / n. A cada etapa, o numerador diminui em um e o denominador aumenta. E a solução final concisa é assim:
def height(n, m): h, bk = 0, 1
33 ms para o cálculo de f (9477, 10000)! Essa solução também pode ser otimizada, embora nos intervalos fornecidos e funcione bem. Se n estiver na segunda metade do triângulo, podemos invertê-lo para mn, calcular a soma dos primeiros n coeficientes e subtraí-lo de 2 ^ m-2. Se n estiver próximo do meio e m for ímpar, os cálculos também poderão ser reduzidos: a soma da primeira metade da linha será 2 ^ (m-1) -1, o último coeficiente da primeira metade pode ser calculado por meio de fatoriais, seu número é (m-1) / 2 e, em seguida, continue adicionando coeficientes se n estiver na metade direita do triângulo ou subtraindo se estiver à esquerda. Se m for par, não será possível contar a metade da linha, mas você poderá encontrar a soma dos primeiros coeficientes m / 2 + 1 calculando a média por meio de fatoriais e adicionando metade a 2 ^ (m-1) -1. Nos dados de entrada na região de 10 ^ 6, isso reduz notavelmente o tempo de execução.
Após uma decisão bem-sucedida, comecei a procurar a pesquisa de outra pessoa sobre esse assunto, mas encontrei o mesmo nas entrevistas, com apenas dois óvulos, e isso não é esporte. A Internet ficará incompleta sem a minha decisão, decidi, e aqui está.