Este é o último artigo de uma série de artigos de treinamento para desenvolvedores no campo da inteligência artificial. Ele discute as etapas para criar um modelo de aprendizado profundo para gerar música, escolher o modelo certo e o pré-processamento de dados e descreve os procedimentos para definir, treinar, testar e modificar o BachBot.
Geração musical - Pensando em uma tarefa
O primeiro passo para resolver muitos problemas usando inteligência artificial (AI) é reduzir o problema a um problema básico que pode ser resolvido por meio da IA. Um desses problemas é a previsão de sequência, usada em aplicativos de tradução e processamento de idiomas naturais. Nossa tarefa de gerar música pode ser reduzida ao problema de prever uma sequência, e a previsão será executada para uma sequência de notas musicais.
Seleção de modelo
Existem vários tipos diferentes de redes neurais que podem ser consideradas modelos: redes neurais de distribuição direta, redes neurais recorrentes e redes neurais de memória de longo prazo.
Os neurônios são os elementos abstratos básicos que se combinam para formar redes neurais. Essencialmente, um neurônio é uma função que recebe dados na entrada e gera o resultado.
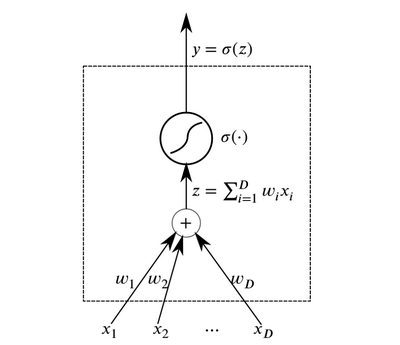NeuronCamadas de neurônios que recebem os mesmos dados na entrada e têm saídas conectadas podem ser combinadas para construir uma
rede neural com propagação direta . Tais redes neurais demonstram altos resultados devido à composição de funções de ativação não lineares ao passar dados através de várias camadas (o chamado aprendizado profundo).
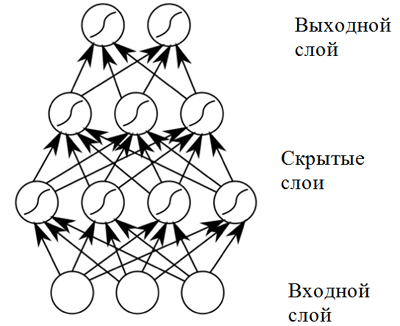Rede neural de distribuição diretaUma rede neural de distribuição direta mostra bons resultados em uma ampla gama de aplicações. No entanto, essa rede neural tem uma desvantagem que não permite que seja usada em uma tarefa relacionada à composição musical (previsão de sequência): possui uma dimensão fixa dos dados de entrada e as composições musicais podem ter comprimentos diferentes. Além disso,
as redes neurais de distribuição direta não levam em consideração a entrada de etapas anteriores, o que as torna pouco úteis para resolver o problema de previsão de sequência! Um modelo chamado
rede neural recorrente é mais adequado para esta tarefa.
As redes neurais recursivas resolvem esses dois problemas introduzindo links entre nós ocultos: nesse caso, na próxima etapa, os nós podem receber informações sobre os dados na etapa anterior.
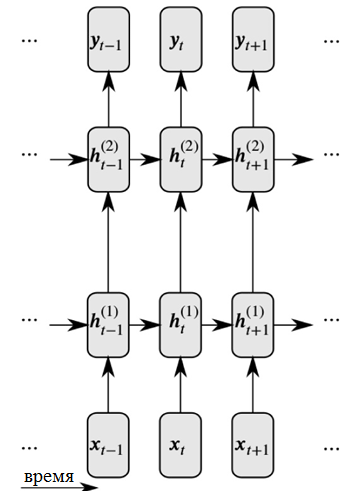Representação detalhada de uma rede neural recorrenteComo você pode ver na figura, cada neurônio agora recebe informações da camada neural anterior e do tempo anterior.
As redes neurais recursivas que lidam com grandes seqüências de entrada encontram o chamado
problema do gradiente de fuga : isso significa que a influência de etapas anteriores desaparece rapidamente. Esse problema é característico da tarefa de composição musical, uma vez que existem importantes dependências de longo prazo nas obras musicais que devem ser levadas em consideração.
Para resolver o problema de um gradiente de fuga
, pode ser usada uma modificação da rede recorrente, chamada
rede neural com memória de longo prazo (ou rede neural LSTM) . Esse problema é resolvido com a introdução de células de memória, que são cuidadosamente monitoradas por três tipos de "portas". Clique no link a seguir para obter mais informações:
Informações gerais sobre redes neurais LSTM .
Assim, o BachBot usa um modelo baseado na rede neural LSTM.
Pré-tratamento
A música é uma forma de arte muito complexa e inclui várias dimensões: tom, ritmo, andamento, tons dinâmicos, articulação e muito mais. Para simplificar a música para os propósitos deste projeto
, apenas o tom e a duração dos sons são considerados . Além disso, todos os corais foram
transpostos para a tecla em Dó maior ou A menor, e as durações das notas foram
quantizadas no tempo (arredondadas) para o múltiplo mais próximo da décima sexta nota. Essas ações foram tomadas para reduzir a complexidade das composições e aumentar o desempenho da rede, enquanto o conteúdo básico da música permaneceu inalterado. Operações para normalizar as tonalidades e durações das notas foram realizadas na biblioteca music21.
def standardize_key(score): """Converts into the key of C major or A minor. Adapted from https://gist.github.com/aldous-rey/68c6c43450517aa47474 """
O código usado para padronizar os caracteres-chave nas obras coletadas, as chaves em Dó maior ou A menor são usadas na saídaA quantização do tempo para o múltiplo mais próximo da décima sexta nota foi realizada usando a função
Stream.quantize () da biblioteca
music21 . A seguir, é apresentada uma comparação das estatísticas associadas a um conjunto de dados antes e após seu processamento preliminar:
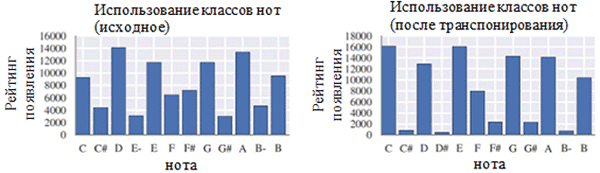Usando cada classe de notas antes (esquerda) e após o pré-processamento (direita). Uma classe de nota é uma nota independentemente da sua oitava.
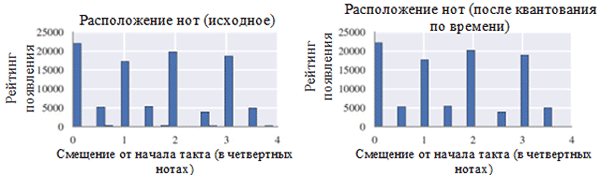Localização das notas antes (esquerda) e após o pré-processamento (direita)Como pode ser visto na figura acima, a transposição da tecla original das corais para a tecla C maior ou C menor (A menor) influenciou significativamente a classe de notas utilizadas nos trabalhos coletados. Em particular, o número de ocorrências de anotações em chaves nas principais (C maior) e A menor (A menor) (C, D, E, F, G, A, B) aumentou. Você também pode observar pequenos picos para as notas F # e G # devido à sua presença na sequência ascendente do A menor melódico (A, B, C, D, E, F # e G #).
Por outro lado, a quantização do tempo teve um efeito muito menor. Isso pode ser explicado pela alta resolução da quantização (semelhante ao arredondamento para muitos dígitos significativos).
Codificação
Após o pré-processamento dos dados, é necessário codificar as corais em um formato que possa ser facilmente processado usando uma rede neural recorrente. O formato necessário é uma
sequência de tokens . Para o projeto BachBot, a codificação foi escolhida no nível das notas (cada token representa uma nota) em vez do nível dos acordes (cada token representa um acorde). Esta solução reduziu o tamanho do dicionário de 128
4 acordes possíveis para 128 notas possíveis, o que permitiu aumentar a eficiência do trabalho.
Um esquema de codificação original para composições musicais foi criado para o projeto BachBot. O coral é dividido em etapas de tempo correspondentes a semicolcheias. Essas etapas são chamadas de quadros. Cada quadro contém uma sequência de tuplas representando o valor da afinação de uma nota no formato de uma interface de instrumento musical digital (MIDI) e um sinal de ligação desta nota a uma nota anterior da mesma altura (nota, sinal de ligação). As notas no quadro são numeradas em ordem decrescente de altura (soprano → alt → tenor → baixo). Cada quadro também pode ter um quadro que marca o final de uma frase; Fermata é representado por um símbolo de ponto (.) Acima da nota. Os símbolos
INÍCIO e
FIM são adicionados ao início e ao final de cada coral. Esses símbolos causam a inicialização do modelo e permitem ao usuário determinar quando a composição termina.
START
(59, True)
(56, True)
(52, True)
(47, True)
|||
(59, True)
(56, True)
(52, True)
(47, True)
|||
(.)
(57, False)
(52, False)
(48, False)
(45, False)
|||
(.)
(57, True)
(52, True)
(48, True)
(45, True)
|||
ENDUm exemplo de codificação de dois acordes. Cada acorde dura uma oitava batida de uma medida, o segundo acorde é acompanhado por uma fazenda. A sequência "|||" marca o fim do quadro def encode_score(score, keep_fermatas=True, parts_to_mask=[]): """ Encodes a music21 score into a List of chords, where each chord is represented with a (Fermata :: Bool, List[(Note :: Integer, Tie :: Bool)]). If `keep_fermatas` is True, all `has_fermata`s will be False. All tokens from parts in `parts_to_mask` will have output tokens `BLANK_MASK_TXT`. Time is discretized such that each crotchet occupies `FRAMES_PER_CROTCHET` frames. """ encoded_score = [] for chord in (score .quantize((FRAMES_PER_CROTCHET,)) .chordify(addPartIdAsGroup=bool(parts_to_mask)) .flat .notesAndRests):
Código usado para codificar a tonalidade music21 usando um esquema de codificação especialTarefa de modelo
Na parte anterior, foi dada uma explicação mostrando que a tarefa de composição automática pode ser reduzida à tarefa de prever uma sequência. Em particular, um modelo pode prever a próxima nota mais provável com base nas notas anteriores. Para resolver esse tipo de problema, uma rede neural com memória de longo prazo (LSTM) é mais adequada. Formalmente, o modelo deve prever P (x
t + 1 | x
t , h
t-1 ), a distribuição de probabilidade para as próximas notas possíveis (x
t + 1 ) com base no token atual (x
t ) e no estado oculto anterior (h
t-1 ) . Curiosamente, a mesma operação é realizada por modelos de linguagem baseados em redes neurais recorrentes.
No modo de composição, o modelo é inicializado com o token
START , após o qual seleciona o próximo token mais provável a seguir. Depois disso, o modelo continua a selecionar o próximo token mais provável usando a nota anterior e o estado oculto anterior até que um token END seja gerado. O sistema contém elementos de temperatura que adicionam algum grau de aleatoriedade para impedir que o BachBot componha a mesma peça repetidamente.
Função de perda
Ao treinar um modelo para previsão, geralmente há alguma função que precisa ser minimizada (chamada de função de perda). Esta função descreve a diferença entre a previsão do modelo e a propriedade de verdade básica. O BachBot minimiza a perda de entropia cruzada entre a distribuição prevista (x
t + 1 ) e a distribuição real da função objetivo. Usar entropia cruzada como uma função de perda é um bom ponto de partida para uma ampla gama de tarefas, mas em alguns casos você pode usar sua própria função de perda. Outra abordagem aceitável é tentar usar várias funções de perda e aplicar um modelo que minimize a perda real durante a verificação.
Treinamento / teste
Ao treinar uma rede neural recursiva, o BachBot usou a correção de token com o valor x
t + 1 em vez de aplicar a previsão do modelo. Esse processo, conhecido como aprendizado obrigatório, é usado para garantir a convergência, pois as previsões do modelo produzirão naturalmente maus resultados no início do treinamento. Por outro lado, durante a validação e composição, a previsão do modelo x
t + 1 deve ser reutilizada como entrada para a próxima previsão.
Outras considerações
Para aumentar a eficiência desse modelo, foram utilizados os seguintes métodos práticos comuns às redes neurais LSTM: truncamento de gradiente normalizado, método de eliminação, normalização de pacotes e método de propagação de erro de tempo truncado (BPTT).
O método de truncamento de gradiente normalizado elimina o problema do crescimento descontrolado do valor do gradiente (o inverso do problema de gradiente de fuga, que foi resolvido usando a arquitetura das células de memória LSTM). Usando essa técnica, os valores de gradiente que excedem um determinado limite são truncados ou redimensionados.
O método de exclusão é uma técnica na qual alguns neurônios
selecionados aleatoriamente são desconectados (excluídos) durante o treinamento em rede. Isso evita o ajuste excessivo e melhora a qualidade da generalização. O problema do ajuste excessivo surge quando o modelo é otimizado para o conjunto de dados de treinamento e, em menor grau, aplicável a amostras fora deste conjunto. O método de exclusão geralmente piora a perda durante o treinamento, mas a melhora na fase de verificação (mais sobre isso abaixo).
O cálculo do gradiente em uma rede neural recorrente para uma sequência de 1000 elementos é equivalente em custo às passagens para frente e para trás na rede neural de distribuição direta de 1000 camadas.
O método de
propagação de retorno de erro truncado (BPTT) ao longo do tempo é usado para reduzir o custo da atualização de parâmetros durante o treinamento. Isso significa que os erros são propagados apenas durante um número fixo de etapas contadas a partir do momento atual. Observe que as dependências de aprendizado de longo prazo ainda são possíveis com o método BPTT, pois os estados latentes já foram revelados em várias etapas anteriores.
Parâmetros
A seguir, é apresentada uma lista de parâmetros relevantes para modelos de redes neurais recorrentes / redes neurais com memória de curto prazo longa:
- O número de camadas . Aumentar esse parâmetro pode aumentar a eficiência do modelo, mas levará mais tempo para treiná-lo. Além disso, muitas camadas podem levar ao sobreajuste.
- A dimensão do estado latente . Aumentar esse parâmetro pode aumentar a complexidade do modelo, no entanto, isso pode levar ao sobreajuste.
- Dimensão das comparações de vetores
- O comprimento da sequência / número de quadros antes de truncar a propagação de retorno do erro ao longo do tempo.
- Probabilidade de exclusão de neurônios . A probabilidade com que um neurônio será excluído da rede durante cada ciclo de atualização.
A metodologia para selecionar o conjunto ideal de parâmetros será discutida mais adiante neste artigo.
Implementação, treinamento e testes
Seleção de plataforma
Atualmente, existem muitas plataformas que permitem implementar modelos de aprendizado de máquina em várias linguagens de programação (incluindo até o JavaScript!). As plataformas populares incluem o
scikit-learn , o
TensorFlow e o
Torch .
A biblioteca do Torch foi selecionada como plataforma para o projeto BachBot. No início, a biblioteca TensorFlow foi testada, mas, na época, utilizava extensas redes neurais recorrentes, o que levou a um excesso de memória RAM da GPU. Torch é uma plataforma de computação científica alimentada pela linguagem de programação rápida LuaJIT *. A plataforma Torch contém excelentes bibliotecas para trabalhar com redes neurais e otimização.
Implementação e treinamento de modelos
A implementação, obviamente, variará dependendo do idioma e da plataforma em que você escolher. Para aprender como o BachBot implementa redes neurais com memória de longo prazo usando Torch, confira os scripts usados para treinar e definir os parâmetros do BachBot. Esses scripts estão disponíveis no site do
Feynman Lyang GitHub.Um bom ponto de partida para navegar no repositório é o
script 1-train.zsh . Com ele, você pode encontrar o caminho para o arquivo
bachbot.py .
Mais precisamente, o script principal para definir os parâmetros do modelo é o arquivo
LSTM.lua . O script para treinar o modelo é o arquivo
train.lua .
Otimização de hiperparâmetros
Para pesquisar os valores ótimos dos hiperparâmetros, o método de pesquisa em grade foi usado usando a seguinte grade de parâmetros.
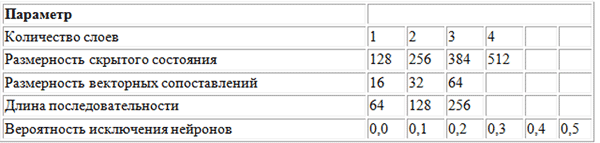Grade de parâmetros usados pelo BachBot na pesquisa de gradeUma pesquisa em grade é uma pesquisa completa de todas as combinações possíveis de parâmetros. Outros métodos sugeridos para otimizar os hiperparâmetros são a pesquisa aleatória e a otimização bayesiana.
O conjunto ideal de hiperparâmetros detectados como resultado de uma pesquisa em grade é o seguinte: número de camadas = 3, dimensão do estado oculto = 256, dimensão das comparações de vetores = 32, comprimento da sequência = 128, probabilidade de eliminação de neurônios = 0,3.
Esse modelo atingiu uma perda de entropia cruzada de 0,324 durante o treinamento e 0,477 na etapa de verificação. O gráfico da curva de aprendizado demonstra que o processo de aprendizado converge após 30 iterações (± 28,5 minutos ao usar uma única GPU).
Os gráficos de perda durante o treinamento e durante a fase de verificação também podem ilustrar o efeito de cada hiperparâmetro. De particular interesse para nós é a probabilidade de eliminar neurônios:
Curvas de aprendizado para várias configurações do método de exclusãoPode ser visto na figura que o método de eliminação realmente evita a ocorrência de sobreajuste. Embora com uma probabilidade de exclusão de 0,0, a perda durante o treinamento seja mínima, no estágio de verificação, a perda tem um valor máximo. Grandes valores de probabilidade levam a um aumento nas perdas durante o treinamento e a uma diminuição nas perdas no estágio de verificação. O valor mínimo da perda durante a fase de verificação ao trabalhar com o BachBot foi corrigido com uma probabilidade de exceção de 0,3.
Métodos de avaliação alternativos (opcional)
Para alguns modelos - especialmente para aplicativos criativos, como compor músicas -, a perda pode não ser uma medida apropriada do sucesso do sistema. Em vez disso, a percepção humana subjetiva pode ser o melhor critério.
O objetivo do projeto BachBot é compor automaticamente músicas indistinguíveis das próprias composições de Bach. Para avaliar o sucesso dos resultados, foi realizada uma pesquisa com usuários na Internet. A pesquisa recebeu a forma de uma competição na qual os usuários foram solicitados a determinar quais obras pertencem ao projeto BachBot e quais ao Bach.
Os resultados da pesquisa mostraram que os participantes da pesquisa (759 pessoas com diferentes níveis de treinamento) foram capazes de distinguir com precisão entre duas amostras em apenas 59% dos casos. Isso é apenas 9% maior que o resultado de adivinhações aleatórias! Experimente você mesmo a
pesquisa do
BachBot !
Adaptação do modelo à harmonização
Agora, o BachBot pode calcular P (x
t + 1 | x
t , h
t-1 ), a distribuição de probabilidade para as próximas notas possíveis com base na nota atual e no estado oculto anterior. Esse modelo de previsão seqüencial pode ser posteriormente adaptado para harmonizar a melodia. Esse modelo adaptado é necessário para harmonizar a melodia, modulada com a ajuda de emoções, como parte de um projeto musical com uma exibição de slides.
Ao trabalhar com a harmonização de modelos, é fornecida uma melodia predefinida (geralmente essa é uma parte de soprano) e, depois disso, o modelo deve compor músicas para o restante das peças. Para realizar essa tarefa, uma pesquisa gananciosa do “melhor primeiro” é usada com a restrição de que as notas da melodia sejam corrigidas. Os algoritmos gananciosos envolvem decisões ideais do ponto de vista local. Então, abaixo está uma estratégia simples usada para harmonização:
Suponha que x t são tokens na harmonização proposta. No passo t, se a nota corresponde à melodia, então x t é igual à nota fornecida. Caso contrário, x t é igual à próxima nota mais provável, de acordo com as previsões do modelo. O código para essa adaptação de modelo pode ser encontrado no site do Feynman Lyang GitHub: HarmModel.lua , harmonize.lua .
A seguir, é apresentado um exemplo de harmonização da canção de ninar Twinkle, Twinkle, Little Star com o BachBot, usando a estratégia acima.
Harmonização da canção de ninar de Twinkle, Twinkle, Little Star com BachBot (na parte soprano). Partes de viola, tenor e baixo também foram preenchidas com BachBotNeste exemplo, a melodia da canção de ninar Twinkle, Twinkle, Little Star é apresentada na parte soprano. Depois disso, as partes da viola, tenor e baixo foram preenchidas usando o BachBot, usando uma estratégia de harmonização. E
aqui está como isso soa .
Apesar do BachBot mostrar um bom desempenho ao executar esta tarefa, existem certas limitações associadas a este modelo. Mais precisamente, o algoritmo
não aguarda a melodia e usa apenas a nota atual da melodia e o contexto passado para gerar notas subsequentes. Ao harmonizar uma melodia pelas pessoas, elas podem abranger toda a melodia, o que simplifica a derivação de harmonizações adequadas. O fato de esse modelo não ser capaz de fazer isso pode causar
surpresas devido a restrições no uso de informações subsequentes que causam erros. Para resolver esse problema, a chamada
busca por feixe pode ser usada.
Ao usar a busca por feixe, várias linhas de movimento são verificadas. Por exemplo, em vez de usar apenas uma, a nota mais provável que está sendo executada atualmente, quatro ou cinco notas mais prováveis podem ser consideradas, após as quais o algoritmo continua seu trabalho com cada uma dessas notas. Examinar as várias opções pode ajudar o modelo a se
recuperar de erros . A pesquisa por feixe é comumente usada em aplicativos de processamento de linguagem natural para criar sentenças.
As melodias moduladas com a ajuda das emoções agora podem ser passadas por esse modelo de harmonização para completá-las.