Julia. Conhecimento

Ode para Julia

É muito difícil transmitir todo o entusiasmo que acompanhou o lançamento dos primeiros programas e a correção dos primeiros erros usando essa linguagem. É simples e bonito como Python , um pouco como Fortran , trabalho conveniente com matrizes e gráficos, além da capacidade de executar otimização e paralelização feroz, mesmo para manequins como eu meus colegas de classe. Você pode trabalhar em diferentes níveis de abstração: da programação de alto nível com digitação dinâmica, você pode ir até os comandos do assembler, ou seja, aqui você tem acessibilidade do Python e velocidade de execução dos contadores do Fortran. Não consigo me livrar da sensação de que Mathcad , Scilab e até, Deus me perdoe, C ++ estão começando a desbotar em meu coração.

Aprendi sobre o idioma encontrando acidentalmente uma publicação khabroviana e, como um aluno impressionável deveria, comecei a procurar orientação, de preferência em russo. Como a linguagem está em constante evolução há seis anos, as fontes de informação já escassas se tornaram obsoletas e a empolgação começou a diminuir. Porém, com o início de um novo curso de laboratório sobre modelagem de fenômenos físicos, com a livre escolha de uma linguagem de programação, ainda havia uma motivação para começar a conhecer Julia. Além disso, em agosto, o idioma "add up 1.0" .

O material apresentado abaixo foi planejado como uma introdução ao idioma em que todos os trabalhos de laboratório foram escritos e um manual de treinamento foi coletado.

Julia é uma linguagem de programação de digitação dinâmica de alto nível e alto desempenho para cálculos matemáticos. A sintaxe é semelhante à família matlab, a linguagem é escrita em C , C ++ e Scheme , é possível chamar bibliotecas Sysh

Instalação

Bem, tudo finalmente se acalmou, agora à nossa disposição:

• Prompt de comando do JuliaPRO - todas as habilidades de Yulina diretamente do intérprete.
• Juno é um IDE bonito, com uma janela para gráficos e um espaço de trabalho onde você pode ver o conteúdo de todos os objetos
• Jupyter - inicia o núcleo de computação no console e você pode executar o código diretamente no navegador. (Além de Julia, Python também está presente)

Vamos ver o que esta calculadora pode fazer ... Suporte Unicode - você pode usar o alfabeto cirílico, hieróglifos e chamar pi da letra grega. E você não pode especificar explicitamente a multiplicação entre o número e a variável (nessa ordem e sem espaço):

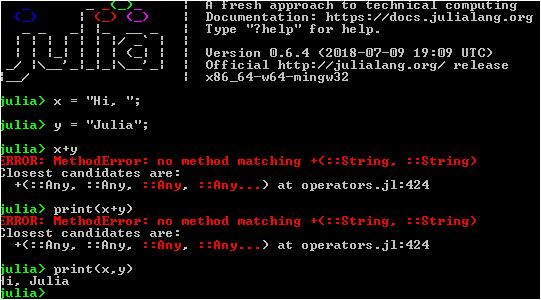
x = 5+8 2x - 3x + 2x^2 Out: 325 

Todos os sinais necessários também estão em vigor: + =, * =, >> =, etc. (O sinal ">>" (deslocamento de bits para a direita). Sinais de comparação:>,> =, <, <=, == ,! =. Desigualdades podem ser combinadas em cadeias:

 y = 5 y += 2 4 <= y < 8 Out: true 

Números complexos disponíveis:

 (2-1im)*(4+3im) Out: 11 + 2im 

E funções para trabalhar com eles:

• real (z) é a parte real,
• imag (z) é a parte imaginária,
• conj (z) é o conjugado complexo,
• abs (z) - módulo
• abs2 (z) é o quadrado do módulo,
• ângulo (z) é o argumento de um número complexo.

Você pode usar números racionais usando "//" e as funções correspondentes:

• num (x) - numerador,
• den (x) - denominador,
• float (x) - converte em decimal

 x = 4//6+5//7 Out: 29//21 float(x) Out: 1.380952380952381 

Julia tem a capacidade de controlar a representação interna de dados:

• typeof (obj) - tipo de objeto
• typemax (obj) é o número máximo desse tipo
• typemin (obj) - mínimo
• eps () - máquina zero
• BigInt é um grande todo
• BigFloat - grande ponto flutuante

 q = 3 typemax(q) Out: 9223372036854775807 typeof(q) Out: Int64 BigFloat(2.3^45/6) Out: 3.159376405019356000000000000000000000000000000000000000000000000000000000000e+15 

Funções

Kit de Recursos

• abs (x) é o módulo de um número,
• abs2 (x) é o quadrado do módulo,
• sqrt (x) é a raiz quadrada,
• cbrt (x) é a raiz cúbica,
• exp (x) é o expoente do número,
• log (x) é o logaritmo natural,
• log10 (x) - logaritmo decimal,
• log (b, x) é o logaritmo de x na base b.
  Assim como trigonométrico, hiperbólico, Airy, Bessel e muitos outros.

Funções personalizadas:

 function () #  end 

A função retorna o resultado da última expressão (usuário do Mathcad soluço).

 function cube(x) x^3 end cube(4) Out: 64 

Bem, ou indicamos explicitamente:

 function myabs(x) if x>=0 return x else return -x end end myabs(-12) Out: 12 

Os valores retornados podem ser coletados em uma tupla:

 function cubeandsquare(x) x^3,x^2 end a,b = cubeandsquare(3) print("a = $a, b = $b") Out: a = 27, b = 9 

As funções podem levar tuplas, valores padrão, palavras-chave. Se não houver colchetes após o nome da função, ela será considerada uma variável e poderá ser atribuída a outra variável ou transferida para a função como parâmetro. Julia também suporta um estilo funcional de escrever programas (Olá Lisp)

 function mysin(t;A=1,?=1,?=0) #   -     A*sin(?*t + ?) end x1 = mysin(pi) #   = 0 x2 = mysin(pi*0.5,A = 2) #      x3 = mysin(pi*0.5,? = 0.5) #      print("x1 = $x1, x2 = $x2, x3 = $x3") Out: x1 = 1.2246467991473532e-16, x2 = 2.0, x3 = 0.7071067811865475 

Matrizes

Como usuário do Scilab , eu nem percebi a substituição: você pode especificar um array usando a função:

• Matriz {T} (undef, dims ...) - Uma matriz do tipo T e dimensão dims
• zeros (T, dims ...) - Matriz de zeros
• ones (T, dims ...) - ou unidades
  A indexação começa com um , em vez de $ - end , e todas as operações necessárias para matrizes são definidas (para executar, por exemplo, adição ou multiplicação por elementos, é necessário colocar um ponto na frente do operador).

(Agora está claro como inserir imagens, mas tudo bem ...)

Funções básicas:

• det (A) - calcula determinante
• A ' - transpõe a matriz
• inv (A) - matriz invertida
• length (A) - número de elementos
• ndims (A) - número de dimensões
• tamanho (A) - tupla de dimensões
• tamanho (A, n) - dimensão em uma determinada direção
• copy (A) - cria uma cópia da matriz
• espaço interno (início, fim, etapa) ou
  linspace (start: step: end) - cria uma matriz unidimensional

 A = [1 2 3; 6 5 4; 7 8 9] Out: 3?3 Array{Int64,2}: 1 2 3 6 5 4 7 8 9 A[2,1] Out: 6 A[end] Out: 9 size(A) Out: (3, 3) 

Você pode selecionar partes da matriz especificando um intervalo de índices ao longo da dimensão com o sinal ":".

 m1 = rand(3,2) m2 = reshape(1:2:11, 3,2) Out: 3?2 Base.ReshapedArray{Int64,2,StepRange{Int64,Int64},Tuple{}}: 1 7 3 9 5 11 m3 = [m1 m2] #   (  ) Out: 3?4 Array{Float64,2}: 0.325649 0.701038 1.0 7.0 0.513579 0.620215 3.0 9.0 0.815242 0.805307 5.0 11.0 m5 = [m1; m2] #   (  ) Out: 6?2 Array{Float64,2}: 0.325649 0.701038 0.513579 0.620215 0.815242 0.805307 1.0 7.0 3.0 9.0 5.0 11.0 m3[:, 2:4] Out: 3?3 Array{Float64,2}: 0.701038 1.0 7.0 0.620215 3.0 9.0 0.805307 5.0 11.0 

Aqui usamos rand (), que retorna uma matriz de números aleatórios de uma determinada dimensão, e reformular (), que altera a dimensão da matriz para a especificada.

 for a in A #   a   A end 

ou

 for i in eachindex(A) #     i end 

ou

 for i = 1 : size(A,n) # n -      (..    ) #     i end 

Gráficos

Para usar gráficos, você precisa baixar um pacote do repositório para escolher:

• Pkg.add ("Gráficos")
• Pkg.add ("PyPlot")
• Pkg.add ("Gadfly")
• Pkg.add ("Winston")

Destes, o mais popular é o PyPlot Pythonic . Os módulos são conectados usando o comando, por exemplo:

 using PyPlot 

No entanto, vamos tentar o Gaston usando o Gnuplot (balanço separadamente).
Carregado pela equipe Gaston.jl

  Pkg.add("Gaston") 

E direto ao ponto:

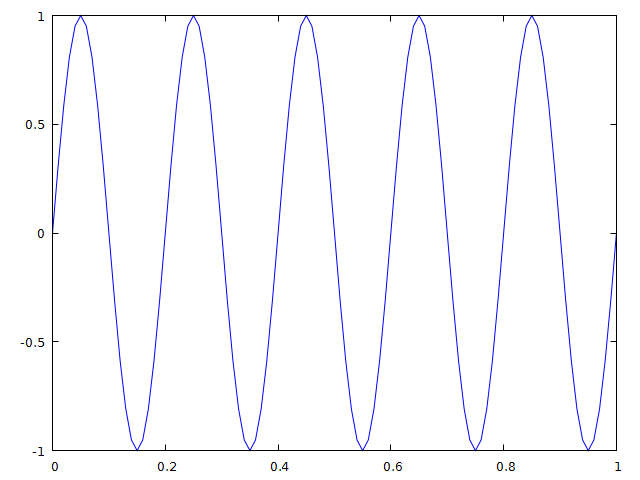
 using Gaston t = 0:0.01:1 plot(t, sin.(2?*5*t)) 

 plot(t,sin.(2?*5*t),title="A sine wave",xlabel="Time (s)",ylabel="Amplitude",grid="on",linewidth=3,color="blue", yrange="[-1.1:1.1]",marker="ecircle",plotstyle="linespoints",linestyle="-.-") 

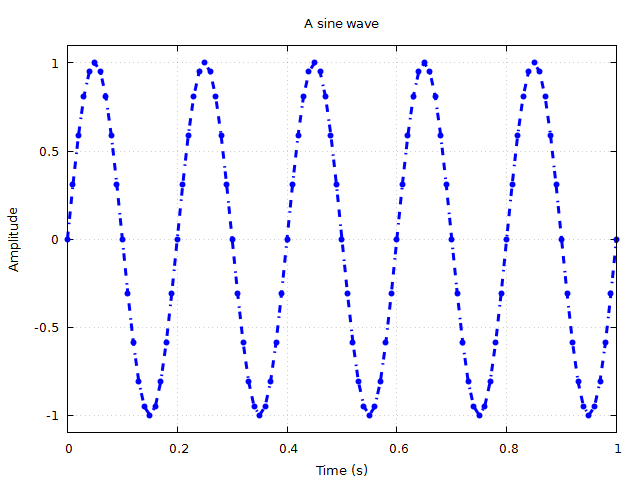
 plot!(t,cos.(2?*5*t),color="red",linewidth=2) #       

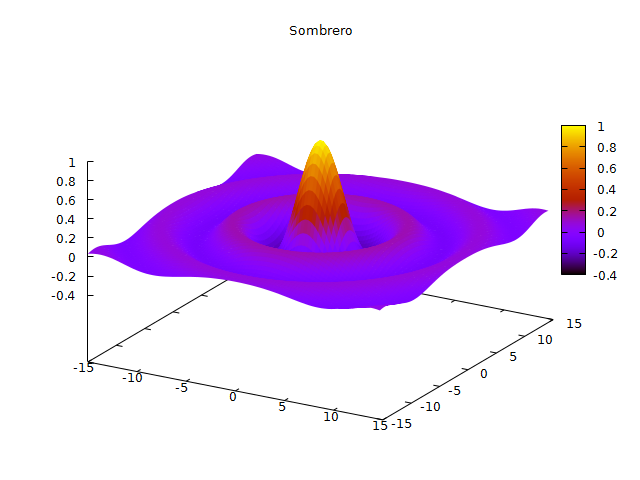
 x = y = -15:0.33:15 surf(x,y,(x,y)->sin.(sqrt.(x.*x+y.*y))./sqrt.(x.*x+y.*y),title="Sombrero",plotstyle="pm3d") 

 x = y = -15:0.33:15 surf(x,y,(x,y)->sin.(sqrt(x.*x+y.*y))./sqrt.(x.*x+y.*y), title="Edge view of a sombrero",plotstyle="pm3d",gpcom="set view 80,20") 

 R = [ x+y for x=0:5:120, y=0:5:120] G = [ x+y for x=0:5:120, y=120:-5:0] B = [ x+y for x=120:-5:0, y=0:5:120] Z = zeros(25,25,3) Z[:,:,1] = R Z[:,:,2] = G Z[:,:,3] = B imagesc(Z,title="RGB Image",clim=[10 200]) 

 histogram(rand(1000),bins=15,norm=1,title="Histogram",yrange="[0:1.6]") 

 y = 1:40 err = Gaston.ErrorCoords(rand(40)) plot(y,err=err,title="Example of error bars",plotstyle="errorbars") 

Você pode criar várias janelas gráficas (não funciona no Jupyter ) usando o comando h = figure () (basta inserir entre plotes). Para salvar o gráfico como um arquivo de imagem, use os comandos
set_filename ("name.png") # se não for especificado, será exibido
printfigure ("png") # salva em arquivo, PNG, PDF, SVG e GIF disponíveis
Mais informações sobre os pacotes Gaston

Conclusão

Existem muitos outros pacotes gráficos para todos os gostos e que cobrem quase todas as necessidades. Além disso, pacotes auxiliares estão sendo desenvolvidos com poder e principal. Aqui você tem computação quântica, bioinformática e aprendizado de máquina, além de muitos outros problemas prementes, como diferenciais e derivados .

Em geral, Julia é linda, inteligente e muito promissora, e é extremamente inadmissível deixá-la sem a devida atenção.