Este artigo discute as semelhanças e diferenças entre as duas abordagens para resolver problemas algorítmicos:
programação dinâmica (programação dinâmica) e o princípio de
“dividir e conquistar” (dividir e conquistar). Vamos comparar usando dois algoritmos como exemplo:
pesquisa binária (como encontrar rapidamente um número em uma matriz classificada) e
distância de Levenshtein (como converter uma linha em outra com um número mínimo de operações).
Quero observar imediatamente que essa comparação e explicação não afirmam ser extremamente corretas. E talvez até alguns professores universitários gostariam de me expulsar :) Este artigo é apenas minha tentativa pessoal de resolver as coisas e entender o que é programação dinâmica e como o princípio de “dividir e conquistar” está envolvido.Então, vamos começar ...
O problema
Quando
comecei a estudar algoritmos, era difícil
para mim entender a idéia básica da programação dinâmica (doravante
DP , da Programação Dinâmica) e como ela difere da abordagem de “dividir e conquistar” (
DC adicional, de dividir e conquistar). Quando se trata de comparar esses dois paradigmas, geralmente
muitos usam com sucesso a função Fibonacci para ilustrar. E esta é uma ótima ilustração. Mas parece-me que, quando usamos
a mesma tarefa para ilustrar DP e DC, perdemos um detalhe importante que pode nos ajudar a perceber a diferença entre as duas abordagens mais rapidamente. E esse detalhe é que essas duas técnicas se manifestam melhor na solução de
diferentes tipos de problemas.
Ainda estou aprendendo DP e DC e não posso dizer que entendi completamente esses conceitos. Mas ainda espero que este artigo lance mais luz e ajude a dar o próximo passo no estudo de abordagens significativas, como programação dinâmica e divisão e conquista.
Semelhanças entre DP e DC
Da maneira como vejo esses dois conceitos agora, posso concluir que o
DP é uma versão estendida do DC .
Eu
não os consideraria algo completamente diferente. Como esses dois conceitos
dividem recursivamente um problema em dois ou mais subproblemas do mesmo tipo até que esses subproblemas sejam fáceis o suficiente para serem resolvidos diretamente. Além disso, todas as soluções para o subproblema são combinadas para, finalmente, dar uma resposta ao problema original.
Então, por que ainda temos duas abordagens diferentes (DP e DC) e por que chamei a programação dinâmica de extensão. Isso ocorre porque a programação dinâmica pode ser aplicada a tarefas que possuem certas
características e limitações . E somente neste caso o DP expande a CD por meio de duas técnicas:
memorização e
tabulação .
Vamos nos aprofundar um pouco mais nos detalhes ...
Limitações e características necessárias para programação dinâmica
Como acabamos de descobrir, existem duas características principais que uma tarefa / problema deve ter para tentar resolvê-lo usando a programação dinâmica:
- Subestrutura ideal - deve ser possível compor uma solução ideal para um problema, de uma solução ideal para suas subtarefas.
- Intersecção de subproblemas - o problema deve ser dividido em subproblemas, que por sua vez são reutilizados repetidamente. Em outras palavras, uma abordagem recursiva para resolver o problema implicaria uma solução múltipla (e não única) para o mesmo subproblema, em vez de produzir subproblemas novos e exclusivos em cada ciclo recursivo.
Assim que encontrarmos essas duas características no problema que estamos considerando, podemos dizer que ele pode ser resolvido usando programação dinâmica.
Programação dinâmica como uma extensão do princípio de "dividir e conquistar"
O DP estende o CD com a ajuda de duas técnicas (
memorização e
tabulação ), cujo objetivo é salvar soluções em subproblemas para sua reutilização futura. Assim, as soluções são armazenadas em cache por subproblemas, o que leva a uma melhoria significativa no desempenho do algoritmo. Por exemplo, a complexidade de tempo de uma implementação recursiva "ingênua" da função Fibonacci é
O(2 n ) . Ao mesmo tempo, uma solução baseada em programação dinâmica é executada em apenas
(n) .
A memorização (preenchendo o cache de cima para baixo) é uma técnica de armazenamento em cache que utiliza soluções recém-computadas para subtarefas. A função Fibonacci usando a técnica de memorização ficaria assim:
memFib(n) { if (mem[n] is undefined) if (n < 2) result = n else result = memFib(n-2) + memFib(n-1) mem[n] = result return mem[n] }
A tabulação (preenchendo o cache de baixo para cima) é uma técnica semelhante, mas que se concentra principalmente no preenchimento do cache, e não em encontrar uma solução para o subproblema. O cálculo dos valores que precisam ser armazenados em cache é, neste caso, mais fácil de ser executado iterativamente, em vez de recursivamente. A função Fibonacci usando a técnica de tabulação ficaria assim:
tabFib(n) { mem[0] = 0 mem[1] = 1 for i = 2...n mem[i] = mem[i-2] + mem[i-1] return mem[n] }
Você pode ler mais sobre a comparação de memorização e tabulação
aqui .
A idéia principal que precisa ser capturada nesses exemplos é que, como nossos problemas de CD têm subproblemas sobrepostos, podemos usar o cache de soluções para subproblemas usando uma das duas técnicas de armazenamento em cache: memorização e tabulação.
Então, qual é a diferença entre DP e DC no final
Aprendemos sobre as limitações e pré-requisitos para o uso de programação dinâmica, bem como as técnicas de armazenamento em cache usadas na abordagem de DP. Vamos tentar resumir e descrever os pensamentos acima na ilustração a seguir:
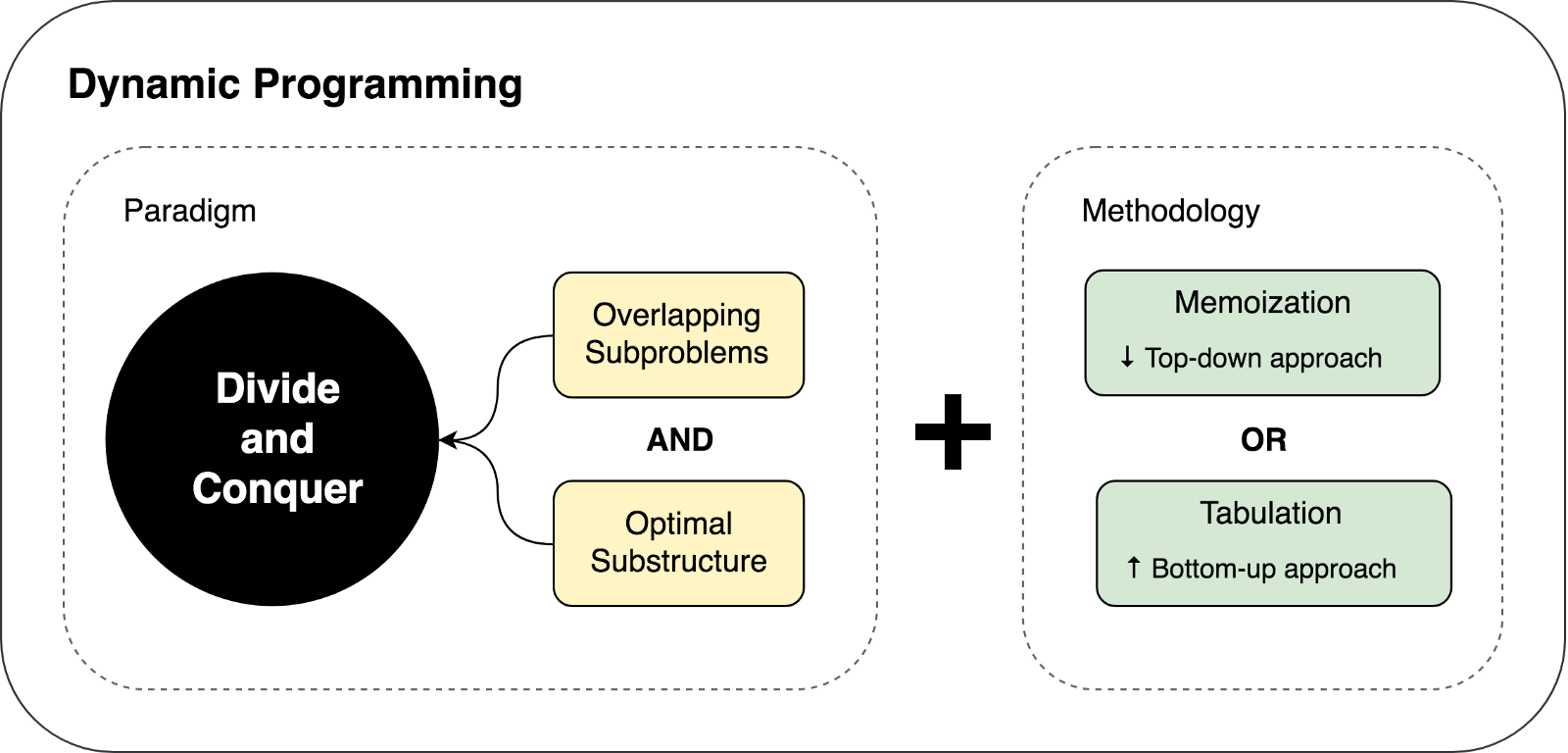
Vamos tentar resolver alguns problemas usando DP e DC para demonstrar essas duas abordagens em ação.
Exemplo de divisão e conquista: Pesquisa binária
O algoritmo de pesquisa
binária é um algoritmo de pesquisa que localiza a posição do elemento solicitado em uma matriz classificada. Na pesquisa binária, comparamos o valor da variável com o valor do elemento no meio da matriz. Se eles não forem iguais, então metade da matriz na qual o elemento desejado não pode ser excluído de pesquisas adicionais. A pesquisa continua nessa metade da matriz, na qual a variável desejada pode ser localizada até ser encontrada. Se a próxima metade da matriz não contiver elementos, a pesquisa será considerada completa e concluímos que a matriz não contém o valor desejado.
ExemploA ilustração abaixo é um exemplo de uma pesquisa binária para o número 4 em uma matriz.
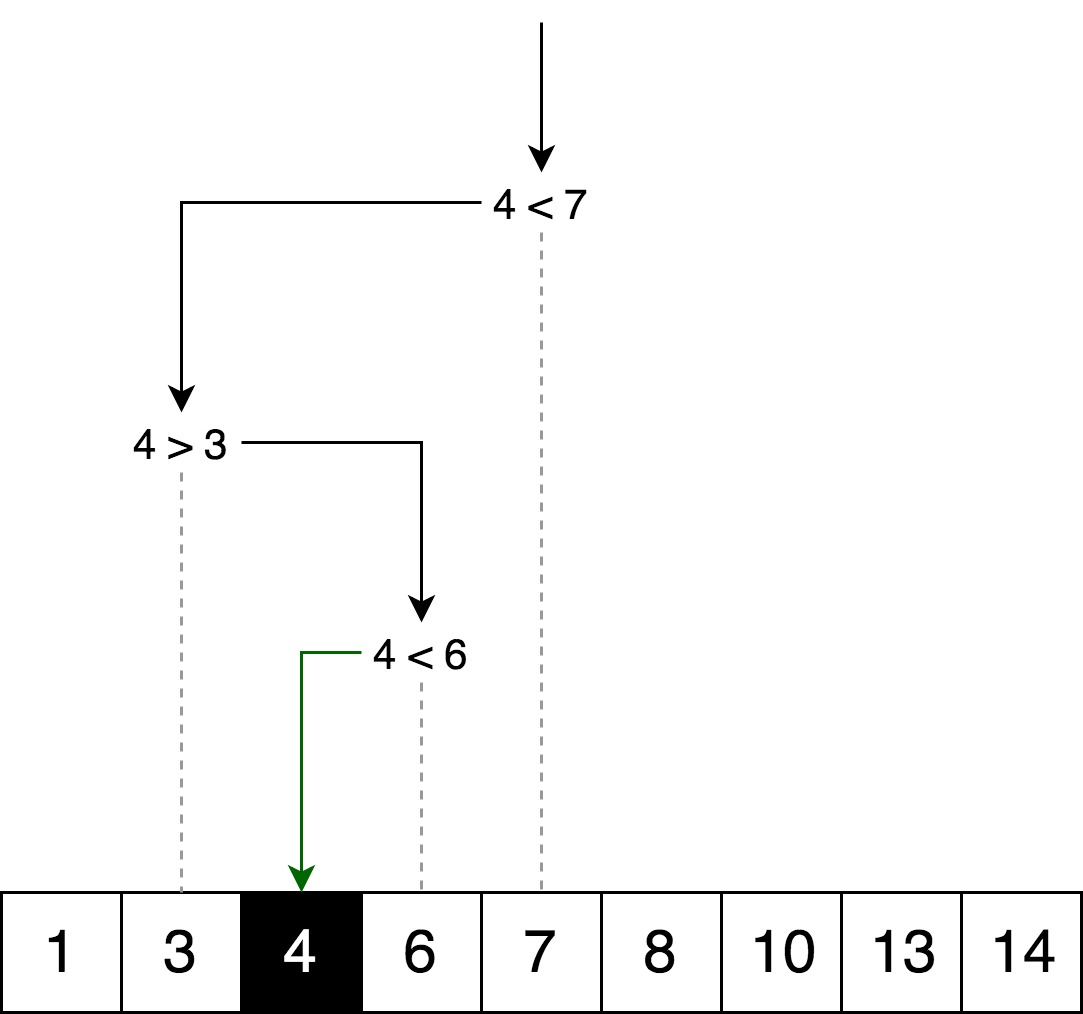
Vamos retratar a mesma lógica de pesquisa, mas na forma de uma "árvore de decisão".
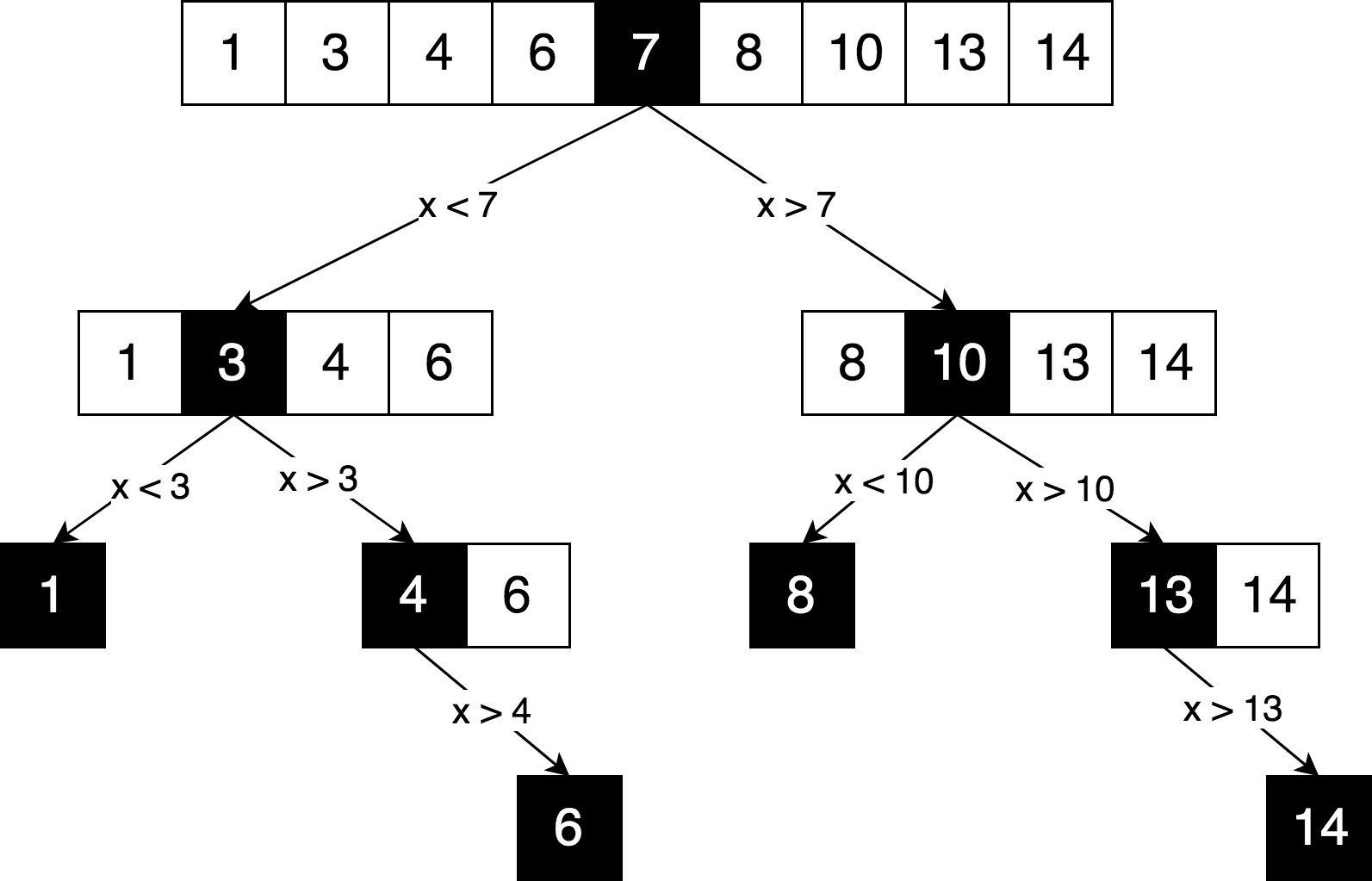
Você pode ver neste diagrama um princípio claro de "dividir e conquistar", usado para resolver esse problema. Iterativamente, dividimos nossa matriz original em sub-matrizes e tentamos encontrar o elemento que estamos procurando.
Podemos resolver esse problema usando programação dinâmica?
Não. Pelo motivo que esta tarefa
não contém subproblemas que se cruzam . Cada vez que dividimos uma matriz em partes, ambas são completamente independentes e não se sobrepõem. E de acordo com as suposições e limitações da programação dinâmica que discutimos acima, os subproblemas devem se sobrepor de alguma forma,
devem ser repetitivos .
Geralmente, sempre que uma árvore de decisão se parece exatamente com uma
árvore (e
não como um gráfico ), isso provavelmente significa que não há subproblemas sobrepostos,
Implementação de algoritmoAqui você pode encontrar o código fonte completo do algoritmo de busca binária com testes e explicações.
function binarySearch(sortedArray, seekElement) { let startIndex = 0; let endIndex = sortedArray.length - 1; while (startIndex <= endIndex) { const middleIndex = startIndex + Math.floor((endIndex - startIndex) / 2);
Exemplo de programação dinâmica: distância de edição
Geralmente, quando se trata de explicar a programação dinâmica,
a função Fibonacci é usada como exemplo. Mas, no nosso caso, vamos dar um exemplo um pouco mais complexo. Quanto mais exemplos, mais fácil é entender o conceito.
A distância de edição (ou a distância de Levenshtein) entre duas linhas é o número mínimo de operações para inserir um caractere, excluir um caractere e substituir um caractere por outro, necessário para transformar uma linha em outra.
ExemploPor exemplo, a distância de edição entre as palavras "gatinho" e "sentado" é 3, porque você precisa executar três operações de edição (duas substituições e uma inserção) para converter uma linha em outra. E é impossível encontrar uma opção de conversão mais rápida com menos operações:
- gatinho → gatinho (substituindo "k" por "s")
- sitten → sittin (substituindo "e" por "i")
- sentado → sentado (insira “g” completamente).
Aplicação de algoritmoO algoritmo possui uma ampla gama de aplicações, por exemplo, para verificação ortográfica, sistemas de correção de reconhecimento óptico, pesquisa imprecisa de cadeias, etc.
Definição matemática de um problemaMatematicamente, a distância de Levenstein entre duas linhas
a, b (com comprimentos | a | e
|b| respectivamente) é determinada pela
function lev(|a|, |b|) , em que:
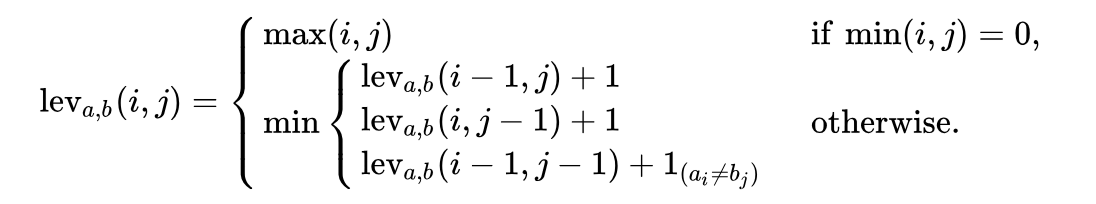
Observe que a primeira linha na função
min corresponde à operação de
exclusão , a segunda linha corresponde à operação de
inserção e a terceira linha corresponde à operação de
substituição (caso as letras não sejam iguais).
ExplicaçãoVamos tentar descobrir o que essa fórmula nos diz. Veja um exemplo simples de como encontrar a distância mínima de edição entre as linhas
ME e
MY . Intuitivamente, você já sabe que a distância mínima de edição é uma (
1 ) operação de substituição (substitua "E" por "Y"). Mas vamos formalizar nossa solução e transformá-la em uma forma algorítmica, para poder resolver versões mais complexas desse problema, como transformar a palavra
sábado em
domingo .
Para aplicar a fórmula à transformação ME → MY, primeiro devemos descobrir a distância mínima de edição entre ME → M, M → MY e M → M. Em seguida, devemos escolher o mínimo de três distâncias e adicionar uma operação (+1) da transformação E → Y.
Portanto, já podemos ver a natureza recursiva dessa solução: a distância mínima de edição ME → MY é calculada com base nas três transformações possíveis anteriores. Assim, já podemos dizer que este é um algoritmo de divisão e conquista.
Para explicar melhor o algoritmo, vamos colocar nossas duas linhas em uma matriz:
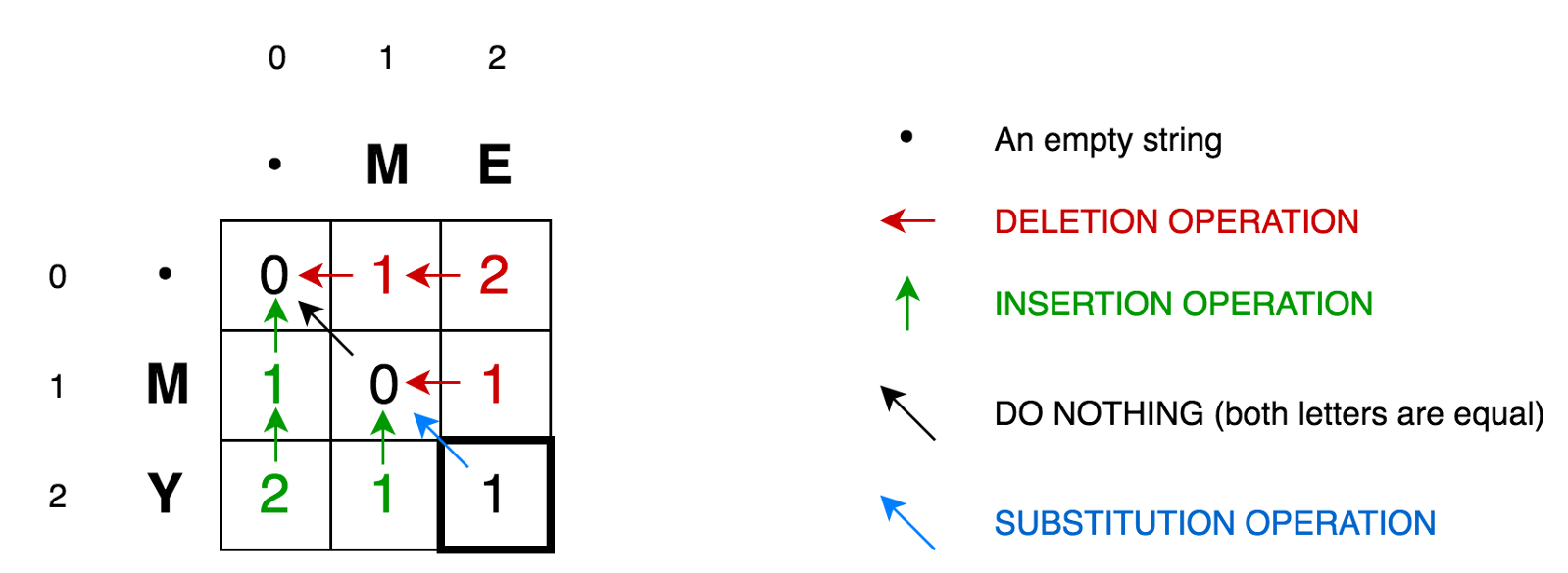A célula (0,1) contém o número vermelho 1. Isso significa que precisamos executar 1 operação para converter M em uma sequência vazia - excluir M. Portanto, marcamos esse número em vermelho.
A célula (0,2) contém um número vermelho 2. Isso significa que precisamos executar 2 operações para transformar a string ME em uma string vazia - exclua E, exclua M.
A célula (1,0) contém um número verde 1. Isso significa que precisamos de 1 operação para transformar uma string vazia em M - colar M. Marcamos a operação de inserção em verde.
A célula (2,0) contém um número verde 2. Isso significa que precisamos executar 2 operações para converter uma string vazia em uma string MY - insira Y, insira M.
A célula (1,1) contém o número 0. Isso significa que não precisamos executar nenhuma operação para converter a string M em M.
A célula (1,2) contém o número vermelho 1. Isso significa que precisamos executar 1 operação para transformar a sequência ME em M - excluir E.
E assim por diante ...
Não parece difícil para matrizes pequenas, como a nossa (apenas 3x3). Mas como podemos calcular os valores de todas as células para matrizes grandes (por exemplo, para uma matriz 9x7 na transformação sábado → domingo)?
A boa notícia é que, de acordo com a fórmula, tudo o que precisamos para calcular o valor de qualquer célula com coordenadas
(i,j) são apenas os valores de 3 células vizinhas
(i-1,j) ,
(i-1,j-1) e
(i,j-1) . Tudo o que precisamos fazer é encontrar o valor mínimo de três células vizinhas e adicionar uma (+1) a esse valor se tivermos letras diferentes na i-ésima linha e j-ésima coluna.
Então, novamente, você pode ver claramente a natureza recursiva dessa tarefa.
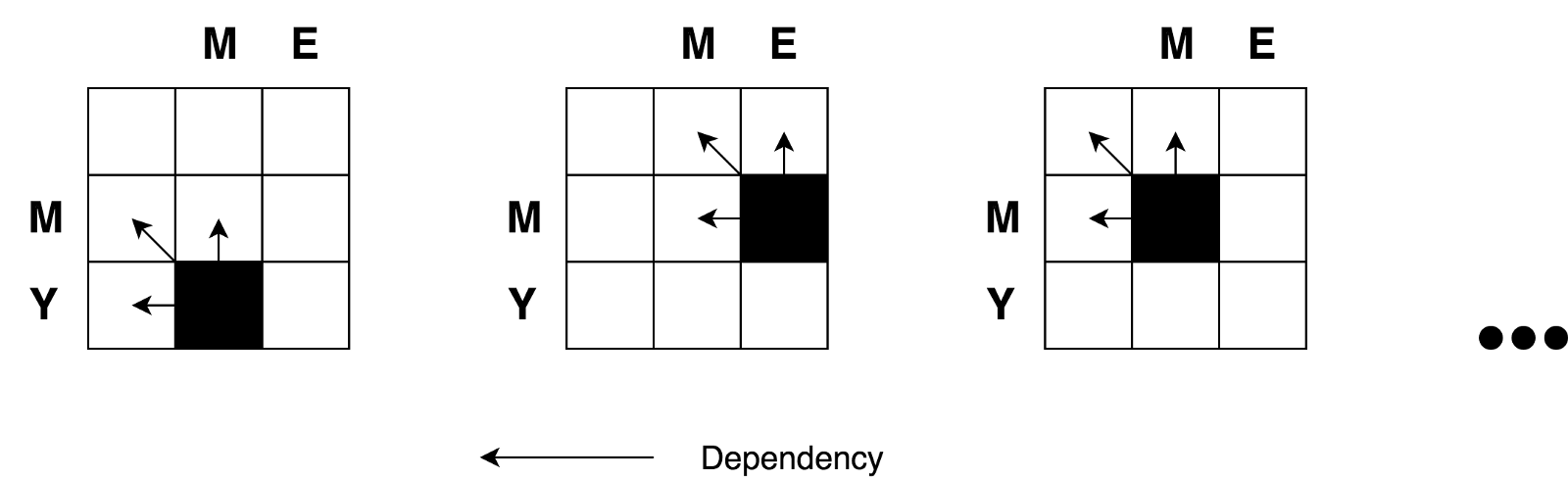
Também vimos que estávamos lidando com uma tarefa de dividir e conquistar. Mas, podemos aplicar programação dinâmica para resolver esse problema? Essa tarefa satisfaz as condições de "
problemas de interseção " e "
subestruturas ótimas " mencionadas acima?
Sim Vamos construir uma árvore de decisão.
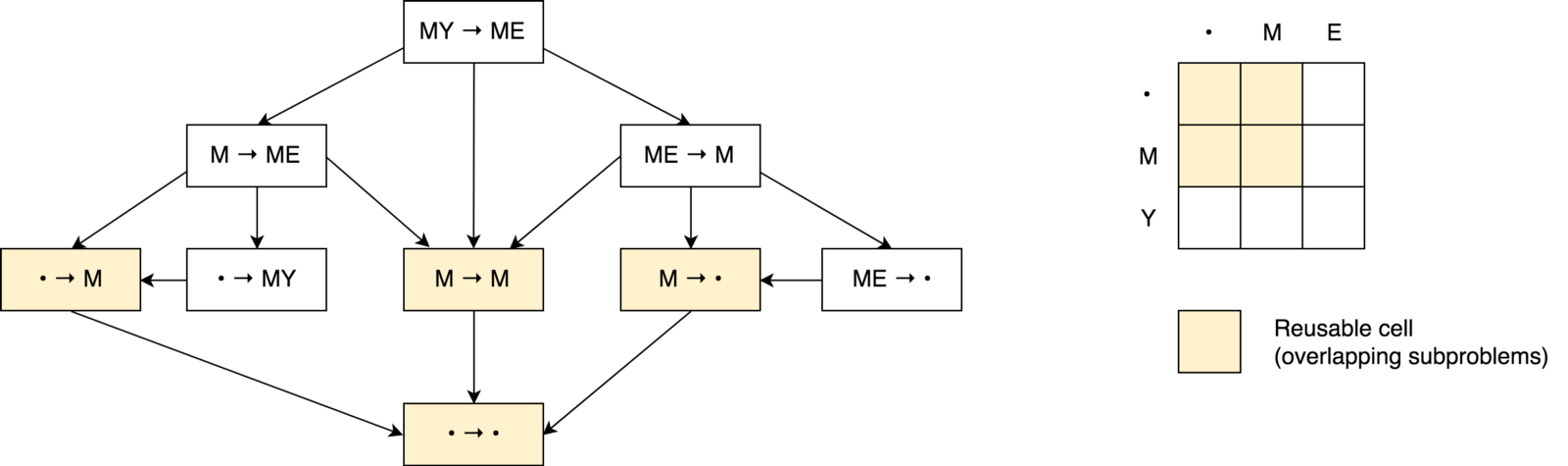
Primeiro, você pode perceber que nossa árvore de decisão se parece mais com um
gráfico de decisão do
que com uma
árvore . Você também pode observar
várias subtarefas sobrepostas . Também é visto que é impossível reduzir o número de operações e torná-lo menor que o número de operações dessas três células vizinhas (subproblemas).
Você também pode perceber que o valor em cada célula é calculado com base nos valores anteriores. Portanto, neste caso, a técnica de
tabulação é usada (preenchendo o cache na direção de baixo para cima). Você verá isso no exemplo de código abaixo.
Aplicando todos esses princípios, podemos resolver problemas mais complexos, por exemplo, a tarefa de transformação Sábado → Domingo:
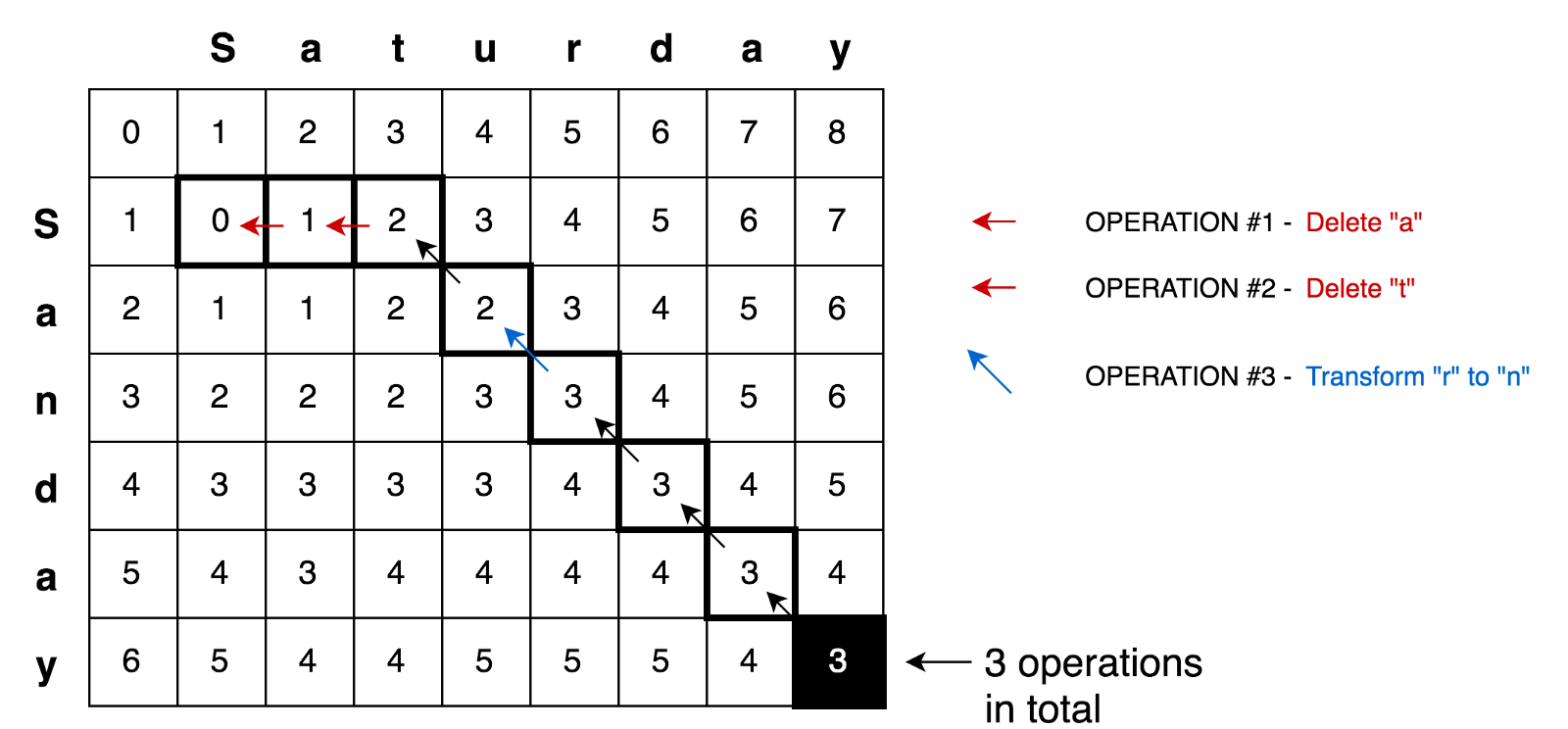Exemplo de códigoAqui você encontra uma solução completa para encontrar a distância mínima de edição com testes e explicações:
function levenshteinDistance(a, b) { const distanceMatrix = Array(b.length + 1) .fill(null) .map( () => Array(a.length + 1).fill(null) ); for (let i = 0; i <= a.length; i += 1) { distanceMatrix[0][i] = i; } for (let j = 0; j <= b.length; j += 1) { distanceMatrix[j][0] = j; } for (let j = 1; j <= b.length; j += 1) { for (let i = 1; i <= a.length; i += 1) { const indicator = a[i - 1] === b[j - 1] ? 0 : 1; distanceMatrix[j][i] = Math.min( distanceMatrix[j][i - 1] + 1,
Conclusões
Neste artigo, comparamos duas abordagens algorítmicas (“programação dinâmica” e “dividir e conquistar”) com a solução de problemas. Descobrimos que a programação dinâmica usa o princípio de "dividir e conquistar" e pode ser aplicada à solução de problemas se o problema contiver subproblemas que se cruzam e a subestrutura ideal (como é o caso da distância de Levenshtein). A programação dinâmica ainda usa técnicas de memorização e tabulação para preservar as sub-resoluções para reutilização posterior.
Espero que este artigo esclareça e não complique a situação para aqueles que tentaram lidar com conceitos importantes como programação dinâmica e "dividir e conquistar" :)
Você pode encontrar mais exemplos algorítmicos usando programação dinâmica, com testes e explicações no repositório
JavaScript Algorithms and Data Structures .
Codificação bem sucedida!