É fácil. Tomamos a métrica de Schwarzschild, procuramos os símbolos de Christoffel, calculamos sua derivada, escrevemos a equação geodésica, alteramos algumas coordenadas cartesianas (para não sofrer), obtemos uma grande ODE com várias linhas - e resolvemos. Algo assim. "



Agora está claro que os buracos negros me chuparam. Eles são infinitamente fascinantes. Na última vez, descobri como visualizar a geometria de Schwarzschild. Eu estava absorto no problema de uma representação precisa de como a curvatura de tal espaço-tempo afeta a aparência do céu (já que os fótons de fontes distantes se movem ao longo de linhas geodésicas curvadas por um buraco negro) para criar uma simulação interativa. Aqui está o resultado (funciona no navegador). O truque é maximizar o cálculo do desvio dos raios de luz. Tudo funciona mais ou menos normalmente, mas é claro que essa simulação está longe de ser ideal, porque na realidade nenhum rastreamento é feito lá (para não especialistas: restauração da localização dos raios de luz que caem na câmera no tempo).

Meu novo projeto corrige essa falha abandonando a eficiência / interatividade da maneira mais simples: este é um rastreador de roteador puro na CPU . O rastreamento é realizado com a maior precisão e o maior tempo possível. A renderização da imagem acima levou 15 a 5 minutos (obrigado, RK4) no meu laptop.

Não há melhorias em comparação com trabalhos semelhantes. Eu realmente gosto de fazer isso. Estou escrevendo este artigo para compartilhar não apenas os resultados, como a imagem acima ( principalmente porque outros se saíram melhor ), mas também o processo de criação dessas imagens , com uma discussão / explicação da física e implementação. Idealmente, isso pode inspirar ou se tornar um guia para pessoas com interesses semelhantes.

Procure renderizações novas com a tag starless no tumlr.

Um pouco de óptica pseudo-Riemann

Sombra

Se você já experimentou meu applet , está familiarizado com esta imagem:



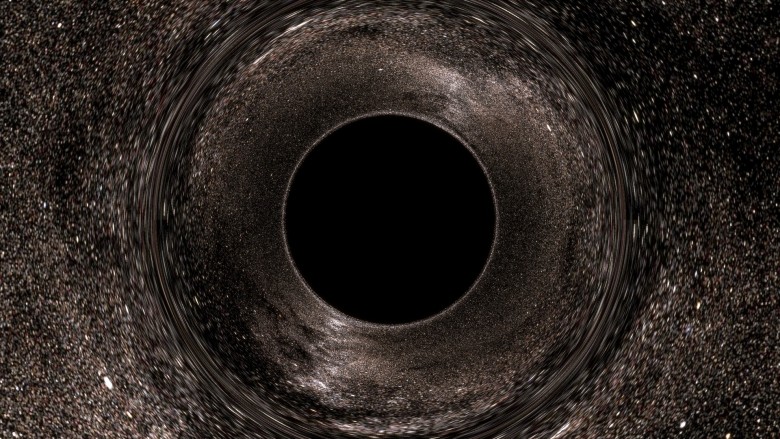
Ele destaca as principais características: um disco preto e um estranho anel de distorção.

As discussões costumam prestar atenção: é errado dizer que um disco preto é um horizonte de eventos. De fato, é errado dizer que a área da imagem é um objeto . Esta é uma imagem de um objeto. De fato, existem trajetórias que, ao rastrear do seu olho até a fonte, aparecerão no horizonte de eventos (GS). Estes são pixels pretos, já que nenhum fóton pode seguir esse caminho de um buraco negro (BH) até o olho. Portanto, esse disco preto é claramente uma imagem do horizonte de eventos , no sentido de que se você desenhar (no passado distante) algo diretamente acima do horizonte, os observadores externos poderão vê-lo diretamente nesse disco preto (na verdade, executaremos isso experimente mais tarde). Em algumas publicações, essa região negra também é chamada de “sombra” de BH.



No entanto, é interessante notar que esta também é uma imagem da esfera de fótons (PS). O gráfico gnuplot na parte superior mostra a geodésia dos fótons recebidos do infinito (olhando a BH à distância ao aplicar zoom) junto com GS (preto) e FS (verde). O raio da esfera de fótons é 1,5 vezes maior que o raio do horizonte de eventos (na geometria de Schwarzschild) e aqui as órbitas circulares dos fótons ao redor do buraco negro são permitidas (embora instáveis). No gráfico, alguns raios caem na inexistência, enquanto outros estão dispersos (e, assim, aparecem em outro ponto da esfera celeste). Pode-se observar que, para os raios absorvidos, o parâmetro de exposição é menor que ~ 2,5 raios. Esse é o raio aparente do disco preto e é muito maior que o GS e o FS.

De qualquer forma, o seguinte fato é importante:

Um incidente de raio de luz livremente na esfera de fótons também alcançará o horizonte de eventos.

Isso significa que a imagem da esfera de fótons é incluída na imagem do horizonte de eventos. Mas como o GS está claramente localizado dentro do FS, a imagem do primeiro também deve ser um subconjunto do último. Então as duas imagens devem corresponder.

Por que verificamos que o disco preto também é uma imagem do FS? Porque isso significa que a borda do disco preto é preenchida com fótons que deslizam ao longo da esfera de fótons. O pixel imediatamente fora do disco preto corresponde a um fóton, que (ao voltar para trás) cai espiralmente na esfera do fóton, cada vez mais perto de uma órbita circular instável, girando muitas vezes (quanto mais perto você olha, mais rápido ele gira) e depois aparece em espiral - já que a órbita é instável - e escapa ao infinito.

Esse comportamento causará um efeito óptico interessante semelhante à separatriz em um sistema dinâmico. Teoricamente, se o feixe for lançado exatamente ao longo da borda, ele girará para sempre em espiral, cada vez mais perto da órbita circular da esfera de fótons.

Influência na esfera celestial

Não focaremos neste tópico, porque o último applet é dedicado a ele e oferece uma idéia muito melhor de distorções no céu (incluindo a opção de grade UV para distorções mais nítidas).

Apenas algumas palavras sobre o anel de Einstein. A lente gravitacional é opticamente distinguível porque é uma imagem de um único ponto, localizado diretamente em frente ao observador. O anel é formado em um ângulo de visão quando os raios do observador são dobrados em paralelo. Os raios externos não são suficientemente curvos e permanecem divergentes; por dentro, dobram-se demais, convergem e, na realidade, podem até retroceder ou circular, como vimos.

Mas pense sobre isso: se você se aproximar o suficiente do disco preto, os raios de luz podem formar um círculo e depois paralelamente. Lá devemos ver o anel secundário de Einstein. De fato, pode haver anéis de qualquer ordem (qualquer número de enrolamentos). Também deve haver anéis "ímpares" entre eles, onde os raios de luz dobram em paralelo, mas são direcionados para o espectador. Essa série interminável de anéis existe, mas é completamente invisível em nossa imagem (de fato, na maioria dessas imagens), porque está muito perto da borda do disco.

Distorção do horizonte de eventos

Algo mudou nesta nova imagem. Antes de tudo, é feita com melhor resolução e com filtragem de fundo para torná-lo mais distinguível. Aumentei o zoom na imagem de BH (não nos aproximando, ainda estamos a uma distância de ~ 10 raios dela, apenas um zoom). Mas o mais importante, desenhei uma grade no horizonte .

O horizonte é "apenas uma esfera". Tecnicamente, não é uma esfera riemanniana padrão com uma métrica espacial. O horizonte é como a luz! Esta é uma maneira colorida de dizer que viaja na velocidade da luz. No entanto, nas coordenadas de Schwarzschild, ainda é uma superfície $$$r = 1$ e podemos usar $$$\ phi$ e $$$\ theta$ como longitude e latitude. Assim, uma grade pode ser desenhada de maneira canônica. Você a vê na imagem.

A grade permite que você veja um efeito especial que pode ser derivado se analisarmos a curva de dispersão / absorção dos fótons acima:

Toda a superfície do horizonte é visível simultaneamente a partir de qualquer ponto.

Isso é muito interessante. Quando você olha para uma esfera fixa em um espaço-tempo plano padrão, não vê mais de 50% de sua superfície a qualquer momento (se você se aproximar, é menos de 50% devido à perspectiva). Mas o horizonte é visível ao mesmo tempo que um disco preto: preste atenção, em particular, aos pólos norte e sul. No entanto, embora toda a superfície seja colocada em um disco preto, ela não a cobre inteiramente : se você ampliar a borda, verá que a imagem da GE termina no final da sombra. Você encontrará um anel localizado muito perto da borda externa, mas não até o fim. Esta imagem é um ponto oposto ao observador e define os limites dessa “primeira” imagem do HS dentro. Então, o que há entre este anel e a borda real? Ainda não gerei uma imagem ampliada, mas há outra imagem inteira do horizonte de eventos . E então mais um, e mais um, até o infinito. Existem infinitas imagens concêntricas de todo o horizonte, comprimidas na sombra. (Muito obrigado / u / xXxDeAThANgEL99xXx por apontar esse fenômeno que eu perdi) .

Adicionando um disco de acreção

O que a renderização moderna de BH fará sem um disco de acréscimo? Embora essa seja claramente uma questão discutível, o interestelar de Nolan está realmente disponível para observação, sem mencionar a precisão, mas definitivamente temos que agradecer ao sucesso de público por popularizar uma distorção específica do disco de acreção. Aqui temos um disco de acreção horizontal infinitamente fino, plano e que se estende da esfera de fótons (embora isso seja muito irrealista porque as órbitas são mais baixas $$$3r_S$ instável, como descrito abaixo) até 4 raios, pintados em uma gaiola branca e azul. Com essa cor, é óbvio que nos deparamos com outro caso, quando ao mesmo tempo 100% da superfície do objeto é visível.

Para esta imagem, movi o observador um pouco mais alto para olhar o disco um pouco de cima. Você vê imagens de duas faces do disco : superior e inferior. A imagem é dobrada por um arco sobre a sombra do buraco negro, porque o feixe direcionado diretamente acima do buraco negro se curva para encontrar a superfície superior do disco atrás do buraco, em frente ao observador.

Isso também explica a própria existência da imagem inferior: os raios que passam sob a BH são curvados para a superfície inferior do disco, que fica atrás da BH. Se você olhar com atenção, a imagem se espalha pela sombra, mas na parte superior é muito mais fina. Isso corresponde aos raios de luz que vão acima da BH, fazem um círculo quase completo ao redor do buraco e atingem a superfície inferior na frente do disco.

Obviamente, é fácil concluir que existe um número infinito de imagens de discos de acúmulo que diminuem muito rapidamente à medida que se aproximam da borda. A próxima imagem já é muito fina, quase invisível na parte inferior da borda.

GIFs ainda são relevantes

Nesta animação convulsiva, ligo / desligo a deflexão da luz (formalmente Schwarzschild / Minkowski) para esclarecer alguns dos pontos de que falamos.





Esses dois gifs estranhos são criados a pedido dos leitores. No primeiro, o observador circula em torno de um buraco negro a uma distância de 10 raios. Isso não deve ser entendido como uma órbita real, uma vez que, na realidade, não há aberrações ao se mover em órbita. Aqui está uma série de imagens estacionárias de BH de vários pontos em que o observador se move de um lugar para outro entre os quadros; é uma órbita "adiabática", se quiser.

E estéreo ainda é relevante

Curiosamente, a sombra parece bastante plana.

Ciência suficiente

Temos fotos informativas suficientes no estilo dos anos 90 em baixa resolução e com cores venenosas. Aqui estão algumas representações “pop” (clique para ver em tamanho real).


Esta imagem foi gerada pelo usuário / n / dfzxh com super amostragem quatro vezes maior


Plano maior


Imagem ampliada do anel


O efeito cult do "anel de luz" quando visto do plano equatorial


Se você baixar o programa, esta é a cena atual por padrão


Uma unidade muito mais ampla

Bem, sim, nada de especial. Não há obras de arte, apenas renderizações do programa. Voltemos temporariamente à ciência: a terceira imagem , que parece não ter significado, é realmente muito valiosa. Essa é a área ampliada entre a borda superior do disco preto e a imagem principal do disco de acúmulo. O observador está na borda externa do disco de acréscimo e aproxima a imagem. O objetivo era representar o maior número possível de anéis de ordens diferentes. Três ordens são visíveis: a zona mais clara na parte superior é apenas a borda inferior da primeira imagem da superfície mais distante do disco. A barra abaixo, sob o mar calmo de estrelas esticadas, é a parte superior da imagem da frente inferior do disco. No fundo - uma fina linha de luz com largura não superior a um pixel, colada no disco preto da esfera de fótons. Esta é basicamente a terceira imagem: novamente, a superfície superior distante, mas depois que a luz completa uma revolução adicional ao redor do buraco negro. Mescladas com ela, mas imagens cada vez mais finas são anéis de ordem superior. Bem, isso também é digno da tag <blockquote>:

Existem infinitas imagens das superfícies superior e inferior do disco de acréscimo e todas mostram a superfície inteira do disco ao mesmo tempo. Além disso, exceto pela primeira, essas imagens não passam nem na frente do disco preto nem na frente uma da outra e, portanto, são "concêntricas".

Maravilhoso.

Aceito pedidos de renderização
Interessado em uma visualização específica, mas não está pronto para enfrentar as dificuldades de instalar o programa e se renderizar? Apenas envie- me um reddit ou envie- me um e-mail. A renderização em 1080p no meu laptop não leva mais que 10 a 20 minutos.

Disco de acréscimo realista

O disco de acreção nas renderizações é bem caricatural. É apenas um disco estúpido de textura. O que acontece quando a física real é incluída na aparência visual de um disco? O que acontece quando você considera o desvio para o vermelho do movimento orbital, por exemplo?

Um modelo popular de um disco de acreção é um disco infinitamente fino de matéria em uma órbita quase circular. Começa com o ISCO (a órbita circular estável mais interna, $$$3r_s$ ) com um perfil de temperatura de acordo com uma lei de energia $$$(T \ sim r ^ {- a}$ . Vou usar uma opção muito simples:

$$

$$T \ sim r ^ {- 3/4}$$

o que é definitivamente anormal na teoria geral da relatividade para fluidos realistas, mas aqui está (em qualquer caso, você não notará a diferença).

Agora, um parâmetro livre é uma escala comum para temperaturas, por exemplo, a temperatura no ISCO. Essa temperatura é enorme para a maioria dos buracos negros. Estamos falando de centenas de milhões de Kelvin; é difícil imaginar qualquer artefato humano que possa existir sob a influência da radiação do disco (pico da radiação de raios-x) nessas temperaturas, sem mencionar a fotografia. Então, claramente precisamos diminuir a temperatura. Obviamente, buracos negros supermassivos são mais frios, mas não o suficiente. Precisamos cair para 10.000 K no ISCO para que possamos pelo menos ver alguma coisa. Isso é muito impreciso, mas é tudo o que posso fazer.

Duas perguntas devem ser feitas. Primeiro: qual a cor do corpo preto nessa temperatura? Segundo: quão brilhante é ? Formalmente, a resposta para essas duas perguntas está no produto escalar de funções que descrevem os canais R, G, B com o espectro do corpo negro. Na prática, algumas aproximações são usadas.

Para a fórmula de Tanner Helland , é precisa e eficaz para cores, mas inclui inúmeras condições que não são viáveis ​​com o meu traçado de raios (veja abaixo para mais detalhes). A maneira mais rápida é usar uma textura simples:



Essa textura é uma das muitas coisas úteis na seleção de Mitchell Charity de “De que cor é o corpo preto?” . Para referência, corresponde ao ponto branco E (ponto branco E).

A escala mostra a cor de um corpo preto a temperaturas de 1000 K a 30 000 K, com temperaturas mais altas correspondendo ao mesmo tom de azul. Como existe uma enorme diferença de brilho entre as temperaturas, essa textura não pode e não transmite brilho; ao contrário, normaliza as cores. Nossa tarefa é calcular o brilho relativo e aplicá-lo. Uma fórmula analítica é adequada para isso. Se assumirmos que o espectro visível é muito estreito, a intensidade visível total é proporcional ao espectro do próprio corpo negro:

$$

$$\ frac {1} {\ lambda ^ 5} \ frac {1} {\ exp (\ frac {hc} {\ lambda k_B T}) - 1}$$

onde me livrei de constantes comuns estúpidas (ainda vamos escalar o brilho para ver alguma coisa). Você pode simplesmente inserir $$$\ lambda$ aproximadamente para a faixa visível do espectro, e obtemos que o brilho é proporcional à temperatura de acordo com esta fórmula:

$$

$$(e ^ {\ frac {29622,4 \ text {K}} {T}} - 1) ^ {- 1}$$

É bem simples Como verificação, observamos que a intensidade relativa cai rapidamente para zero quando T se aproxima de zero e praticamente não muda quando T chega ao infinito.

Redshift

Discutimos velocidades orbitais na geometria de Schwarzschild na descrição do applet. Para calcular o desvio para o vermelho, é usada a fórmula de desvio para o vermelho do SRT:

$$

$$(1 + z) _ \ text {Doppler} = \ frac {1 - \ beta \ cos (\ theta)} {\ sqrt {1- \ beta ^ 2}}$$

Onde como $$$\ cos (\ theta)$ - o cosseno do ângulo entre a direção do feixe emitido pelo disco e a velocidade local do disco, calculado no sistema de coordenadas inerciais locais de Schwarzschild. A fórmula é verdadeira neste contexto devido ao princípio da equivalência.

Deve ser multiplicado pelo coeficiente de desvio para o vermelho gravitacional:

$$

$$(1 + z) _ \ text {Gravitacional} = (1 - r ^ {- 1}) ^ {- 1/2}$$

esse coeficiente não depende da trajetória do feixe de luz, mas apenas do raio de radiação, uma vez que a geometria de Schwarzschild é estacionária.

Isso também significa que a contribuição da posição do observador para o desvio para o vermelho gravitacional é constante em todo o campo de visão. Toda a nossa imagem tem uma constante mudança geral de azul, porque estamos no fundo de BH. Portanto, esse efeito fornece apenas uma tonalidade fraca que pode ser ignorada.

Também negligenciamos o desvio para o vermelho do movimento do observador, porque nosso observador é estacionário na geometria de Schwarzschild. Aqui está o resultado final:



Como você pode ver, a maior parte do disco é completamente branca devido ao brilho máximo nos canais de cores. Se você abaixar esses canais no intervalo de 0,0 a 1,0, as partes externas do disco ficarão pálidas ou pretas.O aumento do brilho é muito grande para ser visto e apreciado. Tentei mostrar o efeito usando o pós-processamento para que as partes mais brilhantes mostrassem uma transição de cores, mas isso não é suficiente.

Imagem bastante confusa. Aqui está uma imagem sem levar em conta o brilho, onde você pode avaliar as cores:



Essas fotos têm uma resolução mais baixa, porque levam muito tempo para serem renderizadas no meu laptop (raízes quadradas são ruins, crianças).

De qualquer forma, essa renderização é mil vezes menos espetacular do que as outras (principalmente porque a borda interna do disco já está suficientemente distante do GS, portanto as lentes são muito grandes), mas a renderização é pelo menos precisa . Se você encontrar um buraco negro com uma temperatura de 10.000 K e bons óculos de sol, verá exatamente isso.

Outra foto em close. Aumentei artificialmente a saturação da beleza:

Escrevendo um traçador de raios do buraco negro

Fonte do Github

Há uma diferença muito grande e óbvia entre a ótica dos buracos negros e o integrador numérico, que produz belos papéis de parede com uma resolução de 1080p. Na última vez, não publiquei meu raciocínio, mas simplesmente criei um repositório git grande e sujo. Agora, quero explicar um pouco mais detalhadamente e também tentar manter o código de forma mais precisa e com comentários.

Meu marcador não foi criado bom, poderoso, rápido. Antes de tudo, eu queria que fosse fácil de configurar, simplificá-lo, para que as pessoas pudessem se inspirar e ver o potencial de melhoria: até sua imperfeição pode incentivar alguém a decidir escrever sua própria versão. Aqui está uma breve visão geral dos algoritmos e sua implementação.

Potencial "mágico"

Então, a teoria geral da relatividade, tudo está claro. É fácil Tomamos a métrica de Schwarzschild, procuramos os símbolos de Christoffel, calculamos sua derivada, anotamos a equação geodésica, alteramos algumas coordenadas cartesianas para evitar sofrimento sem fim, obtemos uma enorme ODE de várias linhas, resolvemos. Algo assim.

Brincadeira. Claro, há um truque.

Se você se lembra, da última vez que deduzi a seguinte equação para a órbita de uma partícula sem massa em seu plano orbital na geometria de Schwarzschild ($$$u=1/r$ ):

$$

$$u''(\phi) + u = \frac{3}{2} u^3$$

O truque é ver a fórmula Binet aqui . Para uma massa de uma partícula newtoniana no potencial newtoniano do campo de forças centrais:

$$

$$\frac{d^2}{dt^2} \vec x = \frac{1}{m} F(r)$$

então a partícula obviamente se moverá em seu plano orbital e corresponde à fórmula de Binet para $$$u(\phi)$ :

$$

$$u'' + u = - \frac{1}{m h^2 u^2} F(u)$$

Onde $$$\frac{d}{d\phi}$ É um número primo $$$m$ - massa e $$$h$- momento angular por unidade de massa. Esta é uma equação para órbita, não uma equação de movimento. Não diz nada sobre$$$u(t)$ ou $$$phi(t)$ mostra apenas a relação entre $$$u$ e $$$\phi$ .

Vamos parar por um momento para refletir sobre o que realmente conseguimos. A equação diz que, se você imaginar um sistema mecânico hipotético de uma partícula sob a ação de uma certa força central, sua trajetória será uma solução para a fórmula de Binet. Então o sistema mecânico se torna uma calculadora de fórmula.

É isso que estou oferecendo aqui. Nós indicamos$$$m=1$ e eles pegaram (não-físico, qualquer que seja) um sistema simples de uma partícula pontual nesse campo de força específico:

$$

$$\vec F(r) = - \frac{3}{2} h^2 \frac{\hat r}{r^5}$$

onde $$$h$É uma constante constante, e resolver a equação numericamente é muito simples. Então a solução$$$\vec x (T)$ onde $$$T$ - a coordenada de tempo abstrata para este sistema é, de fato, a parametrização da única solução para a equação de Binet correspondente, que é exatamente a equação geodésica .

Portanto, resolvemos a equação newtoniana em coordenadas cartesianas, que geralmente é a mais simples (decidi usar o método Runge-Kutta para tornar possível aumentar o tamanho da etapa e reduzir o tempo de renderização, mas no futuro o usuário poderá escolher um método de solução diferente). Então temos apenas a geodésia semelhante à luz, onde $$$T$ O parâmetro está indo em frente (em contraste com o Schwarzschild $$$t$ e a partir do horário normal, que não existe).

Isso é muito melhor que o método anterior, que trabalhou com coordenadas polares no plano de órbita. Aqui os cálculos são muito eficientes.

Traçado de raios numpy

Se você olhar a fonte, verá um script Python. Horror! Por que escrever ray tracing em Python? Todo mundo sabe como os loops são executados lentamente no Python, o que sempre (quase) põe fim ao trabalho. O fato é que realizamos cálculos em numpy - e em paralelo. É por isso que este programa não poderá exibir gradualmente as partes já desenhadas na tela: renderiza tudo ao mesmo tempo.

Primeiro de tudo, criamos uma matriz de condições iniciais. Por exemplo, uma matriz (numPixel, 3) com vetores para todos os pixels da imagem (numPixel - largura da imagem × altura da imagem). Em seguida, o cálculo de cada raio é reduzido a matrizes do tipo (numPixel, ...) . Como as operações com matrizes numpy são muito rápidas e tudo é estaticamente digitado aqui (espero não estar dizendo nada estúpido agora), deve ser calculado com bastante rapidez. Talvez não seja C, mas ainda assim rápido. Ao mesmo tempo, temos a flexibilidade e a clareza do Python.

Esse método é péssimo para o traçado de raios padrão, onde os objetos têm partes difusas, refletidas e refratadas, e é importante considerar as condições de iluminação. Por exemplo, a reflexão seletiva de partes de uma série de raios é um verdadeiro pesadelo; o rastreamento de valores booleanos ou índices de loop requer várias máscaras e os loops não podem ser interrompidos. Mas aqui está outro caso: todos os objetos em nossa cena apenas emitem luz: o céu, um disco de acréscimo quente, um horizonte de eventos totalmente preto e poeira brilhante. Eles não são afetados pela luz incidente, e a própria luz também passa calmamente através deles, exceto para reduzir a intensidade. Isso nos leva a um algoritmo para determinar a cor:

Mistura de cores

Isso é fácil: você só precisa misturar todos os objetos entre nós e a fonte do raio com seus valores alfa correspondentes e colocá-los um sobre o outro, onde o mais distante estará na parte inferior. Inicializamos o buffer de cores com preto alfa-transparente e, quando nos cruzamos com o objeto, atualizamos o buffer misturando a cor do objeto em nosso buffer de cores. Realizamos as mesmas etapas para poeira (use o perfil de densidade $$$r ^ {- 2}$ ) e continue a iterar até o final. Observe que o canal alfa também funciona como um buffer Z, pois o objeto deixa de contribuir depois que o raio cruza o objeto opaco (que define o valor alfa do buffer em 1.0).

A desvantagem óbvia desse método é que você não pode interromper o traçado de raios depois de calculá-lo, porque faz parte da matriz em que o rastreamento de outros raios continua. Por exemplo, após uma colisão com o horizonte, os raios continuam vagando aleatoriamente depois que caem em uma singularidade - você pode ver o que acontece se desligar explicitamente o objeto do horizonte. O algoritmo de mistura alfa garante que eles não afetem a imagem final, mas esses raios ainda carregam a CPU.