Distribuir uniformemente pontos pela esfera em pytorch e tensorflow

Este texto foi escrito para aqueles que estão interessados ​​em aprendizado profundo, que desejam usar métodos diferentes das bibliotecas pytorch e tensorflow para minimizar a função de muitas variáveis, que estão interessados ​​em aprender como transformar um programa executado sequencialmente em cálculos de matriz vetorizada executados usando numpy. Você também pode aprender como criar um desenho animado a partir de dados visualizados usando o PovRay e o vapory.

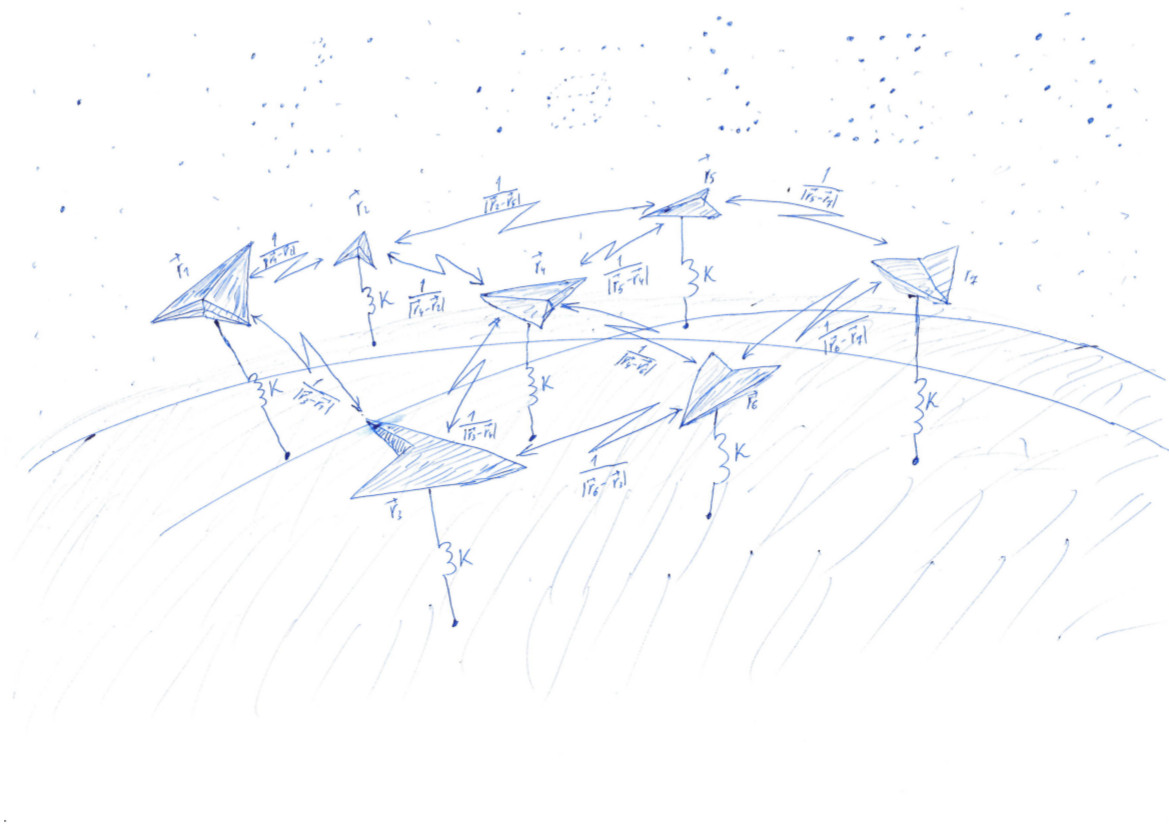
De onde vem a tarefa

Cada um minimiza sua funcionalidade (c) Anonymous Data Scientist

Em uma das publicações anteriores do nosso blog , especificamente no parágrafo "Rake No. 6", falamos sobre a tecnologia DSSM, que permite converter texto em vetores. Para encontrar esse mapeamento, é necessário encontrar os coeficientes de transformações lineares que minimizem a função de perda bastante complexa. Compreender o que acontece quando se aprende esse modelo é difícil devido à grande dimensionalidade dos vetores. Para desenvolver uma intuição que permita escolher o método de otimização e definir os parâmetros desse método, considere uma versão simplificada desta tarefa. Agora deixe que os vetores estejam em nosso espaço tridimensional habitual, para que sejam fáceis de desenhar. E a função de perda será o potencial de separar os pontos e atrair a esfera unitária. Nesse caso, a solução para o problema será uma distribuição uniforme de pontos na esfera. A qualidade da solução atual é fácil de avaliar a olho nu.

Então, procuraremos uma distribuição uniforme na esfera de uma dada quantidade $$$n$pontos. Essa distribuição às vezes é necessária para a acústica, a fim de entender em qual direção lançar uma onda em um cristal. Signalman - para descobrir como colocar satélites em órbita para obter comunicações da melhor qualidade. Meteorologista - para a colocação de estações de monitoramento meteorológico.

Para alguns $$$n$a tarefa é resolvida facilmente . Por exemplo, se $$$n = 8$, podemos pegar o cubo e seus vértices serão a resposta para o problema. Nós também temos sorte se $$$n$será igual ao número de vértices do icosaedro, dodecaedro ou outro sólido platônico. Caso contrário, a tarefa não é tão simples.

Para um número suficientemente grande de pontos, existe uma fórmula com coeficientes empiricamente selecionados ; várias outras opções estão aqui , aqui , aqui e aqui . Mas há uma solução mais universal, embora mais complexa, à qual este artigo é dedicado.

Resolvemos um problema muito semelhante ao problema de Thomson ( wiki ). Dispersão $$$n$pontos aleatoriamente e depois os atraem para uma superfície, como uma esfera, e se afastam um do outro. Atração e repulsa são determinadas pela função - potencial. No valor mínimo da função potencial, os pontos estarão na esfera mais uniformemente.

Essa tarefa é muito semelhante ao processo de aprendizado dos modelos de aprendizado de máquina (ML), durante o qual a função de perda é minimizada. Mas um cientista de dados geralmente observa como um único número diminui e podemos observar a mudança da imagem. Se conseguirmos, veremos como os pontos colocados aleatoriamente dentro do cubo com o lado 1 divergem ao longo da superfície da esfera:

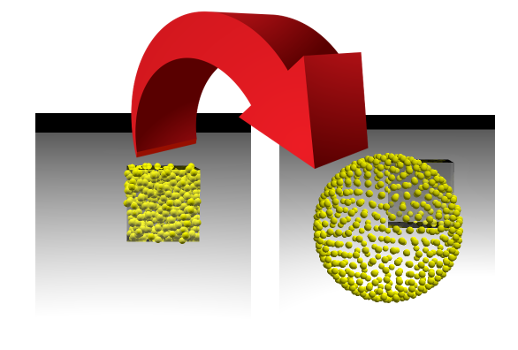
Esquematicamente, o algoritmo para resolver o problema pode ser representado da seguinte maneira. Cada ponto localizado no espaço tridimensional corresponde a uma linha da matriz $$$X$. A função de perda é calculada a partir desta matriz. $$$L$, cujo valor mínimo corresponde a uma distribuição uniforme de pontos na esfera. O valor mínimo é encontrado usando as tensorflow e tensorflow , que permitem calcular o gradiente da função de perda pela matriz $$$X$e reduza ao mínimo usando um dos métodos implementados na biblioteca: SGD, ADAM, ADAGRAD, etc.

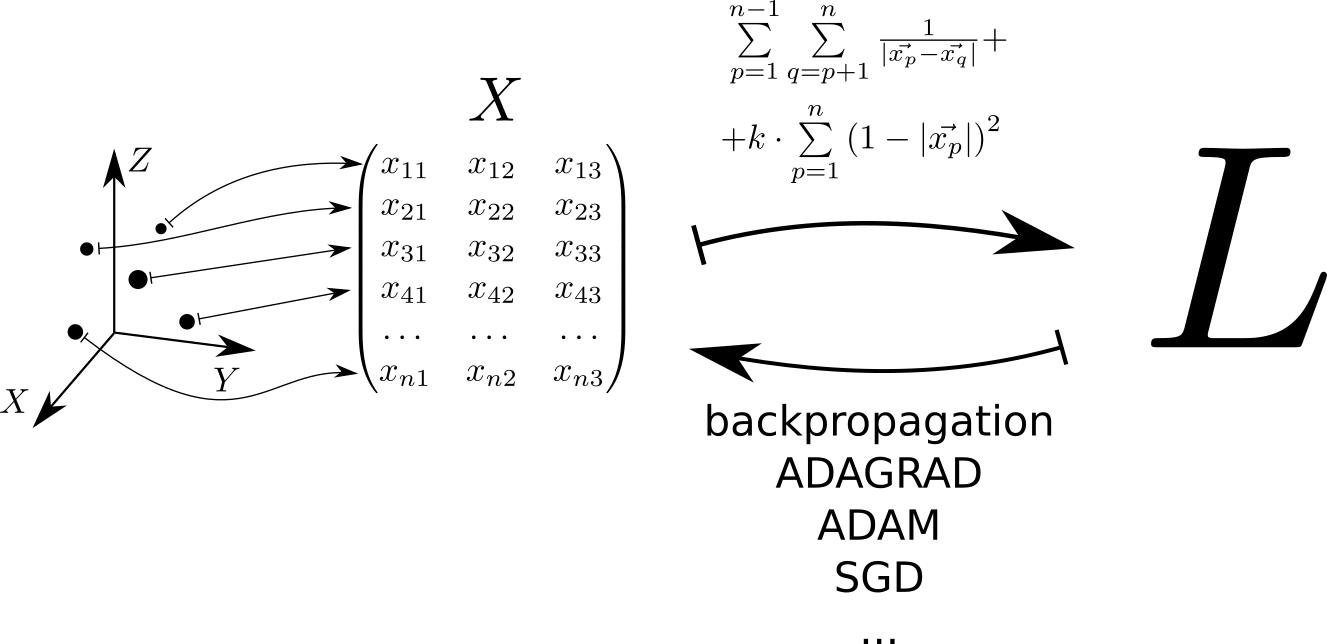
Consideramos o potencial

Devido à sua simplicidade, expressividade e capacidade de servir como uma interface para bibliotecas escritas em outros idiomas, o Python é amplamente usado para resolver problemas de aprendizado de máquina. Portanto, os exemplos de código neste artigo são escritos em Python. Para cálculos matriciais rápidos, usaremos a biblioteca numpy. Para minimizar a função de muitas variáveis ​​- pytorch e tensorflow.

Nós dispersamos aleatoriamente pontos no cubo com o lado 1. Vamos ter 500 pontos, e a interação elástica é 1000 vezes mais significativa que a eletrostática:

 import numpy as np n = 500 k = 1000 X = np.random.rand(n, 3) 

Este código gerou uma matriz $$$X$o tamanho $$ preenchido com números aleatórios de 0 a 1:

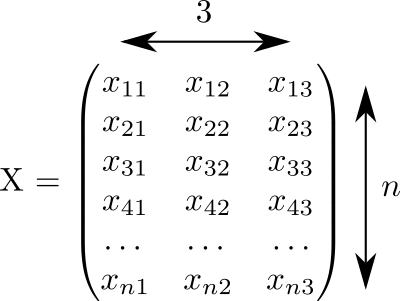
Assumimos que cada linha desta matriz corresponde a um ponto. E em três colunas as coordenadas são registradas $$$x, y, z$todos os nossos pontos.

O potencial de interação elástica de um ponto com a superfície de uma esfera unitária $$$u_1 = k \ cdot (1 - r) ^ 2/2$. Potencial de interação eletrostática de pontos $$$p$e $$$q$- $$$u_2 = 1 / | r_p - r_q |$. O potencial total consiste na interação eletrostática de todos os pares de pontos e na interação elástica de cada ponto com a superfície da esfera:

$$

$$U (x_1, ..., x_n) = \ soma \ limites _ {p = 1} ^ {n - 1} \ soma \ limites _ {q = p + 1} ^ {n} \ frac 1 {\ left | \ vec {x_p} - \ vec {x_q} \ right | } + k \ cdot \ sum \ limits _ {p = 1} ^ n \ left (1 - | \ vec {x_p} | \ right) ^ 2 \ rightarrow \ min$$

Em princípio, o valor potencial pode ser calculado usando esta fórmula:

 L_for = 0 L_for_inv = 0 L_for_sq = 0 for p in range(n): p_distance = 0 for i in range(3): p_distance += x[p, i]**2 p_distance = math.sqrt(p_distance) L_for_sq += k * (1 - p_distance)**2 #     ,     for q in range(p + 1, n): if q != p: pq_distance = 0 for i in range(3): pq_distance += (x[p, i] - x[q, i]) ** 2 pq_distance = math.sqrt(pq_distance) L_for_inv += 1 / pq_distance #      L_for = (L_for_inv + L_for_sq) / n print('loss =', L_for) 

Mas há um pequeno problema. Para um patético 2000 pontos, este programa será executado por 2 segundos. Será muito mais rápido se calcularmos esse valor usando cálculos de matriz vetorizada. A aceleração é alcançada através da implementação de operações de matriz usando as linguagens “rápidas” fortran e C, e através do uso de operações de processador vetorizadas que permitem executar uma ação em uma grande quantidade de dados de entrada em um ciclo de clock.

Vamos olhar para a matriz $$$S = X \ cdot X ^ T$. Possui muitas propriedades interessantes e é frequentemente encontrada em cálculos relacionados à teoria dos classificadores lineares no ML. Então, se assumirmos que na linha da matriz $$$X$com índices $$$p$e $$$q$vetores espaciais tridimensionais são escritos $$$\ vec {r _ p}, \ vec {r_q}$então a matriz $$$S$consistirá em produtos escalares desses vetores. Tais vetores $$$n$peças, então a dimensão da matriz $$$S$é igual a $$$n \ vezes n$.

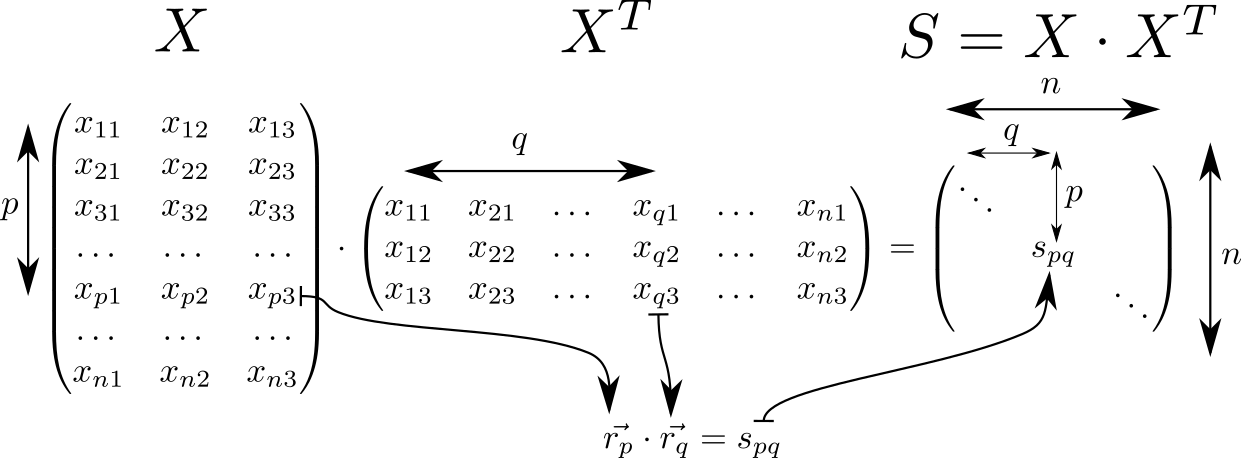
Na diagonal da matriz $$$S$quadrados de comprimentos de vetores $$$\ vec {r_p}: s_ {p}} = r_p ^ 2$ . Sabendo disso, vamos considerar todo o potencial da interação. Começamos calculando duas matrizes auxiliares. Em uma matriz diagonal $$$S$será repetido em linhas, em outro - em colunas.

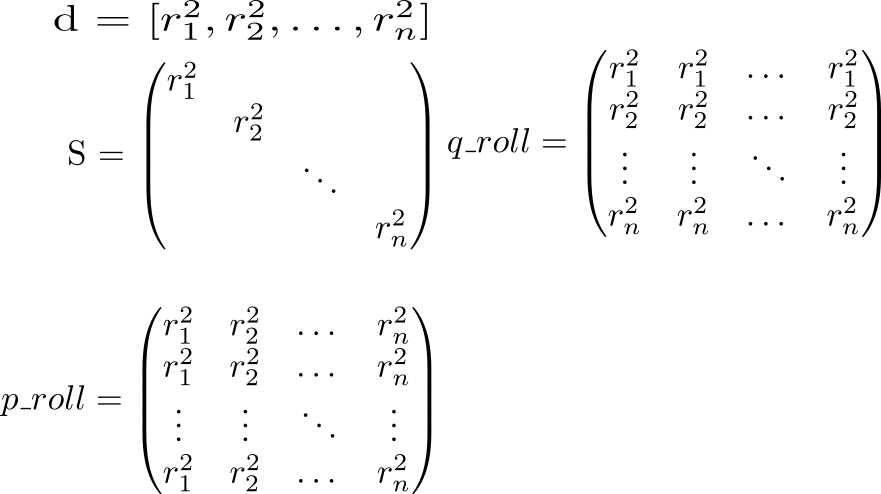
Agora, vejamos o valor da expressão p_roll + q_roll - 2 * S

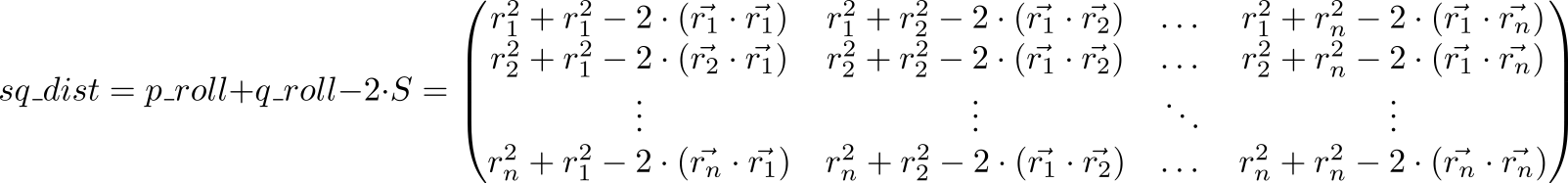
Item indexado $$$(p, q)$matriz sq_dist é igual $$$r_p ^ 2 + r_q ^ 2 - 2 \ cdot (\ vec {r_p}, \ vec {r_q}) = (\ vec {r_p} - \ vec {r_q}) ^ 2$. Ou seja, temos uma matriz de quadrados de distâncias entre pontos.

Repulsão eletrostática em uma esfera

dist = np.sqrt(sq_dist) - matriz de distâncias entre pontos. Precisamos calcular o potencial, levando em conta a repulsa de pontos entre si e a atração pela esfera. Coloque as unidades na diagonal e substitua cada elemento pelo inverso (não pense que invertemos a matriz!): rec_dist_one = 1 / (dist + np.eye(n)) . O resultado é uma matriz na diagonal da qual existem unidades, outros elementos são os potenciais da interação eletrostática entre os pontos.

Agora adicionamos o potencial quadrático de atração à superfície da esfera unitária. A distância da superfície da esfera $$$(1 - r)$. Esquadre e multiplique por $$$k$, que define a relação entre o papel da repulsão eletrostática de partículas e a atração de uma esfera. Total k = 1000 , todas as all_interactions = rec_dist_one - torch.eye(n) + (d.sqrt() - torch.ones(n))**2 . A função de perda esperada, que minimizaremos: t = all_interactions.sum()

Um programa que calcula o potencial usando a biblioteca numpy:

 S = X.dot(XT) #    pp_sq_dist = np.diag(S) #  p_roll = pp_sq_dist.reshape(1, -1).repeat(n, axis=0) #     q_roll = pp_sq_dist.reshape(-1, 1).repeat(n, axis=1) #     pq_sq_dist = p_roll + q_roll - 2 * S #      pq_dist = np.sqrt(pq_sq_dist) #    pp_dist = np.sqrt(pp_sq_dist) #      surface_dist_sq = (pp_dist - np.ones(n)) ** 2 #       rec_pq_dist = 1 / (pq_dist + np.eye(n)) - np.eye(n) #      L_np_rec = rec_pq_dist.sum() / 2 #     L_np_surf = k * surface_dist_sq.sum() #       L_np = (L_np_rec + L_np_surf) / n #   ,     print('loss =', L_np) 

Aqui as coisas estão um pouco melhores - 200 ms em 2000 pontos.

Usamos pytorch:

 import torch pt_x = torch.from_numpy(X) # pt_x -   tensor   pytorch pt_S = pt_x.mm(pt_x.transpose(0, 1)) # mm - matrix multiplication pt_pp_sq_dist = pt_S.diag() pt_p_roll = pt_pp_sq_dist.repeat(n, 1) pt_q_roll = pt_pp_sq_dist.reshape(-1, 1).repeat(1, n) pt_pq_sq_dist = pt_p_roll + pt_q_roll - 2 * pt_S pt_pq_dist = pt_pq_sq_dist.sqrt() pt_pp_dist = pt_pp_sq_dist.sqrt() pt_surface_dist_sq = (pt_pp_dist - torch.ones(n, dtype=torch.float64)) ** 2 pt_rec_pq_dist = 1/ (pt_pq_dist + torch.eye(n, dtype=torch.float64)) - torch.eye(n, dtype=torch.float64) L_pt = (pt_rec_pq_dist.sum() / 2 + k * pt_surface_dist_sq.sum()) / n print('loss =', float(L_pt)) 

E finalmente tensorflow:

 import tensorflow as tf tf_x = tf.placeholder(name='x', dtype=tf.float64) tf_S = tf.matmul(tf_x, tf.transpose(tf_x)) tf_pp_sq_dist = tf.diag_part(tf_S) tf_p_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (1, -1)), (n, 1)) tf_q_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (-1, 1)), (1, n)) tf_pq_sq_dist = tf_p_roll + tf_q_roll - 2 * tf_S tf_pq_dist = tf.sqrt(tf_pq_sq_dist) tf_pp_dist = tf.sqrt(tf_pp_sq_dist) tf_surface_dist_sq = (tf_pp_dist - tf.ones(n, dtype=tf.float64)) ** 2 tf_rec_pq_dist = 1 / (tf_pq_dist + tf.eye(n, dtype=tf.float64)) - tf.eye(n, dtype=tf.float64) L_tf = (tf.reduce_sum(tf_rec_pq_dist) / 2 + k * tf.reduce_sum(tf_surface_dist_sq)) / n glob_init = tf.local_variables_initializer() #     with tf.Session() as tf_s: #     glob_init.run() #   res, = tf_s.run([L_tf], feed_dict={tf_x: x}) #   print(res) 

Compare o desempenho dessas três abordagens:

N	python	entorpecido	pitão	tensorflow
2000	4.03	0,083	1.11	0,205
10.000	99	2,82	2,18	7,9

Cálculos vetorizados dão um ganho de mais de uma ordem decimal e meia em relação ao código python puro. A "placa da caldeira" em pytorch é visível: cálculos de pequenos volumes levam uma quantidade notável de tempo, mas quase não muda com o aumento do volume de cálculos.

Visualização

Atualmente, os dados podem ser visualizados usando um grande número de pacotes, como Matlab, Wolfram Mathematica, Maple, Matplotlib, etc. etc. Nesses pacotes, existem muitas funções complexas que fazem coisas complexas. Infelizmente, se você enfrentar uma tarefa simples, mas não padronizada, ficará desarmado. Minha solução favorita nessa situação é o povray. Este é um programa muito poderoso que geralmente é usado para criar imagens fotorrealistas, mas pode ser usado como um "montador de visualização". Normalmente, não importa o quão difícil seja a superfície que você deseja exibir, basta pedir ao povray para desenhar esferas com centros sobre essa superfície.

Usando a biblioteca vapory, você pode criar uma cena de povray diretamente em python, renderizá-la e ver o resultado. Agora fica assim:

A imagem é obtida da seguinte forma:

 import vapory from PIL import Image def create_scene(moment): angle = 2 * math.pi * moment / 360 r_camera = 7 camera = vapory.Camera('location', [r_camera * math.cos(angle), 1.5, r_camera * math.sin(angle)], 'look_at', [0, 0, 0], 'angle', 30) light1 = vapory.LightSource([2, 4, -3], 'color', [1, 1, 1]) light2 = vapory.LightSource([2, 4, 3], 'color', [1, 1, 1]) plane = vapory.Plane([0, 1, 0], -1, vapory.Pigment('color', [1, 1, 1])) box = vapory.Box([0, 0, 0], [1, 1, 1], vapory.Pigment('Col_Glass_Clear'), vapory.Finish('F_Glass9'), vapory.Interior('I_Glass1')) spheres = [vapory.Sphere( [float(r[0]), float(r[1]), float(r[2])], 0.05, vapory.Texture(vapory.Pigment('color', [1, 1, 0]))) for r in x] return vapory.Scene(camera, objects=[light1, light2, plane, box] + spheres, included=['glass.inc']) for t in range(0, 360): flnm = 'out/sphere_{:03}.png'.format(t) scene = create_scene(t) scene.render(flnm, width=800, height=600, remove_temp=False) clear_output() display(Image.open(flnm)) 

De vários arquivos, os gifs animados são montados usando o ImageMagic:

 convert -delay 10 -loop 0 sphere_*.png sphere_all.gif 

No github, você pode ver o código de funcionamento, cujos fragmentos são dados aqui. No segundo artigo, falarei sobre como começar a minimizar o funcional para que os pontos saiam do cubo e se espalhem uniformemente pela esfera.