Há várias tarefas nas quais o intervalo de valores de saída deve ser limitado, enquanto os dados de entrada não podem garantir isso. Além de situações forçadas, a limitação do sinal pode ser uma tarefa orientada a objetivos, por exemplo, ao compactar um sinal ou implementar o efeito "overdrive".
A implementação mais simples de uma restrição é forçá-la a um determinado valor se um determinado nível for excedido. Por exemplo, para um sinusóide com amplitude crescente, será assim:

Aqui, a função Clip atua como um limitador, como um argumento do qual o sinal de entrada e os parâmetros de restrição são transmitidos, e o resultado da função é o sinal de saída.
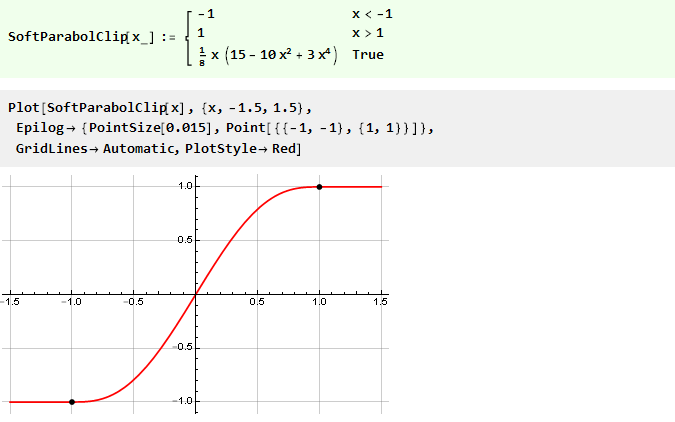
Vejamos o gráfico da função de clipe separadamente:
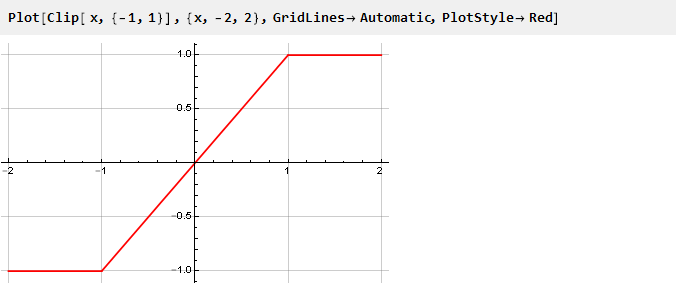
Pode-se ver que, embora não excedamos os limites do limite, o valor da saída é igual à entrada e o sinal não muda; quando excedido, o valor de saída não depende da entrada de forma alguma e permanece no mesmo nível. De fato, temos uma função contínua composta por três outras: y = -1, y = xey = 1, selecionada dependendo do argumento e equivalente à seguinte notação:

A transição entre funções ocorre abruptamente; e parece tentador torná-lo mais suave. Matematicamente, essa nitidez se deve ao fato de que as derivadas das funções nos pontos de ancoragem não coincidem. É fácil ver isso plotando a derivada da função Clip:
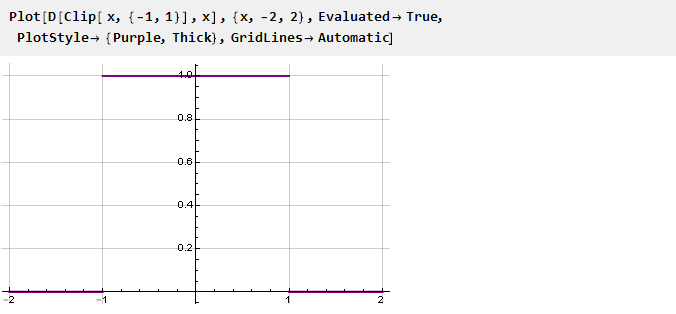
Assim, para garantir a suavidade da função de restrição, é necessário garantir a igualdade de derivadas nos pontos de união. E como as funções extremas que temos são constantes, cujas derivadas são iguais a zero, as funções de restrição derivadas nos pontos de ancoragem também devem ser iguais a zero. A seguir, consideraremos várias dessas funções que garantem o encaixe suave.
Sinus
O mais simples é usar a função sin no intervalo de -pi / 2 a pi / 2, cujas bordas os valores da derivada são iguais a zero por definição:
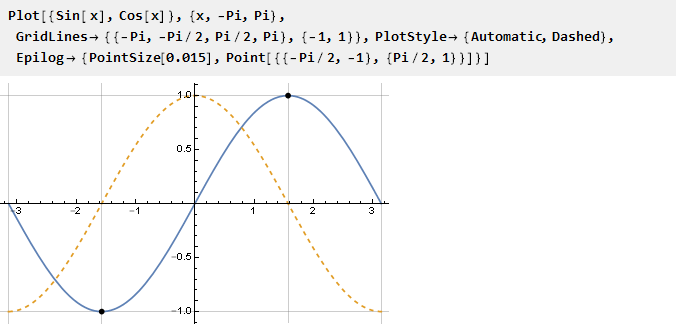
Você só precisa escalar os argumentos para que a unidade seja projetada no Pi / 2. Agora podemos definir a própria função delimitadora:

E construa sua agenda:
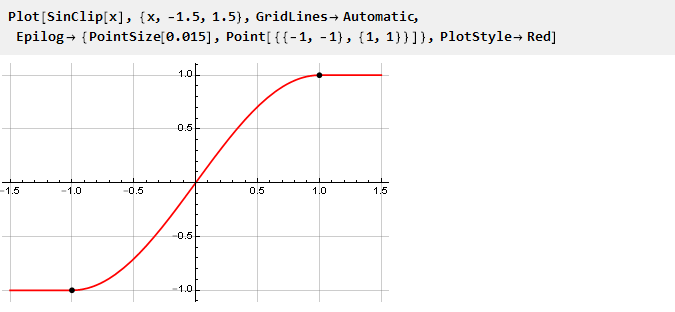
Como os limites de nossa restrição são estritamente definidos, a restrição é definida ao escalar o sinal de entrada com posterior (se necessário) retrocesso.
Também não há mais uma situação em que o sinal de entrada é transmitido para a saída sem distorção - quanto menor o nível de ganho, menor o nível de distorção devido à limitação - mas o sinal é distorcido em qualquer caso.
O efeito do parâmetro de ganho na distorção do sinal também pode ser visto na dinâmica:

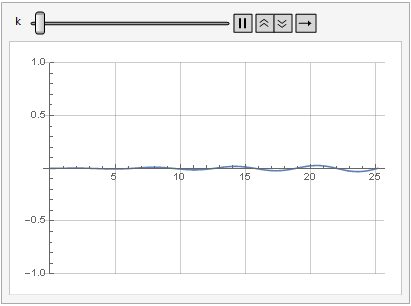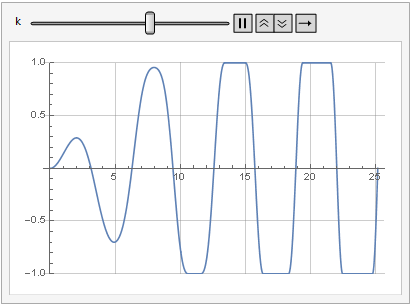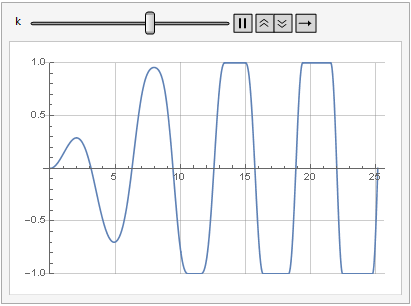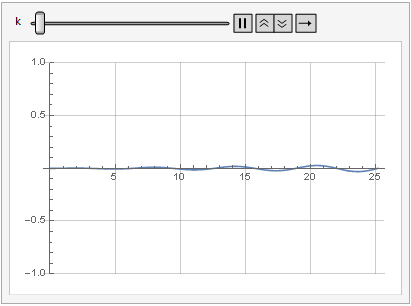
Mais suavidade
Vejamos a derivada de nossa função:
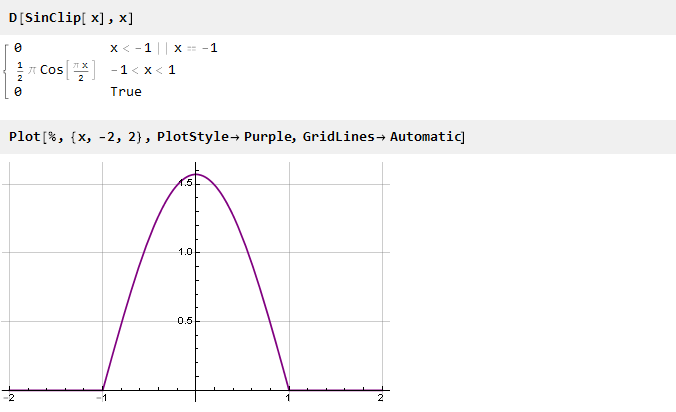
Ele não possui mais lacunas nos valores, mas há lacunas na derivada (a segunda, se contarmos com a função original). Para eliminá-lo, você pode seguir o caminho oposto - primeiro forme uma derivada suave e depois integre-a para obter a função desejada.
A maneira mais fácil de anular a derivada nos pontos -1 e 1 é simplesmente quadrar a função - todos os valores negativos da função se tornarão positivos e, consequentemente, ocorrerão inflexões nos pontos de interseção da função com zero.
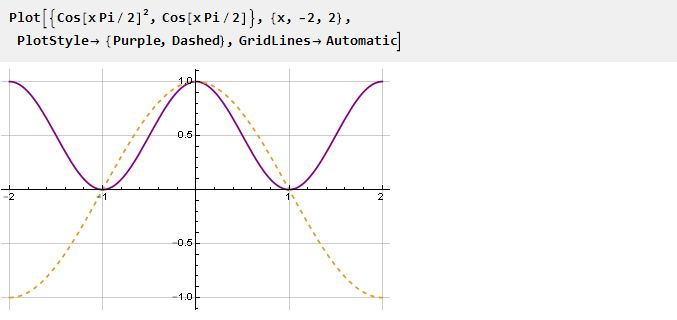
Encontre a antiderivada:
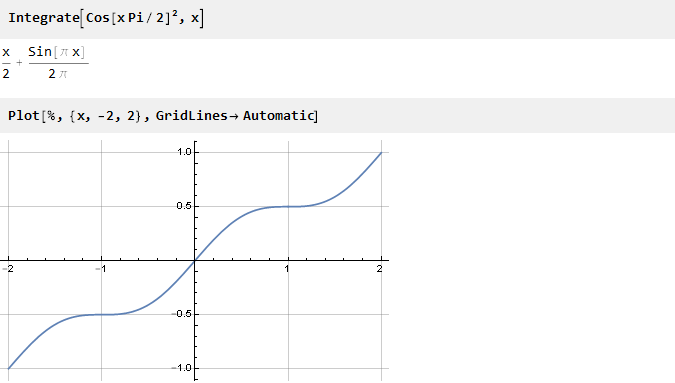
Agora resta escalá-lo ao longo do eixo das ordenadas. Para fazer isso, encontre seu valor no ponto 1:

E divida por ele (sim, especificamente aqui é uma multiplicação elementar por 2, mas isso nem sempre acontece):

Assim, a função de restrição final assumirá a forma:
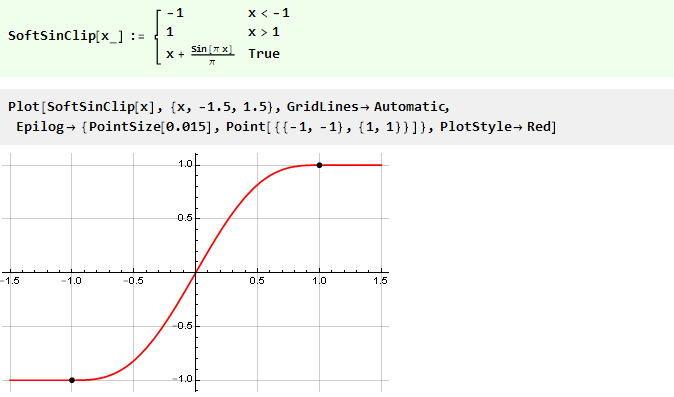
Passamos para polinômios
O uso de funções trigonométricas em alguns casos pode ser um pouco inútil. Portanto, tentaremos construir a função de que precisamos, permanecendo dentro da estrutura de operações matemáticas elementares.
Considere a parábola:
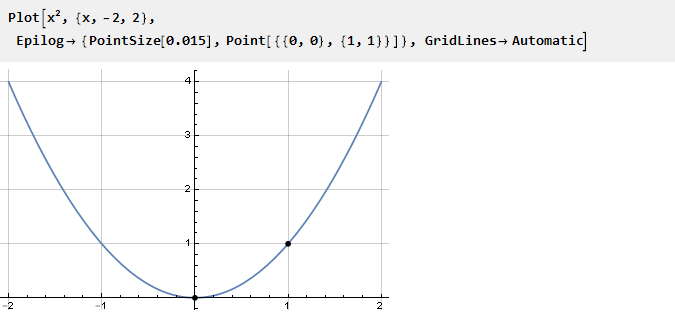
Como ele já possui uma inflexão no ponto zero, podemos usar a mesma parte no intervalo {0,1} para ancorar com constantes. Para valores negativos, ele precisa ser deslocado para baixo e para a esquerda:

e para positivo - refletem vertical e horizontalmente:

E nossa função com uma parábola assumirá a forma:
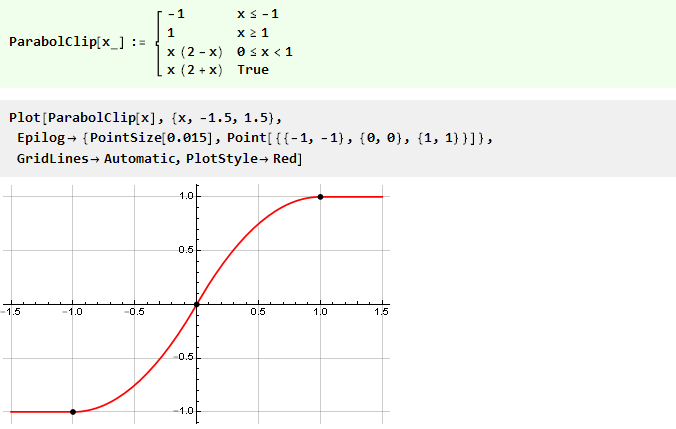
Vamos complicar um pouco
Vamos voltar à nossa parábola, virar e mudar uma unidade:
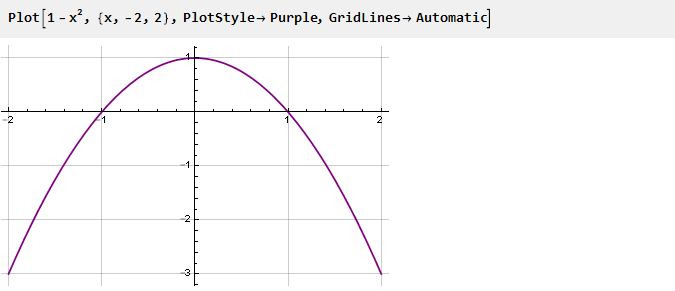
Isso será um derivado de nossa função. Para torná-lo mais suave nos pontos de junção, colocaremos o quadrado, zerando a segunda derivada desta maneira:
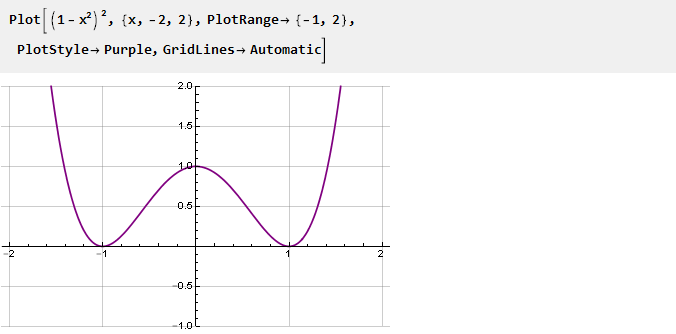
Integrar e escalar:

Temos uma função ainda mais suave:
Mais suavidade para o deus da suavidade
Aqui tentamos obter suavidade nos pontos de ancoragem em derivadas ainda mais altas. Para fazer isso, para começar, definimos a função como um polinômio com coeficientes desconhecidos e tentamos encontrar os coeficientes através de uma solução do sistema de equações.
Vamos começar com a primeira derivada:

2º:

3º:

Todos esses coeficientes parecem ter algum tipo de lógica. Escrevemos os fatores, multiplicando-os pelo valor do grau em x; e para não escrever sempre a mesma coisa, automatizamos o processo de encontrar os coeficientes:
 Parece
Parece coeficientes binomiais. Fazemos uma suposição ousada de que são e, com base nisso, escrevemos a fórmula generalizada:

Verifique:
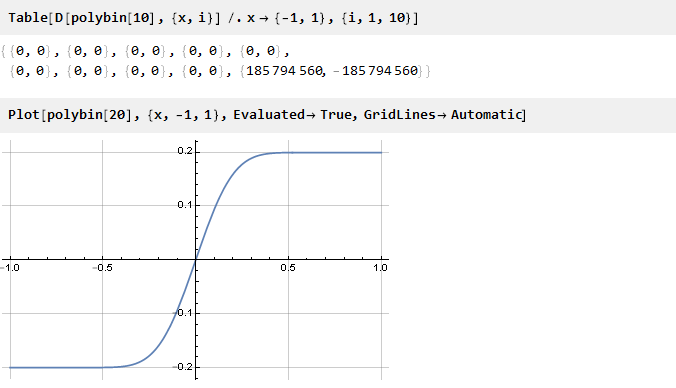
Parece ser verdade
[1] . Resta apenas calcular o fator de escala para unir as arestas:

E depois de escalar e simplificar, descobrimos que nosso conhecimento de matemática está um pouco desatualizado
[2] :
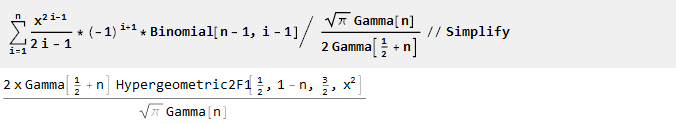
Assim, obtivemos uma função geradora de ordem n na qual n-1 das primeiras derivadas são iguais a zero:

Vamos ver o que aconteceu:
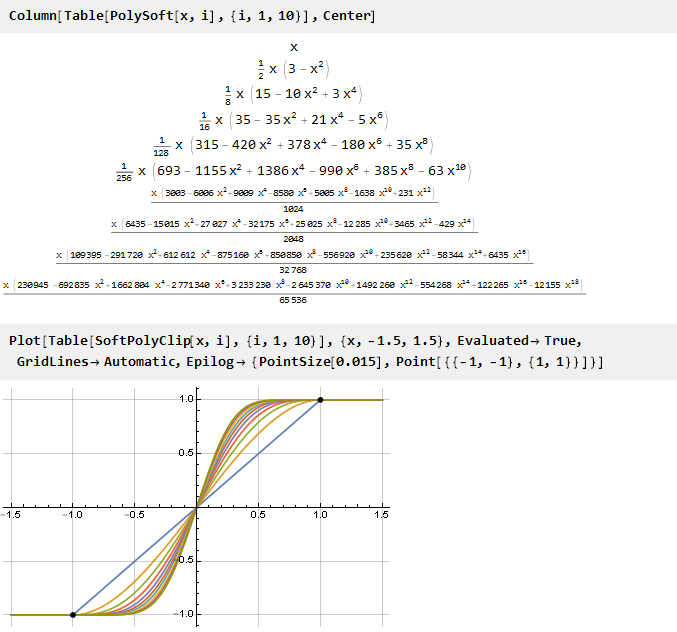
E como nossa fórmula generalizada acabou sendo contínua, você pode usar valores de parâmetro não inteiro, se desejar:
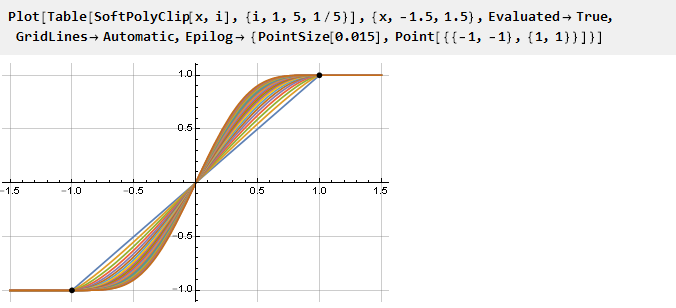
Você também pode criar gráficos de derivativos reduzidos a uma escala:
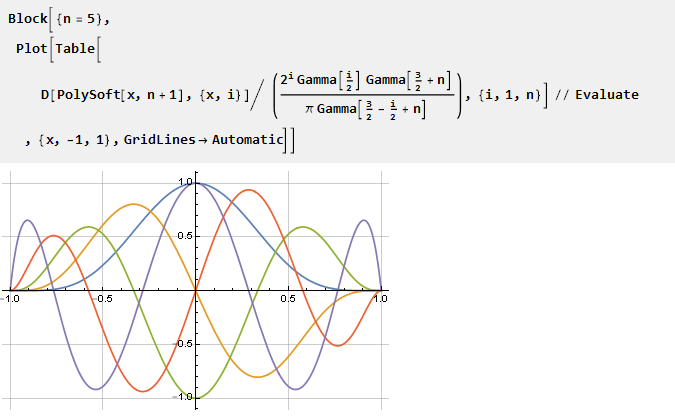
Adicione rigidez
Seria tentador ser capaz de ajustar o grau de "rigidez" da restrição.
Vamos voltar à nossa parábola invertida e adicionar um coeficiente no grau x:

Quanto maior n, maior nossa derivada é "quadrada" e sua antiderivada é acentuada, respectivamente:
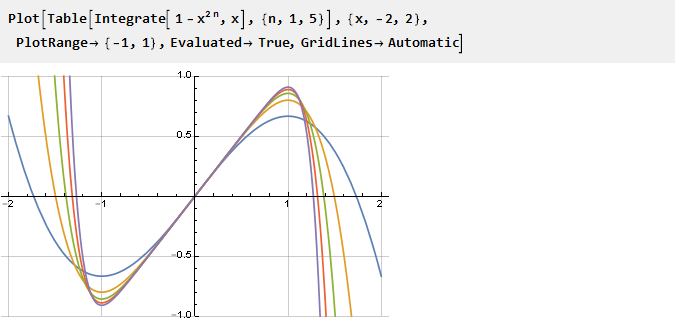
Calculamos a antiderivada e ajustamos a escala:

Agora vamos tentar definir a etapa fracionária para o parâmetro:
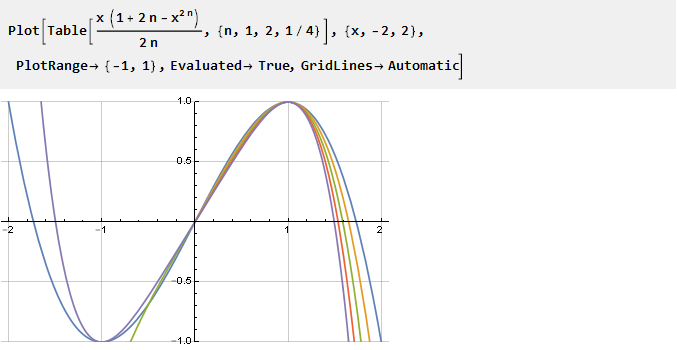
Como você pode ver, nem todos os n têm a solução correta na parte negativa, mas as condições necessárias para nós ainda são atendidas na parte correta (positiva) - portanto, para valores negativos, podemos simplesmente usá-la invertida com um argumento invertido. E como o domínio de definição do parâmetro não está mais limitado apenas a números inteiros positivos, podemos simplificar a fórmula substituindo 2n por n:

E substituindo n por n-1, você pode tornar a fórmula um pouco mais bonita:
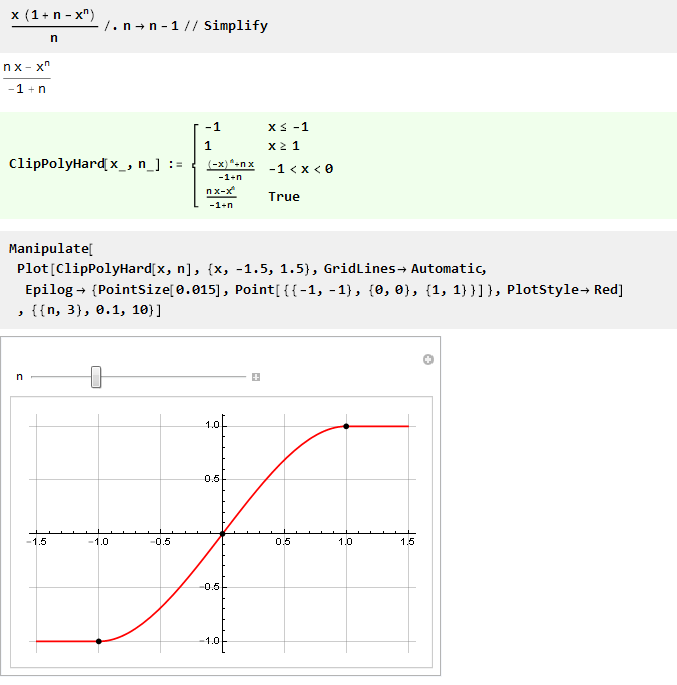
Como para n igual a um, obtemos a divisão por zero, e tente encontrar o limite:

O limite é encontrado, o que significa que agora podemos adicionar
[3] a função para n a 1 e considerá-la para todos os n zeros grandes:
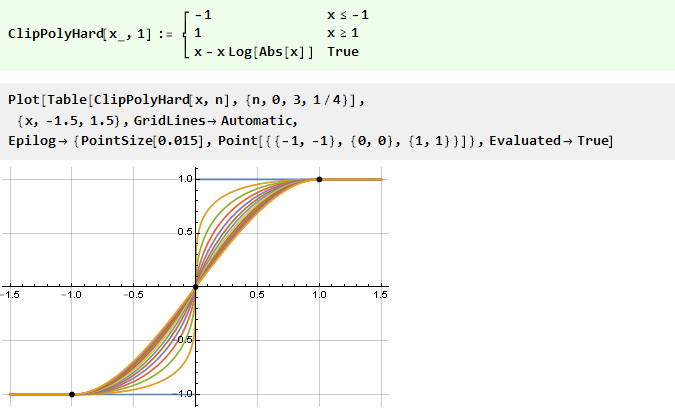
Se inicialmente equipararmos nossa parábola invertida, obteremos uma função ainda mais suave:
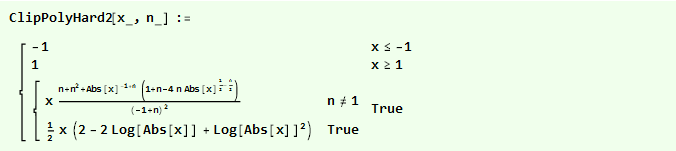
E podemos compará-los em um gráfico:
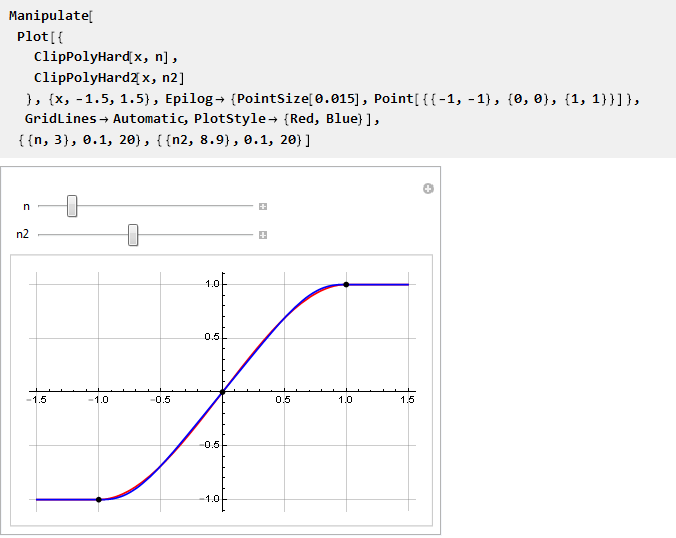
Simplifique
Vejamos a seguinte função:
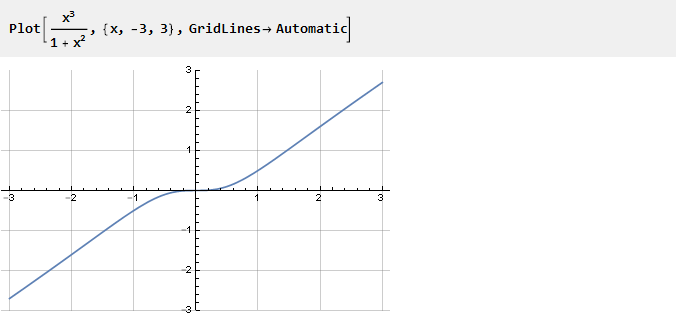
Ela não apareceu por acaso.
Se você remover uma unidade dela, x
2 se contrairá e apenas x permanecerá, ou seja, uma linha inclinada. Assim, quanto menor o valor de x, maior a influência da unidade no denominador, criando a curvatura de que precisamos. E considerando esta função em diferentes escalas, você pode controlar o grau dessa curvatura:

Assim, podemos reescrever a função anterior com controle de rigidez usando apenas um polinômio racional de 3 ordens:
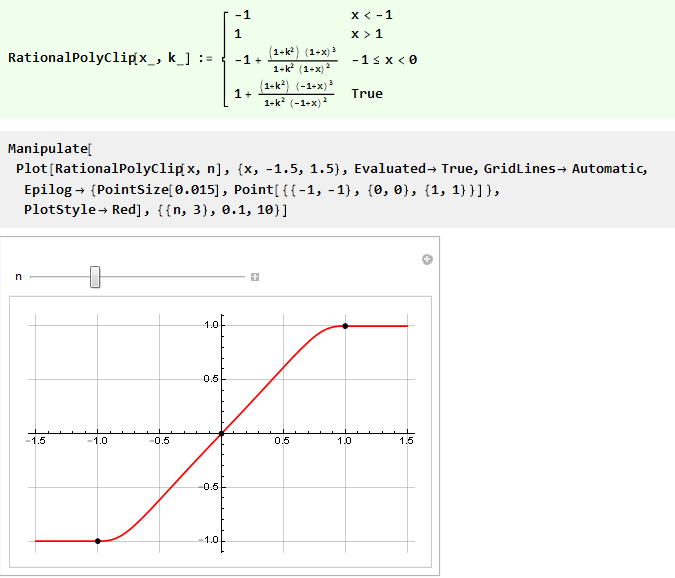
Automatize
Para não especificar funções contínuas por partes de cada vez, podemos definir uma função auxiliar que fará isso por conta própria, assumindo uma função doadora como argumento como entrada.
Se nossa função já possui simetria diagonal e está alinhada ao centro de coordenadas (como uma onda senoidal), então podemos simplesmente fazer
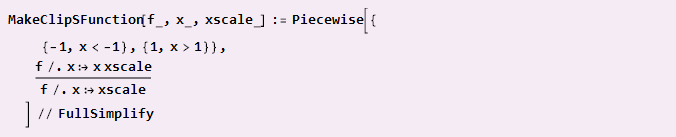
Exemplo de uso:

Se você precisar montar a partir de peças, como no caso de uma parábola, e o centro de coordenadas determinar os pontos de ancoragem, a fórmula será um pouco mais complicada:
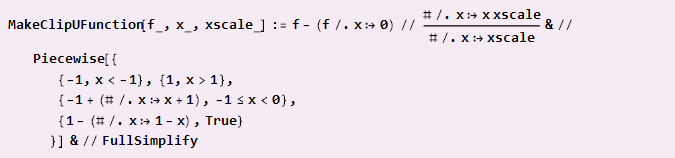
Exemplo de uso:

Vamos para o expositor
Absolutamente qualquer função pode ser um doador para resolver esse problema, você só precisa fornecer pontos de inflexão. Tomemos, por exemplo, o expoente reduzido em um:
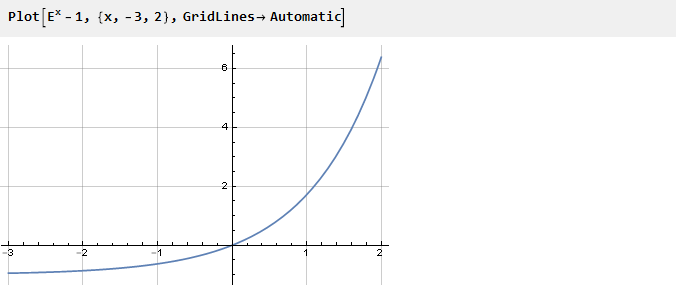
Anteriormente, para garantir a inflexão necessária no ponto zero, ajustamos a função ao quadrado. Mas você pode seguir o outro caminho - por exemplo, resumir com outra função cuja derivada no ponto zero é um sinal oposto à derivada do expoente. Por exemplo, -x:
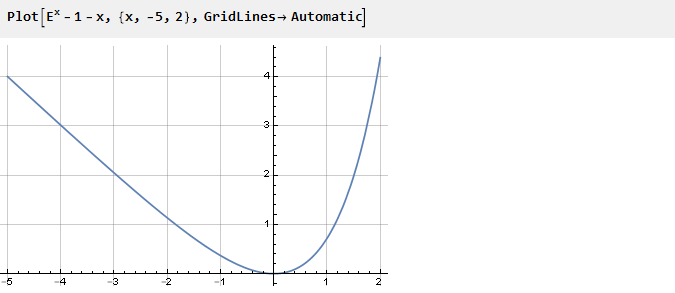
Dependendo de que lado tomaremos a curva, a forma final da função dependerá dela. Agora, usando a função auxiliar definida anteriormente e escolhendo um dos lados, obtemos:

Ou

E agora podemos compará-los em um gráfico:
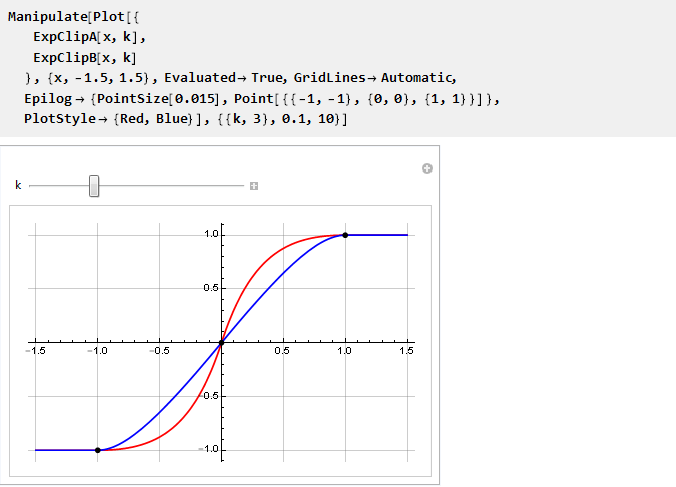
É visto que, como k → 0, eles tendem a coincidir; e como não podemos calcular diretamente seus valores, como obtemos a divisão por zero, usaremos o limite:

E eles obtiveram a função por partes da parábola já conhecida por nós.
Quebrando simetria
Até agora, estamos considerando funções exclusivamente simétricas. No entanto, há momentos em que não precisamos de simetria - por exemplo, para simular distorções no som dos amplificadores valvulados.
Pegue o expoente e multiplique-o por uma parábola invertida ao quadrado - para obter a interseção com o eixo da abcissa nos pontos -1 e 1 e, ao mesmo tempo, garantir a suavidade da segunda derivada; a parametrização é possível através do dimensionamento do argumento expoente:
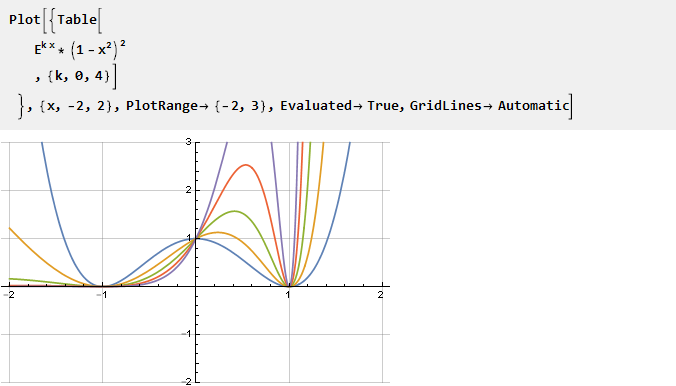
Encontre a antiderivada e dimensione-a:
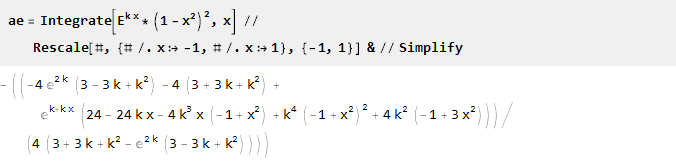
Como para k = 0, obtemos a divisão por zero:

Além disso, encontramos o limite,

que é um polinômio suave de terceira ordem já conhecido por nós. Combinando tudo em uma função, obtemos
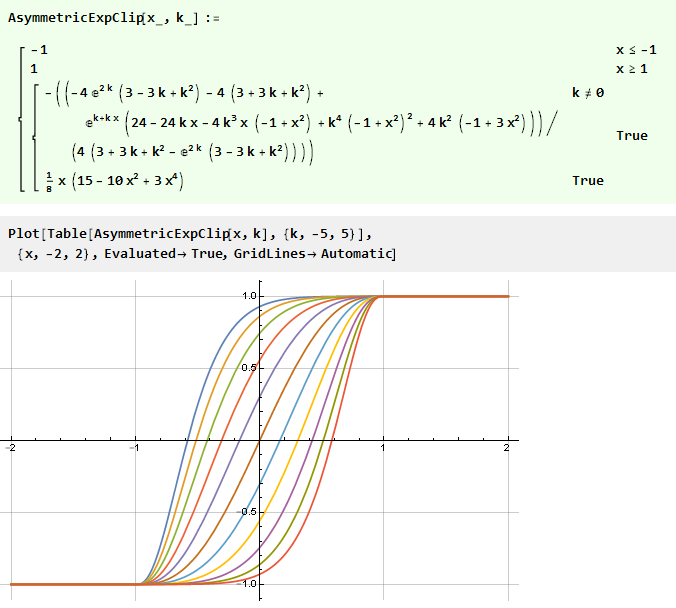
Em vez de projetar inicialmente uma função assimétrica, você pode ir para o outro lado - use a simétrica pronta, mas "dobre" o valor dessa função usando uma função de curva adicional definida no intervalo {-1,1}.
Considere, por exemplo, uma hipérbole:
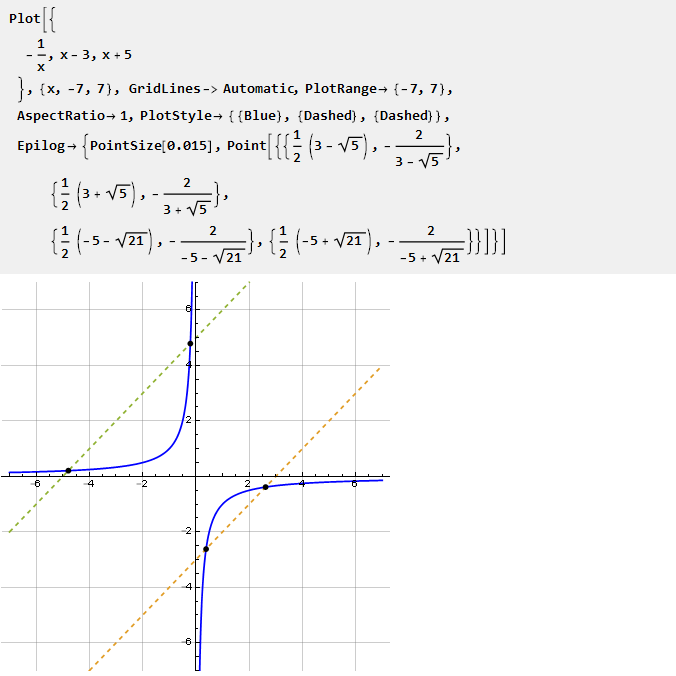
Considerando seu segmento em diferentes escalas, você pode ajustar o grau de curvatura nas duas direções. Como encontrar este segmento? Com base no gráfico, pode-se procurar a interseção da hipérbole com a linha. No entanto, como esse cruzamento nem sempre existe, isso cria algumas dificuldades. Portanto, iremos para o outro lado.
Primeiro, adicione fatores de escala à hipérbole:

então, comporemos um sistema de equações que define as condições para a passagem de uma hipérbole através de determinados pontos - e sua solução fornecerá os coeficientes de interesse para nós:

Agora substitua a solução na fórmula original e simplifique:

Vamos ver o que obtemos, dependendo do parâmetro k:
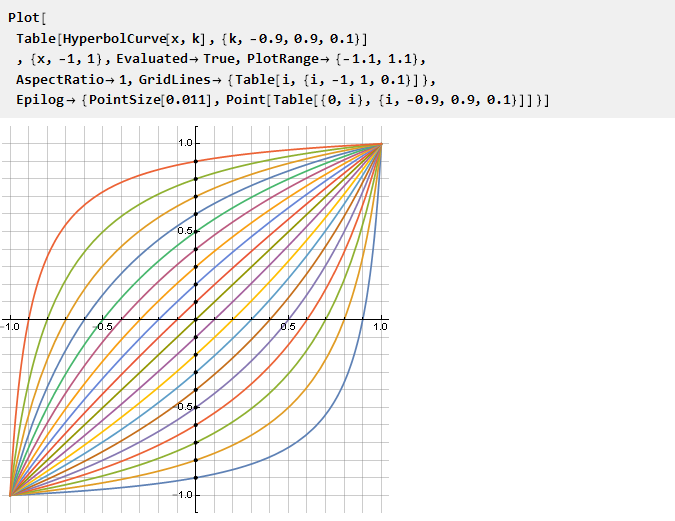
Vale ressaltar que para k = 0 a fórmula entra em colapso naturalmente em x e nenhuma situação especial ocorre - embora, com referência ao hipérbole inicial, isso seja equivalente a um segmento de comprimento zero e dois de uma vez. Não é menos notável que a função inversa seja a mesma, mas com um parâmetro negativo k:

Agora podemos usá-lo para modificar uma função de restrição arbitrária, e o parâmetro k define o ponto de interseção com o eixo de ordenadas:
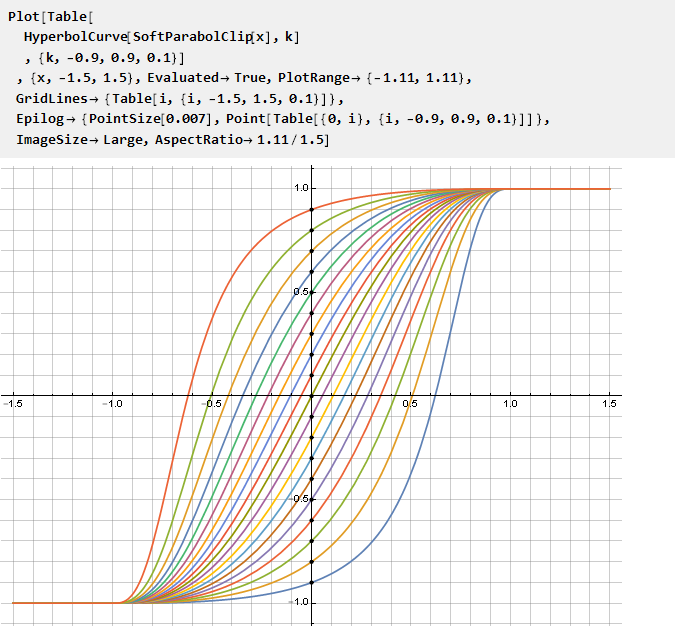
Da mesma forma, você pode construir curvas a partir de outras funções, por exemplo, uma lei de energia com uma base variável:
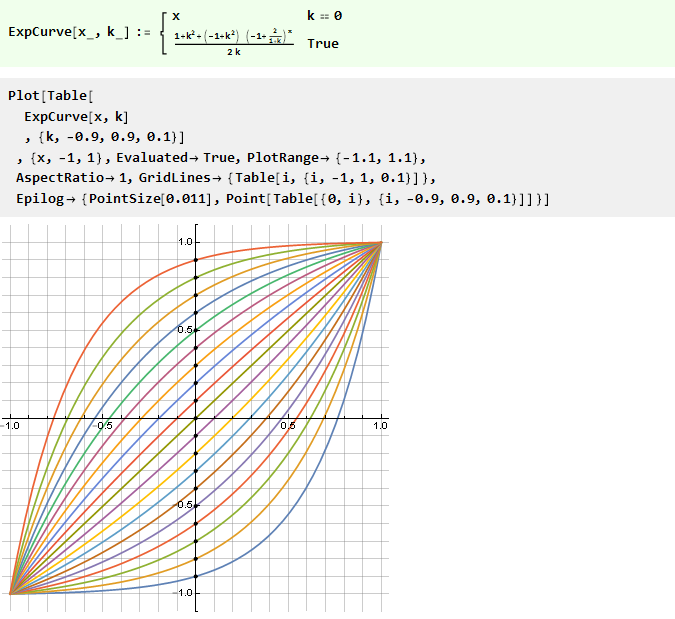
Ou o inverso disso é logarítmico:
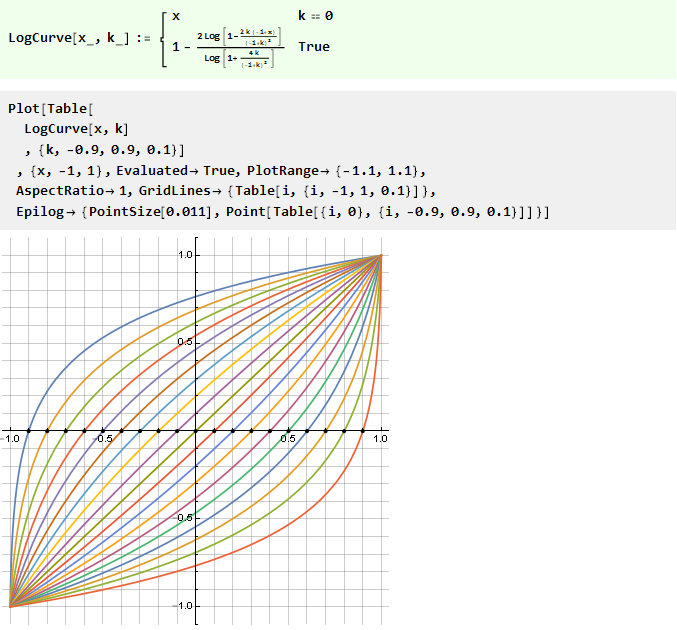
Precisa de mais precisão
Podemos querer ter um espaçamento linear garantido para uma função em um determinado intervalo. Isso é lógico para organizar, introduzindo uma linha reta em uma função contínua por partes,
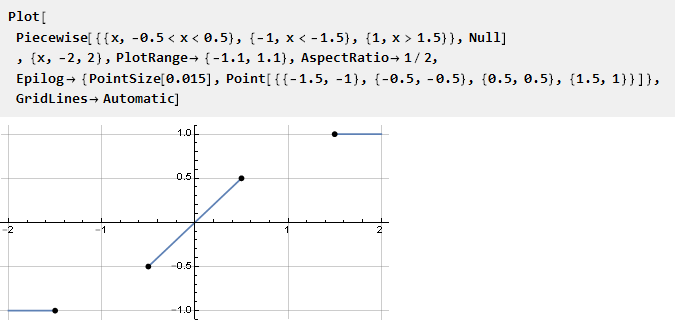
espaços vazios nos quais você precisa preencher alguma função. Obviamente, para um encaixe suave com uma seção linear, sua primeira derivada deve ser igual à unidade; e todo o subsequente (se possível) zero. Para não deduzir tal função novamente, podemos pegar uma pronta e adaptá-la para esta tarefa. Você também pode notar que os pontos extremos estão localizados um pouco além da unidade - isso é necessário para manter a inclinação da seção linear.
Pegue a função PolySoft derivada anteriormente e altere-a para obter uma no centro de coordenadas:
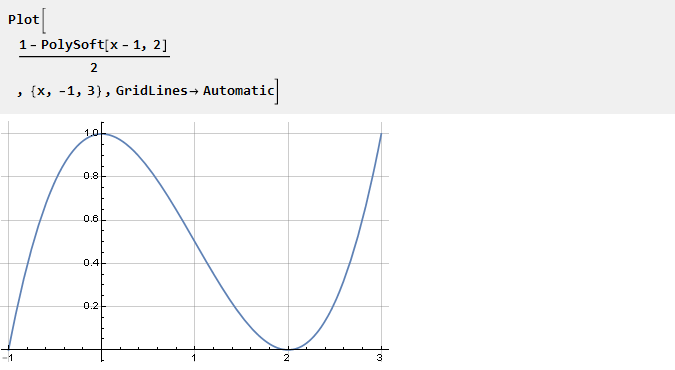
A partir de suas propriedades, segue-se que n-1 dos derivados subsequentes nos pontos 0 e 2 será igual a zero:
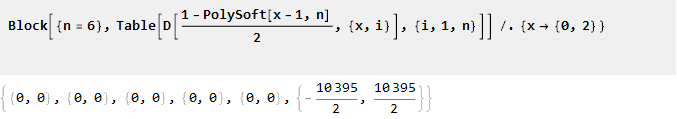
Agora integre-o:
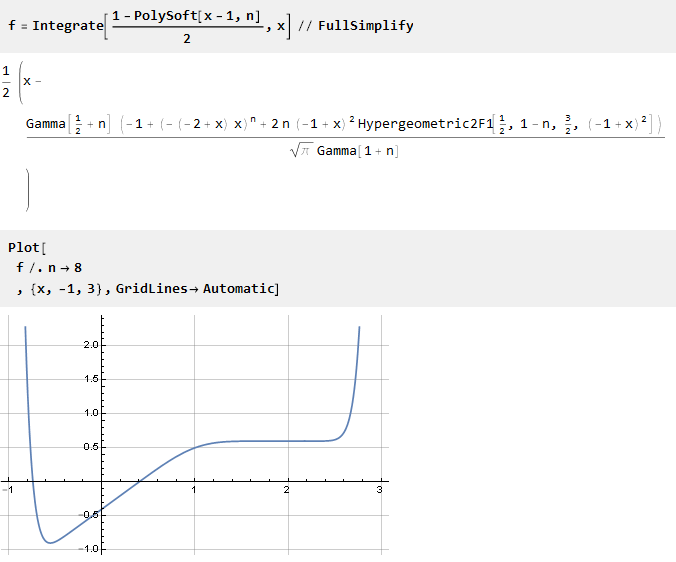
A função foi deslocada para baixo em relação ao eixo da abcissa. Portanto, é necessário adicionar uma constante (igual ao valor da função no ponto 0) para combinar os centros de coordenadas:

Aqui temos zero no grau n. Não declinou, pois o valor de zero no grau de zero não está definido; podemos excluí-lo manualmente ou, simplificando, podemos indicar explicitamente que n é maior que zero:

Vamos verificar por precaução. O valor nos pontos 0 e 2 para todos os n:

Derivadas nas bordas do intervalo (para um polinômio de ordem 5):

Como você pode ver, a função acabou sendo bastante complicada. Para não arrastá-lo e não complicar os cálculos, continuaremos manipulando com um polinômio específico, por exemplo, quarta ordem:

E agora, com ele, você pode preencher o espaço livre:

Verifique:
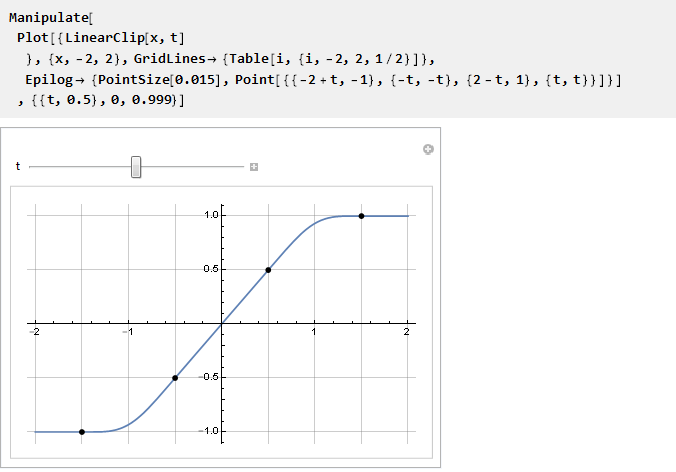
Vamos para o infinito
Às vezes, pode haver uma necessidade de funções que tendem a uma unidade, mas não a alcançam. A Wikipedia
sugere várias soluções conhecidas:
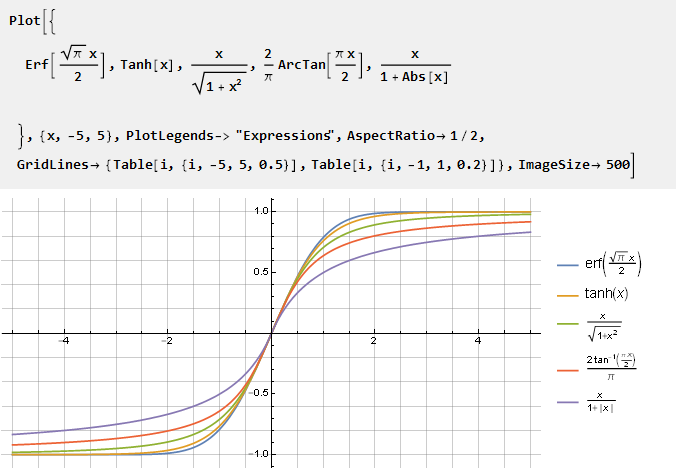
Como essas funções não alcançam a unidade, é mais conveniente normalizá-las com relação à derivada no centro de coordenadas.
Podemos modificar a forma de tais funções através de seus argumentos usando alguma função diagonal-simétrica, por exemplo:
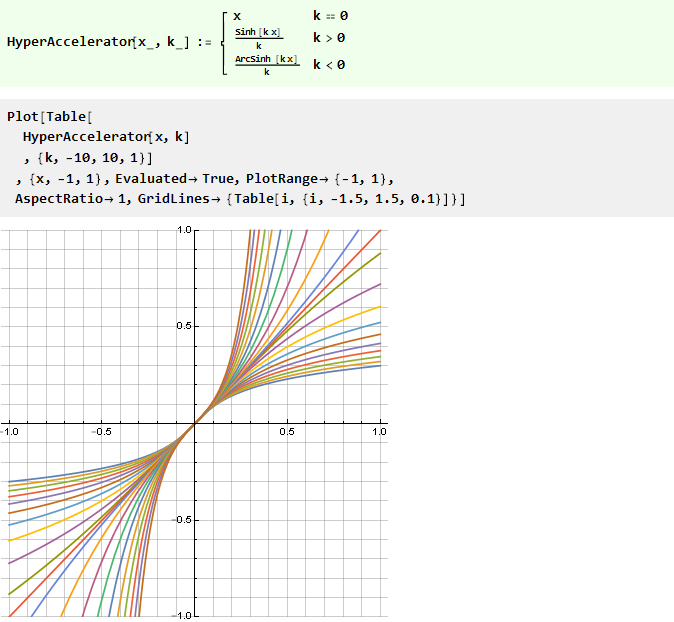
Essa função, a propósito, também é inversa a si mesma, ou seja,
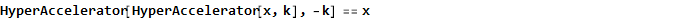
E, como aplicado ao arco tangente, como exemplo, obtemos
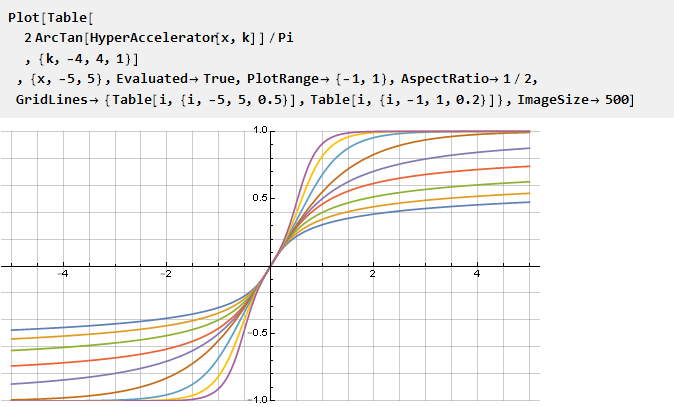
que, em particular, com o parâmetro k = 1 nos dará
a função Guderman .
Como você pode ver, com essa abordagem, torções indesejáveis podem ser obtidas, portanto, é mais preferível controlar a rigidez da restrição diretamente através da propriedade da própria função. Considere várias dessas funções com um parâmetro, cuja saída é omitida por questões de brevidade.
A partir da função de energia:
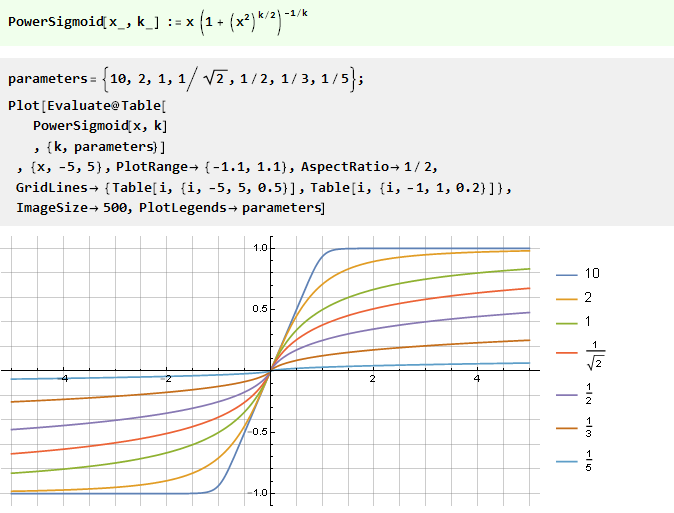
Da soma de duas funções em forma de V com um deslocamento:
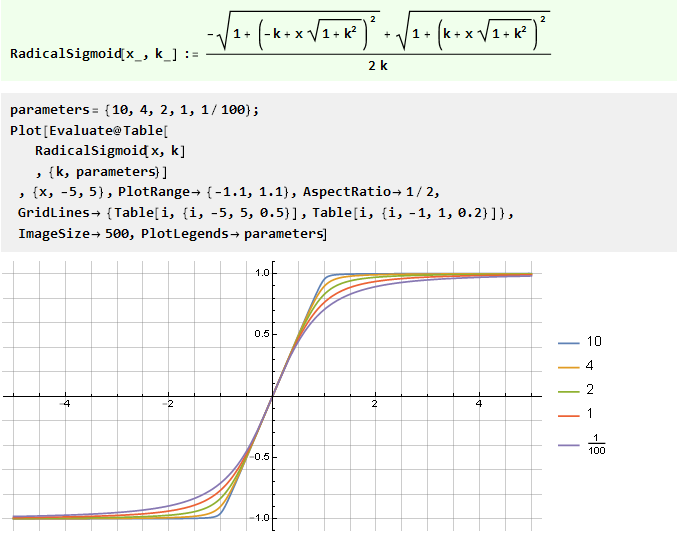
Na função de erro generalizado:
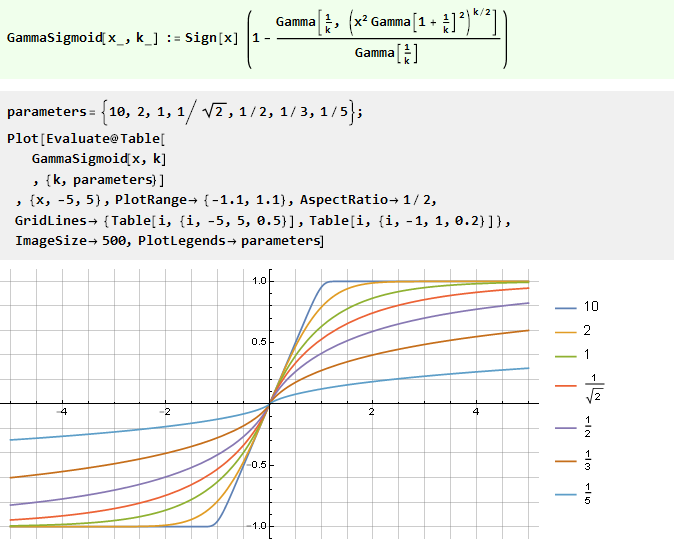
Integração de um polinômio racional:
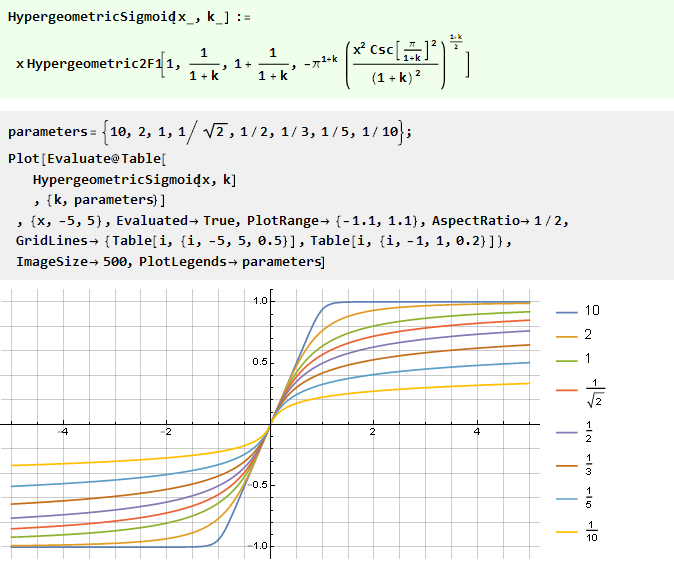
Curiosamente, o seu caso especial é arctangente:

Conclusão
A construção de tais funções pode ser uma tarefa fascinante, durante a qual serão obtidas fórmulas simples e complexas, belas e não muito. Pode parecer que eles são todos muito parecidos entre si e não há necessidade de tal variedade. Este não é necessariamente o caso.
A diferença pode ser mais visível em outras escalas - por exemplo, logarítmica. Além disso, além das tarefas indicadas no cabeçalho, funções semelhantes também podem ser usadas em outras tarefas - misturar sinais, quando a atenuação suave de um sinal é combinada com o aumento suave de outro, ou a construção de filtros acústicos - e então a diferença será percebida pelo ouvido ou para criar gradientes - e então a diferença será percebida pelo olho. Além disso, eles também podem ser usados como doadores para outras funções mais complexas - por exemplo,
janela .
Em conclusão, vale esclarecer mais alguns pontos.
Todas as funções aqui foram definidas no intervalo de -1 a 1. Se você precisar de um intervalo diferente (por exemplo, de 0 a 1), ele poderá ser facilmente recontado manualmente:
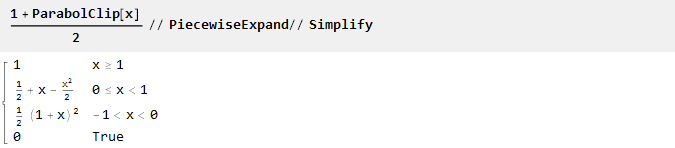
Ou usando a função de zoom embutida:

E para facilitar a exportação das fórmulas obtidas para o código do programa, a função CForm pode ser útil:
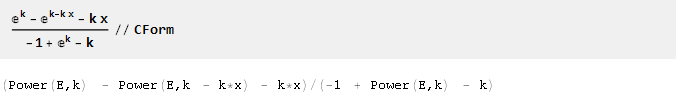
O documento fonte do Mathematica pode ser baixado
aqui .
Notas:
[1] Um verdadeiro matemático certamente será capaz de provar rigorosamente (ou refutar) essa afirmação.
[2] funções hipergeométricas não são consideradas no curso padrão da análise matemática.
[3] essa sobrecarga é definida apenas para uma unidade de caracteres; uma unidade em formato de ponto flutuante (por exemplo, ao plotar um gráfico) não será reconhecida.