Oi habr.
O tema dos "quadrados mágicos" é bastante interessante, porque por um lado, são conhecidas desde a antiguidade; por outro, o cálculo do "quadrado mágico" até hoje é uma tarefa computacional muito difícil. Lembre-se de que, para construir um NxN de “quadrado mágico”, é necessário inserir os números 1..N * N para que a soma de suas horizontais, verticais e diagonais seja igual ao mesmo número. Se você simplesmente escolher o número de todas as opções para organizar os números de um quadrado 4x4, obteremos 16! = 20.922.789.888.000 opções.
Considere como isso pode ser feito com mais eficiência.

Para começar, repetimos a condição do problema. Você precisa organizar os números em um quadrado para que eles não se repitam, e a soma das horizontais, verticais e diagonais era igual ao mesmo número.
É fácil provar que essa soma é sempre a mesma e é calculada pela fórmula para qualquer n:
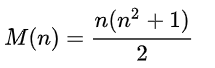
Vamos considerar quadrados 4x4, então a soma = 34.
Denote todas as variáveis por X, nosso quadrado ficará assim:
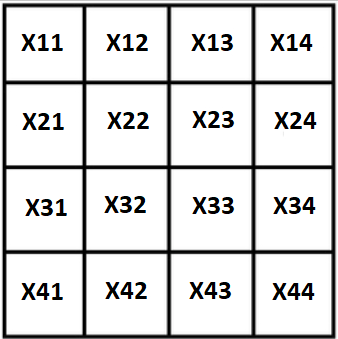
A primeira e óbvia propriedade: Se a soma do quadrado for conhecida, as rajadas extremas podem ser expressas pelos 3 restantes:
X14 = S - X11 - X12 - X13
X24 = S - X21 - X22 - X23
...
X41 = S - X11 - X21 - X31Assim, um quadrado 4x4 na verdade se transforma em um quadrado 3x3, o que reduz o número de opções de pesquisa de 16! até 9! 57 milhões de vezes. Sabendo disso, começamos a escrever código, ver o quão complicada é a busca exaustiva por computadores modernos.
C ++ - versão de thread único
O princípio do programa é muito simples. Pegamos o conjunto de números 1..16 e o loop for sobre esse conjunto, será x11. Em seguida, pegamos o segundo conjunto, consistindo no primeiro, com exceção do número x11, e assim por diante.
Uma forma aproximada do programa é semelhante a esta:
int squares = 0; int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); for (int x11 = 1; x11 <= MAX; x11++) { Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; ... int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue;
O texto completo do programa pode ser encontrado no spoiler.
Fonte inteira #include <set> #include <stdio.h> #include <ctime> #include "stdafx.h" typedef std::set<int> Set; typedef Set::iterator SetIterator; #define N 4 #define MAX (N*N) #define S 34 int main(int argc, char *argv[]) { // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 const clock_t begin_time = clock(); int squares = 0; int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); for (int x11 = 1; x11 <= MAX; x11++) { Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; Set set21(set13); set21.erase(x13); set21.erase(x14); for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++) { int x21 = *it21; Set set22(set21); set22.erase(x21); for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++) { int x22 = *it22; Set set23(set22); set23.erase(x22); for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++) { int x23 = *it23, x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; Set set31(set23); set31.erase(x23); set31.erase(x24); for (SetIterator it31 = set31.begin(); it31 != set31.end(); it31++) { int x31 = *it31; Set set32(set31); set32.erase(x31); for (SetIterator it32 = set32.begin(); it32 != set32.end(); it32++) { int x32 = *it32; Set set33(set32); set33.erase(x32); for (SetIterator it33 = set33.begin(); it33 != set33.end(); it33++) { int x33 = *it33, x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x41 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); squares++; } } } } } } } } } printf("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); return 0; }
Resultado: foram encontradas
7040 opções de quadrados mágicos 4x4 e o tempo de pesquisa foi de
102s .

A propósito, é interessante verificar se a lista de quadrados contém a mesma que está representada na gravura de Durer. Claro que sim, porque o programa exibe
todos os quadrados 4x4:
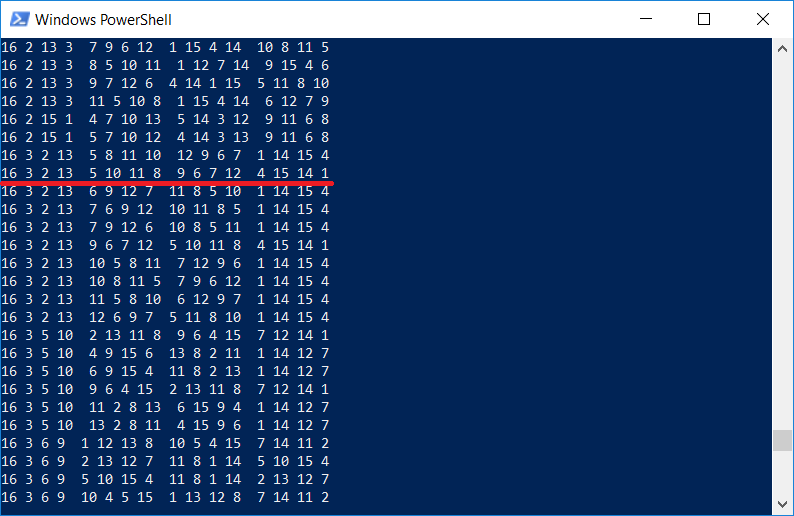
Note-se que Dürer inseriu um quadrado na imagem por uma razão, os números
1514 também indicam o ano da gravação.
Como você pode ver, o programa funciona (marcamos a tarefa como verificada em 1514 por Albrecht Dürer;), mas o tempo de execução não é tão pequeno para um computador com um processador Core i7. Obviamente, o programa é executado em um único thread, e é aconselhável usar todos os outros kernels.
C ++ - versão multithread
Reescrever um programa usando fluxos é basicamente simples, embora um pouco complicado. Felizmente, hoje existe uma opção quase esquecida - o uso do suporte ao
OpenMP (Open Multi-Processing). Essa tecnologia existe desde 1998 e permite que as diretivas do processador digam ao compilador quais partes do programa serão executadas em paralelo. O OpenMP também é suportado no Visual Studio, portanto, para transformar um programa em multiencadeado, basta adicionar uma linha ao código:
int squares = 0; #pragma omp parallel for reduction(+: squares) for (int x11 = 1; x11 <= MAX; x11++) { ... } printf("CNT: %d\n", squares);
A
diretiva #pragma omp parallel for indica que o próximo loop for pode ser executado em paralelo, e o parâmetro adicional squares define o nome da variável, que será comum para threads paralelos (sem isso, o incremento não funcionará corretamente).
O resultado é óbvio: o tempo de execução foi reduzido de 102 para
18 .

Fonte inteira #include <set> #include <stdio.h> #include <ctime> #include "stdafx.h" typedef std::set<int> Set; typedef Set::iterator SetIterator; #define N 4 #define MAX (N*N) #define S 34 int main(int argc, char *argv[]) { // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 const clock_t begin_time = clock(); int squares = 0; #pragma omp parallel for reduction(+: squares) for (int x11 = 1; x11 <= MAX; x11++) { int digits[] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 }; Set mset(digits, digits + N*N); Set set12(mset); set12.erase(x11); for (SetIterator it12 = set12.begin(); it12 != set12.end(); it12++) { int x12 = *it12; Set set13(set12); set13.erase(x12); for (SetIterator it13 = set13.begin(); it13 != set13.end(); it13++) { int x13 = *it13; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) continue; if (x14 == x11 || x14 == x12 || x14 == x13) continue; Set set21(set13); set21.erase(x13); set21.erase(x14); for (SetIterator it21 = set21.begin(); it21 != set21.end(); it21++) { int x21 = *it21; Set set22(set21); set22.erase(x21); for (SetIterator it22 = set22.begin(); it22 != set22.end(); it22++) { int x22 = *it22; Set set23(set22); set23.erase(x22); for (SetIterator it23 = set23.begin(); it23 != set23.end(); it23++) { int x23 = *it23, x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; Set set31(set23); set31.erase(x23); set31.erase(x24); for (SetIterator it31 = set31.begin(); it31 != set31.end(); it31++) { int x31 = *it31; Set set32(set31); set32.erase(x31); for (SetIterator it32 = set32.begin(); it32 != set32.end(); it32++) { int x32 = *it32; Set set33(set32); set33.erase(x32); for (SetIterator it33 = set33.begin(); it33 != set33.end(); it33++) { int x33 = *it33, x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x41 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); squares++; } } } } } } } } } printf("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); return 0; }
Isso é muito melhor - porque Se a tarefa estiver quase perfeitamente paralelizada (os cálculos em cada ramificação são independentes), o tempo é menor que o número de vezes igual ao número de núcleos do processador. Mas, infelizmente, não
é possível obter muito mais desse código, embora alguns por cento possam e possam ser conquistados por algumas otimizações. Passamos para artilharia mais pesada, cálculos na GPU.
Computando com NVIDIA CUDA
Se você não entrar em detalhes, o processo de cálculo realizado na placa de vídeo pode ser representado como vários blocos de hardware paralelos (blocos), cada um dos quais executa vários processos (threads).
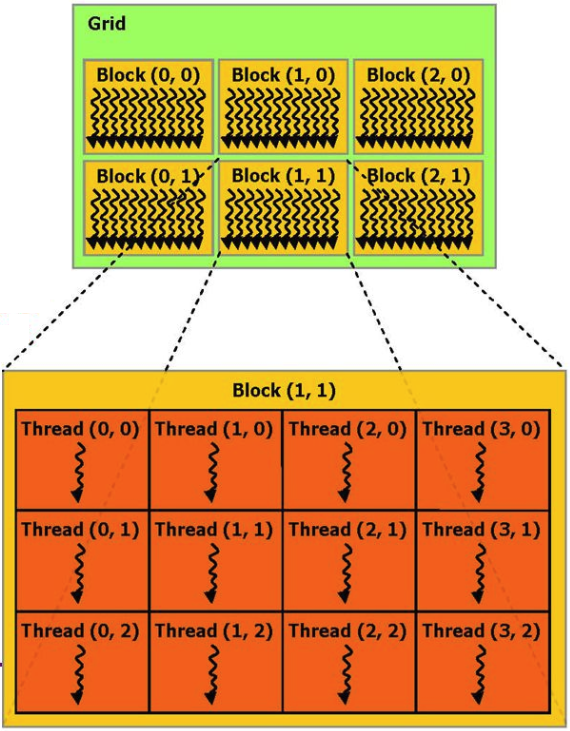
Por exemplo, podemos dar um exemplo da função de adicionar 2 vetores da documentação da CUDA:
__global__ void add(int n, float *x, float *y) { int index = threadIdx.x; int stride = blockDim.x; for (int i = index; i < n; i += stride) y[i] = x[i] + y[i]; }
As matrizes x e y são comuns para todos os blocos, e a própria função é executada simultaneamente em vários processadores ao mesmo tempo. A chave aqui é o paralelismo - os processadores de placa de vídeo são muito mais simples que uma CPU comum, mas existem muitos deles e eles estão focados especificamente no processamento de dados numéricos.
É disso que precisamos. Temos uma matriz de números X11, X12, .., X44. Vamos começar o processo de 16 blocos, cada um deles executando 16 processos. O número do bloco corresponderá ao número X11, o número do processo ao número X12 e o próprio código calculará todos os quadrados possíveis com os X11 e X12 selecionados. É simples, mas existe uma sutileza - os dados precisam não apenas ser calculados, mas também transferidos da placa de vídeo, para isso, armazenaremos o número de quadrados encontrados no elemento zero da matriz.
O código principal é muito simples:
#define N 4 #define SQ_MAX 8*1024 #define BLOCK_SIZE (SQ_MAX*N*N + 1) int main(int argc,char *argv[]) { const clock_t begin_time = clock(); int *results = (int*)malloc(BLOCK_SIZE*sizeof(int)); results[0] = 0; int *gpu_out = NULL; cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int)); cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice); squares<<<MAX, MAX>>>(gpu_out); cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost); // Print results int squares = results[0]; for(int p=0; p<SQ_MAX && p<squares; p++) { int i = MAX*p + 1; printf("[%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d]\n", results[i], results[i+1], results[i+2], results[i+3], results[i+4], results[i+5], results[i+6], results[i+7], results[i+8], results[i+9], results[i+10], results[i+11], results[i+12], results[i+13], results[i+14], results[i+15]); } printf ("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); cudaFree(gpu_out); free(results); return 0; }
Selecionamos o bloco de memória na placa de vídeo usando o cudaMalloc, executamos a função dos quadrados, indicando 2 parâmetros 16.16 (o número de blocos e o número de threads) correspondentes aos números 1..16 repetidos, depois copiamos os dados através do cudaMemcpy.
A própria função dos quadrados repete essencialmente o código da parte anterior, com a diferença de que o aumento do número de quadrados encontrados é feito usando atomicAdd - isso garante que a variável seja alterada corretamente durante chamadas simultâneas.
O resultado não requer comentários - o tempo de execução foi de
2,7 s , o que é cerca de 30 vezes melhor que a versão inicial de thread único:

Conforme sugerido nos comentários, você pode usar ainda mais blocos de hardware da placa de vídeo, portanto, a opção de 256 blocos foi tentada. Alterar o código é mínimo:
__global__ void squares(int *res_array) { int index1 = blockIdx.x/MAX, index2 = blockIdx.x%MAX; ... } squares<<<MAX*MAX, 1>>>(gpu_out);
Isso reduziu o tempo em mais 2 vezes, para
1,2s . Além disso, em cada bloco, 16 processos podem ser iniciados, o que dá o melhor tempo de
0,44s .
Código final #include <stdio.h> #include <ctime> #define N 4 #define MAX (N*N) #define SQ_MAX 8*1024 #define BLOCK_SIZE (SQ_MAX*N*N + 1) #define S 34 // Magic square: // x11 x12 x13 x14 // x21 x22 x23 x24 // x31 x32 x33 x34 // x41 x42 x43 x44 __global__ void squares(int *res_array) { int index1 = blockIdx.x/MAX, index2 = blockIdx.x%MAX, index3 = threadIdx.x; if (index1 + 1 > MAX || index2 + 1 > MAX || index3 + 1 > MAX) return; const int x11 = index1+1, x12 = index2+1, x13 = index3+1; if (x13 == x11 || x13 == x12) return; int x14 = S - x11 - x12 - x13; if (x14 < 1 || x14 > MAX) return; if (x14 == x11 || x14 == x12 || x14 == x13) return; for(int x21=1; x21<=MAX; x21++) { if (x21 == x11 || x21 == x12 || x21 == x13 || x21 == x14) continue; for(int x22=1; x22<=MAX; x22++) { if (x22 == x11 || x22 == x12 || x22 == x13 || x22 == x14 || x22 == x21) continue; for(int x23=1; x23<=MAX; x23++) { int x24 = S - x21 - x22 - x23; if (x24 < 1 || x24 > MAX) continue; if (x23 == x11 || x23 == x12 || x23 == x13 || x23 == x14 || x23 == x21 || x23 == x22) continue; if (x24 == x11 || x24 == x12 || x24 == x13 || x24 == x14 || x24 == x21 || x24 == x22 || x24 == x23) continue; for(int x31=1; x31<=MAX; x31++) { if (x31 == x11 || x31 == x12 || x31 == x13 || x31 == x14 || x31 == x21 || x31 == x22 || x31 == x23 || x31 == x24) continue; for(int x32=1; x32<=MAX; x32++) { if (x32 == x11 || x32 == x12 || x32 == x13 || x32 == x14 || x32 == x21 || x32 == x22 || x32 == x23 || x32 == x24 || x32 == x31) continue; for(int x33=1; x33<=MAX; x33++) { int x34 = S - x31 - x32 - x33; if (x34 < 1 || x34 > MAX) continue; if (x33 == x11 || x33 == x12 || x33 == x13 || x33 == x14 || x33 == x21 || x33 == x22 || x33 == x23 || x33 == x24 || x33 == x31 || x33 == x32) continue; if (x34 == x11 || x34 == x12 || x34 == x13 || x34 == x14 || x34 == x21 || x34 == x22 || x34 == x23 || x34 == x24 || x34 == x31 || x34 == x32 || x34 == x33) continue; const int x41 = S - x11 - x21 - x31, x42 = S - x12 - x22 - x32, x43 = S - x13 - x23 - x33, x44 = S - x14 - x24 - x34; if (x41 < 1 || x41 > MAX || x42 < 1 || x42 > MAX || x43 < 1 || x43 > MAX || x44 < 1 || x44 > MAX) continue; if (x41 == x11 || x41 == x12 || x41 == x13 || x41 == x14 || x41 == x21 || x41 == x22 || x41 == x23 || x41 == x24 || x41 == x31 || x41 == x32 || x41 == x33 || x41 == x34) continue; if (x42 == x11 || x42 == x12 || x42 == x13 || x42 == x14 || x42 == x21 || x42 == x22 || x42 == x23 || x42 == x24 || x42 == x31 || x42 == x32 || x42 == x33 || x42 == x34 || x42 == x41) continue; if (x43 == x11 || x43 == x12 || x43 == x13 || x43 == x14 || x43 == x21 || x43 == x22 || x43 == x23 || x43 == x24 || x43 == x31 || x43 == x32 || x43 == x33 || x43 == x34 || x43 == x41 || x43 == x42) continue; if (x44 == x11 || x44 == x12 || x44 == x13 || x44 == x14 || x44 == x21 || x44 == x22 || x44 == x23 || x44 == x24 || x44 == x31 || x44 == x32 || x44 == x33 || x44 == x34 || x44 == x41 || x44 == x42 || x44 == x43) continue; int sh1 = x11 + x12 + x13 + x14, sh2 = x21 + x22 + x23 + x24, sh3 = x31 + x32 + x33 + x34, sh4 = x41 + x42 + x43 + x44; int sv1 = x11 + x21 + x31 + x41, sv2 = x12 + x22 + x32 + x42, sv3 = x13 + x23 + x33 + x43, sv4 = x14 + x24 + x34 + x44; int sd1 = x11 + x22 + x33 + x44, sd2 = x14 + x23 + x32 + x41; if (sh1 != S || sh2 != S || sh3 != S || sh4 != S || sv1 != S || sv2 != S || sv3 != S || sv4 != S || sd1 != S || sd2 != S) continue; // Square found: save in array (MAX numbers for each square) int p = atomicAdd(res_array, 1); if (p >= SQ_MAX) continue; int i = MAX*p + 1; res_array[i] = x11; res_array[i+1] = x12; res_array[i+2] = x13; res_array[i+3] = x14; res_array[i+4] = x21; res_array[i+5] = x22; res_array[i+6] = x23; res_array[i+7] = x24; res_array[i+8] = x31; res_array[i+9] = x32; res_array[i+10] = x33; res_array[i+11] = x34; res_array[i+12]= x41; res_array[i+13]= x42; res_array[i+14] = x43; res_array[i+15] = x44; // Warning: printf from kernel makes calculation 2-3x slower // printf("%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d\n", x11, x12, x13, x14, x21, x22, x23, x24, x31, x32, x33, x34, x41, x42, x43, x44); } } } } } } } int main(int argc,char *argv[]) { int *gpu_out = NULL; cudaMalloc(&gpu_out, BLOCK_SIZE*sizeof(int)); const clock_t begin_time = clock(); int *results = (int*)malloc(BLOCK_SIZE*sizeof(int)); results[0] = 0; cudaMemcpy(gpu_out, results, BLOCK_SIZE*sizeof(int), cudaMemcpyHostToDevice); squares<<<MAX*MAX, MAX>>>(gpu_out); cudaMemcpy(results, gpu_out, BLOCK_SIZE*sizeof(int), cudaMemcpyDeviceToHost); // Print results int squares = results[0]; for(int p=0; p<SQ_MAX && p<squares; p++) { int i = MAX*p + 1; printf("[%d %d %d %d %d %d %d %d %d %d %d %d %d %d %d %d]\n", results[i], results[i+1], results[i+2], results[i+3], results[i+4], results[i+5], results[i+6], results[i+7], results[i+8], results[i+9], results[i+10], results[i+11], results[i+12], results[i+13], results[i+14], results[i+15]); } printf ("CNT: %d\n", squares); float diff_t = float(clock() - begin_time)/CLOCKS_PER_SEC; printf("T = %.2fs\n", diff_t); cudaFree(gpu_out); free(results); return 0; }
Provavelmente, isso está longe do ideal, por exemplo, você pode executar ainda mais blocos na GPU, mas isso tornará o código mais confuso e difícil de entender. E, é claro, os cálculos não são "gratuitos" - quando a GPU é carregada, a interface do Windows começa a diminuir visivelmente e o consumo de energia do computador aumenta quase duas vezes, de 65 para 130W.
Editar : como o usuário do
Bodigrim solicitou nos comentários, outra igualdade se aplica ao quadrado 4x4: a soma de 4 células "internas" é igual à soma das células "externas", também é S.

X22 + X23 + X32 + X33 = X11 + X41 + X14 + X44 = SIsso tornará possível acelerar o algoritmo, expressando algumas variáveis através de outras e removendo outros 1-2 loops aninhados; uma versão atualizada do código pode ser encontrada no comentário abaixo.Conclusão
A tarefa de encontrar “quadrados mágicos” acabou sendo tecnicamente muito interessante e, ao mesmo tempo, difícil. Mesmo com os cálculos na GPU, a busca por todos os quadrados 5x5 pode levar várias horas, e a otimização para encontrar quadrados mágicos de dimensões 7x7 e superiores ainda precisa ser feita.Matematicamente e algoritmicamente, também existem vários problemas não resolvidos:- « » N. 22 , 33 8 ( 1, ), 44 , 7040, . .
- , .
- . , NVIDIA Tesla , - , . , . , ;)
Um artigo separado pode ser escrito sobre a análise e as propriedades dos próprios quadrados mágicos, se houver interesse.PS: Para a pergunta que provavelmente se segue, "por que isso é necessário"? Em termos de consumo de energia, calcular quadrados mágicos não é melhor nem pior do que calcular bitcoins; então, por que não? Além disso, é um exercício interessante para a mente e uma tarefa interessante no campo da programação aplicada.