Curso MIT "Segurança de sistemas de computadores". Aula 10: Execução Simbólica, Parte 3

Instituto de Tecnologia de Massachusetts. Curso de Aula nº 6.858. "Segurança de sistemas de computador". Nikolai Zeldovich, James Mickens. 2014 ano

Computer Systems Security é um curso sobre o desenvolvimento e implementação de sistemas de computador seguros. As palestras abrangem modelos de ameaças, ataques que comprometem a segurança e técnicas de segurança baseadas em trabalhos científicos recentes. Os tópicos incluem segurança do sistema operacional (SO), recursos, gerenciamento de fluxo de informações, segurança de idiomas, protocolos de rede, segurança de hardware e segurança de aplicativos da web.

Palestra 1: “Introdução: modelos de ameaças” Parte 1 / Parte 2 / Parte 3
Palestra 2: “Controle de ataques de hackers” Parte 1 / Parte 2 / Parte 3
Aula 3: “Estouros de Buffer: Explorações e Proteção” Parte 1 / Parte 2 / Parte 3
Palestra 4: “Separação de Privilégios” Parte 1 / Parte 2 / Parte 3
Palestra 5: “De onde vêm os sistemas de segurança?” Parte 1 / Parte 2
Palestra 6: “Oportunidades” Parte 1 / Parte 2 / Parte 3
Palestra 7: “Sandbox do Cliente Nativo” Parte 1 / Parte 2 / Parte 3
Aula 8: “Modelo de Segurança de Rede” Parte 1 / Parte 2 / Parte 3
Aula 9: “Segurança de aplicativos da Web” Parte 1 / Parte 2 / Parte 3
Palestra 10: “Execução Simbólica” Parte 1 / Parte 2 / Parte 3

Agora, seguindo o ramo abaixo, vemos a expressão t = y. Como estamos considerando um caminho de cada vez, não precisamos introduzir uma nova variável para t. Podemos simplesmente dizer que, como t = y, t não é mais 0.

Continuamos descendo e chegamos ao ponto em que chegamos a outro ramo. Qual é a nova suposição que devemos fazer para seguir mais adiante neste caminho? Essa é uma suposição de que t <y.

O que é t? Se você procurar o ramo certo, veremos que t = y. E em nossa tabela, T = ye Y = y. Segue-se logicamente que nossa restrição se parece com y <y, o que não pode ser.



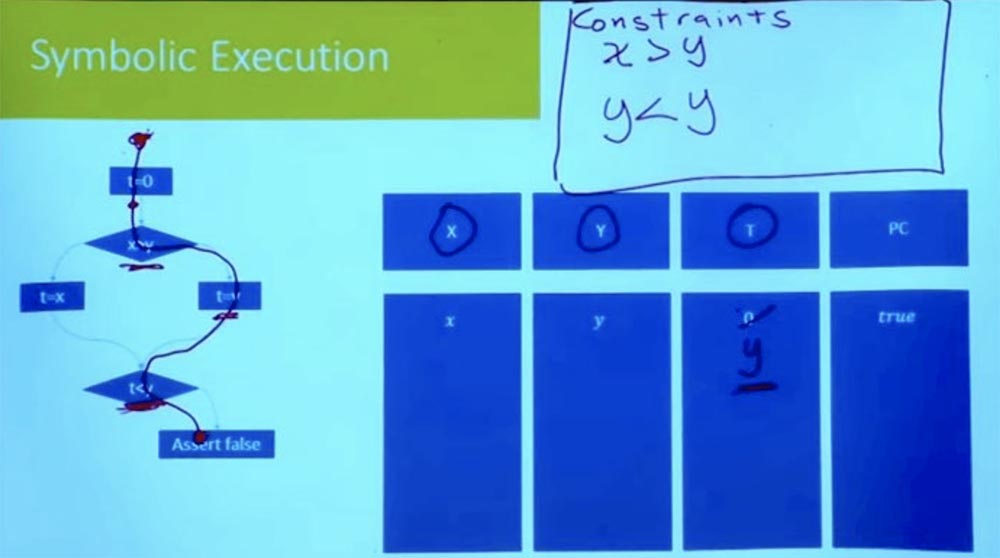
Assim, tínhamos tudo em ordem até chegarmos a esse ponto t <y. Até chegarmos à afirmação falsa, temos todas as desigualdades para estar corretas. Mas isso não funciona, porque ao executar tarefas do ramo certo, temos uma inconsistência lógica.

Temos o que costuma ser chamado de condição do caminho. Essa condição deve ser verdadeira para o programa seguir esse caminho. Mas sabemos que essa condição não pode ser atendida, portanto, é impossível que o programa siga esse caminho. Portanto, esse caminho já foi completamente eliminado e sabemos que esse caminho certo não pode ser percorrido.

E o outro lado? Vamos tentar percorrer o ramo esquerdo de uma maneira diferente. Quais serão as condições para esse caminho? Novamente, nosso estado simbólico começa em t = 0, e X e Y são iguais às variáveis ​​x e y.



Como é a restrição de caminho neste caso agora? Denotamos o ramo esquerdo como True e o ramo direito como False e consideramos ainda o valor t = x. Como resultado do processamento lógico das condições t = x, x> ye t <y, obtemos que simultaneamente temos o que x> y e x <y.



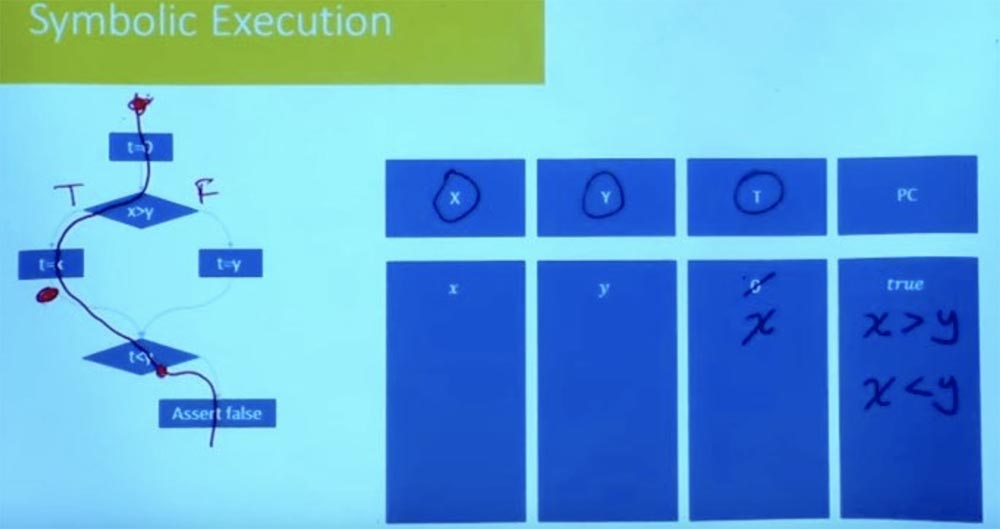
É claro que essa condição do caminho é insatisfatória. Não podemos ter x maior e menor que y. Não há atribuição para uma variável X que satisfaça as duas restrições. Assim, isso nos diz que o outro caminho também é insatisfatório.

Acontece que, neste momento, exploramos todos os caminhos possíveis no programa que podem nos levar a esse estado. Podemos realmente estabelecer e verificar se não há uma maneira possível de nos levar a uma afirmação falsa.
Público: neste exemplo, você mostrou que estudou o progresso de um programa em todas as ramificações possíveis. Mas uma das vantagens da execução simbólica é que não precisamos estudar todos os caminhos exponenciais possíveis. Então, como evitar isso neste exemplo?

Professor: Essa é uma pergunta muito boa. Nesse caso, você compromete entre a execução do personagem e o quão específico você quer ser. Portanto, neste caso, não estamos usando tanto a execução simbólica quanto a primeira vez que analisamos o fluxo do programa em ambos os ramos simultaneamente. Mas, graças a isso, nossas limitações se tornaram muito, muito simples.

As restrições individuais “uma maneira após a outra” são muito simples, mas você precisa fazer isso repetidamente, estudando todos os ramos existentes e exponencialmente - e todos os modos possíveis.
Existem muitos caminhos exponencialmente, mas para cada caminho como um todo, há também um conjunto exponencialmente grande de dados de entrada que podem seguir esse caminho. Portanto, isso já oferece uma grande vantagem, porque, em vez de tentar todas as entradas possíveis, você está tentando tentar de todas as maneiras possíveis. Mas você pode fazer algo melhor?

Essa é uma área em que muita experimentação foi feita com relação à execução simbólica, por exemplo, a execução simultânea de vários caminhos. Nos materiais das palestras, você encontrou heurísticas e um conjunto de estratégias que os pesquisadores usaram para tornar a pesquisa mais solucionável.

Por exemplo, uma das coisas que eles fazem é explorar um caminho após o outro, mas não o fazem completamente às cegas. Eles verificam as condições do caminho após cada etapa executada. Suponha que aqui em nosso programa, em vez de dizer "falso", houvesse uma árvore complexa de programas, um gráfico de fluxo de controle.



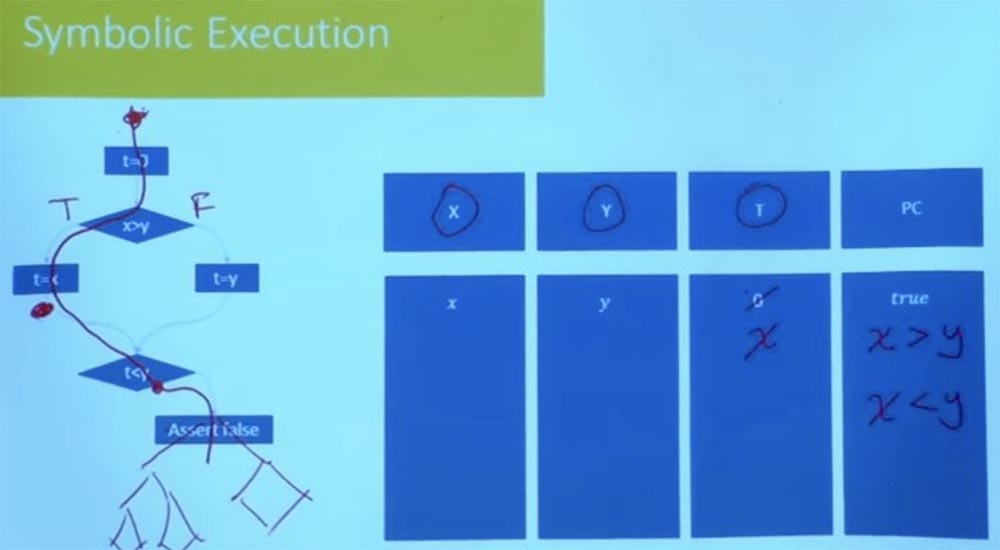
Você não precisa esperar até chegar ao final para verificar se esse caminho é viável. Nesse momento, quando você atinge a condição t <y, você já sabe que esse caminho é insatisfatório e nunca seguirá nessa direção. Portanto, cortar as ramificações incorretas no início do programa reduz a quantidade de trabalho empírico. A exploração razoável do caminho evita a possibilidade de falha no programa no futuro. Muitas das ferramentas práticas usadas hoje começam principalmente com testes aleatórios para obter o conjunto inicial de caminhos, após o qual eles começarão a explorar os caminhos na vizinhança. Eles processam muitas opções para a possível execução do programa para cada uma das filiais, imaginando o que acontece nesses caminhos.

É especialmente útil se tivermos um bom conjunto de testes. Você executa seu teste e descobre que esse pedaço de código não está sendo executado. Portanto, você pode seguir o caminho que mais se aproximou da implementação do código e perguntar se esse caminho pode ser alterado para seguir na direção certa.



Mas no momento em que você está tentando fazer todos os caminhos ao mesmo tempo, começam as restrições que se tornam intratáveis. Portanto, o que você pode fazer é executar uma função por vez, enquanto você pode aprender todos os caminhos de uma função juntos. Se você tentar fazer blocos grandes, em geral, poderá explorar todas as formas possíveis.

O mais importante é que, para cada filial, você verifique suas restrições e determine se essa ramificação pode realmente ser nos dois sentidos. Se ela não puder seguir os dois caminhos, você economiza tempo e esforço ao não seguir na direção em que ela não pode ir. Além disso, não me lembro das estratégias específicas usadas para encontrar maneiras com maior probabilidade de produzir resultados muito bons. Mas cortar os galhos errados no estágio inicial é muito importante.

Até agora, conversamos principalmente sobre "código de brinquedo", sobre variáveis ​​inteiras, sobre ramificações, sobre coisas muito simples. Mas o que acontece quando você tem um programa mais complexo? Em particular, o que acontece quando você tem um programa que inclui muitos?



Historicamente, o monte de hip tem sido a maldição de toda análise de software, porque as coisas limpas e elegantes do tempo de Fortran explodem completamente quando você tenta executá-las usando programas C nos quais você aloca memória esquerda e direita. Lá você tem sobreposições e toda a bagunça associada ao programa com memória alocada e ponteiros aritméticos. Essa é uma das áreas em que a execução simbólica tem uma excelente capacidade de raciocinar sobre programas.

Então, como fazemos isso? Vamos esquecer os galhos e controlar o fluxo por um momento. Temos um programa simples aqui. Aloca um pouco de memória, anula-o e obtém um novo ponteiro y do ponteiro x. Então ela escreve algo para y e verifica se o valor armazenado no ponteiro y é igual ao valor armazenado no ponteiro x?

Com base no conhecimento básico de C, você pode ver que essa verificação não é executada porque x é redefinido e y = 25; portanto, x indica um local diferente. Até agora, está tudo bem conosco.
A maneira como modelamos a pilha, e a maneira como a pilha é modelada na maioria dos sistemas, usa a representação da pilha em C, onde é apenas uma base de endereços gigantesca, uma matriz gigantesca na qual você pode colocar seus dados.
Isso significa que podemos representar nosso programa como um conjunto de dados global muito grande, que será chamado de MEM. Essa é uma matriz que essencialmente vai mapear endereços para valores. Um endereço é apenas um valor de 64 bits. E o que acontecerá depois que você ler algo deste endereço? Depende de como você modela a memória.

Se você modelá-lo no nível de bytes, você obtém um byte. Se você modelá-lo no nível da palavra, você obtém uma palavra. Dependendo do tipo de erro em que você está interessado e se você está preocupado com a alocação de memória ou não, você o modelará de maneira um pouco diferente, mas geralmente a memória é apenas uma matriz do endereço ao valor.



Portanto, o endereço é apenas um número inteiro. De certa forma, não importa o que C pense no endereço, é apenas um número inteiro de 64 ou 32 bits, dependendo da sua máquina. É simplesmente um valor indexado nessa memória. E o que você pode colocar na memória, pode ler a partir dessa memória.

Portanto, coisas como aritmética de ponteiro se tornam aritméticas inteiras. Na prática, existem algumas dificuldades, porque em C, a aritmética de ponteiros conhece os tipos de ponteiros e elas aumentam em proporção ao tamanho. Portanto, como resultado, obtemos a seguinte linha:

y = x + 10;  sizeof (int)



Mas o que realmente importa é o que acontece quando você escreve e lê de memória. Com base no ponteiro em que 25 deve ser escrito em y, pego uma matriz de memória e a indexo com y. E escrevo 25 para este local de memória.

Depois, passo para a instrução MEM [y] = MEM [x], leio o valor do local y na memória, leio o valor do local x na memória e os comparo entre si. Então eu verifico se eles correspondem ou não.

Essa é uma suposição muito simples, permitindo que você alterne de um programa que usa heap para um programa que usa essa matriz global gigantesca que representa memória. Isso significa que agora, ao falar sobre programas que gerenciam o heap, você realmente não precisa falar sobre programas que gerenciam o heap. Você conseguirá falar perfeitamente sobre matrizes, e não sobre montões.

Aqui está outra pergunta simples. E a função malloc? Você pode simplesmente usar e usar a implementação malloc em C, acompanhar todas as páginas destacadas, acompanhar tudo o que foi liberado, apenas ter uma lista gratuita e isso é o suficiente. Acontece que, para muitos propósitos e para muitos tipos de erros, você não precisa do malloc para ser complexo.

De fato, você pode alternar do malloc, que se parece com isto: x = malloc (sizeof (int) * 100), para malloc desse tipo:

POS = 1
Int malloc (int n) {
rv = POS
POS + = n;
}

O que simplesmente diz: "Vou guardar o contador para o próximo espaço livre na memória e, sempre que alguém pedir um endereço, dou a ele esse local e aumento essa posição e depois retorno rv". Nesse caso, qual malloc no sentido tradicional é completamente ignorado.



Nesse caso, não há liberação de memória. A função simplesmente continua a se mover cada vez mais longe da memória, e mais e mais, e é aí que termina sem qualquer liberação. Ela também não se importa com o fato de haver áreas de memória nas quais não vale a pena escrever, porque existem endereços especiais de importância especial reservados ao sistema operacional.

Ele não modela nada que torne a escrita da função malloc complicada, mas apenas em um certo nível de abstração, quando você tenta falar sobre algum tipo de código complexo que executa manipulações de ponteiro.

Ao mesmo tempo, você não se preocupa em liberar memória, mas está preocupado se o programa irá, por exemplo, gravar fora de um buffer, caso em que essa função malloc pode ser bastante boa.



E isso realmente acontece com muita frequência quando você executa a execução simbólica do código real. Uma etapa muito importante é modelar as funções da sua biblioteca. A maneira como você modela as funções da biblioteca terá um enorme impacto, por um lado, no desempenho e na escalabilidade da análise, mas, por outro lado, também afetará a precisão.

Portanto, se você tiver um malloc de modelo "brinquedo", como este, ele agirá muito rapidamente, mas ao mesmo tempo haverá certos tipos de erros que você não poderá perceber. Assim, por exemplo, neste modelo eu ignoro completamente as distribuições, para que eu possa receber um erro se alguém obtiver acesso ao espaço não alocado. Portanto, na vida real, nunca vou usar esse modelo malloc de Mickey Mouse.

Portanto, é sempre um equilíbrio entre precisão da análise e eficiência. E quanto mais complexos forem os modelos de funções padrão, como malloc, menos escalável será sua análise. Mas, para algumas classes de erro, você precisará desses modelos simples. Portanto, várias bibliotecas em C são de grande importância, necessárias para entender o que esse programa realmente faz.

Portanto, reduzimos o problema de raciocinar sobre o heap ao raciocinar sobre o programa com matrizes, mas eu realmente não disse como raciocinar sobre o programa com matrizes. Acontece que a maioria dos solucionadores SMT suporta a teoria de arrays.



A idéia é que, se a é uma matriz, existe alguma notação que permite que você pegue essa matriz e crie uma nova matriz, onde o local i é atualizado para o valor e. Isso está claro?

Portanto, se eu tiver uma matriz a e fizer essa operação de atualização e tentar ler o valor de k, isso significa que o valor de k será igual ao valor de k na matriz a, se k for diferente de i e será igual a e, se k é igual a i.

Atualizar uma matriz significa que você precisa pegar a matriz antiga e atualizá-la com uma nova matriz. Bem, se você tem uma fórmula que inclui a teoria das matrizes, é por isso que comecei com uma matriz zero, que em todos os lugares é representada simplesmente por zeros.



Em seguida, escrevo 5 no local ie 7 no local j, após o qual leio de ke verifico se é 5 ou não. Em seguida, ele pode ser expandido usando a definição de algo que diz, por exemplo: “se k é iek é y, enquanto k é diferente de j, então sim, será 5, caso contrário, não será. 5 ".

E, na prática, os solucionadores SMT não apenas expandem isso para muitas fórmulas booleanas, eles usam essa estratégia de vaivém entre o solucionador SAT e o mecanismo, que é capaz de falar sobre a teoria de arrays para realizar este trabalho.

O importante é que, contando com essa teoria de matrizes, usando a mesma estratégia que aplicamos para gerar fórmulas para números inteiros, você pode realmente gerar fórmulas que incluem lógica de matriz, atualizações de matriz, eixos de matriz, iteração de matriz. E desde que você corrija seu caminho, essas fórmulas são muito fáceis de gerar.
Se você não corrigir seus caminhos, mas quiser criar uma fórmula que corresponda à passagem do programa em todos os caminhos, isso também será relativamente fácil. A única coisa com a qual você precisa lidar é com um tipo especial de loops.

Dicionários e mapas também são muito fáceis de modelar usando funções indefinidas. Na verdade, a própria teoria das matrizes é apenas um caso especial de uma função indefinida. Com a ajuda de tais funções, coisas mais complicadas podem ser feitas. No solucionador SMT moderno, há suporte interno para raciocinar sobre conjuntos e operações de conjunto, o que pode ser muito útil se você estiver falando de um programa que inclui conjuntos de cálculo.

Ao projetar uma dessas ferramentas, a fase de modelagem é muito importante. E o ponto não é apenas como você modela funções complexas de programas de acordo com suas teorias, por exemplo, coisas como reduzir montes a matrizes. A questão também é quais teorias e solucionadores você usa. Há um grande número de teorias e solucionadores com diferentes relacionamentos, para os quais é necessário escolher um compromisso razoável entre eficiência e custo.



A maioria das ferramentas práticas adere à teoria dos vetores de bits e, se necessário, pode usar a teoria das matrizes para modelar pilhas. Em geral, ferramentas práticas tentam evitar teorias mais complexas, como a teoria dos conjuntos. Isso ocorre porque eles geralmente são menos escaláveis ​​em alguns casos, se você não estiver lidando com um programa que realmente exija ferramentas desse tipo para funcionar.

Público: além do estudo do desempenho simbólico, em que os desenvolvedores se concentram?

: — , . , , , , . , .

, , . , , , , , , , .

, — , , . , , — , JavaScript Python, . , .



, Python. , , : «, , , ». .

, , , , , .
, , , - , , .

, , , . , , Microsoft Word, , , .

, , , , .

, . , , - , - . , , . , .


A versão completa do curso está disponível aqui .

, . ? ? , 30% entry-level , : VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps $20 ? ( RAID1 RAID10, 24 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD de 1Gbps até dezembro de graça quando pagar por um período de seis meses, você pode fazer o pedido aqui .

Dell R730xd 2 ? 2 Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 $249 ! . c Dell R730xd 5-2650 v4 9000 ?