Curso MIT "Segurança de sistemas de computadores". Palestra 10: Execução Simbólica, Parte 2

Instituto de Tecnologia de Massachusetts. Curso de Aula nº 6.858. "Segurança de sistemas de computador". Nikolai Zeldovich, James Mickens. 2014 ano

Computer Systems Security é um curso sobre o desenvolvimento e implementação de sistemas de computador seguros. As palestras abrangem modelos de ameaças, ataques que comprometem a segurança e técnicas de segurança baseadas em trabalhos científicos recentes. Os tópicos incluem segurança do sistema operacional (SO), recursos, gerenciamento de fluxo de informações, segurança de idiomas, protocolos de rede, segurança de hardware e segurança de aplicativos da web.

Palestra 1: “Introdução: modelos de ameaças” Parte 1 / Parte 2 / Parte 3
Palestra 2: “Controle de ataques de hackers” Parte 1 / Parte 2 / Parte 3
Aula 3: “Estouros de Buffer: Explorações e Proteção” Parte 1 / Parte 2 / Parte 3
Palestra 4: “Separação de Privilégios” Parte 1 / Parte 2 / Parte 3
Palestra 5: “De onde vêm os sistemas de segurança?” Parte 1 / Parte 2
Palestra 6: “Oportunidades” Parte 1 / Parte 2 / Parte 3
Palestra 7: “Sandbox do Cliente Nativo” Parte 1 / Parte 2 / Parte 3
Aula 8: “Modelo de Segurança de Rede” Parte 1 / Parte 2 / Parte 3
Aula 9: “Segurança de aplicativos da Web” Parte 1 / Parte 2 / Parte 3
Palestra 10: “Execução Simbólica” Parte 1 / Parte 2 / Parte 3

Público: Parece que você não falou sobre como os bits são usados ​​para armazenar um número inteiro int.

Professor: Essa é uma pergunta muito boa. E realmente tem a ver com a forma como você define suas limitações, certo? Portanto, se você olhar para o nosso exemplo simples desde o início, verá que assumimos a presença de números inteiros que estudamos no ensino fundamental. Ao mesmo tempo, decidimos ignorar completamente os erros de estouro. Se você se preocupa com erros de estouro, e é importante que você não exista esses erros, o uso de números inteiros matematicamente não ajudará a corrigir o problema.



O que você precisa é apresentar essas quantidades não como números inteiros, mas como vetores de bits. Ao representá-los como vetores de bits, você deve usar uma visão mais ampla das coisas. Aqui voltamos aos solucionadores SMT. Um aspecto da teoria modular é que o solucionador em si é extensível usando diferentes teorias.

As teorias mais populares são as de vetores de bits de comprimento fixo. Isso significa que, se você interpreta suas fórmulas na teoria dos vetores de bits de comprimento fixo, deve primeiro definir o comprimento dos vetores de bits. Ou seja, você deve indicar explicitamente que isso será usado para vetores de bits com 32 bits ou 8 bits ou 64 bits.



Há uma outra teoria chamada teoria da matriz TOA. E falaremos um pouco mais sobre isso. Diferentemente da teoria dos vetores de bits, projetada para objetos de comprimento fixo, a teoria das matrizes é destinada a coleções cujo tamanho é a priori desconhecido.

Agora, na prática, ninguém usa a teoria das matrizes, por exemplo, para modelar números inteiros, porque é muito caro. Falar sobre um problema é muito mais caro quando você não conhece seus limites. Portanto, como regra, as pessoas usam a teoria de um comprimento fixo de vetores de bits nas discussões de números inteiros ou mesmo símbolos.

Outra teoria muito difundida é a teoria da aritmética de número inteiro real e, em particular, a aritmética de número inteiro linear.



As pessoas gostam muito dessa teoria porque ela fornece argumentação eficaz, mas não é muito boa quando você fala sobre programas, porque aqui você realmente se importa com problemas de transbordamento. Mas essa teoria é amplamente usada para muitas coisas.

Outra teoria que é freqüentemente usada é a teoria das funções não interpretadas. O que essa teoria significa?



Isso significa que você tem uma certa fórmula. Nesta fórmula, você sabe que está chamando uma função, mas não sabe nada sobre essa função, exceto pelo fato de que se você inserir alguma entrada nela, obterá a mesma saída.

Acontece que isso é muito útil ao raciocinar sobre coisas como o uso de código de ponto flutuante, modelagem, senos, cossenos, raízes quadradas. Discussões detalhadas sobre essas coisas podem ser muito demoradas e caras. Mas usar essa teoria permite que você diga: "Olha, eu realmente não me importo com o que a função senoidal faz. Eu não ligo para o que exatamente ela vai dar. Eu só preciso saber que se eu chamar a função seno em vários locais do programa com entrada específica, obterá dados do mesmo tipo na saída. Isso é o suficiente para eu raciocinar sobre o meu programa. ”

E, portanto, as operações mais comuns na análise de sistemas reais são vetores de bits que funcionam com números inteiros, logs e ponteiros. De fato, os ponteiros geralmente são representados por um número inteiro, porque às vezes você não define vetores de bits nos ponteiros. Mas, às vezes, você precisa fazer isso e não pode mais usar números inteiros.

Então, examinamos o que um solucionador SMT pode fazer por você. Como isso realmente funciona? O que há dentro deles que os faz funcionar?

De fato, os solucionadores SMT dependem de nossa capacidade de resolver os problemas de viabilidade das fórmulas booleanas SAT, de considerar problemas associados apenas a restrições puramente booleanas e variáveis ​​booleanas e nos informar se você garantirá que o programa atribua os valores atribuídos a essas variáveis ​​booleanas ou não. .

Isso é algo que por muitos e muitos anos ensinou aos alunos mais velhos, dizendo que essa é realmente uma tarefa completa do NP e, nos casos em que algo se resume ao SAT, você não deve fazer isso. Mas, na verdade, temos realmente bons solucionadores de SAT.

Então, vou lhe contar a idéia básica de como os solucionadores de SAT funcionam. Está no fato de você pegar todas as suas restrições nas variáveis ​​booleanas e colocá-las no banco de dados. Talvez você não consiga ver claramente as letras minúsculas na tela, mas é tudo o que posso fazer.



Vou comentar e falar sobre isso no decorrer da ação, e depois publicarei os slides para que você possa ver o que está escrito lá.

Então, aqui na tarefa SAT, temos todas essas variáveis ​​representando incógnitas booleanas, certo? Queremos saber se é possível que X seja verdadeiro ao mesmo tempo (X = VERDADEIRO), e Y seja verdadeiro e Z seja verdadeiro. Estas são as nossas incógnitas. Além disso, todas as restrições estão na forma conjuntiva normal. Isso significa que todas as nossas restrições estão na forma de X1 = verdadeiro, ou X2 = verdadeiro ou X3 = verdadeiro.



Nesta forma, temos todas as nossas limitações, que dizem que X1 é verdadeiro ou X2 é falso ou X3 é falso. Você provavelmente lembra da matemática discreta que qualquer fórmula booleana pode ser representada na forma conectiva normal. Isso significa que, qualquer representação usada para representar fórmulas booleanas, você pode facilmente converter para esse formato.

Portanto, temos um banco de dados com muitas limitações deste formulário. O solucionador SAT escolherá uma dessas variáveis ​​aleatoriamente, suponha que seja X1. E ele dirá: “por que não definir X1 como verdadeiro? Eu não sei nada sobre essas restrições, então posso assumir que é isso mesmo. " E acontece que você terá restrições que, por exemplo, afirmam que X1 é falso ou X7 é verdadeiro.

Portanto, se você sabe que X1 é verdadeiro e sabe que X1 é falso ou X7 é verdadeiro, o que você sabe sobre X7?

Público: deve ser verdade!

Professor: sim, deve ser verdade. Porque, caso contrário, esta restrição não será cumprida. Portanto, agora você distribuiu esse valor de X1 para X7. Suponha que você agora selecione outra variável aleatória, como X5.



Agora, suponha que você tenha uma restrição que diz: X7 é falso ou X6 é verdadeiro ou X5 é falso. Então, eu tenho X5 = verdadeiro e X7 = verdadeiro. Isso significa que o X6 agora também deve ser verdadeiro. Porque, caso contrário, essa restrição seria violada. Portanto, o sistema conclui que o X6 deve ser verdadeiro e continua o processo, executando as verificações disponíveis e analisando todas as ofertas disponíveis. O sistema verifica se há outras coisas implícitas nas verificações que possui. E ela segue esses significados até que uma de duas coisas aconteça.

A primeira é que você segue as consequências e tenta coisas aleatórias e, por fim, define o valor de cada variável sem nunca encontrar uma contradição. Então você fez tudo certo.

A segunda - você se depara com uma contradição e volta à condição que fez X4 ser verdadeiro, excluindo a condição que fez X4 ser falso. Mas há uma regra da álgebra booleana que todos deveriam conhecer: uma variável não pode ser verdadeira e falsa ao mesmo tempo.



E diz que você se depara com uma contradição, obviamente fez algo errado em uma dessas tarefas aleatórias que tentou concluir.

Vamos analisar essa contradição e ver que tipo de tarefas levaram a essa contradição. Com base nas atribuições que levaram a essa contradição, vamos apresentar uma nova cláusula de conflito que resume essa contradição.

O que acontece que X1 é falso e X5 é falso e X9 também é falso? Basicamente, isso se baseia no que aprendi com essas tarefas aleatórias, durante as quais descobri que uma dessas coisas deve ser verdadeira, que não é possível que X1 seja verdadeiro e X5 seja verdadeiro, e X9 seja false, isso não pode ser.

Sei que isso não pode acontecer, porque quando tentei fazer tudo "explodir", encerrei o programa com uma contradição.

E assim, o solucionador SAT tenta concluir tarefas aleatórias, verificando como elas são. Quando ele encontra contradições, ele analisa o conjunto de consequências que as levaram e, finalmente, forma uma nova restrição, que garante que o solucionador nunca mais encontre essa contradição específica, esse problema específico.
Assim, podemos imaginar o solucionador SAT como uma "caixa preta" que fornece uma restrição booleana e pode dizer se é satisfatório ou não. Os solucionadores SMT são construídos sobre os melhores solucionadores SAT. Eles podem usar o poder dos solucionadores de SAT para resolver problemas completos de NP com raciocínio orientado ao assunto sobre teorias suportadas.

Para ter uma idéia de como isso funciona, suponha que você tenha essa fórmula.



Isso é factível? Podemos encontrar um teste satisfatório para ela? O solucionador SMT pode separar parte dessa fórmula, o que requer raciocínio na teoria dos números inteiros. Usamos estruturas booleanas para separar fórmulas. Portanto, temos as fórmulas F1, F2, F3 e F4.



Agora, essa é uma tarefa booleana puramente lógica - posso encontrar uma tarefa satisfatória para isso? O solucionador do SAT pode dizer: "sim, posso encontrar algo que satisfaça essa tarefa executando F1 = true, F2 = true e F3 = true". Isso satisfaz a especificação da fórmula booleana.

\

Então, agora temos uma pergunta que podemos pedir ao solucionador para uma área específica, neste caso, é apenas um solucionador aritmético linear. Assim, podemos ir ao solucionador linear do solucionador de teoria e dizer: "O solucionador de SAT afirma que essa é uma tarefa razoável e que, se eu puder fazer essa tarefa funcionar, minha fórmula será satisfeita".

Posso dizer que F1 é X> 5, F2 é Y <5 e F3 é Y> X. Então, posso perguntar ao solucionador SAT se é possível obter esses X e Y para que X seja> 5, Y é < 5 e, nesse caso, Y seria> X? Agora, esta é uma questão de aritmética puramente linear, não há lógica booleana.

E qual é a resposta para esta pergunta? Não. É impossível satisfazer essas condições ao mesmo tempo.
Portanto, existem métodos tradicionais para resolver problemas lineares. Você pode usar o método simplex, por exemplo, para resolver sistemas de desigualdades lineares. Existem muitos métodos que podem ser usados ​​para resolver sistemas de desigualdades lineares.



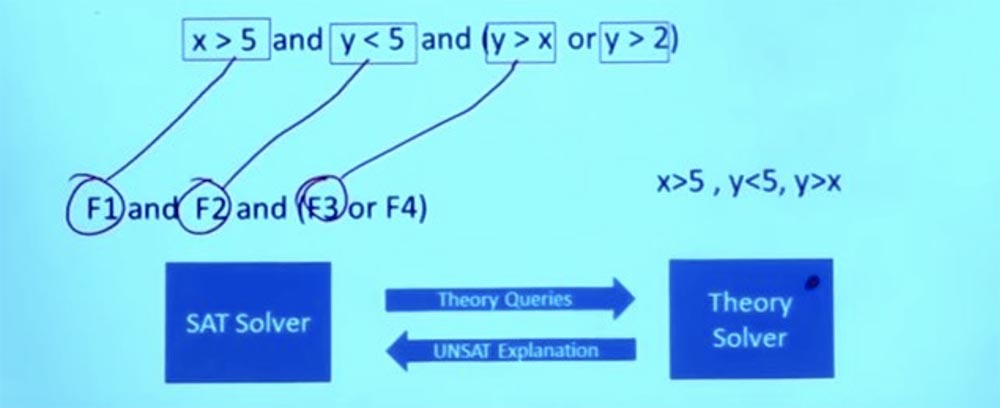
Assim, o solucionador SAT envia perguntas teóricas ao solucionador de Teoria. O ponto principal é que os solucionadores de solucionadores de teoria sabem tudo sobre esses problemas e podem dar uma resposta precisa à questão de saber se essas condições funcionarão.

Nesse caso, o solucionador teórico processa a solicitação, descobre que essa atribuição de condições não pode funcionar, retorna ao solucionador SAT e diz: “o que você fez não funcionará”!

Mas ele não apenas diz sim ou não, mas explica por que algo não vai funcionar. Pelo fato de essas fórmulas não funcionarem, o solucionador de teoria conclui que F1 e F2 e F3 não podem existir simultaneamente e informa ao solucionador de SAT que essas 3 fórmulas são mutuamente exclusivas.

Portanto, agora temos algumas das informações que posso retornar ao solucionador do SAT e perguntamos a ele: “ei, você pode me dar uma solução que satisfaça não apenas a restrição que tínhamos no início, mas também a nova restrição que a Theory descobriu. solucionador "?

Existe algum outro objetivo que agora satisfaça essas duas limitações?



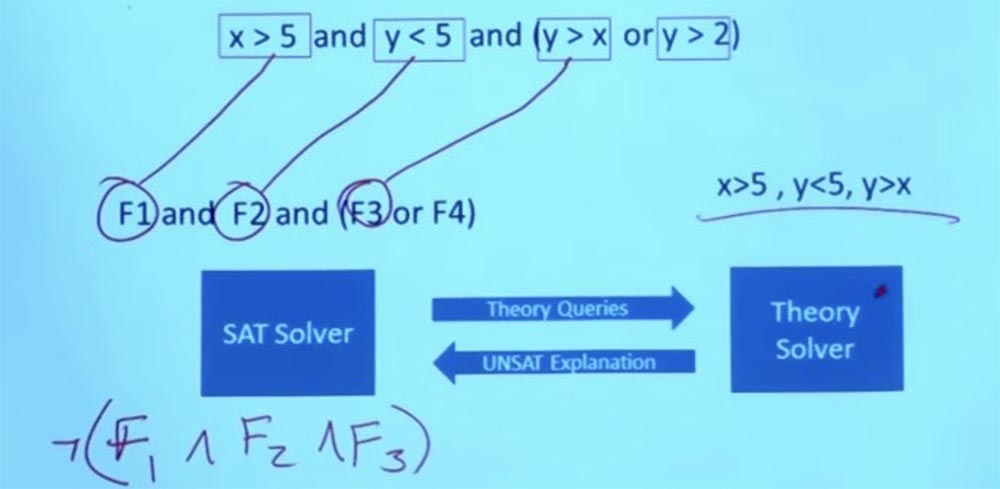
Então, descartamos a restrição inicial X> 5, Y <5, Y> X, isso não nos incomoda mais.



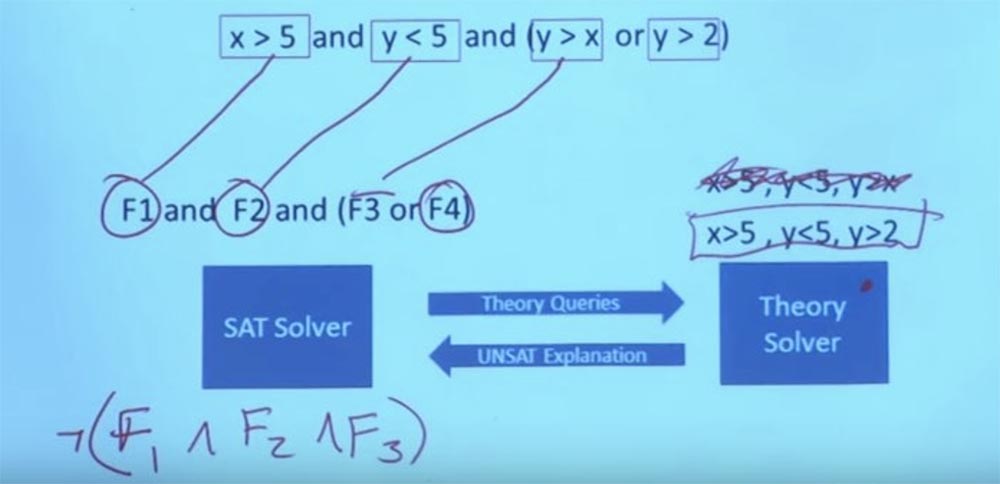
Temos uma nova restrição que podemos definir para nosso solucionador de Teoria - X> 5, Y <5, Y> 2. Podemos fazer Y igual a 3 e X igual a 6, e então ele funcionará. Agora você tem uma tarefa que satisfaz a fórmula na teoria e satisfaz a estrutura booleana desse objetivo. E com isso, o sistema pode voltar e dizer: "Sim, esta é a tarefa que satisfaz todas as suas limitações". Essa é a interação entre o solucionador de teoria e o solucionador de SAT. Na realidade, isso significa poder falar sobre fórmulas booleanas muito, muito grandes e muito complexas. Aqui está o que torna possível a execução simbólica.

Agora consideraremos a próxima pergunta - como é realizada a transição do programa para as restrições que podemos fornecer ao solucionador SMT.

Público: está construindo um SMT solver NP-complete ou não?

Professor: O solucionador SMT é essencialmente um problema canônico de NP-completo. Mas a maioria dos solucionadores atualmente inclui suporte para certas teorias que são completamente insolúveis.

Público: como você aborda esse problema no seu sistema?

Professor: bem, no final, você receberá uma restrição criada a partir deste programa. Você vai entregá-lo ao solucionador SMT. E o fato de serem tarefas NP completas ou de serem insatisfatórias significa que, se você tiver sorte, receberá uma resposta em questão de segundos. Mas se você não tiver sorte, pode levar mais tempo do que a criação do universo levou.



Público: acontece que as tarefas do sistema linear não passam no SAT?

Professor: sim, isso realmente acontece. No entanto, as ferramentas de engenharia existentes o tornam menos comum. Não resolvemos problemas aleatórios de SAT, não resolvemos problemas completamente aleatórios de vetores de bits.

Resolvemos problemas que possuem uma certa estrutura para que uma pessoa possa observá-la e ter alguma confiança de que ela funcionará. Estamos tentando criar alguns argumentos em sua cabeça para entender por que isso funcionou. E os solucionadores SAT usam essa estrutura. Seu problema pode ter um milhão de variáveis ​​booleanas, mas, na realidade, a maioria dessas variáveis ​​depende muito dos valores uma da outra. Assim, o número de graus de liberdade no problema é realmente muito menor do que o que milhões de variáveis ​​sugerem.

Público: você diz que não se trata de uma pergunta do exame, mas da vida real. Uma vez que alguém tenha construído esse sistema, ele deve funcionar e fazer sentido. Portanto, esse provavelmente não será um dos discursos teóricos desnecessários.

Professor: é isso. Portanto, na prática, quando você usa essa ferramenta, o que você sempre faz é definir tempos limite. Em geral, tudo acontece porque a exponencialidade não significa que você não pode fazer isso. Exponencialidade, isto é, quando uma função é limitada por outra, significa simplesmente que existe uma parede de tijolos à frente da qual essas coisas funcionarão, e elas funcionarão muito rapidamente. A exponencialidade funciona em ambas as direções.



Quando você se afasta dessa parede, as coisas crescem muito rapidamente, mas quando você aborda problemas menores ou mais simples, esses problemas também aceleram muito, muito rapidamente. Isso significa que muitos problemas terminam muito rapidamente. E então ocorre o tempo limite do problema. O objetivo é projetar coisas para que entre os problemas que terminam rapidamente estejam os que trazem benefícios práticos. Esses são os problemas que apontam para as vulnerabilidades de segurança do seu sistema, para erros, para caminhos que você talvez não tenha explorado antes ou para entradas que violem seus caminhos se você não as investigar previamente.

Então, sabemos como passar de uma fórmula, de um conjunto de restrições para uma resposta que diz: "Sim, essa fórmula tem uma solução, e aqui está, essa é uma solução". Ou ele dirá: "essa fórmula é insatisfatória, porque não há dados que satisfaçam suas tarefas". Então, como obtemos a fórmula do programa?

Ao executar a execução simbólica, você vai para o ramo e não sabe em qual direção ele irá. Existem duas opções para o que fazer neste caso. — , , , .

, , . , SMT-. . , .

: « , , , , ».

, , . . , .

, . , , . , – , . ? , .



, , t=0 false.



, , ? : , , .

, , , , , , .

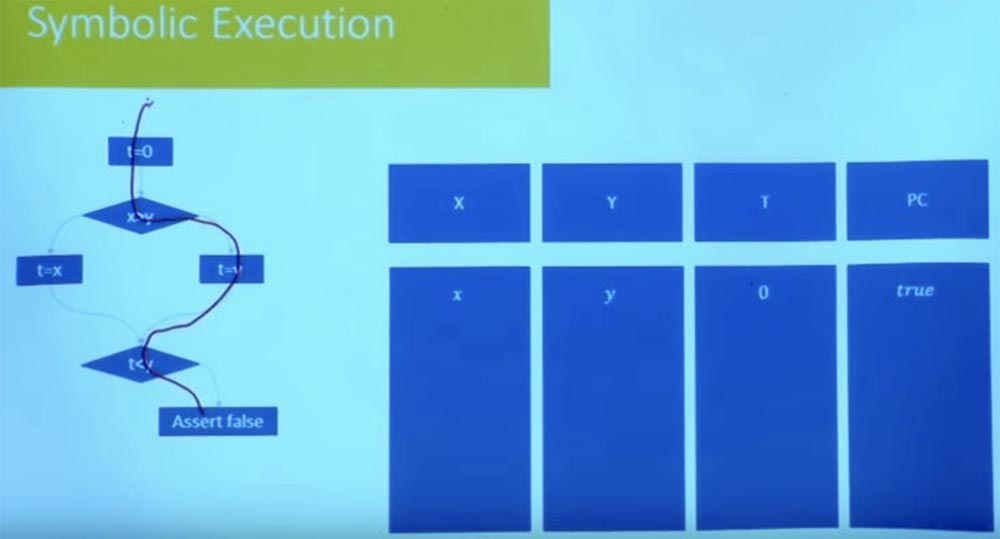
, , t = 0, x, y 0. , . , , X , Y.

, X > Y.



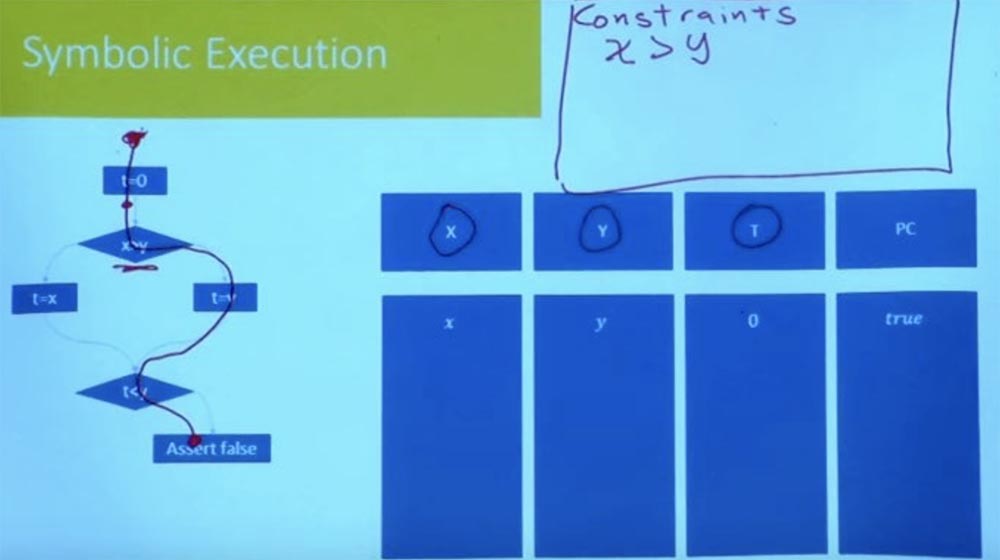
55:00

MIT « ». 10: « », 3


A versão completa do curso está disponível aqui .

, . ? ? , 30% entry-level , : VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps $20 ? ( RAID1 RAID10, 24 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD de 1Gbps até dezembro de graça quando pagar por um período de seis meses, você pode fazer o pedido aqui .

Dell R730xd 2 ? 2 Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 $249 ! . c Dell R730xd 5-2650 v4 9000 ?