Identifique fraudes usando o conjunto de dados da Enron. Parte 2, encontrando o melhor modelo

Apresento a você a segunda parte do artigo sobre a pesquisa de suspeita de fraude com base nos dados do Enron Dataset. Se você não leu a primeira parte, pode se familiarizar com ela aqui .

Agora falaremos sobre o processo de construção, otimização e escolha de um modelo que dê a resposta: vale a pena suspeitar de uma pessoa fraudulenta?

Antes, analisamos um dos conjuntos de dados abertos que fornece informações sobre suspeitos no caso Enron e fraudes nele. Além disso, o viés nos dados iniciais foi corrigido, lacunas (NaN) foram preenchidas, após o que os dados foram normalizados e a seleção dos atributos foi concluída.

O resultado foi familiar para muitos:

• X_train e y_train - a amostra usada para treinamento (111 registros);
• X_test e y_test - uma amostra na qual a exatidão das previsões de nossos modelos será verificada (28 entradas).

Falando de modelos ... Para prever corretamente se vale a pena suspeitar de uma pessoa, com base em alguns sinais que caracterizam suas atividades, usaremos a classificação. Os principais tipos de modelos usados ​​para resolver problemas nesse segmento podem ser obtidos no Sklearn:

• Naive Bayes (classificador ingênuo de Bayes);
• SVM (máquina de vetor de referência);
• K vizinhos mais próximos (método para encontrar vizinhos mais próximos);
• Floresta aleatória (floresta aleatória);
• Rede Neural.

Há também uma figura que ilustra muito bem sua aplicabilidade:

Entre eles, há uma Árvore de Decisão (árvore de decisão), familiar para muitos, mas, talvez, não faça sentido em uma tarefa usar esse método em conjunto com a Random Forest, que é um conjunto de árvores de decisão. Portanto, substitua-o por Regressão logística, que pode atuar como um classificador e produzir uma das opções esperadas (0 ou 1).

Iniciar

Inicializamos todos os classificadores mencionados com valores padrão:

from sklearn.naive_bayes import GaussianNB from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier from sklearn.svm import SVC from sklearn.neural_network import MLPClassifier from sklearn.ensemble import RandomForestClassifier random_state = 42 gnb = GaussianNB() svc = SVC() knn = KNeighborsClassifier() log = LogisticRegression(random_state=random_state) rfc = RandomForestClassifier(random_state=random_state) mlp = MLPClassifier(random_state=random_state) 

Também os agruparemos para que seja mais conveniente trabalhar com eles como um agregado, em vez de escrever código para cada indivíduo. Por exemplo, podemos treiná-los todos de uma vez:

 classifiers = [gnb, svc, knn, log, rfc, mlp] for clf in classifiers: clf.fit(X_train, y_train) 

Depois que os modelos foram treinados, chegou a hora do primeiro teste de sua qualidade de previsão. Além disso, visualizamos nossos resultados usando o Seaborn:

 from sklearn.metrics import accuracy_score def calculate_accuracy(X, y): result = pd.DataFrame(columns=['classifier', 'accuracy']) for clf in classifiers: predicted = clf.predict(X_test) accuracy = round(100.0 * accuracy_score(y_test, predicted), 2) classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') result = result.append({'classifier': classifier, 'accuracy': accuracy}, ignore_index=True) print('Accuracy is {accuracy}% for {classifier_name}'.format(accuracy=accuracy, classifier_name=classifier)) result = result.sort_values(['classifier'], ascending=True) plt.subplots(figsize=(10, 7)) sns.barplot(x="classifier", y='accuracy', palette=cmap, data=result) 

Vamos dar uma olhada na idéia geral da precisão dos classificadores:

 calculate_accuracy(X_train, y_train) 

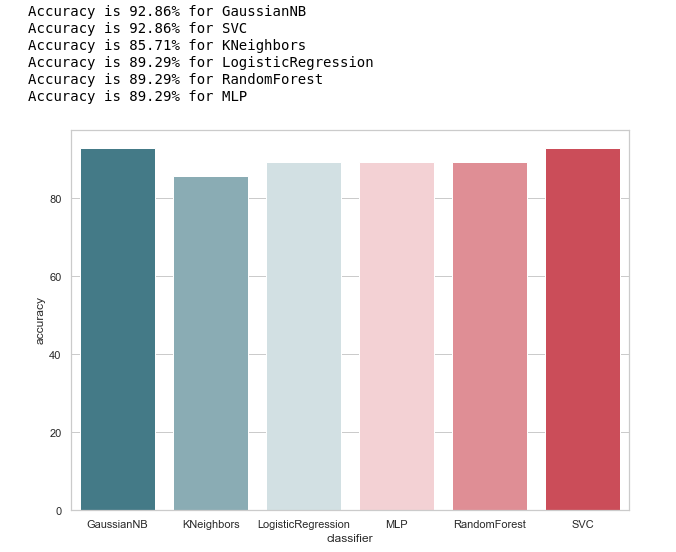
À primeira vista, parece muito bom, a precisão das previsões na amostra de teste flutua em torno de 90%. Parece que a tarefa é brilhante!

 def QuaziAlgo(features): return 0 

Mas, antes de nos lisonjear, vamos construir uma matriz de confusão para os resultados da previsão:

 from sklearn.metrics import confusion_matrix def make_confussion_matrices(X, y): matrices = {} result = pd.DataFrame(columns=['classifier', 'recall']) for clf in classifiers: classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') predicted = clf.predict(X_test) print(f'{predicted}-{classifier}') matrix = confusion_matrix(y_test,predicted,labels=[1,0]) matrices[classifier] = matrix.T return matrices 

Calculamos as matrizes de erro para cada classificador e, junto com isso, vemos o que eles previram:

 matrices = make_confussion_matrices(X_train,y_train) 

Mesmo uma representação textual do resultado do trabalho dos classificadores é suficiente para entender que algo claramente deu errado.

O método de vizinhos mais próximos não revelou um único suspeito na amostra de teste. Duas questões surgem:

1. Qual o motivo desse comportamento do classificador KNeighbors?
2. Por que criamos matrizes de erro se não as usamos, mas apenas observamos os resultados da previsão?

Dê uma olhada mais profunda

Vamos começar com a segunda pergunta. Vamos tentar visualizar nossas matrizes de erro e apresentar os dados em formato gráfico para entender onde ocorre o erro de classificação:

 import itertools from collections import Iterable def draw_confussion_matrices(row,col,matrices,figsize = (16,12)): fig, (axes) = plt.subplots(row,col, sharex='col', sharey='row',figsize=figsize ) if any(isinstance(i, Iterable) for i in axes): axes = list(itertools.chain.from_iterable(axes)) idx = 0 for name,matrix in matrices.items(): df_cm = pd.DataFrame( matrix, index=['True','False'], columns=['True','False'], ) ax = axes[idx] fig.subplots_adjust(wspace=0.1) sns.heatmap(df_cm, annot=True,cmap=cmap,cbar=False ,fmt="d",ax=ax,linewidths=1) ax.set_title(name) idx += 1 

Nós os exibimos em 2 linhas e 3 colunas:

 draw_confussion_matrices(2,3,matrices) 

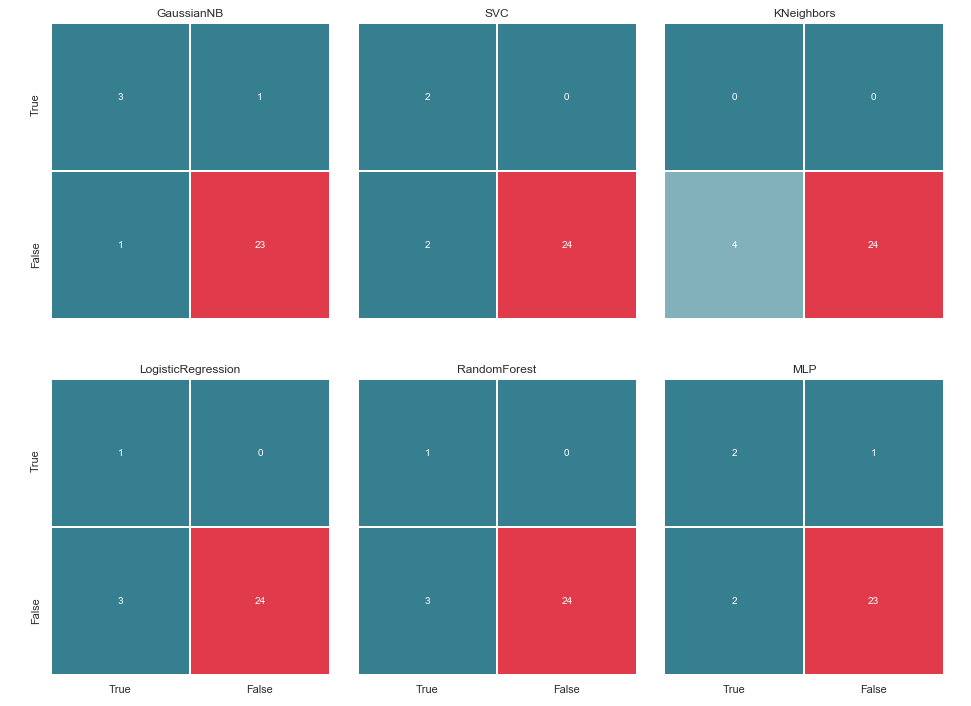
Antes de continuar, vale a pena dar alguns esclarecimentos. A designação True, localizada à esquerda da matriz de erros de um classificador específico, significa que o classificador considerou a pessoa suspeita, o valor False significa que a pessoa está além da suspeita. Da mesma forma Verdadeiro e Falso na parte inferior da imagem nos fornece um estado real de coisas, que pode não coincidir com a decisão do classificador.

Por exemplo, vemos que as decisões do KNeighbors com uma precisão de previsão de 85,71% coincidiram com o estado real das coisas quando 24 pessoas, por suspeita, foram incluídas em uma lista semelhante pelo classificador. Mas 4 pessoas da lista de suspeitos também foram incluídas nesta lista. Se esse classificador tomasse decisões, talvez alguém pudesse ter evitado o tribunal.

Assim, as matrizes de erro são uma ferramenta muito boa para entender o que deu errado nos problemas de classificação. Sua principal vantagem é a visibilidade e, portanto, apelamos a eles.

Métricas

Em termos gerais, isso pode ser ilustrado pela figura a seguir:

E o que é TP, TN, FP e algum tipo de FN neste caso?

$$$TP \ - \ verdadeiro positivo \ solução \\ TN \ - \ verdadeiro negativo \ solução \\ FP \ - \ falso positivo \ solução \\ FN \ - \ falso negativo \ solução$

Em outras palavras, nos esforçamos para garantir que as respostas do classificador e o estado real das coisas coincidam. Ou seja, para garantir que todos os números sejam distribuídos entre as células TP e TN (soluções verdadeiras) e não caiam em FN e FP (soluções falsas).

E como estamos falando de abreviações, é hora de recuperar as métricas de precisão (Precisão) e integridade (Rechamada).

Se você sair do registro formal, o Precision poderá ser expresso como:

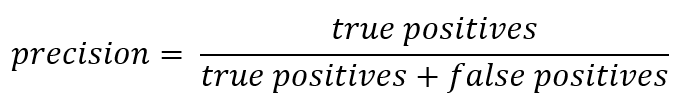
Em outras palavras, é mantida uma conta de quantas respostas positivas recebidas do classificador estão corretas. Quanto maior a precisão, menor o número de acertos falsos (a precisão é 1 se não houver FPs).

Lembre- se geralmente é apresentado como:

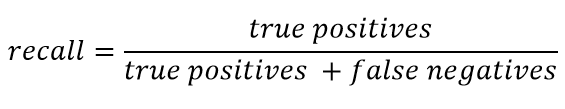
Lembre-se de caracterizar a capacidade do classificador de "adivinhar" o maior número possível de respostas positivas. Quanto maior a integridade, menor o FN.

Geralmente eles tentam se equilibrar entre os dois, mas, neste caso, a prioridade será completamente dada ao Precision. O motivo: uma abordagem mais humanística, o desejo de minimizar o número de falsos positivos e, como resultado, evitar que as suspeitas caiam sobre os inocentes.

Calculamos a precisão para nossos classificadores:

 from sklearn.metrics import precision_score def calculate_precision(X, y): result = pd.DataFrame(columns=['classifier', 'precision']) for clf in classifiers: predicted = clf.predict(X_test) precision = precision_score(y_test, predicted, average='macro') classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') result = result.append({'classifier': classifier, 'precision': precision}, ignore_index=True) print('Precision is {precision} for {classifier_name}'.format(precision=round(precision,2), classifier_name=classifier)) result = result.sort_values(['classifier'], ascending=True) plt.subplots(figsize=(10, 7)) sns.barplot(x="classifier", y='precision', palette=cmap, data=result) calculate_precision(X_train, y_train) 

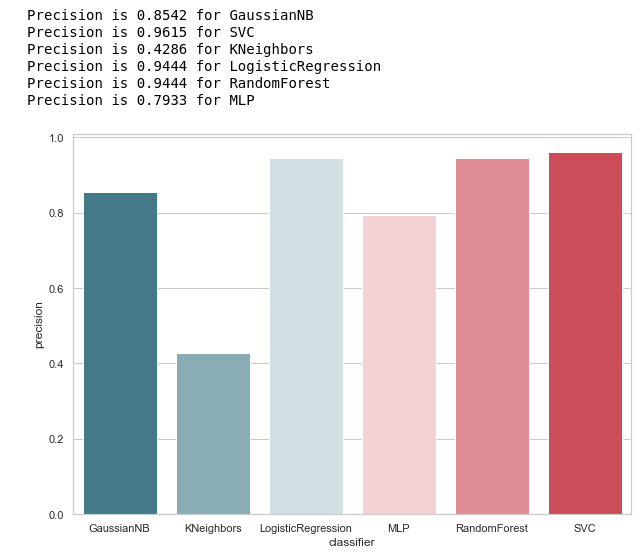
Como segue a figura, saiu como esperado: a precisão do KNeighbors acabou sendo a mais baixa, porque o valor de TP é o mais baixo.

Ao mesmo tempo, há um bom artigo sobre métricas no Habré, e quem quiser se aprofundar mais neste tópico deve se familiarizar com ele.

Seleção de parâmetros de hiper

Depois de encontrarmos a métrica que melhor se adapta às condições selecionadas (reduzimos o número de FPs), podemos voltar à primeira pergunta: Qual é a razão desse comportamento do classificador KNeighbors?

O motivo está nas configurações padrão com as quais este modelo foi criado. E, provavelmente, muitos poderiam exclamar a esta etapa: por que treinar em parâmetros padrão? Existem ferramentas de seleção especiais, por exemplo, o GridSearchCV frequentemente usado.
Sim, é, e chegou a hora de recorrer a isso,

Mas antes disso, removemos o classificador bayesiano da nossa lista. Ele permite um FP e, ao mesmo tempo, esse algoritmo não aceita parâmetros variáveis, pelo que o resultado não será alterado.

 classifiers.remove(gnb) 

Ajuste fino

Definimos uma grade de parâmetros para cada classificador:

 parameters = {'SVC':{'kernel':('linear', 'rbf','poly'), 'C':[i for i in range(1,11)],'random_state': (random_state,)}, 'KNeighbors':{'algorithm':('ball_tree', 'kd_tree'), 'n_neighbors':[i for i in range(2,20)]}, 'LogisticRegression':{'penalty':('l1', 'l2'), 'C':[i for i in range(1,11)],'random_state': (random_state,)}, 'RandomForest':{'n_estimators':[i for i in range(10,101,10)],'random_state': (random_state,)}, 'MLP':{'activation':('relu','logistic'),'solver':('sgd','lbfgs'),'max_iter':(500,1000), 'hidden_layer_sizes':[(7,),(7,7)],'random_state': (random_state,)}} 

Além disso, eu queria prestar atenção ao número de camadas / neurônios no MLP.
Decidiu defini-los não pela pesquisa exaustiva de todos os valores possíveis, mas ainda basear-se na fórmula :

$$$N_h = \ frac {N_s} {(\ alpha * (N_i + N_o))} = \ frac {117} {(2 * (7 + 1))} \ aproximadamente 7$

Quero dizer imediatamente que o treinamento e a validação cruzada serão realizados apenas na amostra de treinamento. Suponho que exista uma opinião de que você pode fazer isso em todos os dados, como no exemplo do Iris Dataset. Mas, na minha opinião, essa abordagem não é totalmente justificada, pois não será possível confiar nos resultados da verificação em uma amostra de teste.

Realizaremos a otimização e substituiremos nossos classificadores por sua versão aprimorada:

 from sklearn.model_selection import GridSearchCV warnings.filterwarnings('ignore') for idx,clf in enumerate(classifiers): classifier = clf.__class__.__name__ classifier = classifier.replace('Classifier', '') params = parameters.get(classifier) if not params: continue new_clf = clf.__class__() gs = GridSearchCV(new_clf, params, cv=5) result =gs.fit(X_train, y_train) print(f'The best params for {classifier} are {result.best_params_}') classifiers[idx] = result.best_estimator_ 

Depois de escolhermos uma métrica para avaliação e executarmos o GridSearchCV, estamos prontos para desenhar a linha final.

Resumir

Matriz de erro v.2

 matrices = make_confussion_matrices(X_train,y_train) draw_confussion_matrices(1,2,first_row,figsize = (10.5,6)) draw_confussion_matrices(1,3,second_row,figsize = (16,6)) 

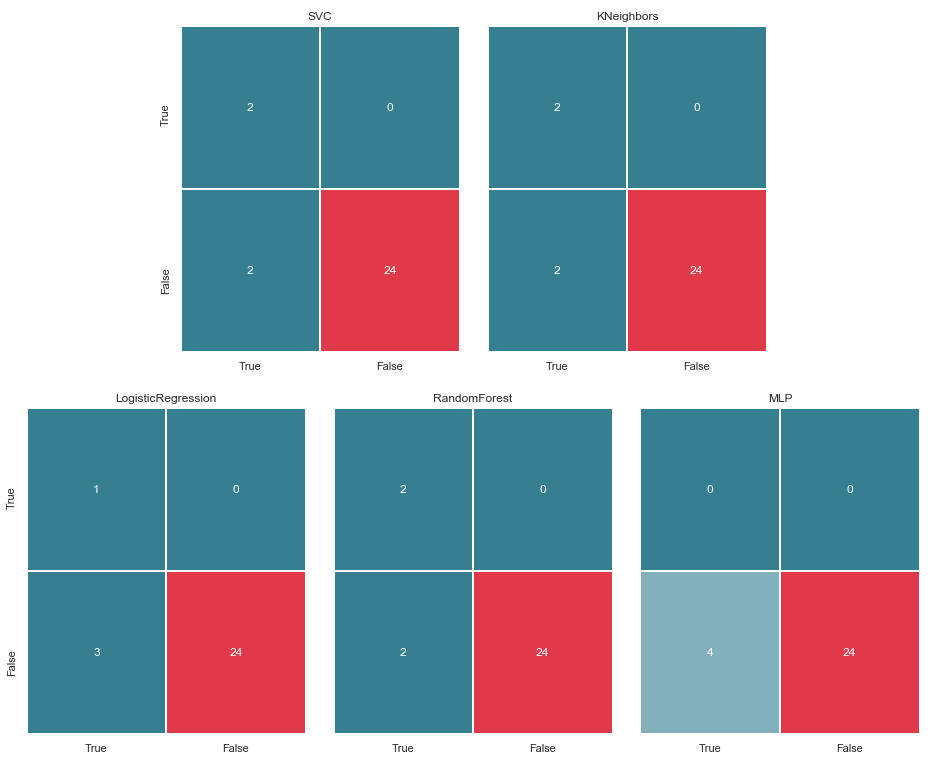
Como pode ser visto na matriz, o MLP mostrou degradação e considerou que não havia suspeitos na amostra de teste. A Random Forest ganhou precisão e corrigiu os parâmetros para Falso Negativo e Verdadeiro Positivo. E o KNeighbors mostrou uma melhoria na previsão. A previsão para outros não mudou.

Precisão v.2

Agora, nenhum dos nossos classificadores atuais apresenta erros no Falso Positivo, o que é uma boa notícia. Mas, se expressarmos tudo na linguagem dos números, obteremos a seguinte imagem:

 calculate_precision(X_train, y_train) 

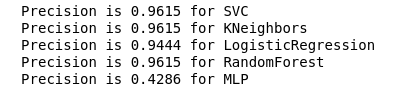
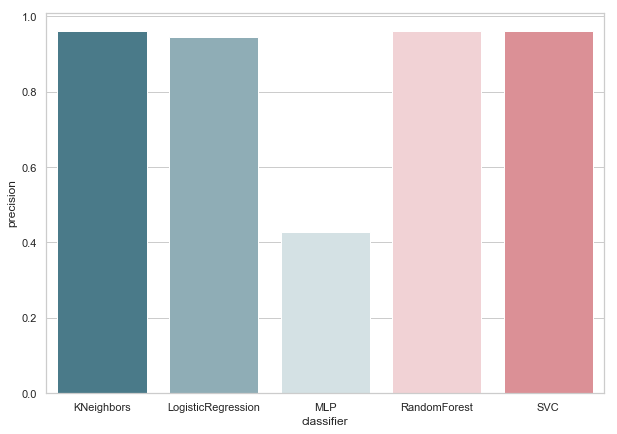
Foram identificados três classificadores com a maior pontuação de precisão. E eles têm os mesmos valores, com base na matriz de erros. Qual classificador escolher?

Quem é melhor?

Parece-me que essa é uma pergunta bastante difícil para a qual não há resposta universal. No entanto, meu ponto de vista neste caso seria algo como isto:

1. O classificador deve ser o mais simples possível na sua implementação técnica. Então ele terá menos risco de reciclagem (provavelmente isso aconteceu com o MLP). Portanto, essa não é uma floresta aleatória, pois esse algoritmo é um conjunto de 30 árvores e, como resultado, depende delas. Em consonância com uma das idéias do Python Zen: simples é melhor que complexo.

2. Nada mal quando o algoritmo foi intuitivo. Ou seja, o KNeighbors é percebido de maneira mais simples que os SVMs com potencial espaço multidimensional.
Que, por sua vez, é semelhante a outra declaração: explícito é melhor que implícito.

Portanto, o KNeighbors com 3 vizinhos, na minha opinião, é o melhor candidato.

Este é o fim da segunda parte, descrevendo o uso do Enron Dataset como um exemplo da tarefa de classificação no aprendizado de máquina. Com base nos materiais do curso Introdução ao aprendizado de máquina sobre Udacity. Há também um notebook python refletindo toda a sequência de ações descrita.