Teoria dos Jogos: Tomada de Decisão com Exemplos no Kotlin

A teoria dos jogos é uma disciplina matemática que considera modelar as ações dos jogadores que têm um objetivo, que é escolher as estratégias ideais para o comportamento em um conflito. Em Habré, esse tópico já foi abordado , mas hoje falaremos sobre alguns de seus aspectos em mais detalhes e consideraremos exemplos no Kotlin.

Portanto, uma estratégia é um conjunto de regras que determinam a escolha de um curso de ação para cada movimento pessoal, dependendo da situação. A estratégia ideal para o jogador é a estratégia que garante a melhor posição em um determinado jogo, ou seja, ganho máximo. Se o jogo for repetido várias vezes e contiver, além de jogadas aleatórias e pessoais, a estratégia ideal fornecerá a média máxima de vitórias.

A tarefa da teoria dos jogos é identificar as estratégias ideais para os jogadores. A principal premissa, com base nas estratégias ideais, é que o oponente (ou oponentes) não é menos inteligente que o próprio jogador e faz tudo para alcançar seu objetivo. O cálculo de um oponente razoável é apenas uma das posições em potencial no conflito, mas, na teoria dos jogos, é o que está estabelecido na base.

Existem jogos com a natureza em que há apenas um participante maximizando seus lucros. Jogos com a natureza são modelos matemáticos nos quais a escolha da solução depende da realidade objetiva. Por exemplo, demanda do consumidor, estado da natureza etc. "Natureza" é um conceito generalizado de adversário que não persegue seus próprios objetivos. Nesse caso, vários critérios são usados ​​para selecionar a estratégia ideal.
Existem dois tipos de tarefas em jogos com a natureza:

1. a tarefa de tomar decisões em condições de risco quando forem conhecidas as probabilidades com as quais a natureza aceita cada um dos estados possíveis;
2. tarefas de tomada de decisão em condições de incerteza, quando não é possível obter informações sobre as probabilidades de ocorrência de estados da natureza.

Brevemente sobre esses critérios é descrito aqui .

Agora, consideraremos os critérios de tomada de decisão em estratégias puras e, no final do artigo, resolveremos o jogo em estratégias mistas pelo método analítico.

Declaração do problema

Analisaremos todos os critérios de tomada de decisão usando um exemplo completo. A tarefa é a seguinte: o agricultor precisa determinar em que proporções semear seu campo com três culturas, se o rendimento dessas culturas e, portanto, o lucro, depende de como será o verão: frio e chuvoso, normal ou quente e seco. O agricultor calculou o lucro líquido de 1 hectare de diferentes culturas, dependendo do clima. O jogo é determinado pela seguinte matriz:



Além disso, apresentaremos essa matriz na forma de estratégias:

$$

$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$$

A estratégia ideal desejada é indicada por $$$u_ {opt}$ . Vamos resolver o jogo usando os critérios de Wald, otimismo, pessimismo, Savage e Hurwitz em condições de incerteza e os critérios de Bayes e Laplace em condições de risco.

Como mencionado acima, os exemplos estarão no Kotlin. Observo que, em geral, existem soluções como Gambit (escrita em C), Axelrod e PyNFG (escrita em Python), mas montaremos nossa própria bicicleta, montada no joelho, apenas para mostrar um pouco de estilo, moda e estilo. linguagem de programação juvenil.

Para implementar programaticamente a solução do jogo, apresentaremos várias classes. Primeiro, precisamos de uma classe que nos permita descrever uma linha ou coluna de uma matriz de jogo. A classe é extremamente simples e contém uma lista de valores possíveis (alternativas ou estados da natureza) e seu nome correspondente. O campo- key será usado para identificação, bem como para comparação, e a comparação será necessária na implementação da dominação.


A matriz do jogo contém informações sobre alternativas e estados da natureza. Além disso, implementa alguns métodos, por exemplo, encontrar o conjunto dominante e o preço líquido do jogo.


Descrevemos a interface que atende aos critérios

Tomada de decisão sob incerteza

Tomar decisões diante da incerteza sugere que o jogador não se opõe a um oponente razoável.

Critério Wald

O critério Wald maximiza o pior resultado possível:

$$

$$u_ {opt} = max_ {i} min_ {j} [U]$$

O uso do critério garante o pior resultado, mas o preço dessa estratégia é a perda da oportunidade de obter o melhor resultado possível.

Considere um exemplo. Para estratégias $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ encontre os pontos baixos e obtenha os próximos três $$$S = (0, 1, -1)$ . O máximo para o triplo indicado será o valor 1, portanto, de acordo com o critério de Wald, a estratégia vencedora é a estratégia $$$U_ {2} = (2,3,1)$ correspondente à cultura de plantio 2.

A implementação do software do critério Wald é simples:

 class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } } 

Por uma questão de clareza, pela primeira vez, mostrarei como a solução se pareceria com um teste:


É fácil adivinhar que, para outros critérios, a diferença estará apenas na criação do objeto de criteria .

Critério de otimismo

Ao usar o critério de um otimista, o jogador escolhe uma solução que dê o melhor resultado, enquanto o otimista assume que as condições do jogo serão mais favoráveis ​​para ele:

$$

$$u_ {opt} = max_ {i} max_ {j} [U]$$

A estratégia de um otimista pode levar a consequências negativas quando a oferta máxima coincide com a demanda mínima - a empresa pode receber perdas ao anular produtos não vendidos. Ao mesmo tempo, a estratégia do otimista tem um certo significado, por exemplo, você não precisa cuidar de clientes insatisfeitos, pois qualquer demanda possível é sempre atendida, portanto, não há necessidade de manter a localização do cliente. Se a demanda máxima for atingida, a estratégia do otimista permitirá obter o máximo de utilidade, enquanto outras estratégias levarão a lucros perdidos. Isso oferece certas vantagens competitivas.

Considere um exemplo. Para estratégias $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ encontre, encontre o máximo e obtenha os próximos três $$$S = (5, 3, 4)$ . O máximo para o triplo indicado será o valor 5, portanto, de acordo com o critério de otimismo, a estratégia vencedora é a estratégia $$$U_ {1} = (0,2,5)$ correspondente à cultura de plantio 1.

A implementação do critério de otimismo quase não difere do critério de Wald

 class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } } 

Critério de pessimismo

Este critério visa selecionar o menor elemento da matriz do jogo dentre seus elementos mínimos possíveis:

$$

$$u_ {opt} = min_ {i} min_ {j} [U]$$

O critério do pessimismo sugere que o desenvolvimento de eventos será desfavorável para o tomador de decisão. Ao usar esse critério, o tomador de decisão é guiado pela possível perda de controle sobre a situação; portanto, ele tenta excluir riscos em potencial escolhendo a opção com rentabilidade mínima.

Considere um exemplo. Para estratégias $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ encontre, encontre o mínimo e obtenha os próximos três $$$S = (0, 1, -1)$ . O mínimo para o triplo indicado será -1, portanto, de acordo com o critério do pessimismo, a estratégia vencedora é a estratégia $$$U_ {3} = (4,3, -1)$ correspondente à cultura de plantio 3.

Depois de conhecer os critérios e o otimismo de Wald, é fácil adivinhar como será a classe do critério de pessimismo:

 class PessimismCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val min = mins.minWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == min!!.second } .map { m -> m.first } } } 

Critério selvagem

O critério Savage (critério de um pessimista pessimista) envolve minimizar os maiores lucros perdidos; em outras palavras, o maior arrependimento pelos lucros perdidos é minimizado:

$$

$$u_ {opt} = min_ {i} max_ {j} [S] \\ s_ {i, j} = (max \ begin {bmatrix} u_ {1, j} \\ u_ {2, j} \\. .. \\ u_ {n, j} \ end {bmatrix} - u_ {i, j})$$

Nesse caso, S é a matriz de arrependimentos.

A solução ideal de acordo com o critério Savage deve apresentar o mínimo arrependimento dos arrependimentos encontrados na etapa anterior. A solução correspondente ao utilitário encontrado será ideal.

Os recursos da solução obtida incluem uma ausência garantida das maiores decepções e uma diminuição garantida no número máximo de vitórias possíveis de outros jogadores.

Considere um exemplo. Para estratégias $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ faça uma matriz de arrependimentos:



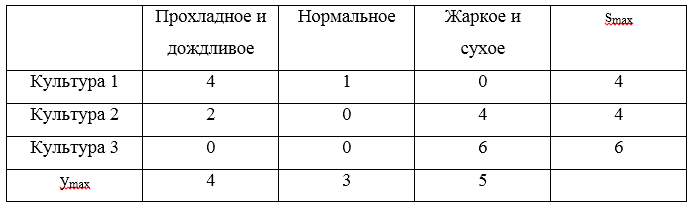
Três arrependimentos máximos $$$S = (4,4,6)$ . O valor mínimo desses riscos será 4, o que corresponde às estratégias $$$U_ {1}$ e $$$U_ {2}$ .

Programar o teste Savage é um pouco mais difícil:

 class SavageCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.risk(): List<Pair<GameVector, Double?>> { val maxStates = this.natureStates.map { n -> Pair(n, n.values.max()) } .map { n -> n.first.key to n.second }.toMap() var am: MutableList<Pair<GameVector, List<Double>>> = mutableListOf() for (a in this.alternatives) { var v: MutableList<Double> = mutableListOf() for (i in 0..a.values.lastIndex) { val mn = maxStates.get(i) v.add(mn!! - a.values[i]) } am.add(Pair(a, v.toList())) } return am.map { m -> Pair(m.first, m.second.max()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.risk() val minRisk = risk.minWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == minRisk!!.second } .map { m -> m.first } } } 

Critério de Hurwitz

O critério Hurwitz é um compromisso regulamentado entre extremo pessimismo e completo otimismo:

$$

$$u_ {opt} = max (\ gama × A (k) + A (0) × (1 - \ gama))$$

A (0) é a estratégia do pessimista extremo, A (k) é a estratégia do otimista completo, $$$\ gama = 1$ - valor definido do coeficiente de peso: $$$0 \ leq \ gama \ leq1$ ; $$$\ gama = 0$ - pessimismo extremo, $$$\ gama = 1$ - otimismo total.

Com um pequeno número de estratégias discretas, definir o valor desejado do coeficiente de peso $$$\ gama$ e, em seguida, arredonde o resultado para o valor mais próximo possível, levando em consideração a discretização realizada.

Considere um exemplo. Para estratégias $$$U_ {1} = (0,2,5), U_ {2} = (2,3,1), U_ {3} = (4,3, -1)$ . Assumimos que o coeficiente de otimismo $$$\ gama = $ 0,$ . Agora faça uma mesa:



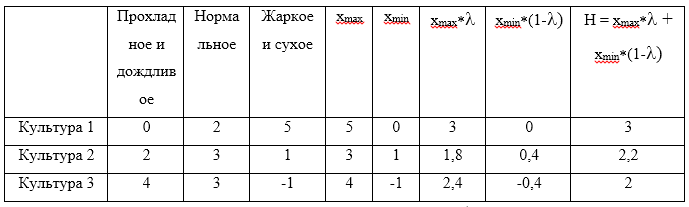
O valor máximo do H calculado será o valor 3, que corresponde à estratégia $$$U_ {1}$ .

A implementação do critério Hurwitz já é mais volumosa:

 class HurwitzCriteria(gameMatrix: GameMatrix, optimisticKoef: Double) : ICriteria { val gameMatrix: GameMatrix val optimisticKoef: Double init { this.gameMatrix = gameMatrix this.optimisticKoef = optimisticKoef } inner class HurwitzParam(xmax: Double, xmin: Double, optXmax: Double){ val xmax: Double val xmin: Double val optXmax: Double val value: Double init{ this.xmax = xmax this.xmin = xmin this.optXmax = optXmax value = xmax * optXmax + xmin * (1 - optXmax) } } fun GameMatrix.getHurwitzParams(): List<Pair<GameVector, HurwitzParam>> { return this.alternatives.map { a -> Pair(a, HurwitzParam(a.max()!!, a.min()!!, optimisticKoef)) } } override fun optimum(): List<GameVector> { val hpar = gameMatrix.getHurwitzParams() val maxHurw = hpar.maxWith(Comparator { o1, o2 -> o1.second.value.compareTo(o2.second.value) }) return hpar .filter { r -> r.second == maxHurw!!.second } .map { m -> m.first } } } 

Tomada de decisão em risco

Os métodos de tomada de decisão podem se basear em critérios para tomada de decisão em condições de risco, sujeitas às seguintes condições:

• falta de informações confiáveis ​​sobre as possíveis consequências;
• a presença de distribuições de probabilidade;
• conhecimento da probabilidade de resultados ou consequências para cada decisão.

Se uma decisão é tomada sob condições de risco, os custos de decisões alternativas são descritos por distribuições de probabilidade. Nesse sentido, a decisão se baseia no uso do critério de valor esperado, segundo o qual soluções alternativas são comparadas em termos de maximizar lucros esperados ou minimizar custos esperados.

O critério do valor esperado pode ser reduzido para maximizar o lucro (médio) esperado ou para minimizar os custos esperados. Nesse caso, supõe-se que o lucro (custos) associado a cada solução alternativa seja uma variável aleatória.

A formulação de tais tarefas é geralmente a seguinte: uma pessoa escolhe qualquer ação em uma situação em que eventos aleatórios influenciam o resultado da ação. Mas o jogador tem algum conhecimento sobre as probabilidades desses eventos e pode calcular a combinação e sequência mais lucrativas de suas ações.

Para continuar a dar exemplos, complementamos a matriz do jogo com probabilidades:



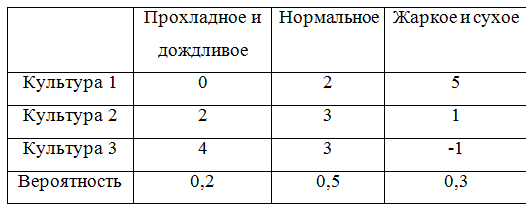
Para levar em conta as probabilidades, uma classe que descreve a matriz do jogo precisará ser refeita um pouco. Acabou, na verdade, não muito elegante, mas tudo bem.

Critério de Bayes

O critério de Bayes (critério de expectativa) é usado nos problemas de tomada de decisão em condições de risco como uma avaliação da estratégia $$$u_ {i}$ a expectativa matemática da variável aleatória correspondente aparece. De acordo com essa regra, a estratégia ideal do jogador $$$u_ {opt}$ é encontrado a partir da condição:

$$

$$u_ {opt} = max_ {1 \ leq i \ leq n} M (u_ {i}) \\ M (u_ {i}) = max_ {1 \ leq i \ leq n} \ sum_ {j = 1} ^ m u_ {i, j} \ cdot y_ {j} ^ 0$$

Em outras palavras, um indicador de ineficiência da estratégia $$$u_ {i}$ pelo critério de Bayes em relação aos riscos é o valor médio (expectativa) dos riscos da i-ésima linha da matriz $$$U$ cujas probabilidades coincidem com as probabilidades da natureza. Então, o ideal entre estratégias puras pelo critério de Bayes em relação aos riscos é a estratégia $$$u_ {opt}$ com ineficiência mínima, ou seja, risco médio mínimo. O critério bayesiano é equivalente em relação aos ganhos e em relação aos riscos, ou seja, se a estratégia $$$u_ {opt}$ é ideal pelo critério de Bayes em relação às vitórias, então é ideal pelo critério de Bayes em relação aos riscos e vice-versa.

Vamos seguir para o exemplo e calcular as expectativas matemáticas:

$$

$$M_1 = 0 \ cdot0.2 +2 \ cdot0.5 +5 \ cdot0.3 = 2.5; \\ M_2 = 2 \ cdot0.2 +3 \ cdot0.5 +1 \ cdot0.3 = 2.2 ; \\ M_4 = 0 \ cdot0.2 +3 \ cdot0.5 + (- 1) \ cdot0.3 = 2.0;$$

A expectativa matemática máxima é $$$M_1$ portanto, uma estratégia vencedora é uma estratégia $$$U_1$ .

Implementação de software do critério Bayes:

 class BayesCriteria(gameMatrix: ProbabilityGameMatrix) : ICriteria { val gameMatrix: ProbabilityGameMatrix init { this.gameMatrix = gameMatrix } fun ProbabilityGameMatrix.bayesProbability(): List<Pair<GameVector, Double?>> { var am: MutableList<Pair<GameVector, Double>> = mutableListOf() for (a in this.alternatives) { var alprob: Double = 0.0 for (i in 0..a.values.lastIndex) { alprob += a.values[i] * this.probabilities[i] } am.add(Pair(a, alprob)) } return am.toList(); } override fun optimum(): List<GameVector> { val risk = gameMatrix.bayesProbability() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } } 

Critério de Laplace

O critério de Laplace apresenta uma maximização simplificada da expectativa matemática de utilidade quando é válida a suposição de igual probabilidade de níveis de demanda, o que elimina a necessidade de coletar estatísticas reais.

No caso geral, ao usar o critério de Laplace, a matriz de utilidades esperadas e o critério ideal são determinados da seguinte forma:

$$

$$u_ {opt} = max [\ overline {U}] \\ \ overline {U} = \ begin {bmatrix} \ overline {u} _ {1} \\ \ overline {u} _ {2} \\. .. \\ \ overline {u} _ {n} \ end {bmatrix}, \ overline {u} _ {i} = \ frac {1} {n} \ sum_ {j = 1} ^ nu_ {i, j }$$

Considere o exemplo de tomada de decisão pelo critério de Laplace. Calculamos a média aritmética de cada estratégia:

$$

$$\ overline {u} _ {1} = \ frac {1} {3} \ cdot (0 + 2 + 5) = 2,3 \\ \ overline {u} _ {2} = \ frac {1} { 3} \ cdot (2 + 3 + 1) = 2,0 \\ \ overline {u} _ {3} = \ frac {1} {3} \ cdot (4 + 3-1) = $ 2,$$

Então a estratégia vencedora é a estratégia $$$U_1$ .

Implementação de software do critério de Laplace:

 class LaplaceCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.arithemicMean(): List<Pair<GameVector, Double>> { return this.alternatives.map { m -> Pair(m, m.values.average()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.arithemicMean() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second.compareTo(o2.second) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } } 

Estratégias mistas. Método analítico

O método analítico permite resolver o jogo em estratégias mistas.Para formular um algoritmo para encontrar uma solução para um jogo por um método analítico, consideramos alguns conceitos adicionais.

Estratégia$$A L i estratégia dominado$U_{i}$$$U i - 1 , se todos$U_{i-1}$$$$u_{1..n} \in U_{i} \geq u_{1..n} \in U_{i-1}$ .Em outras palavras, se em uma linha de uma matriz de pagamento todos os elementos forem maiores ou iguais aos elementos correspondentes de outra linha, a primeira linha dominará a segunda e será chamada de linha dominante. E também, se em alguma coluna da matriz de pagamento todos os elementos forem menores ou iguais aos elementos correspondentes de outra coluna, a primeira coluna domina a segunda e é chamada de coluna dominante.

O preço mais baixo do jogo é chamado$$$\alpha = max_i min_j u_{ij}$ .
O preço mais alto do jogo é chamado $$$\beta = min_j max_i u_{ij}$ .

Agora você pode formular um algoritmo para resolver o jogo pelo método analítico:

1. Calcular o fundo $$α e superior$\alpha$$$β preços dos jogos. Se$\beta$$$α = β , então escreva a resposta em estratégias puras; caso contrário, continue a solução$\alpha = \beta$
2. Exclua linhas dominantes colunas dominantes. Pode haver vários. Em seu lugar na estratégia ideal, os componentes correspondentes serão 0
3. Resolva o jogo da matriz por programação linear.

Para dar um exemplo, você precisa dar uma classe que descreva a solução


E a classe que executa a solução pelo método simplex. Como não entendo matemática, usei a implementação pronta do Apache Commons Math


Agora, executamos a solução pelo método analítico. Para maior clareza, adotamos outra matriz de jogo:

$$

$$\begin{pmatrix} 2& 4& 8& 5 \\ 6& 2& 4& 6\\ 3& 2& 5& 4 \end{pmatrix}$$

Existe um conjunto dominante nessa matriz:
$$\begin{pmatrix} 2& 4\\ 6& 2\end{pmatrix}$$

Solução de jogo $$( 0 , 33 ; 0 , 67 ; 0 ) com o preço do jogo igual a 3,33$(0,33; 0,67; 0)$

Em vez de uma conclusão

Espero que este artigo seja útil para quem precisa de uma primeira aproximação com a solução de jogos com a natureza. Em vez de conclusões, um link para o GitHub .

Ficaria muito grato pelo feedback construtivo!