Olá Habr! Apresento a vocês a primeira página do Solving bandits multiarmed: Uma comparação entre o artigo epsilon-greedy e Thompson .

O problema dos bandidos armados

O problema dos bandidos com várias armas é uma das tarefas mais básicas na ciência das soluções. Ou seja, esse é o problema da alocação ótima de recursos em condições de incerteza. O nome "bandido multi-armado" veio das antigas máquinas caça-níqueis controladas por alças. Esses rifles de assalto foram apelidados de "bandidos", porque depois de conversar com eles, as pessoas geralmente se sentiam assaltadas. Agora imagine que existem várias dessas máquinas e a chance de ganhar contra carros diferentes é diferente. Desde que começamos a brincar com essas máquinas, queremos determinar qual chance é maior e usar essa máquina com mais frequência do que outras.

O problema é o seguinte: como podemos entender com mais eficiência qual máquina é mais adequada e, ao mesmo tempo, experimentar muitos recursos em tempo real? Este não é um tipo de problema teórico, é um problema que uma empresa enfrenta o tempo todo. Por exemplo, uma empresa possui várias opções de mensagens que precisam ser exibidas aos usuários (por exemplo, as mensagens incluem anúncios, sites, imagens) para que as mensagens selecionadas maximizem uma determinada tarefa comercial (conversão, clicabilidade etc.)

Uma maneira típica de resolver esse problema é executar testes A / B várias vezes. Ou seja, por várias semanas para mostrar cada uma das opções com a mesma frequência e, com base em testes estatísticos, decida qual opção é melhor. Esse método é adequado quando há poucas opções, por exemplo, 2 ou 4. Mas quando há muitas opções, essa abordagem se torna ineficaz - tanto no tempo perdido quanto no lucro perdido.

A origem do tempo perdido deve ser fácil de entender. Mais opções - são necessários mais testes A / B - é necessário mais tempo para tomar uma decisão. A ocorrência de lucros perdidos não é tão óbvia. Perda de oportunidade (custo de oportunidade) - os custos associados ao fato de que, em vez de uma ação, realizamos outra, ou seja, em termos simples, é isso que perdemos investindo em A em vez de B. Investir em B é o lucro perdido de investir em A. O mesmo com a opção de verificação. Os testes A / B não devem ser interrompidos até que sejam concluídos. Isso significa que o pesquisador não sabe qual opção é melhor até o teste terminar. No entanto, acredita-se que uma opção seja melhor que a outra. Isso significa que, prolongando os testes A / B, não mostramos as melhores opções para um número suficientemente grande de visitantes (embora não saibamos quais são as melhores), perdendo assim nosso lucro. Esse é o benefício perdido dos testes A / B. Se houver apenas um teste A / B, talvez o lucro perdido não seja nada bom. Um grande número de testes A / B significa que, por um longo tempo, temos que mostrar aos clientes muitas das melhores opções. Seria melhor se você pudesse rapidamente jogar fora as opções ruins em tempo real e, somente então, quando houver poucas opções, use os testes A / B para elas.

Samplers ou agentes são maneiras de testar e otimizar rapidamente a distribuição de opções. Neste artigo, apresentarei a amostragem Thompson e suas propriedades. Também compararei a amostragem de Thompson com o algoritmo épsilon-ganancioso, outra opção popular para o problema de bandidos com várias armas. Tudo será implementado no Python do zero - todo o código pode ser encontrado aqui .

Breve Dicionário de Conceitos

Agente, amostrador, bandido ( agente, amostrador, bandido ) - um algoritmo que toma decisões sobre qual opção exibir.
Variante - uma variante diferente da mensagem que o visitante vê.
Ação - a ação que o algoritmo escolheu (qual opção mostrar).
Usar ( explorar ) - faça uma escolha para maximizar a recompensa total com base nos dados disponíveis.
Explorar, explorar - faça escolhas para entender melhor o retorno de cada opção.
Prêmio, pontos ( pontuação, recompensa ) - uma tarefa comercial, por exemplo, conversão ou clicabilidade. Por uma questão de simplicidade, acreditamos que ele é distribuído binomialmente e é igual a 1 ou 0 - clicou ou não.
Ambiente - o contexto em que o agente opera - opções e seu "retorno" oculto para o usuário.
Payback, probabilidade de sucesso ( taxa de pagamento ) - uma variável oculta igual à probabilidade de obter pontuação = 1, para cada opção é diferente. Mas o usuário não a vê.
Try ( avaliação ) - o usuário visita a página.
Lamento é a diferença entre qual seria o melhor resultado de todas as opções disponíveis e qual foi o resultado da opção disponível na tentativa atual. Quanto menos se arrepender das ações já tomadas, melhor.
Mensagem ( mensagem ) - um banner, opção de página e mais versões diferentes das quais queremos experimentar.
Amostragem - a geração de uma amostra a partir de uma determinada distribuição.

Explorar e explorar

Os agentes são algoritmos que procuram uma abordagem para a tomada de decisões em tempo real, a fim de alcançar um equilíbrio entre explorar o espaço de opções e usar a melhor opção. Esse equilíbrio é muito importante. O espaço das opções deve ser investigado para se ter uma idéia de qual opção é a melhor. Se descobrimos pela primeira vez essa opção ideal e a usamos o tempo todo, maximizaremos a recompensa total que está disponível para nós do ambiente. Por outro lado, também queremos explorar outras opções possíveis - e se elas se tornarem melhores no futuro, mas ainda não sabemos? Em outras palavras, queremos garantir possíveis perdas, tentando experimentar um pouco de opções abaixo do ideal para esclarecer por si mesmas o seu retorno. Se o retorno deles for realmente maior, eles poderão ser mostrados com mais frequência. Outra vantagem das opções de exploração é que podemos entender melhor não apenas o retorno médio, mas também o quanto o retorno é distribuído, ou seja, podemos estimar melhor a incerteza.
O principal problema, portanto, é resolver - qual é a melhor saída do dilema entre exploração e exploração (tradeoff exploração-exploração).

Algoritmo Epsilon-ganancioso

Uma saída típica desse dilema é o algoritmo epsilon-ganancioso. "Ganancioso" significa exatamente o que você pensou. Após um período inicial, quando acidentalmente fazemos tentativas - digamos, 1000 vezes, o algoritmo escolhe ansiosamente a melhor opção k em e por cento das tentativas. Por exemplo, se e = 0,05, o algoritmo 95% do tempo seleciona a melhor opção e, nos 5% restantes, seleciona tentativas aleatórias. De fato, este é um algoritmo bastante eficaz, no entanto, pode não ser suficiente explorar o espaço de opções e, portanto, não será bom o suficiente avaliar qual opção é a melhor para ficar preso a uma opção abaixo do ideal. Vamos mostrar no código como esse algoritmo funciona.

Mas primeiro, algumas dependências. Nós devemos definir o ambiente. Este é o contexto no qual os algoritmos serão executados. Nesse caso, o contexto é muito simples. Ele chama o agente para que ele decida qual ação escolher; o contexto inicia essa ação e retorna os pontos recebidos para ela de volta ao agente (que de alguma forma atualiza seu estado).

class Environment: def __init__(self, variants, payouts, n_trials, variance=False): self.variants = variants if variance: self.payouts = np.clip(payouts + np.random.normal(0, 0.04, size=len(variants)), 0, .2) else: self.payouts = payouts #self.payouts[5] = self.payouts[5] if i < n_trials/2 else 0.1 self.n_trials = n_trials self.total_reward = 0 self.n_k = len(variants) self.shape = (self.n_k, n_trials) def run(self, agent): """Run the simulation with the agent. agent must be a class with choose_k and update methods.""" for i in range(self.n_trials): # agent makes a choice x_chosen = agent.choose_k() # Environment returns reward reward = np.random.binomial(1, p=self.payouts[x_chosen]) # agent learns of reward agent.reward = reward # agent updates parameters based on the data agent.update() self.total_reward += reward agent.collect_data() return self.total_reward

Os pontos são distribuídos binomialmente com probabilidade p, dependendo do número da ação (assim como eles poderiam ser distribuídos continuamente, a essência não teria mudado). Também definirei a classe BaseSampler - é necessária apenas para armazenar logs e vários atributos.

 class BaseSampler: def __init__(self, env, n_samples=None, n_learning=None, e=0.05): self.env = env self.shape = (env.n_k, n_samples) self.variants = env.variants self.n_trials = env.n_trials self.payouts = env.payouts self.ad_i = np.zeros(env.n_trials) self.r_i = np.zeros(env.n_trials) self.thetas = np.zeros(self.n_trials) self.regret_i = np.zeros(env.n_trials) self.thetaregret = np.zeros(self.n_trials) self.a = np.ones(env.n_k) self.b = np.ones(env.n_k) self.theta = np.zeros(env.n_k) self.data = None self.reward = 0 self.total_reward = 0 self.k = 0 self.i = 0 self.n_samples = n_samples self.n_learning = n_learning self.e = e self.ep = np.random.uniform(0, 1, size=env.n_trials) self.exploit = (1 - e) def collect_data(self): self.data = pd.DataFrame(dict(ad=self.ad_i, reward=self.r_i, regret=self.regret_i))

Abaixo, definimos 10 opções e retorno para cada uma. A melhor opção é a opção 9, com um retorno de 0,11%.

 variants = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] payouts = [0.023, 0.03, 0.029, 0.001, 0.05, 0.06, 0.0234, 0.035, 0.01, 0.11]

Para ter algo para construir, também definimos a classe RandomSampler. Essa classe é necessária como modelo de linha de base. Ele simplesmente escolhe aleatoriamente uma opção em cada tentativa e não atualiza seus parâmetros.

 class RandomSampler(BaseSampler): def __init__(self, env): super().__init__(env) def choose_k(self): self.k = np.random.choice(self.variants) return self.k def update(self): # nothing to update #self.thetaregret[self.i] = self.thetaregret[self.i] #self.regret_i[self.i] = np.max(self.thetaregret) - self.theta[self.k] #self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.theta) - self.theta[self.k] self.a[self.k] += self.reward self.b[self.k] += 1 self.theta = self.a/self.b self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1

Outros modelos têm a seguinte estrutura. Todos têm métodos choose_k e de atualização. choose_k implementa o método pelo qual o agente seleciona uma opção. update atualiza os parâmetros do agente - esse método caracteriza como a capacidade do agente de escolher a opção muda (com o RandomSampler, essa capacidade não muda de forma alguma). Executamos o agente no ambiente usando o seguinte padrão.

 en0 = Environment(machines, payouts, n_trials=10000) rs = RandomSampler(env=en0) en0.run(agent=rs)

A essência do algoritmo épsilon-ganancioso é a seguinte.

Selecione k aleatoriamente para n tentativas.
Em cada tentativa, para cada opção, avalie o ganho.
Depois de todas as n tentativas:
Com probabilidade 1 - e escolha k com o maior ganho;
Com probabilidade e escolha K aleatoriamente.

Código Epsilon-ganancioso:

 class eGreedy(BaseSampler): def __init__(self, env, n_learning, e): super().__init__(env, n_learning, e) def choose_k(self): # e% of the time take a random draw from machines # random k for n learning trials, then the machine with highest theta self.k = np.random.choice(self.variants) if self.i < self.n_learning else np.argmax(self.theta) # with 1 - e probability take a random sample (explore) otherwise exploit self.k = np.random.choice(self.variants) if self.ep[self.i] > self.exploit else self.k return self.k # every 100 trials update the successes # update the count of successes for the chosen machine def update(self): # update the probability of payout for each machine self.a[self.k] += self.reward self.b[self.k] += 1 self.theta = self.a/self.b #self.total_reward += self.reward #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k] #self.thetaregret[self.i] = self.thetaregret[self.i] self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k] self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1

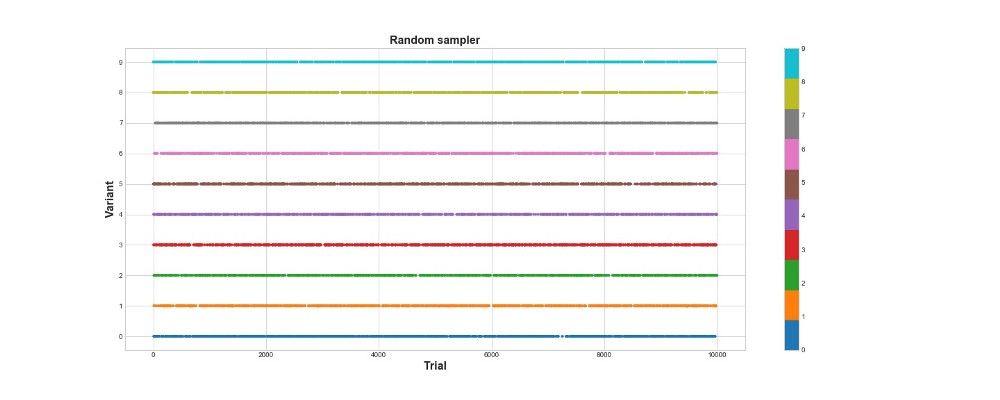
Abaixo no gráfico, você pode ver os resultados de uma amostra puramente aleatória, ou seja, não há modelo aqui. O gráfico mostra que escolha o algoritmo fez em cada tentativa, se houvesse 10 mil tentativas. O algoritmo apenas tenta, mas não aprende. No total, ele marcou 418 pontos.

Vamos ver como o algoritmo epsilon-ganancioso se comporta no mesmo ambiente. Execute o algoritmo para 10 mil tentativas com e = 0,1 e n_learning = 500 (o agente simplesmente tenta as primeiras 500 tentativas e, em seguida, tenta com probabilidade e = 0,1). Vamos avaliar o algoritmo de acordo com o número total de pontos que obtém no ambiente.

 en1 = Environment(machines, payouts, n_trials) eg = eGreedy(env=en1, n_learning=500, e=0.1) en1.run(agent=eg)

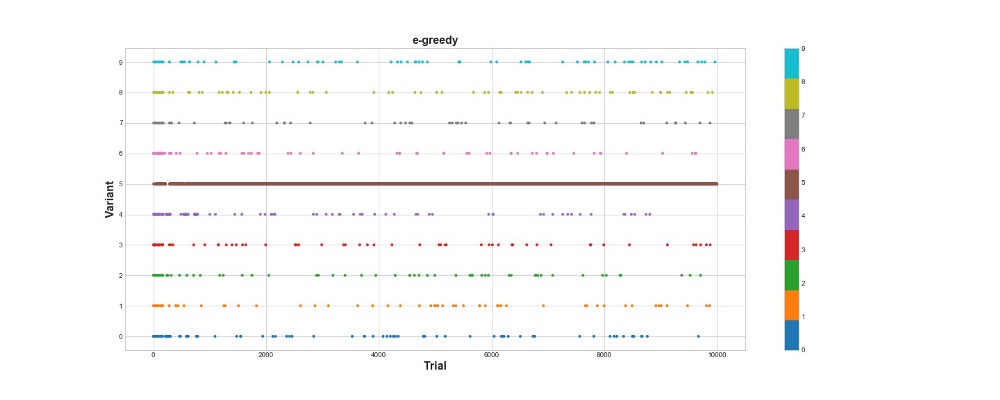
O algoritmo ganancioso Epsilon obteve 788 pontos, quase 2 vezes melhor que o algoritmo aleatório - super! O segundo gráfico explica esse algoritmo muito bem. Vemos que, para as primeiras 500 etapas, as ações são distribuídas aproximadamente uniformemente e K é escolhido aleatoriamente. No entanto, começa a explorar fortemente a opção 5 - essa é uma opção bastante forte, mas não é a melhor. Também vemos que o agente ainda seleciona aleatoriamente 10% do tempo.

Isso é muito legal - escrevemos apenas algumas linhas de código e agora já temos um algoritmo bastante poderoso que pode explorar o espaço de opções e tomar decisões próximas do ideal. Por outro lado, o algoritmo não encontrou a melhor opção. Sim, podemos aumentar o número de etapas para o aprendizado, mas dessa maneira gastaremos ainda mais tempo em uma pesquisa aleatória, piorando ainda mais o resultado final. Além disso, a aleatoriedade é costurada nesse processo por padrão - o melhor algoritmo pode não ser encontrado.

Mais tarde, rodarei cada um dos algoritmos várias vezes para que possamos compará-los um com o outro. Mas, por enquanto, vamos dar uma olhada na amostragem Thompson e testá-la no mesmo ambiente.

Amostragem Thompson

A amostragem de Thompson é fundamentalmente diferente do algoritmo epsilon-ganancioso em três pontos principais:

Não é ganancioso.
Faz tentativas de uma maneira mais sofisticada.
É bayesiano.

O ponto principal é o parágrafo 3, os parágrafos 1 e 2 seguem a partir dele.

A essência do algoritmo é esta:

Defina a distribuição beta inicial entre 0 e 1 para o retorno de cada opção.
Prove as opções desta distribuição, selecione o parâmetro Theta máximo.
Escolha a opção k que está associada ao maior teta.
Veja quantos pontos foram marcados, atualize os parâmetros de distribuição.

Leia mais sobre a distribuição beta aqui .
E sobre o seu uso em Python - aqui .

Código do algoritmo:

  class ThompsonSampler(BaseSampler): def __init__(self, env): super().__init__(env) def choose_k(self): # sample from posterior (this is the thompson sampling approach) # this leads to more exploration because machines with > uncertainty can then be selected as the machine self.theta = np.random.beta(self.a, self.b) # select machine with highest posterior p of payout self.k = self.variants[np.argmax(self.theta)] #self.k = np.argmax(self.a/(self.a + self.b)) return self.k def update(self): #update dist (a, b) = (a, b) + (r, 1 - r) self.a[self.k] += self.reward self.b[self.k] += 1 - self.reward # ie only increment b when it's a swing and a miss. 1 - 0 = 1, 1 - 1 = 0 #self.thetaregret[self.i] = self.thetaregret[self.i] #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k] self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k] self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1

A notação formal do algoritmo se parece com isso.

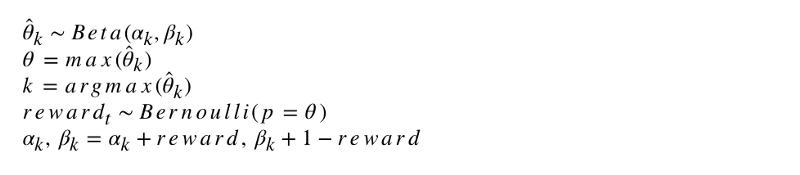
Vamos programar esse algoritmo. Como outros agentes, o ThompsonSampler herda do BaseSampler e define seus próprios métodos choose_k e update. Agora lance nosso novo agente.

  en2 = Environment(machines, payouts, n_trials) tsa = ThompsonSampler(env=en2) en2.run(agent=tsa)

Como você pode ver, ele marcou mais do que o algoritmo epsilon-ganancioso. Ótimo! Vejamos o gráfico da seleção de tentativas. Duas coisas interessantes são visíveis nele. Primeiro, o agente descobriu corretamente a melhor opção (opção 9) e a usou ao máximo. Em segundo lugar, o agente usou outras opções, mas de uma maneira mais complicada - após cerca de 1000 tentativas, o agente, além da opção principal, usou principalmente as opções mais poderosas entre as outras. Em outras palavras, ele não escolheu aleatoriamente, mas com mais competência.

Por que isso funciona? É simples - a incerteza na distribuição posterior dos benefícios esperados para cada opção significa que cada opção é selecionada com uma probabilidade aproximadamente proporcional à sua forma, determinada pelos parâmetros alfa e beta. Em outras palavras, em cada tentativa, a amostragem Thompson aciona a opção de acordo com a probabilidade posterior de que ele tenha o benefício máximo. Grosso modo, tendo pela distribuição informações sobre incertezas, o agente decide quando examinar o ambiente e quando usar as informações. Por exemplo, uma opção fraca com alta incerteza posterior pode pagar mais por essa tentativa. Mas para a maioria das tentativas, quanto mais forte sua distribuição posterior, maior sua média e menor seu desvio padrão e, portanto, maior a chance de escolhê-la.

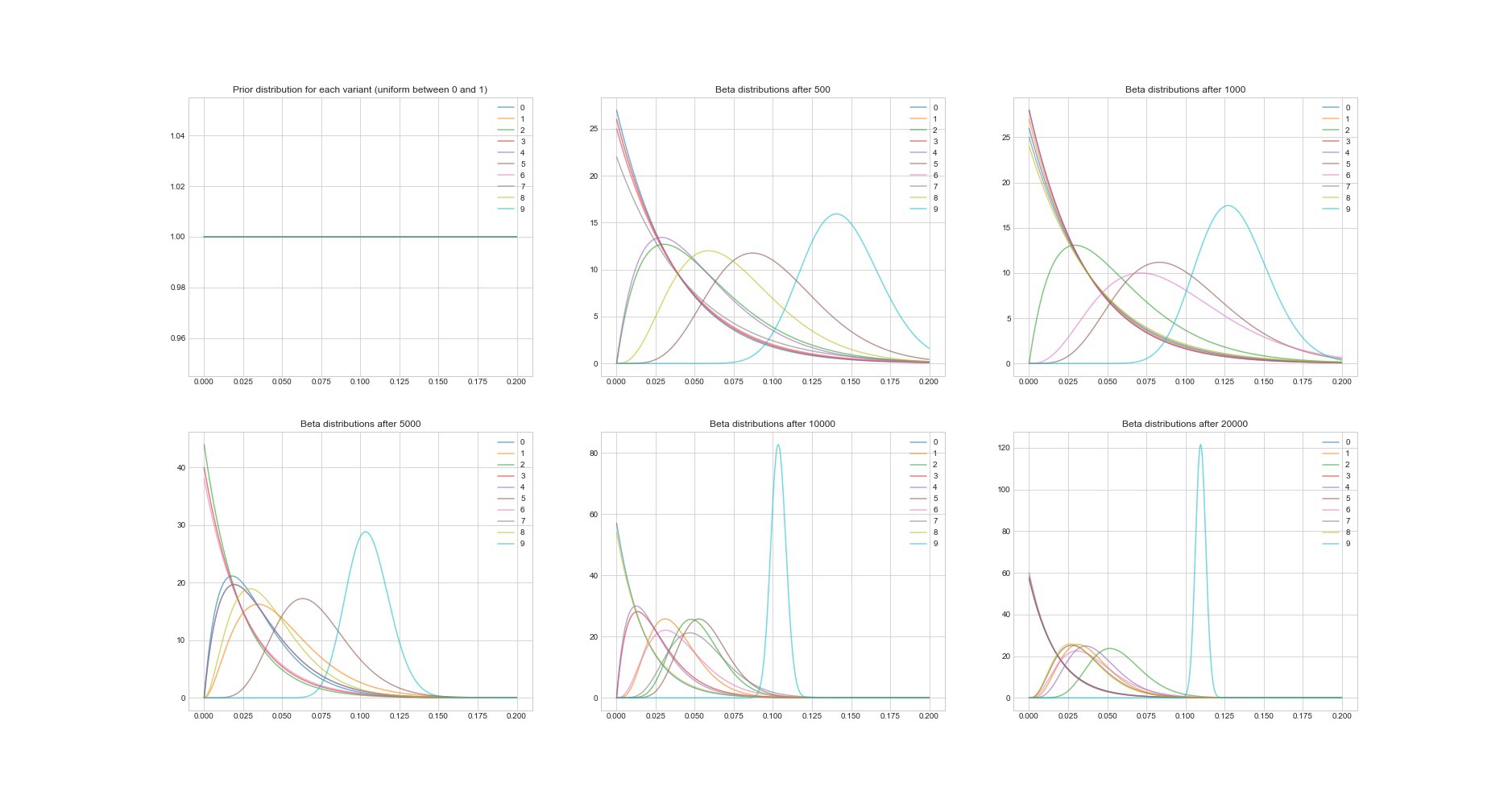
Outra propriedade notável do algoritmo de Thompson: como é bayesiano, podemos estimar a incerteza na estimativa de retorno de cada opção usando seus parâmetros. O gráfico abaixo mostra as distribuições posteriores em 6 pontos diferentes e em 20.000 tentativas. Você vê como as distribuições gradualmente começam a convergir para a opção com o melhor retorno.

Agora compare todos os 3 agentes em 100 simulações. 1 simulação é um lançamento do agente em 10.000 tentativas.

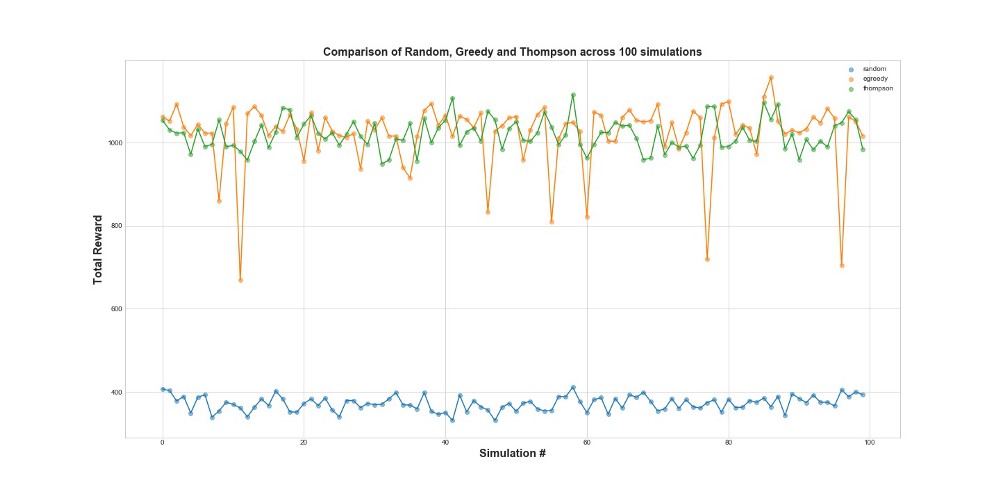
Como você pode ver no gráfico, a estratégia epsilon-greedy e a amostragem Thompson funcionam muito melhor do que a amostragem aleatória. Você pode se surpreender com o fato de a estratégia epsilon-gananciosa e a amostragem Thompson serem realmente comparáveis em termos de desempenho. A estratégia gananciosa de Epsilon pode ser muito eficaz, mas é mais arriscada, porque pode ficar presa em uma opção abaixo do ideal - isso pode ser visto nas falhas no gráfico. Mas a amostragem Thompson não pode, porque faz a escolha no espaço de opções de uma maneira mais complexa.

Arrependimento

Outra maneira de avaliar quão bem o algoritmo funciona é avaliar o arrependimento. Grosso modo, quanto menor, em relação às ações já tomadas, melhor. Abaixo está um gráfico do total arrependimento e arrependimento pelo erro. Mais uma vez - quanto menos arrependimento, melhor.

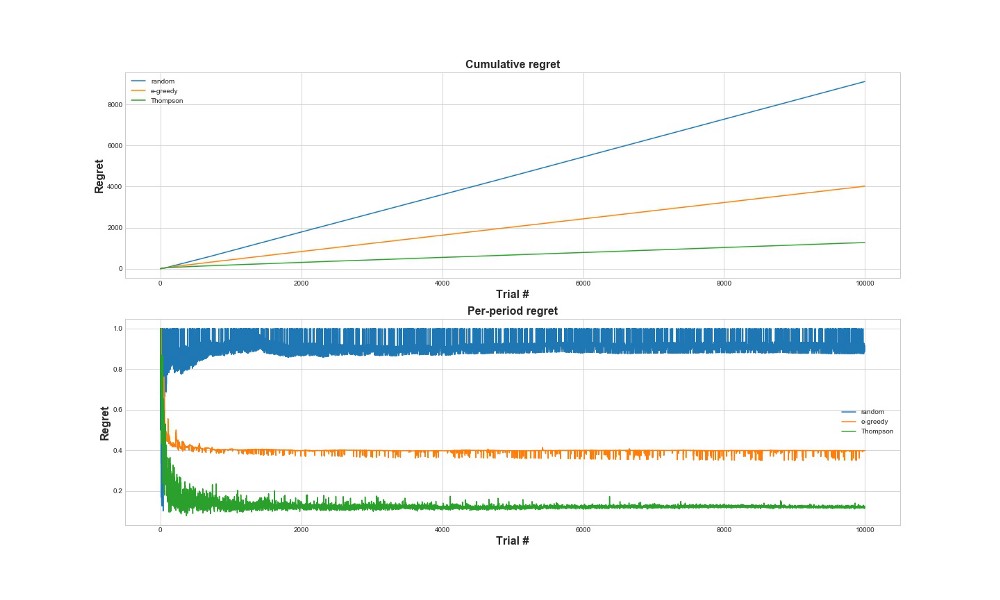
No gráfico superior, vemos o arrependimento total e, no arrependimento inferior, a tentativa. Como pode ser visto nos gráficos, a amostragem Thompson converge para um arrependimento mínimo muito mais rápido do que a estratégia epsilon-gananciosa. E converge para um nível mais baixo. Com a amostragem Thompson, o agente se arrepende menos porque pode detectar melhor a melhor opção e tentar as opções mais promissoras melhor - portanto, a amostragem Thompson é particularmente adequada para casos de uso mais avançados, como modelos estatísticos ou redes neurais para escolher k.

Conclusões

Este é um post técnico bastante longo. Para resumir, podemos usar métodos de amostragem bastante sofisticados se tivermos muitas opções que queremos testar em tempo real. Uma das características muito boas da amostragem Thompson é que ela equilibra o uso e a exploração de uma maneira bastante complicada. Ou seja, podemos deixá-lo otimizar a distribuição das opções da solução em tempo real. Esses são algoritmos interessantes e devem ser mais úteis para os negócios do que os testes A / B.

Importante! A amostragem Thompson não significa que você não precisa fazer testes A / B. Normalmente, eles primeiro encontram as melhores opções com a ajuda dele e depois fazem testes A / B já.

O problema dos bandidos com várias armas - compare a estratégia Epsilon-Greedy e a amostragem Thompson