A implementação de algoritmos em Python usando cálculos simbólicos é muito conveniente para resolver problemas de modelagem matemática de objetos definidos por equações diferenciais. Para resolver essas equações, as transformadas de Laplace são amplamente utilizadas, o que, em termos simplificados, possibilita reduzir o problema à resolução de equações algébricas simples.
Nesta publicação, proponho considerar as funções das transformadas diretas e inversas de Laplace da biblioteca SymPy, que permitem usar o método Laplace para resolver equações diferenciais e sistemas usando Python.
O método de Laplace em si e suas vantagens na resolução de equações e sistemas diferenciais lineares são amplamente abordados na literatura, por exemplo, na publicação popular [1]. No livro, o método Laplace é apresentado para implementação em pacotes de software licenciado Mathematica, Maple e MATLAB (que implica a compra deste software por uma instituição educacional) usando exemplos selecionados do autor.
Hoje, tentaremos considerar não um exemplo separado de solução de um problema de aprendizado usando Python, mas um método geral para resolver equações diferenciais lineares e sistemas usando as funções de transformadas diretas e inversas de Laplace. Ao mesmo tempo, salvaremos um momento de aprendizado: o lado esquerdo da equação diferencial linear com condições de Cauchy será formado pelo próprio aluno e a parte rotineira da tarefa, que consiste na transformação direta de Laplace do lado direito da equação, será executada usando a função
laplace_transform () .
A história da autoria do Laplace transforma
As transformadas de Laplace (imagens de Laplace) têm uma história interessante. Pela primeira vez, a integral na definição da transformada de Laplace apareceu em uma das obras de L. Euler. No entanto, é geralmente aceito na matemática chamar uma metodologia ou teorema o nome do matemático que a descobriu depois de Euler. Caso contrário, haveria várias centenas de teoremas de Euler diferentes.
Nesse caso, o próximo, depois de Euler, foi o matemático francês Pierre Simon de Laplace (Pierre Simon de Laplace (1749-1827)). Foi ele quem usou tais integrais em seu trabalho sobre teoria das probabilidades. O próprio Laplace não aplicou os chamados "métodos operacionais" para encontrar soluções de equações diferenciais baseadas nas transformadas de Laplace (imagens de Laplace). Esses métodos foram realmente descobertos e popularizados por engenheiros práticos, especialmente o engenheiro elétrico inglês Oliver Heaviside (1850-1925). Muito antes de a validade desses métodos ser rigorosamente comprovada, o cálculo operacional foi utilizado com sucesso e amplamente, embora sua legitimidade tenha sido questionada em grande parte, mesmo no início do século XX, e houve um debate muito acirrado sobre esse assunto.
Funções da transformada direta e inversa de Laplace
- Função de transformação direta de Laplace:
sympy.integrals.transforms. laplace_transform (t, s, ** dicas).
A função laplace_transform () executa as transformadas de Laplace da função f (t) da variável real na função F (s) da variável complexa, de modo que:
F ( s ) = i n t ∞ 0 f ( t ) e - s t d t .
Essa função retorna (F, a, cond) , onde F (s) é a transformada de Laplace da função f (t) , a <Re (s) é o semiplano em que F (s) é definido e cond são condições auxiliares para a convergência da integral.
Se a integral não puder ser calculada em formato fechado, essa função retornará um objeto LaplaceTransform não computado .
Se você definir a opção noconds = True , a função retornará apenas F (s) . - Função de transformação inversa de Laplace:
sympy.integrals.transforms. inverse_laplace_transform (F, s, t, plane = None, ** dicas).
A função inverse_laplace_transform () executa a transformação inversa de Laplace da função da variável complexa F (s) na função f (t) da variável real, de modo que:
f ( t ) = f r um c 1 2 p i i i n t c + ∞ c d o t i c - ∞ c d o t i e s t F ( s ) d s .
Se a integral não puder ser calculada de forma fechada, essa função retornará o InverseLaplaceTransform não chamado do objeto.
A transformada inversa de Laplace no exemplo da determinação das características de transição dos reguladores
A função de transferência do controlador PID tem a forma [2]:
W(s)=(1+ fracKd cdotTd cdots1+Td cdots) cdotKp cdot(1+ frac1Ti cdots) c d o t f r um c 1 s .
Escreveremos um programa para obter equações para as características transitórias dos controladores PID e PI para a função de transferência reduzida e derivaremos adicionalmente o tempo gasto na transformação visual inversa de Laplace.
Temos:Tempo de transformação reverso do Laplace Visual: 2.68 s
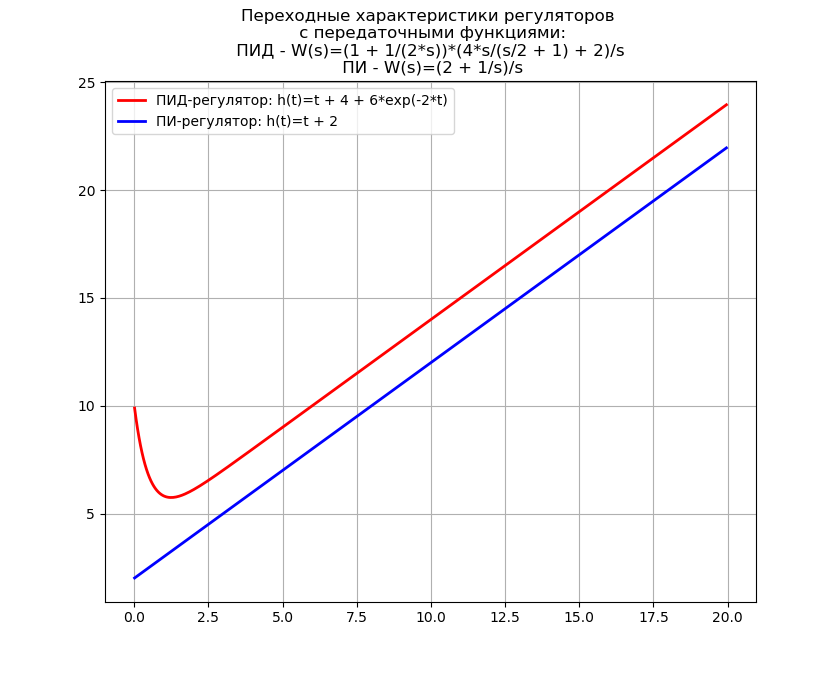
A transformação inversa de Laplace é frequentemente usada na síntese de armas de autopropulsão, onde o Python pode substituir "monstros" caros de software como o MathCAD, portanto, o uso acima da transformação inversa é de importância prática.
Transformação de Laplace a partir de derivadas de ordens mais altas para resolver o problema de Cauchy
Nossa discussão continuará com a aplicação das transformadas de Laplace (imagens de Laplace) na busca de soluções de uma equação diferencial linear com coeficientes constantes da forma:
a c d o t x ″ ( t ) + b c d o t x ′ ( t ) + c c d o t x ( t ) = f ( t ) . ( 1 )
Se
aeb são constantes, então
L \ left \ {a \ cdot f (t) + b \ cdot q (t) \ right \} = a \ cdot L \ left \ {f (t) \ right \} + b \ cdot L \ left \ {q (t) \ right \} (2)
L \ left \ {a \ cdot f (t) + b \ cdot q (t) \ right \} = a \ cdot L \ left \ {f (t) \ right \} + b \ cdot L \ left \ {q (t) \ right \} (2)
para todos
s de modo que existem as transformadas de Laplace (imagem de Laplace) das funções
f (t) e
q (t) .
Vamos verificar a linearidade das transformadas diretas e inversas de Laplace usando as funções anteriormente consideradas
laplace_transform () e
inverse_laplace_transform () . Para isso, tomamos
f (t) = sin (3t) ,
q (t) = cos (7t) ,
a = 5 ,
b = 7 como exemplo e usamos o programa a seguir.
Texto do programa from sympy import* var('sa b') var('t', positive=True) a = 5 f = sin(3*t) b = 7 q = cos(7*t)
Temos:(7 * s ** 3 + 15 * s ** 2 + 63 * s + 735) / ((s ** 2 + 9) * (s ** 2 + 49))
(7 * s ** 3 + 15 * s ** 2 + 63 * s + 735) / ((s ** 2 + 9) * (s ** 2 + 49))
Verdadeiro
5 * pecado (3 * t) + 7 * cos (7 * t)
5 * pecado (3 * t) + 7 * cos (7 * t)
O código acima também demonstra a exclusividade da transformação inversa de Laplace.
Assumindo que
q(t)=f′(t) satisfaz as condições do primeiro teorema, a partir deste teorema, segue-se que:
L \ esquerda \ {f '' (t) \ direita \} = L \ esquerda \ {q '(t) \ direita \} = sL \ esquerda \ {q (t) \ direita \} - q (0) = sL \ esquerda \ {f '(t) \ direita \} - f' (0) = s \ esquerda [sL \ esquerda \ {f (t) -f (0) \ direita \} \ direita],
L \ esquerda \ {f '' (t) \ direita \} = L \ esquerda \ {q '(t) \ direita \} = sL \ esquerda \ {q (t) \ direita \} - q (0) = sL \ esquerda \ {f '(t) \ direita \} - f' (0) = s \ esquerda [sL \ esquerda \ {f (t) -f (0) \ direita \} \ direita],
e assim
L \ left \ {f '' (t) \ right \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f '(0).
L \ left \ {f '' (t) \ right \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f '(0).
Repetir esse cálculo fornece
L \ left \ {f '' '(t) \ right \} = sL \ left \ {f' '(t) \ right \} - f' '(0) = s ^ {3} F (s) -s ^ {2} f (0) -sf '(0) -f' '(0).
L \ left \ {f '' '(t) \ right \} = sL \ left \ {f' '(t) \ right \} - f' '(0) = s ^ {3} F (s) -s ^ {2} f (0) -sf '(0) -f' '(0).
Após um número finito de tais etapas, obtemos a seguinte generalização do primeiro teorema:
L \ esquerda \ {f ^ {(n)} (t) \ direita \} = s ^ {n} L \ esquerda \ {f (t) \ direita \} - s ^ {n-1} f (0 ) -s ^ {n-2} f '(0) - \ cdot \ cdot \ cdot -f ^ {(n-1)} (0) =
L \ esquerda \ {f ^ {(n)} (t) \ direita \} = s ^ {n} L \ esquerda \ {f (t) \ direita \} - s ^ {n-1} f (0 ) -s ^ {n-2} f '(0) - \ cdot \ cdot \ cdot -f ^ {(n-1)} (0) =
=snF(s)−sn−1f(0)− cdot cdot cdot−sf(n−2)(0)−f(n−1)(0).(3)
Aplicando a relação (3) contendo os derivados transformados de Laplace da função desejada com as condições iniciais da equação (1), podemos obter sua solução de acordo com o método especialmente desenvolvido em nosso departamento com o suporte ativo de
Scorobey para a biblioteca SymPy.
Um método para resolver equações diferenciais lineares e sistemas de equações com base em transformadas de Laplace usando a biblioteca SymPy
Para demonstrar o método, usamos uma equação diferencial simples que descreve o movimento de um sistema que consiste em um ponto material de uma dada massa, montada em uma mola na qual uma força externa é aplicada. A equação diferencial e as condições iniciais para esse sistema têm a forma:
x″+4x= sin(3t);x(0)=1,2;x′(0)=1,(4)
onde
x(0) - posição inicial reduzida da massa,
x′(0) - velocidade inicial de massa reduzida.
Um modelo físico simplificado definido pela equação (4) com condições iniciais diferentes de zero [1]:
Um sistema que consiste em um ponto material de uma determinada massa fixada em uma mola satisfaz o problema de Cauchy (um problema com as condições iniciais). O ponto material de uma dada massa está inicialmente em repouso na sua posição de equilíbrio.
Para resolver esta e outras equações diferenciais lineares pelo método de transformação de Laplace, é conveniente usar o seguinte sistema obtido das relações (3):
L \ left \ {f ^ {IV} (t) \ right \} = s ^ {4} \ cdot F (s) -s ^ {3} \ cdot f (0) -s ^ {2} \ cdot f ^ {I} (0) -s \ cdot f ^ {II} (0) -f ^ {III} (0),L \ left \ {f ^ {III} (t) \ right \} = s ^ {3} \ cdot f (s) -s ^ {2} \ cdot f (0) -s \ cdot f ^ {I } (0) -f ^ {II} (0),L \ left \ {f ^ {II} (t) \ right \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f ^ {I} (0),L \ esquerda \ {f ^ {I} (t) \ direita \} = s \ cdot F (s) -f (0), L \ esquerda \ {f (t) \ direita \} = F (s) .L \ esquerda \ {f (t) \ direita \} = F (s). (5)A sequência de soluções usando o SymPy é a seguinte:
- carregue os módulos necessários e defina explicitamente variáveis simbólicas:
from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function)
- especifique a versão da biblioteca sympy para levar em conta seus recursos. Para fazer isso, digite as seguintes linhas:
import SymPy print (' sympy – %' % (sympy._version_))
- de acordo com o significado físico do problema, a variável tempo é determinada para uma região que inclui números zero e positivos. Definimos as condições iniciais e a função no lado direito da equação (4) com sua subsequente transformação de Laplace. Para condições iniciais, você deve usar a função Rational, pois o uso do arredondamento decimal resulta em um erro.
- usando (5), reescrevemos as derivadas convertidas de Laplace incluídas no lado esquerdo da equação (4), formando o lado esquerdo dessa equação e comparando o resultado com o lado direito:
d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = d2 + 4*d0 de = Eq(d, Lg)
- resolvemos a equação algébrica obtida para a transformação X (s) e executamos a transformada inversa de Laplace:
rez = solve(de, X(s))[0] soln = inverse_laplace_transform(rez, s, t)
- Transferimos do trabalho na biblioteca SymPy para a biblioteca NumPy:
f = lambdify(t, soln, 'numpy')
- traçamos o método Python usual:
x = np.linspace(0, 6*np.pi, 100) plt.title(', \n :\n (t)=%s' % soln) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()
Texto completo do programa: from sympy import * import numpy as np import matplotlib.pyplot as plt import sympy var('s') var('t', positive=True) var('X', cls=Function) print (" sympy – %s" % (sympy.__version__))
Temos:Versão da biblioteca Sympy - 1.3
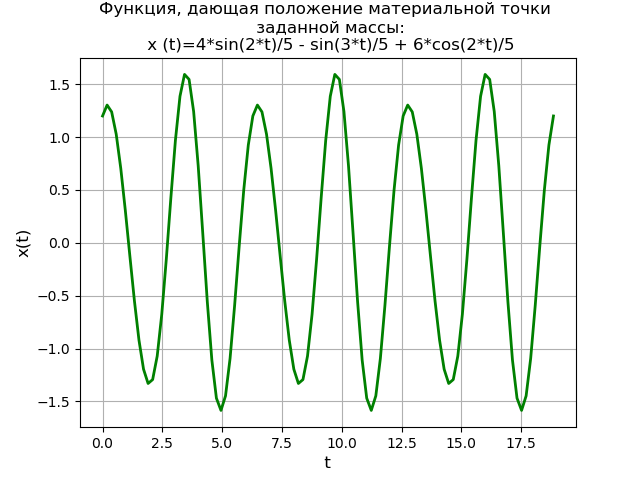
É obtido um gráfico da função periódica que indica a posição do ponto do material de uma determinada massa. O método de transformação Laplace usando a biblioteca SymPy fornece uma solução não apenas sem a necessidade de encontrar uma solução geral para uma equação homogênea e uma solução específica para a equação diferencial heterogênea inicial, mas também sem a necessidade de usar o método de fração elementar e as tabelas Laplace.
Ao mesmo tempo, o valor educacional do método da solução é preservado devido à necessidade de usar o sistema (5) e ir ao NumPy para estudar soluções usando métodos mais produtivos.
Para demonstrar ainda mais o método, resolvemos o sistema de equações diferenciais:
begincases2x″+6x−2=0,y″−2x+2y=40 cdot sin(3t), endcases(6)com condições iniciais
x(0)=y(0)=y′(0)=0.Um modelo físico simplificado definido pelo sistema de equações (6) sob zero condições iniciais:

Assim, a força
f (t) é subitamente aplicada ao segundo ponto material de uma dada massa no tempo
t = 0 , quando o sistema está em repouso na sua posição de equilíbrio.
A solução do sistema de equações é idêntica à solução anteriormente considerada da equação diferencial (4), portanto, dou o texto do programa sem explicação.
Texto do programa from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t ', positive=True) var('X Y', cls=Function) x0 = 0 x01 = 0 y0 = 0 y01 = 0 g = 40 * sin(3*t) Lg = laplace_transform(g, t, s, noconds=True) de1 = Eq(2*(s**2*X(s) - s*x0 - x01) + 6*X(s) - 2*Y(s)) de2 = Eq(s**2*Y(s) - s*y0 - y01 - 2*X(s) + 2*Y(s) - Lg) rez = solve([de1, de2], X(s), Y(s)) rezX = expand(rez[X(s)]) solnX = inverse_laplace_transform(rezX, s, t) rezY = expand(rez[Y(s)]) solnY = inverse_laplace_transform(rezY, s, t) f = lambdify(t, solnX, "numpy") F = lambdify(t, solnY, "numpy") x = np.linspace(0, 4*np.pi, 100) plt.title(' :\nx(t)=%s\ny(t)=%s' % (solnX, solnY)) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t), y(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2, label='x(t)') plt.plot(x, F(x), 'b', linewidth=2, label='y(t)') plt.legend(loc='best') plt.show()
Temos: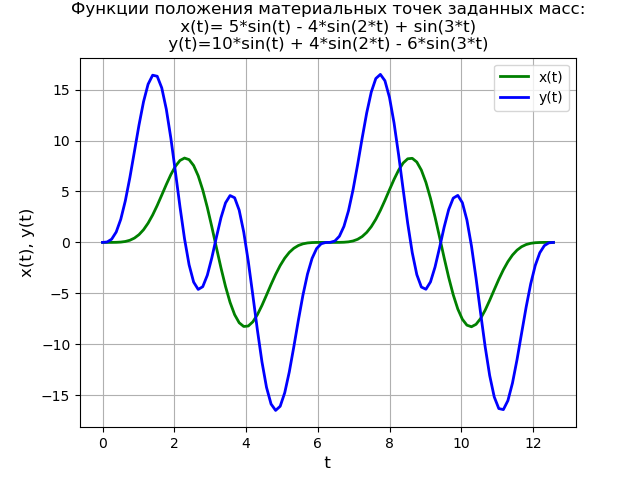
Para condições iniciais diferentes de zero, o texto do programa e o gráfico da função assumem a forma:
Texto do programa from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X Y', cls=Function) x0 = 0 x01 = -1 y0 = 0 y01 = -1 g = 40 * sin(t) Lg = laplace_transform(g, t, s, noconds=True) de1 = Eq(2*(s**2*X(s) - s*x0 - x01) + 6*X(s) - 2*Y(s)) de2 = Eq(s**2*Y(s) - s*y0 - y01 - 2*X(s) + 2*Y(s) - Lg) rez = solve([de1, de2], X(s), Y(s)) rezX = expand(rez[X(s)]) solnX = (inverse_laplace_transform(rezX, s, t)).evalf().n(3) rezY = expand(rez[Y(s)]) solnY = (inverse_laplace_transform(rezY, s, t)).evalf().n(3) f = lambdify(t, solnX, "numpy") F = lambdify(t, solnY, "numpy") x = np.linspace(0, 4*np.pi, 100) plt.title(' :\nx(t)= %s \ny(t)=%s' % (solnX, solnY)) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t), y(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2, label='x(t)') plt.plot(x, F(x), 'b', linewidth=2, label='y(t)') plt.legend(loc='best') plt.show()
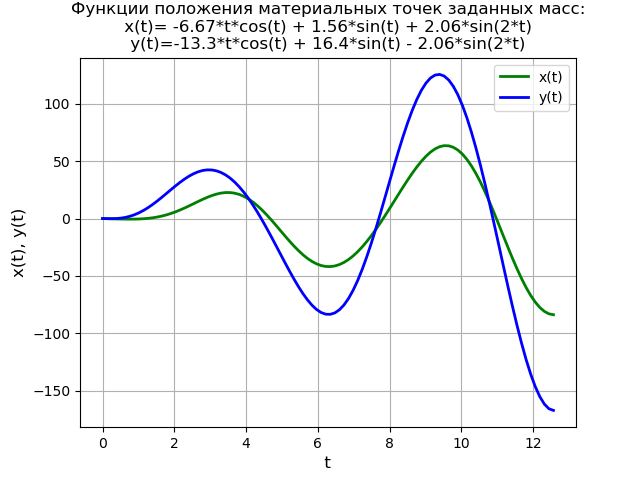
Considere a solução de uma equação diferencial linear de quarta ordem com zero condições iniciais:
x(4)+2 cdotx″+x=4 cdott cdotet;x(0)=x′(0)=x″(0)=x(3)(0)=0.Texto do programa: from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function)
Cronograma de decisão:
Resolvemos a equação diferencial linear de quarta ordem:
x(4)+13x″+36x=0;com condições iniciais
x(0)=x″(0)=0 ,
x′(0)=2 ,
x(3)(0)=−13 .
Texto do programa: from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function)
Cronograma de decisão: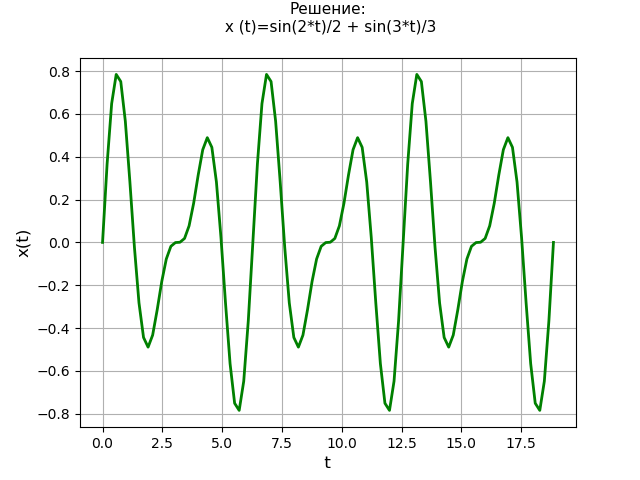
Funções para resolver ODE
Para sistemas ODE e ODE com uma solução analítica, a função
dsolve () é usada:
sympy.solvers.ode.
dsolve (eq, func = Nenhum, dica = 'padrão', simplificar = Verdadeiro, ics = Nenhum, xi = Nenhum, eta = Nenhum, x0 = 0, n = 6, ** kwargs)
Vamos comparar o desempenho da função dsolve () com o método Laplace. Por exemplo, considere a seguinte equação diferencial de quarto grau com zero condições iniciais:
x(IV)(t)=3 cdotx‴(t)−x(t)=4 cdott cdot exp(t);x(0)=x′(0)=x″(0)=x‴(0)=0.Um programa usando a função dsolve (): from sympy import * import time import numpy as np import matplotlib.pyplot as plt start = time.time() var('t C1 C2 C3 C4') u = Function("u")(t)
Temos:Tempo da equação usando a função dsolve (): 1.437 s
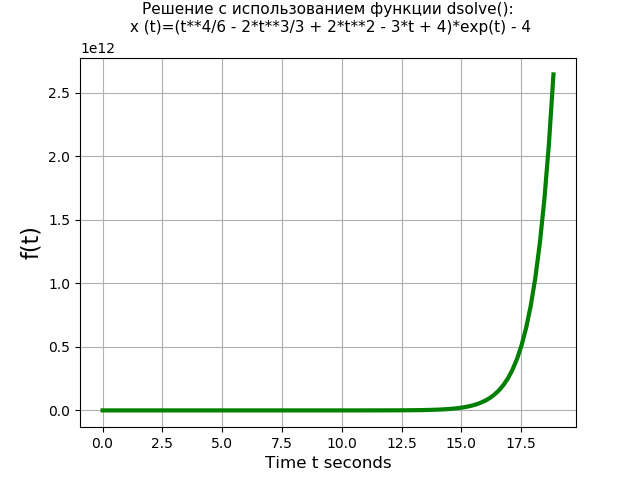
Programa usando transformadas de Laplace: from sympy import * import time import numpy as np import matplotlib.pyplot as plt start = time.time() var('s') var('t', positive=True) var('X', cls=Function)
Temos:Tempo da equação usando a transformada de Laplace: 3,274 s

Portanto, a função dsolve () (1.437 s) resolve a equação de quarta ordem mais rapidamente do que a resolução pelo método de transformação de Laplace (3.274 s) mais de duas vezes. No entanto, deve-se notar que a função dsolve () não resolve o sistema de equações diferenciais de segunda ordem, por exemplo, ao resolver o sistema (6) usando a função dsolve (), ocorre um erro:
from sympy import* t = symbols('t') x, y = symbols('x, y', Function=True) eq = (Eq(Derivative(x(t), t, 2), -3*x(t) + y(t)), Eq(Derivative(y(t), t, 2), 2*x(t) - 2*y(t) + 40*sin(3*t))) rez = dsolve(eq) print (list(rez))
Temos:raiseNotImplementedError
NotImplementedError
Este erro significa que a solução do sistema de equações diferenciais usando a função
dsolve () não pode ser representada simbolicamente. Considerando que, com a ajuda das transformadas de Laplace, obtivemos uma representação simbólica da solução, e isso prova a eficácia do método proposto.
NotaPara encontrar o método necessário para resolver equações diferenciais usando a função
dsolve () , você precisa usar
classify_ode (eq, f (x)) , por exemplo:
from sympy import * from IPython.display import * import matplotlib.pyplot as plt init_printing(use_latex=True) x = Symbol('x') f = Function('f') eq = Eq(f(x).diff(x, x) + f(x), 0) print (dsolve(eq, f(x))) print (classify_ode(eq, f(x))) eq = sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x) print (classify_ode(eq, f(x))) rez = dsolve(eq, hint='almost_linear_Integral') print (rez)
Temos:Eq (f (x), C1 * sin (x) + C2 * cos (x))
('nth_linear_constant_coeff_homogeneous', '2nd_power_series_ordinary')
('separável', '1º_exato', 'quase_linear', '1º_poder_série', 'ment_grupo', 'separável_Integral', '1º_exato_Integral', 'almost_linear_Integral')
[Eq (f (x), -acos ((C1 + Integral (0, x)) * exp (-Integral (-tan (x), x))) + 2 * pi), Eq (f (x), acos ((C1 + Integral (0, x)) * exp (-Integral (-tan (x), x)))]]
Assim, para a equação
eq = Eq (f (x) .diff (x, x) + f (x), 0) , qualquer método da primeira lista funciona:
nth_linear_constant_coeff_homogeneous,
2nd_power_series_ordinary
Para a equação
eq = sin (x) * cos (f (x)) + cos (x) * sin (f (x)) * f (x) .diff (x) , qualquer método da segunda lista funciona:
separável, 1st_exact, quase_linear,
1st_power_series, lie_group, separable_Integral,
1st_exact_Integral, quase_linear_Integral
Para usar o método selecionado, a entrada da função dsolve () assumirá o formato, por exemplo:
rez = dsolve(eq, hint='almost_linear_Integral')
Conclusão:
Este artigo teve como objetivo mostrar como usar as ferramentas das bibliotecas SciPy e NumPy no exemplo de solução de sistemas ODE lineares usando o método do operador. Assim, foram considerados os métodos de solução simbólica de equações diferenciais lineares e sistemas de equações pelo método de Laplace. A análise do desempenho desse método e dos métodos implementados na função dsolve () é realizada.
Referências:- Equações diferenciais e problemas de valor-limite: modelagem e cálculo usando o Mathematica, Maple e MATLAB. 3ª edição.: Per. do inglês - M .: LLC “I.D. Williams, 2008. - 1104 p .: III. Paral. tit. Inglês
- Usando a conversão inversa de Laplace para analisar os links dinâmicos dos sistemas de controle