Aprenda o OpenGL. Lição 6.1. PBR ou renderização fisicamente correta. Teoria

Renderização fisicamente correta

PBR, ou renderização com base física, é um conjunto de técnicas de visualização baseadas em uma teoria que concorda muito bem com a teoria real da propagação da luz. Como o objetivo da PBR é uma simulação de luz fisicamente confiável, ela parece muito mais realista em comparação com os modelos de iluminação Phong e Blinn-Fong que usamos anteriormente. Ele não apenas parece melhor, mas também oferece uma boa aproximação à física real, o que nos permite (e artistas em particular) criar materiais com base nas propriedades físicas das superfícies sem recorrer a truques baratos para tornar a iluminação mais realista. A principal vantagem dessa abordagem é que os materiais que criamos parecerão planejados, independentemente das condições de iluminação, o que não pode ser dito sobre outras abordagens, não a PBR.

No entanto, a PBR ainda é uma aproximação da realidade (com base nas leis da física), e é por isso que é chamada renderização fisicamente correta, não renderização física. Para que o modelo de iluminação possa ser considerado fisicamente correto, ele deve atender a 3 condições (não se preocupe, entraremos em contato com eles em breve):

• Baseado em um modelo de micro facetas reflexivas
• Obedecer à lei de conservação de energia
• Use a função de distribuição de refletância de feixe duplo (BRDF)

Nesta série de tutoriais, focaremos a abordagem PBR, originalmente desenvolvida na Disney e adaptada para visualização em tempo real pela Epic Games. Sua abordagem, baseada em um fluxo de trabalho metal-dielétrico ( fluxo de trabalho metálico, não encontrou uma tradução melhor - aprox. Ed. ), É bem documentada, amplamente aceita em muitos motores populares e tem uma aparência incrível. No final desta seção, obtemos algo semelhante a este:

Lembre-se de que os artigos desta seção são bastante avançados, portanto, é recomendável que você tenha um bom entendimento do OpenGL e da iluminação de sombreador. Aqui estão alguns dos conhecimentos necessários para estudar esta seção: buffer de quadros , mapas cúbicos , correção de gama , HDR e mapas normais . Também aprofundaremos um pouco mais a matemática, mas prometo fazer todo o possível para explicar tudo da maneira mais clara possível.

Modelo de micro facetas reflexivas

Todas as técnicas de PBR são baseadas na teoria das micro faces. Essa teoria diz que cada superfície com alta ampliação pode ser representada como um conjunto de espelhos microscópicos chamados micro faces . Devido à rugosidade da superfície, esses micro-espelhos podem ser orientados em diferentes direções:

Quanto mais rugosa a superfície, mais aleatoriamente são as suas micro-faces. O resultado desse arranjo desses pequenos espelhos é (principalmente quando se trata de reflexos e reflexos especulares) que os raios de luz incidentes são espalhados em diferentes direções em superfícies ásperas, o que leva a um reflexo especular mais amplo. E vice-versa: em superfícies lisas, é mais provável que os raios incidentes sejam refletidos em uma direção, o que dará um brilho menor e mais nítido:

No nível microscópico, não existem superfícies absolutamente lisas, mas, como as micro-faces são pequenas o suficiente e não podemos distinguir entre elas no espaço de pixels, aproximamos estatisticamente a rugosidade da superfície, introduzindo um coeficiente de rugosidade . Usando esse coeficiente, podemos calcular a fração de micro-faces orientadas na direção de um determinado vetor $$$h$ . Esse vetor $$$h$ nada além de um vetor mediano no meio, entre a direção da luz incidente $$$l$ e direção do observador $$$v$ . Falamos sobre isso anteriormente em uma lição sobre iluminação avançada , onde a definimos como a razão da soma dos vetores $$$l$ e $$$v$ para o comprimento do vetor resultante:

$$

$$h = \ frac {l + v} {|| l + v ||}$$

Quanto mais micro-faces orientadas na direção do vetor mediano, mais nítido e brilhante será o destaque especular. Devido ao coeficiente de rugosidade, que fica entre 0 e 1, podemos aproximar estatisticamente a orientação das micro faces:

Como você pode ver, um valor mais alto do coeficiente de rugosidade fornece um ponto de reflexo de espelho de tamanho maior, em comparação com um ponto pequeno e nítido em superfícies lisas.

Conservação de energia.

O uso da aproximação levando em consideração as micro faces já traz uma certa forma de conservação de energia: a energia da luz refletida nunca excederá a energia da luz incidente (se a superfície não brilhar sozinha). Observando a imagem acima, vemos que, com um aumento na rugosidade da superfície, o ponto da luz refletida aumenta, mas, ao mesmo tempo, seu brilho diminui. Se a intensidade da luz refletida for a mesma para todos os pixels, independentemente do tamanho do ponto, superfícies mais ásperas emitirão muito mais energia, o que violaria a lei de conservação de energia. Portanto, reflexões especulares são mais brilhantes em superfícies lisas e escuras em superfícies ásperas.

Para que a energia seja conservada, precisamos fazer uma separação clara entre os componentes difuso e espelho. Nesse momento, quando um raio de luz atinge a superfície, ele é dividido em componentes refletidos e refratados . O componente refletido é a luz refletida diretamente e não penetra na superfície; nós o conhecemos como um componente espelho da luz. O componente refratado é a luz que penetra na superfície e é absorvida por ele - é conhecido por nós como o componente difuso da luz.

Mas existem algumas nuances associadas à absorção da luz - isso não acontece instantaneamente, assim que a luz toca a superfície. Desde o curso da física, sabemos que a luz pode ser descrita como um feixe de fótons com energia que se move em linha reta até perder toda a energia como resultado de uma colisão com obstáculos. Cada material consiste em micropartículas que podem interagir com um raio de luz, como mostra a figura abaixo. Essas partículas absorvem parte ou toda a energia da luz em cada colisão, convertendo-a em calor.

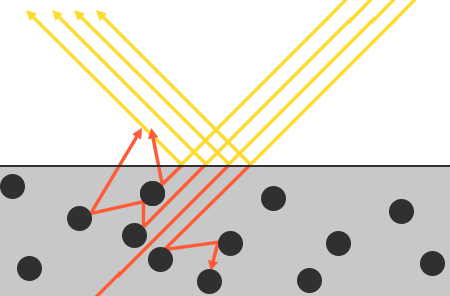
No caso geral, nem toda a energia é absorvida e a luz continua a se espalhar em direções (predominantemente) aleatórias, onde novamente colide com outras partículas até ficar sem energia ou deixar a superfície novamente. Assim, a superfície começa a reemitir raios de luz, contribuindo na forma da cor da superfície observada (difusa). Usando o PBR, assumimos de forma simplificada que toda a luz refratada é absorvida e dispersa por uma pequena área de influência, ignorando o efeito da luz dispersa que sai da superfície a uma distância dessa área. Técnicas especiais de sombreamento que levam isso em consideração, conhecidas como técnicas de espalhamento subterrâneo , melhoram muito a qualidade visual de materiais como couro, mármore, cera, mas são caras em termos de desempenho.

Sutilezas adicionais aparecem quando a luz é refratada e refletida em superfícies metálicas . As superfícies metálicas interagem de maneira diferente com a luz e as não metálicas (isto é, dielétricas). Eles obedecem às mesmas leis de refração e reflexão, com uma exceção: toda a luz refratada é absorvida pela superfície sem se espalhar, apenas a luz refletida no espelho permanece; por outras palavras, as superfícies metálicas não têm uma cor difusa. Devido a essa óbvia diferença entre metais e dielétricos, eles serão processados ​​de maneira diferente no transportador PBR no qual iremos aprofundar o curso deste artigo.

Essa diferença entre luz refletida e refratada nos leva a outra observação sobre a conservação de energia: seus valores são mutuamente exclusivos. A energia da luz refletida não pode ser absorvida pelo material. Portanto, a energia absorvida pela superfície na forma de luz refratada é a energia restante após contabilizar a luz refletida.
Usamos essa relação, calculando primeiro a parte refletida como uma porcentagem da energia dos raios incidentes refletidos pela superfície e, em seguida, a fração da luz refratada diretamente da refletida, como:

float kS = calculateSpecularComponent(...); // /  float kD = 1.0 - kS; // /  

Dessa maneira, aprendemos os significados das partes refletida e refratada, graças à lei da conservação de energia. Com essa abordagem, nem a parte refratada (difusa) nem a parte refletida excederão 1,0, garantindo que sua energia total não exceda o valor da energia luminosa incidente, o que não pudemos levar em consideração nas lições anteriores.

Equação de reflexão

O exposto acima nos leva à chamada equação de renderização : uma equação complexa inventada por caras muito inteligentes, e hoje é o melhor modelo para simular iluminação. O PBR segue estritamente uma versão mais específica dessa equação, conhecida como equação de reflexão . Para entender bem o PBR, é importante primeiro entender completamente a equação de reflexão:

$$

$$L_o (p, \ omega_o) = \ int \ limits_ \ Omega f_r (p, \ omega_i, \ omega_o) L_i (p, \ omega_i) n \ cdot \ omega_id \ omega_i$$

A princípio, parece assustador, mas vamos separá-lo gradualmente, em partes, e você verá como lentamente isso começará a fazer sentido. Para entender essa equação, teremos que nos aprofundar um pouco mais na radiometria. Radiometria é a ciência da medição da radiação eletromagnética (incluindo luz visível). Existem várias quantidades radiométricas que podemos usar para medir a iluminação, mas usaremos apenas uma relacionada à equação de reflexão, conhecida como Luminância de energia (esplendor inglês) e designada aqui pela letra L.EI é usada para quantificar a magnitude ou intensidade da luz, vindo de uma certa direção. O EJ, por sua vez, é uma combinação de várias quantidades físicas e, para que seja mais fácil imaginá-lo, focaremos em cada uma delas individualmente.

Fluxo Radiante

Fluxo de radiação ( $$$\ Phi$ ) é a potência da energia transmitida pela luz, medida em watts. A energia total da luz consiste em muitos termos para diferentes comprimentos de onda, cada um dos quais corresponde à sua própria cor do espectro. A energia emitida pela fonte de luz, neste caso, pode ser representada como uma função de todos esses comprimentos de onda. Comprimentos de onda de 390nm a 700nm compõem a parte visível do espectro, ou seja, a radiação nessa faixa pode ser percebida pelo olho humano. Na imagem abaixo, você pode ver os valores das energias para diferentes comprimentos de onda que compõem a luz do dia:

O fluxo de radiação corresponde à área sob o gráfico desta função para todos os comprimentos de onda. O uso direto de comprimentos de onda da luz como entrada em computação gráfica é impraticável, por isso recorremos a uma representação simplificada do fluxo de radiação, em vez de usar uma função de todos os comprimentos de onda, um trio de cores, conhecido como RGB (ou, como costumamos chamar, a cor da iluminação). Essa visão leva a alguma perda de informações, mas no geral afetará levemente a imagem final.

Ângulo sólido

Ângulo sólido indicado por $$$\ omega$ nos fornece o tamanho ou a área da figura projetada na esfera unitária. Você pode imaginá-lo como uma direção com um volume de:

Imagine que você está no centro de uma esfera e olhando na direção da figura. O tamanho da silhueta resultante será um ângulo sólido.

Intensidade de radiação

A força da radiação mede a quantidade de fluxo de radiação por ângulo sólido ou a força de uma fonte de luz por unidade de área definida pelo ângulo sólido. Por exemplo, para uma fonte de luz omnidirecional que emite igualmente em todas as direções, a força de radiação significa a energia da luz por área específica (ângulo sólido):

A equação que descreve a força da radiação é assim:

$$

$$I = \ frac {d \ Phi} {d \ omega}$$

, onde eu é o fluxo de radiação f por ângulo sólido $$${d \ omega}$

Conhecendo o fluxo de radiação, a força e o ângulo sólido, podemos descrever a equação do brilho da energia que descreve a energia total observada na área A, limitada pelo ângulo sólido O da luz pela força $$$\ Phi$

$$

$$L = \ frac {d ^ 2 \ Phi} {dA d \ omega \ cos \ theta}$$

O brilho da energia é a quantidade radiométrica de luz em uma área que depende do ângulo da luz incidente. $$$\ theta$ (ângulo entre a direção da luz e o normal para a superfície) através $$$cos \ theta$ : A luz é mais fraca quando emitida ao longo da superfície e mais forte quando é perpendicular a ela. Isso é semelhante aos nossos cálculos para luz difusa no tutorial sobre conceitos básicos de iluminação, pois $$$cos \ theta$ nada mais que um produto escalar entre a direção da luz e o vetor normal para a superfície:

 float cosTheta = dot(lightDir, N); 

A equação do brilho da energia é muito útil para nós, pois contém a maioria das quantidades físicas que nos interessam. Se assumirmos que o ângulo sólido ω e a área A são infinitesimais, podemos usar o EE para medir o fluxo de um raio de luz por um ponto no espaço. Isso nos permitirá calcular o EI de um único raio de luz atuando em um único ponto (fragmento); na verdade, traduzimos o ângulo sólido $$$\ omega$ no vetor de direção $$$\ omega$ e $$$A$ direto ao ponto $$$p$ . Assim, podemos usar diretamente o EI em nossos shaders para calcular a contribuição de um único raio de luz para cada fragmento.

De fato, quando se trata de EE, geralmente estamos interessados ​​em todo o incidente de luz recebido no ponto p, que é a soma de todo o EE, e é conhecido como irradiância. Conhecendo o IE e a irradiação, podemos retornar à equação de reflexão:

$$

$$L_o (p, \ omega_o) = \ int \ limits_ \ Omega f_r (p, \ omega_i, \ omega_o) L_i (p, \ omega_i) n \ cdot \ omega_id \ omega_i$$

Agora sabemos que $$$L$ na equação de renderização é o EI para algum ponto na superfície p e algum ângulo sólido infinitamente pequeno da luz que chega $$$\ omega_i$ , que pode ser considerado como um vetor de direção de entrada $$$\ omega_i$ . Lembre-se de que a energia é multiplicada por $$$cos \ theta$ - o ângulo entre a direção da incidência da luz e o normal à superfície, expresso na equação de reflexão do produto $$$n \ cdot \ omega_i$ . A equação de reflexão calcula a soma do IE refletido $$$L_o (p, \ omega_o)$ pontos $$$p$ para $$$ω_o$ , que é a direção de saída para o observador. Ou então: $$$L_o$ mede a irradiância refletida de um ponto $$$p$ se visto de $$$\ omega_o$ .

Como a equação de reflexão é baseada na irradiação, que é a soma de toda a radiação recebida, medimos a luz não apenas de uma direção de luz recebida, mas de todas as direções de luz recebidas no hemisfério $$$\ Omega$ centrado em $$$p$ . Pode ser descrito como meia esfera orientada ao longo da superfície normal $$$n$ :

Para calcular a soma de todos os valores dentro da região, ou, no caso de um hemisfério, volume, integramos a equação em todas as direções recebidas $$$d \ omega_i$ dentro do hemisfério $$$\ Omega$ . Como não há solução analítica para a equação de renderização e a equação de reflexão, resolveremos a integral numericamente. Isso significa que obteremos resultados para pequenos passos discretos da equação de reflexão do hemisfério $$$\ Omega$ e calcule a média sobre o tamanho da etapa. Isso é chamado de soma de Riemann , que podemos representar aproximadamente com o seguinte código:

 int steps = 100; float sum = 0.0f; vec3 P = ...; vec3 Wo = ...; vec3 N = ...; float dW = 1.0f / steps; for(int i = 0; i < steps; ++i) { vec3 Wi = getNextIncomingLightDir(i); sum += Fr(P, Wi, Wo) * L(P, Wi) * dot(N, Wi) * dW; } 

dW para cada etapa discreta pode ser considerado como $$$d \ omega_i$ na equação de reflexão. Matematicamente $$$d \ omega_i$ é o diferencial pelo qual calculamos a integral e, embora não seja o mesmo que dW no código (como essa é uma etapa discreta da soma de Riemann), podemos considerá-la como tal para facilitar o cálculo. Lembre-se de que o uso de etapas discretas sempre fornecerá um valor aproximado, não o valor exato da integral. Um leitor atento perceberá que podemos aumentar a precisão da soma de Riemann aumentando o número de etapas.

A equação de reflexão soma a radiação de todas as direções de luz recebidas $$$\ omega_i$ hemisfério $$$\ Omega$ que chega ao ponto $$$p$ e retorna a quantidade de luz refletida $$$L_o$ em direção ao espectador. A radiação recebida pode vir de fontes de luz com as quais já estamos familiarizados ou de mapas ambientais que determinam o EI de cada direção de entrada, sobre a qual falaremos no tutorial do IBL.

Agora, o único desconhecido à esquerda é o símbolo $$$f_r$ , conhecida como função BRDF ou função de refletância de dois feixes , que escala (ou pesa) o valor da radiação recebida com base nas propriedades do material da superfície.

BRDF

BRDF é uma função que aceita a direção da luz incidente. $$$\ omega_i$ , direção ao observador $$$\ omega_o$ normal à superfície $$$n$ e parâmetro $$$a$ , que é a rugosidade da superfície. O BRDF aproxima o quanto cada feixe de luz individual $$$\ omega_i$ contribui para a luz refletida final de uma superfície opaca, levando em consideração as propriedades de seu material. Por exemplo, se a superfície for completamente lisa (quase como um espelho), a função BRDF retornará 0,0 para todos os raios de luz recebidos $$$\ omega_i$ exceto um com o mesmo ângulo (após reflexão) que o feixe $$$\ omega_o$ para o qual a função retornará 1.0.

O BRDF aproxima as propriedades refletivas e de refração de um material com base na teoria das micro faces mencionada anteriormente. Para que o BRDF seja fisicamente plausível, ele deve obedecer à lei de conservação de energia, ou seja, a energia total da luz refletida nunca deve exceder a energia da luz incidente. Tecnicamente, o modelo de Blinn-Fong é considerado um BRDF aceitando o mesmo $$$\ omega_i$ e $$$\ omega_o$ na entrada. No entanto, o modelo de Blinn-Fong não é considerado fisicamente correto, pois não garante o cumprimento da lei de conservação de energia. Existem vários BRDFs fisicamente corretos para aproximar a resposta da superfície à iluminação. No entanto, quase todos os pipelines gráficos em tempo real usam o BRDF, conhecido como Cook-Torrance BRDF .

O Cook-Torrens BRDF contém uma parte difusa e uma espelho:

$$

$$f_r = k_df_ {lambert} + k_sf_ {cozinhe - torrance}$$

aqui $$$k_d$ - fração refratada da energia luminosa recebida, $$$k_s$ - refletido. O lado esquerdo do BRDF contém a parte difusa da equação, aqui indicada como $$$f_ {lambert}$ . Esta é a chamada dispersão de Lambert. É semelhante ao que usamos para iluminação difusa e é constante:

$$

$$f_ {lambert} = \ frac {c} {\ pi}$$

onde $$$c$ - albedo ou cor da superfície (textura difusa da superfície). Divisão por $$$\ pi$ necessário para normalizar a luz dispersa, uma vez que a integral anteriormente indicada contendo BRDF é multiplicada por $$$\ pi$ (chegaremos a isso no tutorial do IBL).

Você pode se surpreender ao ver como essa dispersão lambertiana se assemelha à expressão para iluminação difusa que usamos anteriormente: a cor da superfície multiplicada pelo produto escalar entre a superfície normal e a direção da luz. O produto escalar ainda está presente, mas inferido do BRDF, uma vez que temos $$$n \ cdot \ omega_i$ na integral $$$L_o$ .

Existem várias equações para a parte difusa do BRDF que parecem mais realistas, mas são mais caras em termos de desempenho. Além disso, como os Jogos Épicos concluíram: a dispersão lambertiana é suficiente para a maioria dos propósitos de renderização em tempo real.

A parte espelhada do Cook-Torrens BRDF é ligeiramente melhorada e é descrita como:

$$

$$f_ {cook - torrance} = \ frac {DFG} {4 (\ omega_o \ cdot n) (\ omega_i \ cdot n)}$$

É composto por três funções e um coeficiente de padronização no denominador. Cada uma das letras D, F e G representa um certo tipo de função que se aproxima de uma certa parte das propriedades refletivas da superfície. Eles são conhecidos como a função de distribuição normal (NDF), a equação de Fresnel e a função Geometria:

• Função de distribuição normal: aproxima o número de microfaciais de superfície orientadas ao longo do vetor mediano, com base na rugosidade da superfície; Esta é a principal função que aproxima as micro faces.
• Função Geometria: descreve a propriedade de sombreamento automático das micro faces. Quando a superfície é bastante rugosa, algumas micro-faces da superfície podem se sobrepor a outras, reduzindo assim a quantidade de luz refletida pela superfície.
• Equação de Fresnel: descreve o coeficiente de reflexão da superfície em diferentes ângulos.

Cada uma dessas funções é uma aproximação do seu equivalente físico e, para elas, existem várias implementações destinadas a uma aproximação mais precisa do modelo físico subjacente; alguns dão resultados mais realistas, outros são mais eficazes em termos de desempenho. Brian Caris, da Epic Games, fez muitas pesquisas sobre diferentes tipos de aproximações, sobre as quais você pode aprender mais aqui . Usaremos as mesmas funções que no Unreal Engine 4 da Epic Games, a saber: Trowbridge-Reitz GGX para D, aproximação Fresnel-Schlick para F e Smith e Schlick-GGX para G.

Função de distribuição normal

A função de distribuição normal D aproxima estatisticamente a área de superfície relativa das micro faces orientadas com precisão ao longo do vetor mediano $$$h$ . Existem muitos NDFs que determinam a aproximação estatística do alinhamento geral das micro faces, levando em consideração algum parâmetro de rugosidade. Usaremos um conhecido como Trowbridge-Reitz GGX:

$$

$$NDF_ {GGXTR} (n, h, \ alpha) = \ frac {\ alpha ^ 2} {\ pi ((n \ cdot h) ^ 2 (\ alpha ^ 2−1) +1) ^ 2}$$

aqui $$$h$ É o vetor mediano, $$$\ alpha$ - valor da rugosidade da superfície. Se escolhermos $$$h$ como o vetor mediano entre o normal para a superfície e a direção da luz, alterando o parâmetro de rugosidade, obtemos a seguinte imagem:

Quando a rugosidade é pequena (isto é, a superfície é lisa), as micro faces orientadas na direção do vetor mediano são concentradas em um raio pequeno. Devido a essa alta concentração, o NDF fornece um ponto muito brilhante. Em uma superfície rugosa, onde as micro faces são orientadas em direções mais aleatórias, você encontrará um número muito maior de micro faces orientadas na direção do vetor mediano $$$h$ mas localizado em um raio maior, o que torna a cor exata mais cinza.

No código GLSL, a função de distribuição normal Trowbridge-Reitz GGX será semelhante a esta:

 float DistributionGGX(vec3 N, vec3 H, float a) { float a2 = a*a; float NdotH = max(dot(N, H), 0.0); float NdotH2 = NdotH*NdotH; float nom = a2; float denom = (NdotH2 * (a2 - 1.0) + 1.0); denom = PI * denom * denom; return nom / denom; } 

Função de geometria

A função geometria aproxima estatisticamente a área relativa da superfície, onde suas irregularidades microscópicas se sobrepõem, o que impede a penetração dos raios de luz.

Como no caso do NDF, a função geometria aceita o coeficiente de rugosidade da superfície como uma entrada, o que neste caso significa o seguinte: superfícies mais ásperas terão maior probabilidade de sombreamento de micro-faces. A função de geometria que usaremos é uma combinação das aproximações GGX e Schlick-Beckmann, e é conhecida como Schlick-GGX:

$$

$$G_ {SchlickGGX} (n, v, k) = \ frac {n \ cdot v} {(n \ cdot v) (1 - k) + k}$$

Aqui $$$k$ é uma redesignação $$$\ alpha$ dependendo se usamos a função de geometria para iluminação direta ou iluminação IBL:

$$

$$k_ {direct} = \ frac {(\ alpha + 1) ^ 2} {8}$$

$$

$$k_ {IBL} = \ frac {\ alpha ^ 2} {2}$$

Observe que o valor $$$\ alpha$ pode variar dependendo de como o seu motor traduz a rugosidade em $$$\ alpha$ . Nas lições a seguir, discutiremos em detalhes como e onde essa transferência se torna relevante.

Para aproximar efetivamente a geometria, precisamos levar em consideração a direção da vista (geometria sobreposta) e o vetor de direção da luz (auto-sombreamento da geometria). Podemos considerar os dois casos usando o método Smith :

$$

$$G (n, v, l, k) = G_ {sub} (n, v, k) G_ {sub} (n, l, k)$$

Usando o método Smith com Schlick-GGX como $$$G_ {sub}$ dá a seguinte imagem com rugosidade diferente R:

A função geometria é um fator entre [0,0, 1,0], onde branco (ou 1,0) significa que não há sombreamento das micro-faces e preto (ou 0,0) significa sombreamento completo das micro-faces.

No GLSL, uma função de geometria é convertida no seguinte código:

 float GeometrySchlickGGX(float NdotV, float k) { float nom = NdotV; float denom = NdotV * (1.0 - k) + k; return nom / denom; } float GeometrySmith(vec3 N, vec3 V, vec3 L, float k) { float NdotV = max(dot(N, V), 0.0); float NdotL = max(dot(N, L), 0.0); float ggx1 = GeometrySchlickGGX(NdotV, k); float ggx2 = GeometrySchlickGGX(NdotL, k); return ggx1 * ggx2; } 

Equação de Fresnel

A equação de Fresnel descreve a proporção de luz refletida e refratada, que depende do ângulo em que olhamos para a superfície. Quando a luz atinge uma superfície, a equação de Fresnel nos fornece a porcentagem de luz refletida com base no ângulo em que vemos essa superfície. A partir dessa proporção de reflexão e da lei de conservação de energia, podemos obter diretamente a parte refratada da luz, que será igual à energia restante.

Cada superfície ou material possui um nível de refletividade básica , observado ao olhar diretamente para a superfície, mas se você olha para a superfície em ângulo, todas as reflexões se tornam mais visíveis. Você pode verificar isso sozinho, observando sua mesa provavelmente de madeira ou metal primeiro perpendicularmente e depois em um ângulo próximo a 90 graus. Você verá que as reflexões se tornam muito mais visíveis. Todas as superfícies, teoricamente, refletem completamente a luz quando vistas a partir delas em um ângulo ideal de 90 graus. Esse efeito é denominado Fresnel e é descrito pela equação de Fresnel .

A equação de Fresnel é bastante complexa, mas, felizmente, pode ser simplificada usando a aproximação de Fresnel-Schlick :

$$

$$F_ {Schlick} (h, v, F_0) = F_0 + (1 - F_0) (1− (h \ cdot v)) ^ 5$$

$$$F_0$ representa a refletividade básica da superfície, que calculamos usando algo chamado índices de refração ou IORs (índices de refração) e, como você pode ver na superfície da esfera, quanto mais próxima a direção de visualização dos limites da esfera visível (o ângulo entre a direção de visualização e a mediana 90 ), , , :

, . , - . (), , . , ( $$$F_0$ ) ( 0 , ) -, , .

. , , :

: 0.17, , , ( ) 0.5 1.0. , “”, $$$F_0$ RGB ( ).

, metallic workflow: , (metalness), , .

: , ; , . , 0.0 1.0. - , , , . , .

$$$F_0$ , , - , , . :

 vec3 F0 = vec3(0.04); F0 = mix(F0, surfaceColor.rgb, metalness); 

, . , $$$F_0$ . 0.04 . , , , F0 . , , .

- :

 vec3 fresnelSchlick(float cosTheta, vec3 F0) { return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0); } 

cosTheta .

-

BRDF - :

$$

$$L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi}+k_s\frac{DFG}{4(\omega_o\cdot n)(\omega_i \cdot n)}) L_i(p, \omega_i)n\cdot \omega_i d\omega_i$$

. , , F . $$$k_s$ , , $$$k_s$ . , :

$$

$$L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi}+\frac{DFG}{4(\omega_o\cdot n)(\omega_i \cdot n)}) L_i(p, \omega_i)n\cdot \omega_i d\omega_i$$

, PBR. , , . , , .

PBR

, PBR, , , PBR. , PBR, . , : , .

, PBR, :

: , . , . , ; .

: , , . , , .

: . , PBR-, , : .

: , . . , . PBR- , , (1.0 — ) .

AO (ambient occlusion) : AO . , , . AO , . . , 3D-.

. PBR, , . , PBR, PBR-, , , .

• Background: Physics and Math of Shading by Naty Hoffmann: , , ; PBR, must-read .
• Real shading in Unreal Engine 4 : PBR, Epic Games Unreal Engine 4. PBR, , .
• Marmoset: PBR Theory : PBR. , , , .
• Coding Labs: Physically based rendering : , PBR.
• Coding Labs: Physically Based Rendering — Cook–Torrance : BRDF -
• Wolfire Games — Physically based rendering : PBR Lukas Orsvärn.
• [SH17C] Physically Based Shading : shadertoy (: ) Krzysztof Narkowi, PBR.