O princípio da menor ação. Parte 2

Da última vez , examinamos brevemente um dos princípios físicos mais notáveis ​​- o princípio da menor ação e estabelecemos um exemplo que, ao que parece, o contradiz. Neste artigo, trataremos desse princípio com mais detalhes e veremos o que acontece neste exemplo.

Desta vez, precisamos de um pouco mais de matemática. No entanto, tentarei definir a parte principal do artigo novamente em um nível elementar. Destacarei pontos um pouco mais rigorosos e complexos, que podem ser ignorados sem prejuízo do entendimento básico do artigo.

Condições de contorno

Começaremos com o objeto mais simples - uma bola se movendo livremente no espaço, sobre a qual nenhuma força atua. Tal bola, como é conhecida, se move de maneira uniforme e retilínea. Para simplificar, suponha que ele se mova ao longo do eixo $$$x$ :

Para descrever com precisão seu movimento, como regra, as condições iniciais são especificadas. Por exemplo, é especificado que no momento inicial do tempo $$$t_A$ a bola estava em um ponto $$$A$ com coordenada $$$x_A$ e tinha velocidade $$$v_A$ . Depois de definir as condições iniciais dessa forma, determinamos exclusivamente o movimento adicional da bola - ela se moverá a uma velocidade constante e sua posição no momento $$$t$ será igual à posição inicial mais a velocidade multiplicada pelo tempo decorrido: $$$x (t) = x_A + v_A \ cdot (t-t_A)$ . Essa maneira de definir as condições iniciais é muito natural e intuitivamente familiar. Pedimos todas as informações necessárias sobre o movimento da bola no momento inicial e, em seguida, seu movimento é determinado pelas leis de Newton.

No entanto, esta não é a única maneira de especificar o movimento da bola. Outra maneira alternativa é definir a posição da bola em dois pontos diferentes no tempo. $$$t_A$ e $$$t_B$ . I.e. pergunte isso:

1) no tempo $$$t_A$ a bola estava em um ponto $$$A$ (com coordenadas $$$x_A$ );
2) no tempo $$$t_B$ a bola estava em um ponto $$$B$ (com coordenadas $$$x_B$ )

A expressão "estava em um ponto $$$A$ "Não significa que a bola descansou em um ponto $$$A$ . No tempo $$$t_A$ ele poderia voar sobre um ponto $$$A$ . Isso significa que sua posição no momento $$$t_A$ coincidiu com um ponto $$$A$ . O mesmo se aplica ao ponto $$$B$ .

Essas duas condições também determinam exclusivamente o movimento da bola. Seu movimento é fácil de calcular. Para satisfazer ambas as condições, a velocidade da bola deve obviamente ser $$$(x_B-x_A) / (t_B-t_A)$ . Posição da bola no tempo $$$t$ será igual à posição inicial mais a velocidade multiplicada pelo tempo decorrido:

$$

$$x (t) = x_A + ((x_B-x_A) / (t_B-t_A)) \ cdot (t-t_A)$$

Observe que nas condições do problema não precisamos definir a velocidade inicial. É determinado exclusivamente a partir das condições 1) e 2).

Definir condições da segunda maneira parece incomum. Talvez não esteja claro por que, em geral, pode ser necessário perguntar a eles dessa forma. No entanto, no princípio da menor ação, são precisamente as condições nas formas 1) e 2) que são usadas, e não na forma de definir a posição inicial e a velocidade inicial.

Trajetória de menor ação

Agora vamos desviar um pouco do real movimento livre da bola e considerar o seguinte problema puramente matemático. Suponha que tenhamos uma bola que possamos mover manualmente da maneira que quisermos. Nesse caso, precisamos preencher as condições 1) e 2). I.e. entre $$$t_A$ e $$$t_B$ nós temos que movê-lo do ponto $$$A$ direto ao ponto $$$B$ . Isso pode ser feito de maneiras completamente diferentes. Cada um desses métodos será chamado de trajetória da bola e pode ser descrito pela função da posição da bola no tempo $$$x (t)$ . Adiamos várias dessas trajetórias no gráfico da dependência da posição da bola no tempo:

Por exemplo, podemos mover a bola na mesma velocidade igual a $$$(x_B-x_A) / (t_B-t_A)$ (caminho verde). Ou podemos mantê-lo no meio ponto $$$A$ e depois dobrar a velocidade para ir ao ponto $$$B$ (trajetória azul). Você pode movê-lo primeiro na direção oposta. $$$B$ lado e depois já passar para $$$B$ (trajetória marrom). Você pode movê-lo para frente e para trás (trajetória vermelha). Em geral, você pode movê-lo como quiser, se apenas as condições 1) e 2) forem observadas.

Para cada uma dessas trajetórias, podemos combinar um número. Em nosso exemplo, ou seja, na ausência de forças agindo na bola, esse número é igual à energia cinética total acumulada durante todo o tempo de seu movimento no intervalo entre $$$t_A$ e $$$t_B$ e é chamado de ação.

Nesse caso, a palavra energia cinética "acumulada" não transmite com precisão o significado. Na realidade, a energia cinética não se acumula em lugar algum; a acumulação é usada apenas para calcular a ação para a trajetória. Em matemática, para essa acumulação, existe um conceito muito bom - a integral:

$$

$$S = \ int \ limits_ {t_A} ^ {t_B} Tdt$$

A ação é geralmente indicada pela letra $$$S$ . Símbolo $$$T$ significa energia cinética. Essa integral significa que a ação é igual à energia cinética acumulada da bola durante um período de tempo entre $$$t_A$ antes $$$t_B$ .

Como exemplo, vamos pegar uma bola com 1 kg., Defina algumas condições de contorno e calcule a ação para duas trajetórias diferentes. Deixe o ponto $$$B$ fica a 1 metro do ponto $$$A$ e tempo $$$t_B$ distante do tempo $$$t_A$ por 1 segundo. I.e. devemos mover a bola que no momento inicial estava no ponto $$$A$ , em um segundo a uma distância de 1 m ao longo do eixo $$$x$ .

No primeiro exemplo (trajetória verde), movemos a bola uniformemente, ou seja, com a mesma velocidade, que, obviamente, deve ser igual a: $$$v = 1$ m / s A energia cinética da bola em cada momento é igual a: $$$T = mv ^ 2/2$ = 1/2 J. Em um segundo, 1/2 J acumulará $$$\ cdot$ com energia cinética. I.e. válido para essa trajetória é: $$$S = 1/2$ J $$$\ cdot$ s

Agora não vamos transferir a bola imediatamente do ponto $$$A$ direto ao ponto $$$A$ e mantenha-o em um ponto por meio segundo $$$A$ e, durante o tempo restante, transferimos uniformemente para o ponto $$$B$ . No primeiro meio segundo, a bola está em repouso e sua energia cinética é zero. Portanto, a contribuição para a ação dessa parte da trajetória também é igual a zero. No segundo meio segundo, transferimos a bola em velocidade dupla: $$$v = 2$ m / s A energia cinética será igual a $$$T = mv ^ 2/2$ = 2 J. A contribuição desse período para a ação será 2 J multiplicada por meio segundo, ou seja, 1 J $$$\ cdot$ s Portanto, a ação geral para essa trajetória é igual a $$$S = 1$ J $$$\ cdot$ s

Da mesma forma, qualquer outra trajetória com as condições de contorno especificadas 1) e 2) corresponde a um determinado número igual à ação de uma determinada trajetória. Entre todas essas trajetórias, há uma trajetória em que a ação é a menor. Pode-se provar que essa trajetória é verde, ou seja, movimento uniforme da bola. Para qualquer outra trajetória, por mais complicada que seja, a ação será superior a 1/2.

Em matemática, essa comparação para cada função de um determinado número é chamada de funcional. Muitas vezes, em física e matemática, tarefas como a nossa surgem, ou seja, para encontrar uma função para a qual o valor de uma determinada funcionalidade é mínimo. Por exemplo, uma das tarefas de grande importância histórica para o desenvolvimento da matemática é o problema do bachistocrono . I.e. encontrar uma curva ao longo da qual a bola rola mais rápido. Novamente, cada curva pode ser representada pela função h (x) e cada função pode receber um número, neste caso o tempo de rolagem da bola. Novamente, o problema se resume a encontrar uma função para a qual o valor da funcional é mínimo. A área da matemática que lida com esses problemas é chamada de cálculo de variações.

Princípio da menor ação

Nos exemplos discutidos acima, temos duas trajetórias especiais obtidas de duas maneiras diferentes.

A primeira trajetória é obtida das leis da física e corresponde à trajetória real de uma bola livre, que não é afetada por nenhuma força e para a qual as condições de contorno são dadas nas formas 1) e 2).

A segunda trajetória é obtida do problema matemático de encontrar uma trajetória com determinadas condições de contorno 1) e 2), para as quais a ação é mínima.

O princípio da menor ação afirma que essas duas trajetórias devem coincidir. Em outras palavras, se se sabe que a bola se moveu de tal maneira que as condições de contorno 1) e 2) foram satisfeitas, então necessariamente se moveu ao longo de um caminho para o qual a ação é mínima em comparação com qualquer outro caminho com as mesmas condições de contorno.

Pode-se considerar isso uma mera coincidência. Existem muitos problemas nos quais trajetórias uniformes e linhas retas aparecem. No entanto, o princípio da menor ação é um princípio muito geral, válido em outras situações, por exemplo, para o movimento da bola em um campo gravitacional uniforme. Para fazer isso, você só precisa substituir a energia cinética pela diferença entre energia cinética e energia potencial. Essa diferença é chamada de função Lagrangiana ou Lagrange e a ação agora se torna igual ao Lagrangiano acumulado total. De fato, a função Lagrange contém todas as informações necessárias sobre as propriedades dinâmicas do sistema.

Se lançarmos uma bola em um campo de gravidade uniforme, para que ela passe um ponto $$$A$ no tempo $$$t_A$ e voou direto ao ponto $$$B$ no tempo $$$t_B$ , então ele, de acordo com as leis de Newton, terá uma parábola. É essa parábola que coincide com as trajetórias para as quais a ação será mínima.

Assim, para um corpo que se move em um campo potencial, por exemplo, no campo gravitacional da Terra, a função Lagrange é igual a: $$$L = T (v) -V (x, y, z)$ . Energia cinética $$$T$ depende da velocidade do corpo e do potencial - de sua posição, ou seja, coordenadas $$$x, y, z$ . Na mecânica analítica, todo o conjunto de coordenadas que determina a posição de um sistema é geralmente indicado por uma letra $$$q$ . Para uma bola se movendo livremente em um campo gravitacional, $$$q$ significa coordenadas $$$x$ , $$$y$ e $$$z$ .

Para indicar a taxa de variação de uma quantidade, na física, muitas vezes, eles simplesmente acabam com essa quantidade. Por exemplo $$$\ ponto x$ indica a taxa de mudança de coordenadas $$$x$ ou, em outras palavras, a velocidade do corpo na direção $$$x$ . Usando essas convenções, a velocidade de nossa bola na mecânica analítica é indicada como $$$\ ponto q$ . I.e. $$$\ ponto q$ componentes de velocidade média $$$v_x, v_y, v_z$ .

Como a função Lagrange depende da velocidade e das coordenadas, também pode depender explicitamente do tempo (depende explicitamente do tempo significa que o valor $$$L$ em momentos diferentes, diferentes, nas mesmas velocidades e posições da bola), então a ação em geral é escrita como

$$

$$S = \ int \ limits_ {t_A} ^ {t_B} L (\ ponto q, q, t) dt$$

Nem sempre mínimo

No entanto, no final da parte anterior, vimos um exemplo em que o princípio de menos ação claramente não funciona. Para fazer isso, pegamos novamente uma bola livre, que não é afetada por nenhuma força, e colocamos uma parede de mola ao lado dela.
Estabelecemos as condições de contorno de modo que os pontos $$$A$ e $$$B$ combinar. I.e. e no tempo $$$t_A$ e no tempo $$$t_B$ a bola deve estar no mesmo ponto $$$A$ . Uma das trajetórias possíveis será a posição da bola no lugar. I.e. o tempo todo entre $$$t_A$ e $$$t_B$ ele vai ficar em um ponto $$$A$ . A energia cinética e potencial neste caso será igual a zero, portanto a ação para essa trajetória também será igual a zero.

A rigor, a energia potencial pode ser tomada não igual a zero, mas a qualquer número, já que a diferença de energia potencial em diferentes pontos do espaço é importante. No entanto, uma mudança no valor da energia potencial não afeta a busca de uma trajetória com ação mínima. É apenas que, para todas as trajetórias, o valor da ação mudará no mesmo número, e a trajetória com ação mínima permanecerá a trajetória com ação mínima. Por conveniência, para nossa bola, escolheremos a energia potencial igual a zero.

Outra possível trajetória física com as mesmas condições de contorno seria uma trajetória em que a bola voa primeiro para a direita, passando um ponto $$$A$ no tempo $$$t_A$ . Então ele colide com a mola, comprime, a mola se endireita, empurra a bola para trás e novamente ele voa além do ponto $$$A$ . Você pode escolher a velocidade da bola para que, batendo na parede, voe um ponto $$$A$ bem no momento $$$t_B$ . A ação com essa trajetória será basicamente igual à energia cinética acumulada durante o vôo entre o ponto $$$A$ e parede e costas. Haverá um certo período de tempo em que a bola comprime a mola e sua energia potencial aumenta e, durante esse período, a energia potencial fará uma contribuição negativa para a ação. Mas esse período de tempo não será muito grande e a ação não será muito reduzida.



A figura mostra as duas trajetórias fisicamente possíveis da bola. O caminho verde corresponde a uma bola em repouso, enquanto o azul corresponde a uma bola quicando na parede da primavera.

No entanto, apenas um deles tem um efeito mínimo, ou seja, o primeiro! A segunda trajetória tem mais ação. Acontece que nesse problema existem duas trajetórias fisicamente possíveis e apenas uma com ação mínima. I.e. neste caso, o princípio de menos ação não funciona.

Pontos estacionários

Para entender qual é o problema aqui, vamos nos desviar do princípio da menor ação por enquanto e assumir as funções usuais. Vamos dar uma função $$$y (x)$ e desenhe sua agenda:

No gráfico, marquei quatro pontos especiais em verde. O que é comum a esses pontos? Imagine que um gráfico de funções é um slide real no qual uma bola pode rolar. Os quatro pontos marcados são especiais, pois se você instalar a bola exatamente nesse ponto, ela não rolará em lugar algum. Em todos os outros pontos, por exemplo, no ponto E, ele não será capaz de permanecer no lugar e começará a deslizar para baixo. Tais pontos são chamados estacionários. Encontrar esses pontos é uma tarefa útil, pois qualquer função máxima ou mínima, se ela não apresentar dobras acentuadas, deve ser um ponto estacionário.

Se classificarmos esses pontos com mais precisão, o ponto A é o mínimo absoluto da função, ou seja, seu valor é menor que qualquer outro valor da função. Ponto B - não é um máximo nem um mínimo e é chamado de ponto de sela. O ponto C é chamado de máximo local, ou seja, o valor nele é maior que nos pontos vizinhos da função. E o ponto D é um mínimo local, ou seja, o valor nele é menor que nos pontos vizinhos da função.

A busca por esses pontos é realizada por um ramo da matemática chamado análise matemática. Por outro lado, às vezes é chamada de análise do infinitesimal, pois sabe trabalhar com quantidades infinitesimais. Do ponto de vista da análise matemática, os pontos estacionários têm uma propriedade especial, graças à qual são encontrados. Para entender o que é essa propriedade, precisamos entender como é a função a distâncias muito pequenas desses pontos. Para fazer isso, pegamos um microscópio e olhamos para nossos pontos. A figura mostra como é a função nas proximidades de vários pontos com diferentes ampliações.

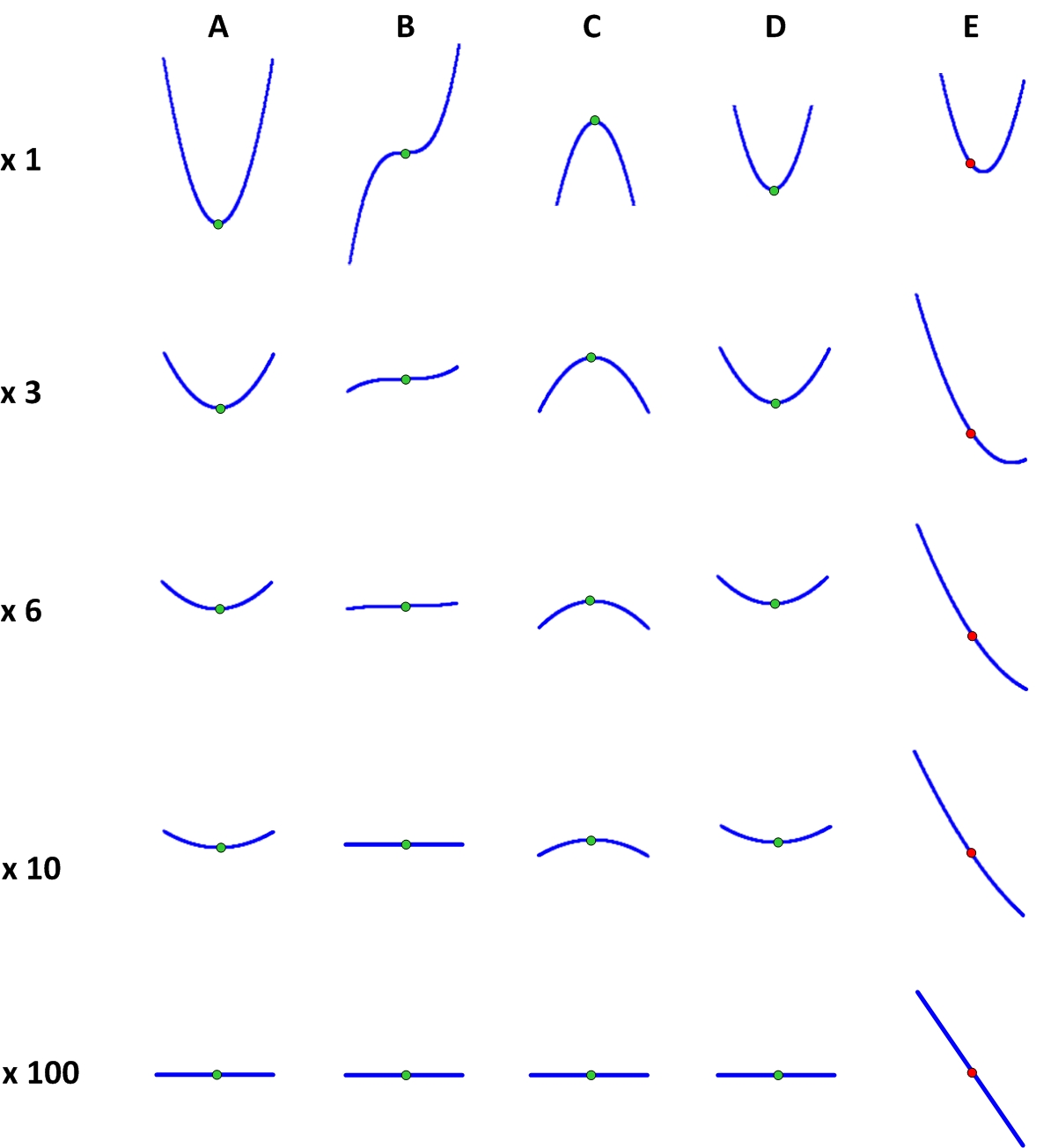
Pode-se observar que, com uma ampliação muito grande (ou seja, com desvios muito pequenos x), os pontos estacionários parecem exatamente os mesmos e diferem muito do ponto não estacionário. É fácil entender qual é essa diferença: o gráfico da função em um ponto estacionário com aumento torna-se uma linha estritamente horizontal e, em um não-estacionário, torna-se uma linha inclinada. É por isso que uma bola montada em um ponto estacionário não rola.

A horizontalidade da função no ponto estacionário pode ser expressa de maneira diferente: a função no ponto estacionário praticamente não muda com uma mudança muito pequena em seu argumento $$$x$ , mesmo em comparação com o próprio argumento. A função está em um ponto não estacionário com uma pequena alteração $$$x$ varia em proporção a $$$x$ . E quanto maior o ângulo da função, mais forte ela muda ao mudar $$$x$ . De fato, a função com tamanho crescente se torna cada vez mais semelhante à tangente ao gráfico no ponto em questão.

Em linguagem matemática estrita, a expressão “função praticamente não muda em um ponto $$$x_0$ com muito pouca mudança $$$x$ "Significa que a razão entre a mudança de função e a mudança de seu argumento $$$Δy / Δx$ tende a 0 em $$$∆x$ tendendo a 0:

$$$$ display $$ \ lim_ {Δx \ a 0} \ frac {Δy (x_0)} {Δx} = \ lim_ {x \ a 0} \ frac {y (x_0 + Δx) -y (x_0) } {∆x} = 0 $$ exibir $$

Para um ponto não estacionário, essa proporção tende a um número diferente de zero, que é igual à inclinação da função nesse ponto. O mesmo número é chamado de derivada da função em um determinado ponto. A derivada da função mostra a rapidez com que a função muda perto de um determinado ponto com uma pequena alteração no argumento $$$x$ . Assim, pontos estacionários são pontos nos quais a derivada da função é 0.

Trajetórias estacionárias

Por analogia com os pontos estacionários, o conceito de trajetórias estacionárias pode ser introduzido. Lembre-se de que cada trajetória corresponde a um determinado valor de ação, ou seja, algum número. Então pode haver tal trajetória que, para trajetórias próximas a ela com as mesmas condições de contorno, os valores de ação correspondentes praticamente não diferem da ação da própria trajetória estacionária. Essa trajetória é chamada de estacionária. Em outras palavras, qualquer trajetória próxima ao estacionário terá um valor de ação que difere muito pouco da ação para essa trajetória estacionária.

Novamente, na linguagem matemática "pouco diferente" tem o seguinte significado exato. Digamos que temos um funcional $$$S (x (t))$ para funções com as condições de contorno necessárias 1) e 2), ou seja, $$$x (t_A) = A$ e $$$x (t_B) = B$ . Suponha que a trajetória $$$x (t)$ - estacionário.

Podemos assumir qualquer outra função. $$$g (t)$ de tal forma que, no final, assume zero valores, ou seja, $$$g (t_A)$ = $$$g (t_B)$ = 0. Pegue também a variável $$$ε$ o que faremos cada vez menos. Destas duas funções e variáveis $$$ε$ nós podemos fazer uma terceira função $$$x '(t) = x (t) + εg (t)$ , $$$f'(t_A)=A$ e $$$f'(t_B)=B$ . $$$ε$ , $$$x'(t)$ , $$$x(t)$ .

$$$ε$ $$$x'(t)$ $$$x(t)$ $$$ε$ . I.e.

$$

$$\lim_{ε \to 0} \frac {S(x'(t))-S(x(t))}ε=\lim_{ε \to 0} \frac {S(x(t)+εg(t))-S(x(t))}ε = 0$$

$$$g(t)$ , $$$g(t_A)$ = $$$g(t_B)$ = 0.

(, , ) $$$δS$ . «» « ».

$$$δS=0$ .

O método de encontrar funções estacionárias (não apenas para o princípio da menor ação, mas também para muitos outros problemas) foi encontrado por dois matemáticos - Euler e Lagrange. Acontece que a função estacionária, cuja funcional é expressa por uma integral semelhante à integral de ação, deve satisfazer uma certa equação, que agora é chamada de equação de Euler-Lagrange.

Princípio estacionário

A situação com um mínimo de ação para trajetórias é semelhante à situação com um mínimo para funções. Para que a trajetória tenha o menor efeito, ela deve ser uma trajetória estacionária. No entanto, nem todas as trajetórias estacionárias são trajetórias com ação mínima. Por exemplo, uma trajetória estacionária pode ter ação mínima localmente. I.e.sua ação será menor que a de qualquer outra trajetória adjacente. No entanto, em algum lugar distante, pode haver outras trajetórias para as quais a ação será ainda menor.

Acontece que os corpos reais podem não necessariamente se mover ao longo de trajetórias com o mínimo de ação. Eles podem se mover ao longo de um conjunto mais amplo de trajetórias especiais, a saber, trajetórias estacionárias. I.e.a verdadeira trajetória do corpo será sempre estacionária. Portanto, o princípio da menor ação é mais corretamente chamado de princípio da ação estacionária. No entanto, de acordo com a tradição estabelecida, muitas vezes é chamado de princípio de menor ação, implicando para isso não apenas a minoria, mas também a estacionariedade das trajetórias.

Agora podemos escrever o princípio da ação estacionária em uma linguagem matemática, como geralmente é escrita em livros didáticos:

$$

$$δS=δ\int\limits_{t_A}^{t_B} L(\dot q,q,t)dt = 0$$

.

Aqui $$$q$São coordenadas generalizadas, ou seja, um conjunto de variáveis ​​que especificam exclusivamente a posição do sistema.
$$$\dot q$ - a taxa de variação das coordenadas generalizadas.
$$$L(\dot q,q,t)$ - a função Lagrange, que depende das coordenadas generalizadas, suas velocidades e, possivelmente, tempo.
$$$S$ - uma ação que depende da trajetória específica do sistema (ou seja, $$$q(t)$ )

As trajetórias reais do sistema são estacionárias, ou seja, para eles uma variação de ação$$$δS=0$ .

Se voltarmos ao exemplo com uma bola e uma parede elástica, a explicação dessa situação agora se torna muito simples. Dadas as condições de contorno que a bola deve também durante$$$t_A$ e durante $$$t_B$ chegar ao ponto $$$A$ . . , . , , . .

( ) , .