
Provavelmente tem uma pergunta razoável: por que?
Do ponto de vista pragmático, não há necessidade) Você sempre pode usar o Tungstênio condicional e, se precisar fazer isso em python, use módulos especiais que não são tão difíceis de dominar.
Mas se de repente você recebeu essa tarefa ou apenas gosta de programar, como eu, terá horas empolgantes - e às vezes não muito - de escrever e depurar um programa)
Ao escrever esta obra-prima, precisamos realmente da depuração passo a passo, então faça o download do PyCharm, VS ou de qualquer outra coisa com esse recurso. Para criar tabelas, a falta dessa função não é tão crítica, mas para criar um gráfico ...
Então, qual será o meu programa. Na entrada, serão necessários três valores: o início e o fim do segmento no qual queremos ver nossa função e o passo com o qual iremos avançar. A seguir, desenharemos uma tabela de valores de função em cada ponto do intervalo de valores especificado pelos dados de entrada. Bem, vamos desenhar o gráfico da própria função com o eixo y em movimento.
Então vamosPara começar, declararei várias funções cujos valores consideraremos. Vou especialmente bem simples
from math import sqrt def y1(x): return x**3 - 2*x**2 + 4*x - 8 def y2(x): return 1 - 1/x**2 def y3(x): return sqrt(abs(y1(x)*y2(x)))
Agora, temos três funções, duas das quais com um ponto de interrupção. No módulo matemático, que armazena todos os bolos matemáticos (incluindo co-senos, arco-tangentes e outras trigonometrias), importamos o sqrt, ou seja, a raiz quadrada. Precisamos disso para ler a função y3.
Depois disso, precisamos ler o intervalo da função por x e o passo com o qual passamos por esse intervalo. Para isso, vou usar o mapa.
Como primeiro parâmetro, essa função assume alguma função que transforma os dados de que precisamos e, como segundo argumento, algum tipo de folha de dados que precisamos processar
from_x, to_x, pace_x = map(float, input("Enter the first and the last"\ " x-coordinates and a pace dividing them by a"\ " space:").split())
Lemos os três valores inseridos em um espaço, dividimos-os em elementos por um espaço (usando o método split, que, quando chamado sem parâmetros, dividirá automaticamente a string que você especificar por espaços). Os dados inseridos usando input (), por padrão, serão do tipo str, ou seja, uma string, portanto não teremos erros aqui.
Como os números dos limites do intervalo podem ser fracionários, convertemos cada elemento da matriz resultante em um número real usando a função float.
Observe que as variáveis são declaradas sem especificar um tipo de dados. É determinado automaticamente (o tipo de dado do valor que você está tentando atribuir a uma variável) ou usando as funções str, int, float etc. definido manualmente por variáveis, aplicando essas mesmas funções aos valores. A mesma variável pode ter um tipo de dados diferente em todo o programa - basta atribuir um novo valor a ela com um tipo de dados diferente.
Por exemplo
auxiliary_variable = ""
Vamos voltar ao nosso programa. Precisamos verificar se os dados inseridos estão corretos.
O programa deve imprimir que os dados inseridos estão incorretos se:
- passo é 0
- o limite inferior do intervalo é maior que o superior e o passo é positivo (ou seja, temos uma progressão aritmética da forma xn = from_x + pace_x * (n - 1) , na qual from_x> to_x . Desde pace_x> 0, essa progressão aumentará e nós nunca chegue a_x )
- o limite inferior do intervalo é menor que o superior e o passo é negativo (raciocínio semelhante)
- os gráficos que consistem em um ponto não são informativos; portanto, o segmento no qual construímos a função deve conter pelo menos dois valores
Formulamos essas condições no código. Obviamente, o primeiro item é fácil de configurar. O segundo e o terceiro podem ser combinados em um, se você notar que o sinal da diferença entre o primeiro (de_x) e o último (to_x) deve coincidir com o sinal da etapa. Bem, o quarto ponto também não é tão complicado: o módulo da diferença entre o primeiro e o último valor não deve ser menor que o módulo step.
Por causa do módulo, podemos ter uma situação em que os sinais da diferença e da etapa não coincidam, mas a segunda condição interromperá esses casos, portanto a condição está correta.
Como resultado, essas três condições terão a seguinte aparência:
if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x):
Prosseguimos diretamente para a mesa. Para facilitar a depuração, criarei várias variáveis com nomes falados que serão responsáveis pela precisão dos números, pelo número de espaços antes do número, pelo número de espaços após o número, etc.
dials_precision = "%10.6g"
Então, o que está acontecendo aqui?

dials_precision = "%10.6g"
nesta linha, defino a precisão do número. Máximo de 10 caracteres para o número inteiro e 6 caracteres para a parte fracionária. Se tivermos um valor muito alto para esse intervalo, todos os tipos de
e-15s ou algo semelhante aparecerão.
spaces_in_the_title = int((int(dials_precision[1:3])) / 2)
dials_precision é uma string, então podemos pegar uma fatia dessa string, ou seja, algum tipo de substring. Nesse caso, precisamos obter o número 10, portanto, pegamos os caracteres nos índices 1 e 2, convertemos essa substring em um tipo de dados inteiro, dividimos por dois e arredondamos para baixo.
Precisamos dessa variável para que as inscrições no cabeçalho da tabela sejam centralizadas na célula
length_of_table_lower_bound = (int(dials_precision[1:3]) + 2) * 4 + 5
como o nome indica, essa variável é responsável pelo comprimento dos limites inferiores das células da tabela de valores da função. No total, o número ocupa 10 posições, o que significa que a coluna não pode ter largura inferior a 10. Quando obtemos números com o formato e-15 (descrito acima), o valor assume 11-12 posições. Portanto, para 10, adicionamos outro empate.
4 é responsável pelo número de colunas (x, y1, y2, y3) e 5 é pelo número de caracteres que limitam a célula em uma linha.
O restante das variáveis parece ser intuitivo, então vamos continuar imprimindo a placa
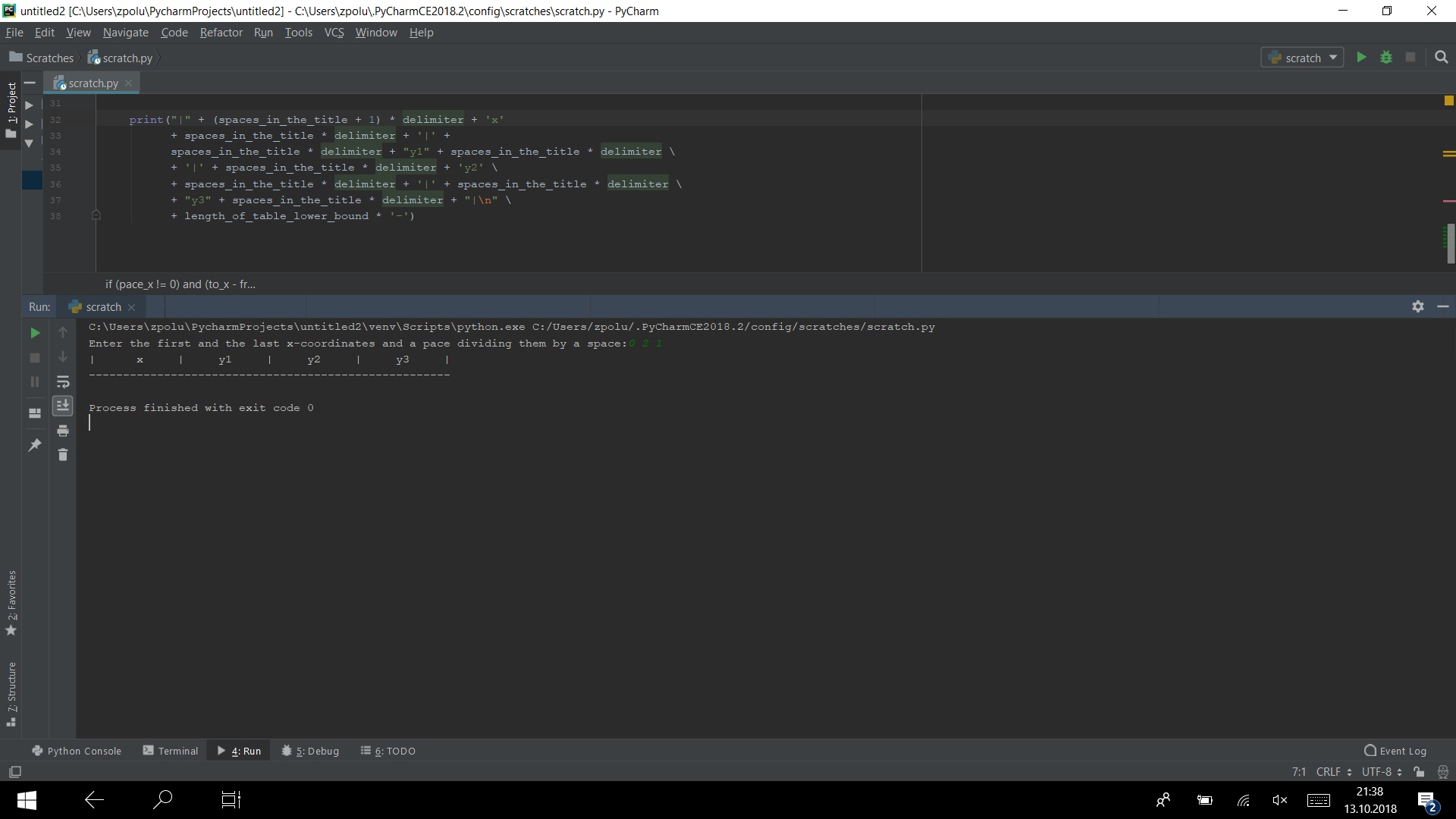
print("|" + (spaces_in_the_title + 1) * delimiter + 'x' + spaces_in_the_title * delimiter + '|' + spaces_in_the_title * delimiter + "y1" +\ spaces_in_the_title* delimiter\ + '|' + spaces_in_the_title * delimiter + 'y2'\ + spaces_in_the_title * delimiter + '|' +\ spaces_in_the_title * delimiter\ + "y3" + spaces_in_the_title * delimiter + "|\n"\ + length_of_table_lower_bound * '-')
se conectarmos todo o código que já escrevemos, no console veremos isso:
Agora precisamos imprimir os próprios valores. Para fazer isso, você precisa de um loop. Como os dados inseridos podem ser fracionários, o uso do
intervalo não funcionará, portanto, utilizarei um loop regular.
Como podemos ter uma sequência decrescente de Xs e uma sequência crescente, as condições do ciclo devem ser definidas para que essas duas opções sejam levadas em consideração. Temos uma variável criada anteriormente que armazena a resposta sobre a natureza da sequência na forma de 0 ou 1. Portanto, basta considerar dois casos e selecionar a condição apropriada para cada
while(is_sequence_decreasing and x_copy >= to_x) or\ (not is_sequence_decreasing and x_copy <= to_x):
Como para o gráfico precisamos do mínimo e do máximo do gráfico y1, que desenharemos, apresentamos variáveis especiais que serão responsáveis por min e max
y1_cur_value = y1(x_copy) min_y1_value = (min_y1_value > y1_cur_value) * y1_cur_value + \ (min_y1_value <= y1_cur_value) * min_y1_value max_y1_value = (max_y1_value < y1_cur_value) * y1_cur_value + \ (max_y1_value >= y1_cur_value) * max_y1_value negative_value_exists += y1_cur_value < 0
a construção, em essência, repete a construção de
if: ... else: ... , somente através de desigualdades booleanas.
y1_cur_value armazena o valor atual da função. Criei uma variável para não chamar constantemente uma função quando seu valor em um ponto é necessário.
Também precisaremos da presença de valores negativos para plotagem.

Agora imprima diretamente os valores. Quero que tudo seja bonito e centralizado em cada uma das células, portanto, tenho que processar manualmente cada valor para verificar o comprimento do número e selecionar o número de espaços, dependendo dele, para alinhar o valor.
Nota
Centralizar literalmente o número não funcionará. A variável responsável pela precisão possui o parâmetro g. Ele diz que um certo número de posições para números é reservado para um número (no nosso caso, 10 por padrão). Se 10 dígitos não forem discados, as posições em branco serão localizadas à esquerda das posições preenchidas. Portanto, podemos apenas centralizar uma linha de 10 posições.
aux_x = dials_precision % x_copy aux = len(aux_x) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_x) == int(dials_precision[1:3]) + 1 print('|' + delimiter * aux + aux_x + delimiter * (aux - aux_2) + '|', end='')
aux_x - uma string que já foi trazida para uma visualização com uma determinada precisão. Agora precisamos verificar o comprimento do número e selecionar o número necessário de espaços. Como não é necessário mais de um espaço de cada lado, as variáveis
bool eva são perfeitas como guardiãs do número desses mesmos espaços.
aux_2 captura o caso quando o comprimento do número é 11.
Também fazemos pelos valores de três funções
aux_y1 = dials_precision % y1_cur_value aux = len(aux_y1) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y1) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y1 + delimiter * (aux - aux_2) + '|', end='') if (x_copy != 0): aux_y2 = dials_precision % y2(x_copy) aux = len(aux_y2) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y2) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y2 + delimiter * (aux - aux_2) + '|', end='') aux_y3 = dials_precision % y3(x_copy) aux = len(aux_y3) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y3) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y3 + delimiter * (aux - aux_2) + \ "|\n" + length_of_table_lower_bound * '-') else: print((spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + '|' \ + (spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + "|\n" \ + length_of_table_lower_bound * '-') x_copy += pace_x
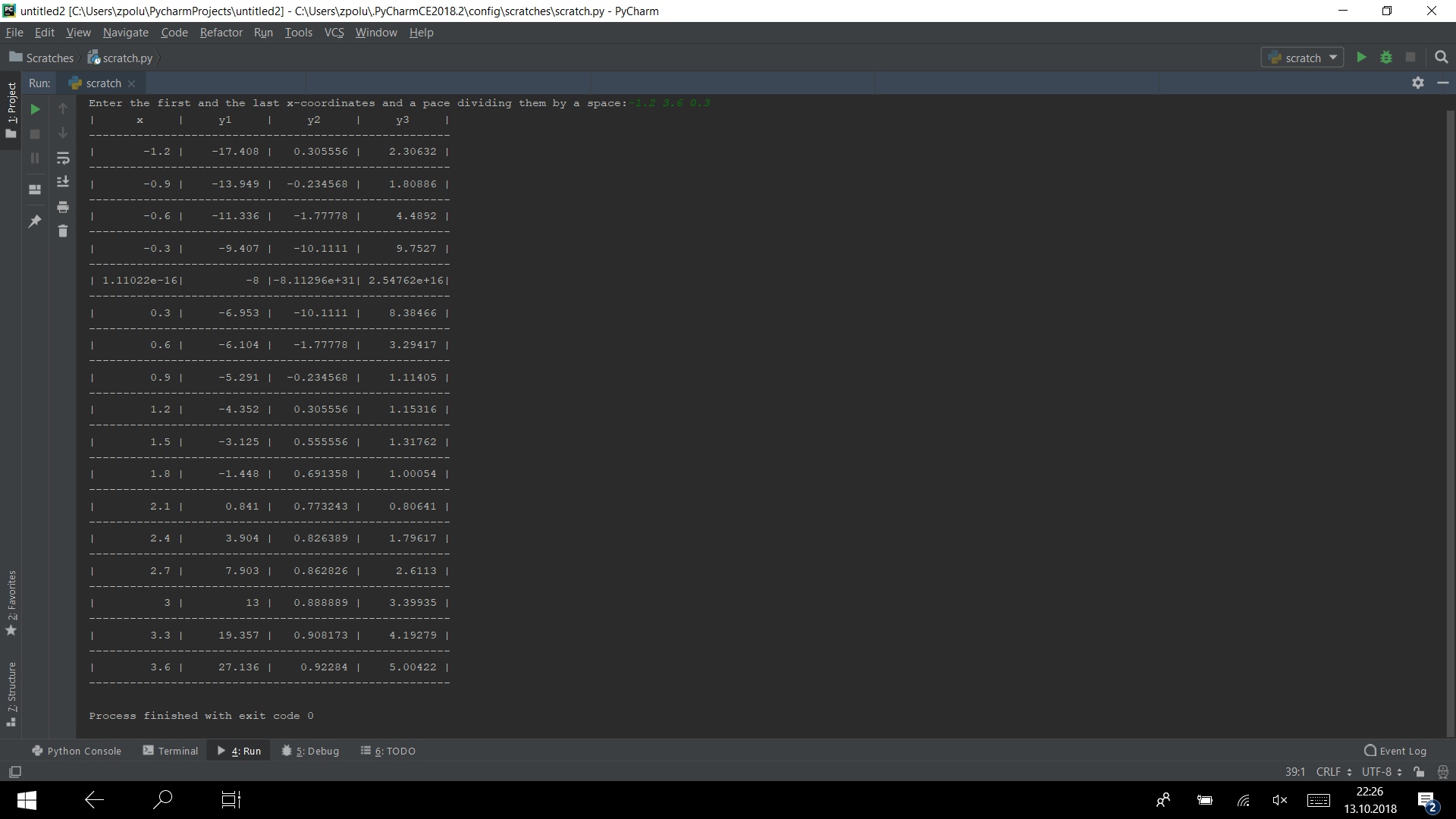
Como eu disse no começo, a segunda e a terceira funções têm pontos de interrupção - ambas as funções não existem no ponto x = 0. Portanto, também precisamos capturar esses casos.
Bem, não esqueça de aumentar o valor x atual para que não tenhamos um ciclo interminável.
Vamos coletar todo o código em um programa e executá-lo, por exemplo, no teste -1,2 3,6 0,3
from math import sqrt def y1(x): return x**3 - 2*x**2 + 4*x - 8 def y2(x): return 1 - 1/x**2 def y3(x): return sqrt(abs(y1(x)*y2(x))) from_x, to_x, pace_x = map(float, input("Enter the first and the last"\ " x-coordinates and a pace dividing them by a"\ " space:").split()) if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x): dials_precision = "%10.6g"
Na segunda parte desta criação, criaremos gráficos
 Para continuar ...
Para continuar ...