
Continuamos familiarizados com a muito jovem, mas incrivelmente bela e poderosa linguagem de programação Julia . A versão beta de seis anos finalmente terminou, então agora você não pode ter medo de alterações de sintaxe. E enquanto todos estão discutindo se é bom ou ruim começar a indexar a partir de uma, a comunidade agitada está brincando: novas bibliotecas estão surgindo, novas bibliotecas estão sendo atualizadas, projetos sérios estão sendo iniciados e os alunos estão ensinando ativamente esse idioma nas universidades. Então não vamos ficar para trás! Tornamos o chá mais forte, porque codificaremos esta noite!
Preparação para o trabalho
Aqui há uma pequena revisão em russo, também no hub, há um conhecimento do idioma e das instruções de instalação . Novamente, concentrando-se na necessidade do Windows Management Framework , haverá problemas com o download de pacotes.
Após a atualização, o JuliaPRO agora inclui apenas o Juno . Mas eu pessoalmente gosto mais do Jupyter : não houve problemas com ele no laptop, além de ser conveniente trabalhar no navegador e criar imediatamente notas e fórmulas, em geral, ideais para criar relatórios, slides ou manuais.
Casar com Jupyter e Julia 1.0.1 Existem vários pacotes para Julia, os mais bem-sucedidos estão incluídos nos lotes como back-end. Plots.jl - metalinguagem de Plots.jl : isto é, uma interface para várias bibliotecas de gráficos. Assim, o Plots.jl , Plots.jl verdade, apenas interpreta seus comandos e cria gráficos usando algum tipo de biblioteca de gráficos. Essas bibliotecas de gráficos de plano de fundo são chamadas de back-end. A melhor parte é que você pode usar muitas bibliotecas gráficas diferentes com a sintaxe Plots.jl , e também veremos que o Plots.jl adiciona novos recursos a cada uma dessas bibliotecas!
Instale pacotes gráficosPara instalar pacotes, execute os comandos no REPL, Juno ou Jupyter:
# Pkg.add("Plots") # 0.7.0 julia>] pkg>add Plots pkg>add GR pkg>add PyPlot pkg>add Gadfly pkg>add PlotlyJS pkg>add UnicodePlots
Não é necessário instalar todos os pacotes, mas você deve saber que cada um deles tem suas próprias características . Eu prefiro plotlyjs () : embora não seja diferente na velocidade, é muito interativo. Há um zoom, movendo-se ao longo do plano, além da capacidade de salvar o arquivo e, se você salvar o documento Jupyter como html, todos os recursos serão salvos. Assim, você pode adicionar ao site ou fazer uma apresentação interativa. Mais informações nas páginas: Terrenos , Gadfly
Padrão primário sem fim
Implementou a ideia de um artigo sobre Habr . Em poucas palavras: e se pegarmos a coordenada do ponto e usarmos uma operação, digamos, XOR ou AND bit a bit E entre a abscissa e a ordenada, e depois verificar o número por simplicidade ou por pertencer aos números de Fibonacci e, se a resposta for sim, preencha o ponto com uma cor, e com um negativo em outro? Verifique:
Para operação% using Plots plotlyjs() function eratosphen(n, lst) # ar = [i for i=1:n] ar[1] = 0 for i = 1:n if ar[i] != 0 push!(lst, ar[i]) for j = i:i:n ar[j] = 0 end end end end ertsfn = [] eratosphen(1000, ertsfn) # print(ertsfn) # print( size(ertsfn) ) # -> 168 N = 80 M = 80 W1 = [in( x % y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x % y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y is prime?") p2 = spy(W2, title = "x % y") plot(p1, p2, layout=(2),legend=false)
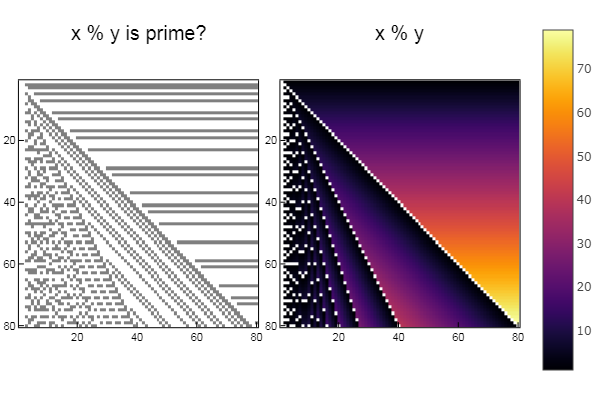
Para operação + W1 = [in( x + y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x + y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x + y is prime?") p2 = spy(W2, title = "x + y") plot(p1, p2, layout=(2),legend=false)
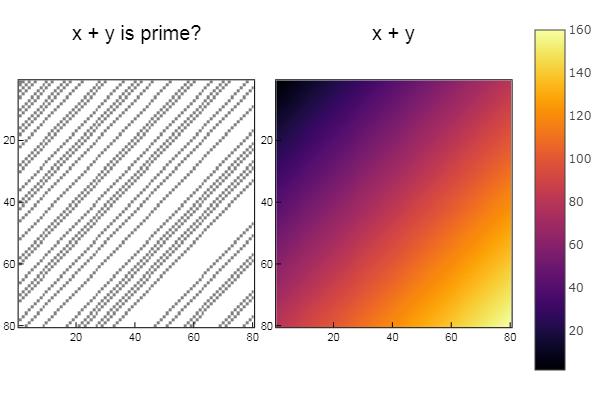
Para operação | W1 = [in( x | y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x | y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x | y is prime?") p2 = spy(W2, title = "x | y") plot(p1, p2, layout=(2),legend=false)

Para operação e W1 = [in( x & y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x & y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x & y is prime?") p2 = spy(W2, title = "x & y") plot(p1, p2, layout=(2),legend=false)
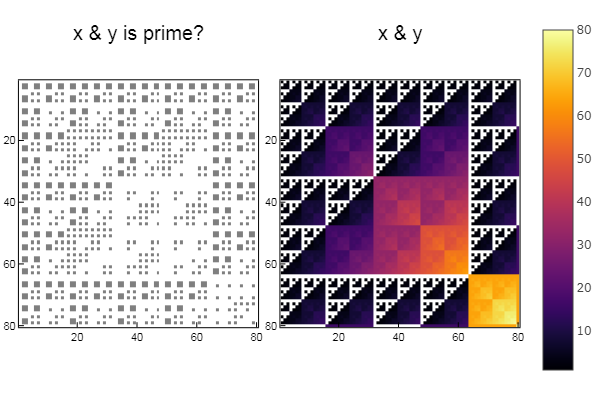
Para operação xor W1 = [in( xor(x, y), ertsfn) for x = 1:N, y = 1:M]; W2 = [xor(x, y) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y is prime?") p2 = spy(W2, title = "x xor y") plot(p1, p2, layout=(2),legend=false)
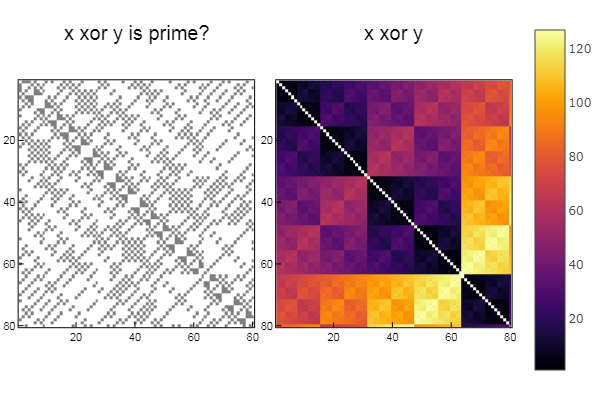
E agora tudo é o mesmo, mas para os números de FibonacciVocê pode fazer uma série como de costume com algo como:
function fib(n) a = 0 b = 1 for i = 1:n a, b = b, a + b end return a end fbncc = fib.( [i for i=1:10] )
Mas vamos usar a representação matricial (em mais detalhes ):
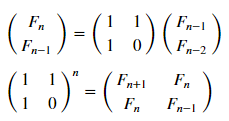
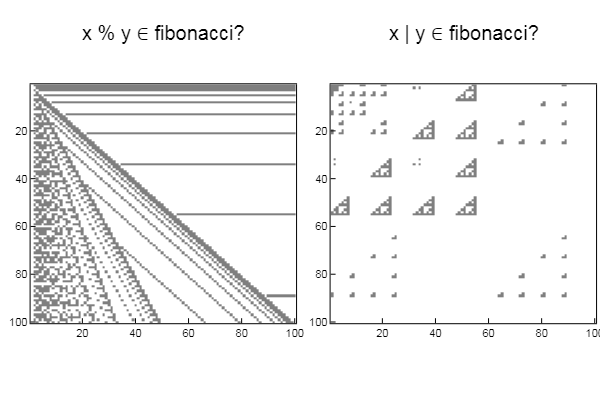
matr_fib = n -> [1 1; 1 0]^(n-1) # , n-1 mfbnc = [ matr_fib( i )[1,1] for i=1:17]; # 1,1 n- N = 100 M = N W1 = [in( x % y, mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x | y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y ∈ fibonacci?") p2 = spy(W2, title = "x | y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
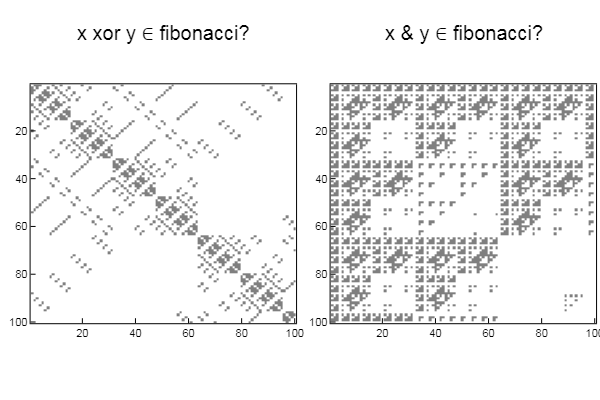
W1 = [in( xor(x, y), mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x & y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y ∈ fibonacci?") p2 = spy(W2, title = "x & y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
Reflexão de uma figura relativamente reta
Este tipo de exibição é determinado pela matriz:
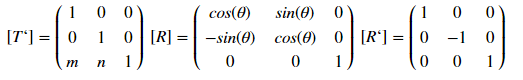
onde [T '], [R] e [R'], respectivamente, as matrizes de deslocamento, rotação e reflexão. Como isso funciona? Vamos analisar um exemplo de deslocamento - para um ponto com coordenadas (x, y), o deslocamento por m por x e por n pelo jogo será determinado pela transformação:
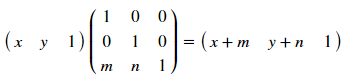
Essas matrizes permitem transformações para vários polígonos. O principal é gravar coordenadas umas nas outras e não esquecer a coluna da unidade no final. Assim [T]:
- muda a linha na origem junto com o polígono sendo transformado
- gira para coincidir com o eixo X
- reflete todos os pontos do polígono em relação a X
- seguido de rotação e transferência reversa
O tópico é descrito em mais detalhes no livro Rogers D., Adams J. Fundamentos Matemáticos da Computação Gráfica
Agora codifique-o!
using Plots plotlyjs() f = x -> 0.4x + 2 # # X = [2 4 2 2]' Y = [4 6 6 4]' xs = [-2; 7] # ys = f(xs) inptmtrx = [ XY ones( size(X, 1), 1 ) ] # m = 0 n = -f(0) # Y displacement = [1 0 0; 0 1 0; mn 1] a = (ys[2]-ys[1]) / (xs[2]-xs[1]) # θ = -atan(a) rotation = [cos(θ) sin(θ) 0; -sin(θ) cos(θ) 0; 0 0 1] reflection = [1 0 0; 0 -1 0; 0 0 1] T = displacement * rotation * reflection * rotation^(-1) * displacement^(-1) # outptmtrx = inptmtrx * T plot( X, Y) plot!( xs, ys ) plot!( outptmtrx[:,1], outptmtrx[:,2] )
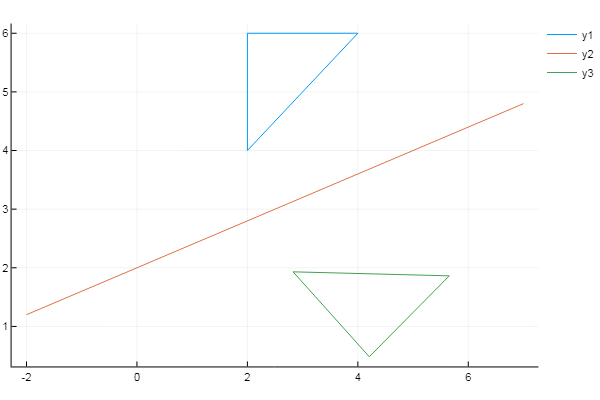
Fato interessante: se você se livrar dos caracteres gregos e substituir a primeira linha por
function y=f(x,t) y=0.4*x + 2 endfunction,
Como os colchetes [] enquadram os índices das matrizes em () e as jangadas no plot( X, Y, xs, ys, trianglenew(:,1), trianglenew(:,2) ) , esse código é executado no Scilab .
Trabalhar com gráficos tridimensionais
Alguns desses pacotes suportam a construção de gráficos tridimensionais. Mas também gostaria de mencionar a ferramenta de visualização bastante poderosa do Makie , que funciona em conjunto com os pacotes GLFW e GLAbstraction que implementam o OpenGL em julho. Mais informações sobre Makie . Escondemos sua aprovação sob
spoiler using Makie N = 51 x = linspace(-2, 2, N) y = x z = (-x .* exp.(-x .^ 2 .- (y') .^ 2)) .* 4 scene = wireframe(x, y, z) xm, ym, zm = minimum(scene.limits[]) scene = surface!(scene, x, y, z) contour!(scene, x, y, z, levels = 15, linewidth = 2, transformation = (:xy, zm)) scene
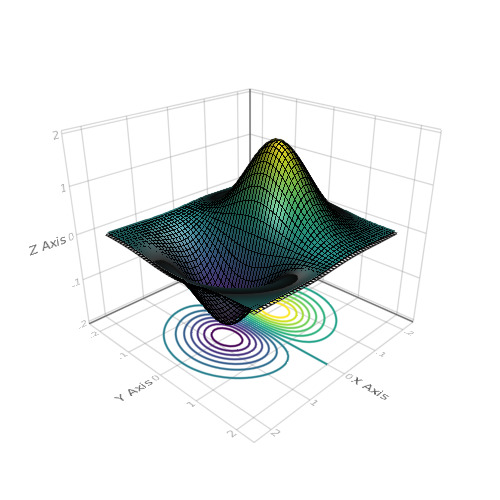
wireframe(Makie.loadasset("cat.obj"))

using FileIO scene = Scene(resolution = (500, 500)) catmesh = FileIO.load(Makie.assetpath("cat.obj"), GLNormalUVMesh) mesh(catmesh, color = Makie.loadasset("diffusemap.tga"))

x = Makie.loadasset("cat.obj") mesh(x, color = :black) pos = map(x.vertices, x.normals) do p, n p => p .+ (normalize(n) .* 0.05f0) end linesegments!(pos, color = :blue)
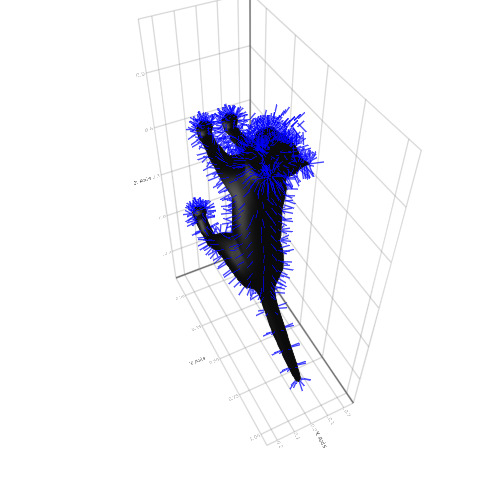
Isso é tudo com os gráficos. Interatividade, animação, 3d, big data ou construção rápida de gráficos simples - os pacotes em constante evolução satisfarão quase todos os gostos e necessidades; além disso, tudo é muito fácil de aprender. Sinta-se livre para baixar exercícios práticos e continuar a compreender Julia!
UPD: Todas as listagens acima são feitas em Jupyter com julia 0.6.4. Infelizmente, algumas funções do meta-pacote Plots foram removidas ou renomeadas, por isso continuamos monitorando as atualizações, mas por enquanto o espião é completamente substituído:
julia> using GR julia> Z = [x | y for x = 1:40, y = 1:40]; julia> heatmap(Z)