Início iniciado
Da última vez, decidi construir uma tabela de valores de funções. Chegou a hora de prosseguir com a construção do próprio cronograma, para o qual tudo isso começou.
Portanto, a ideia principal é a seguinte. Gire o eixo de coordenadas 90 graus no sentido horário. Isso é necessário para simplificar a construção sem armazenar dados sobre cada ponto em qualquer planilha.
Em seguida, limitamos o eixo de coordenadas do jogo a 82 caracteres para melhor legibilidade do gráfico. É claro que, ao fazer isso, perdemos a precisão e o cronograma será mais esquemático (muito apertado), especialmente para funções "legais", mas ainda assim.
Depois disso, calculamos a posição do eixo x em relação ao eixo dos jogadores, ou seja, procuramos em que lugar teremos um ponto (x, 0). Bem, então atribuiremos linha por linha x o valor da função y1 neste momento.
Vamos lá
Primeiro, precisamos da seguinte fórmula:

Atribuiremos 80 posições ao próprio horário, os dois lugares restantes serão puramente decorativos. Com essa fórmula, descobrimos qual intervalo de valores corresponde a uma posição em nosso gráfico. Então podemos marcar corretamente o ponto atual nele.
As principais idéias são descritas, então vamos para o próprio código
dial_length = 12 label = " y1 = x**3 - 2*x**2 + 4*x - 8" print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 82, 'y' , 82*'-']));
Inclusive graças aos comentários da primeira parte, aprendi sobre o
formato . Pareceu-me realmente mais conveniente do que minhas danças com um pandeiro, de modo que um enorme código de cálculo de travessões se transformou em duas linhas
print("{1:>{0}}".format(len(label) + dial_length, label), '\n')
A unidade é responsável pelo número do elemento passado como argumento para a função format, ou seja, é um "link" (não literalmente) para a variável label, que realmente exibimos na tela. A numeração é exatamente igual à das folhas - a partir do zero.
Um par de caracteres
:> é usado para alinhar o texto exibido no lado direito. Bem,
{0} após o caractere
> ser necessário para determinar o número de posições de linha necessárias.
Ou seja, neste caso, reservamos as posições len (label) + dial_length da etiqueta de linha, e a própria etiqueta ocupa apenas len (label), e alinhamos o texto no lado direito dentro do conjunto dessas posições.
print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print(dial_length*' ' + label, '\n')
essas linhas são equivalentes
Sim, para seqüências de caracteres, provavelmente é mais fácil usar a segunda opção, mas aplicar a primeira para desenvolvimento geral não será prejudicial)
print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 82, 'y' , 82*'-']));
Mesmo matrizes do tipo r_value (em C ++) podem ser amontoadas no formato, isto é, criadas diretamente ao passar um argumento.
Fixamos as variáveis que são constantes conosco, ou seja, elas não dependem do valor atual da função.
No python, não há uma
constante condicional para designar constantes, portanto, é habitual chamar essas variáveis em letras maiúsculas e simplesmente não alterá-las.
MAX_Y1_VALUE_DIFFERENCE = (max_y1_value - min_y1_value) + \ (max_y1_value == min_y1_value) RATIO = MAX_Y1_VALUE_DIFFERENCE / 80 AXIS_X_POS = abs(int((- min_y1_value) / RATIO)) if (AXIS_X_POS > 80): AXIS_X_POS = 81
Como RATIO, por razões óbvias, não pode ser igual a 0, MAX_Y1_VALUE_DIFFERENCE deve ser um número positivo. É por isso que o segundo mandato está no lado direito da tarefa.
A posição do eixo x calculada pela fórmula
De onde vem essa fórmula? Simplesmente calculamos a proporção dos segmentos (no eixo do jogo) desde o início do eixo (min (y1)) até o valor atual da função (y1 (x)) e o segmento desde o início do eixo até o final (max (y1)). Bem, multiplicamos essa relação por 80 para encontrar a distância do início do eixo ao valor atual em espaços (portanto, você pode usar apenas números inteiros), o que refletirá a fórmula da relação no gráfico.
Como estamos interessados na posição em y1 (x) = 0, substituímos os valores necessários e voilá na fórmula.
Agora você pode ir diretamente para os valores de impressão
while (is_sequence_decreasing and from_x >= to_x) or \ (not is_sequence_decreasing and from_x <= to_x): y1_cur_value = y1(from_x) cur_y1_value_and_min_difference = (y1_cur_value - min_y1_value) + \ (y1_cur_value == min_y1_value) * \ ((max_y1_value == min_y1_value)) pos_of_y = int(cur_y1_value_and_min_difference * 80 / \ MAX_Y1_VALUE_DIFFERENCE)
O ciclo já é familiar para nós. Teremos que contar cada valor da função uma segunda vez, para não armazená-los em uma planilha ou em outra coisa.
A posição do jogo é calculada pela fórmula acima.
Teremos que corrigir a diferença superior da fórmula, prevendo o caso em que, na fórmula, obtemos a incerteza da forma zero por zero. Se surgir tal incerteza, isso significa que o valor atual é y1 (x) = max (y1), o que significa que o valor atual do jogo coincidirá com o final do eixo y.
print("{1:^{0}.6g}".format(dial_length, from_x), end='') if (negative_value_exists): if y1_cur_value <= 0 - RATIO / 2: req_aux = AXIS_X_POS - pos_of_y if (req_aux != 0): print(pos_of_y * ' ' + '*' + (req_aux - 1) * ' ' + '|') else: print((AXIS_X_POS - 1) * ' ' + '*' + '|') elif y1_cur_value >= 0 + RATIO / 2: req_aux = pos_of_y - AXIS_X_POS if (req_aux != 0): print(AXIS_X_POS * ' ' + '|' + (req_aux - 1) * ' ' + '*') else: print((AXIS_X_POS) * ' ' + '|*') else: print(AXIS_X_POS * ' ' + '*') else: print('|' + pos_of_y* ' ' + '*') AXIS_X_POS = 0 from_x += pace_x print((dial_length + AXIS_X_POS) * ' ' + '|\n', (dial_length + AXIS_X_POS - 3) * ' ' + 'x V')
Esta parte do código é diretamente responsável pela impressão do próprio gráfico.
print("{1:^{0}.6g}".format(dial_length, from_x), end='')
Aqui, o formato foi muito útil e simplificou o código.
^ nos permite alinhar o número no centro da área selecionada (neste caso, 12 posições).
g é responsável pelos números - se eles não tiverem uma parte fracionária, ela não será impressa (número como int), caso contrário - 6 casas decimais
Como nosso gráfico é limitado a um espaço de 80 caracteres ao longo do eixo y, em nosso gráfico o valor da função no ponto coincidirá com o eixo x não apenas no caso y1 (x) = 0, mas também na vizinhança [0 - RATIO / 2, 0 + RATIO / 2]
No total, temos três casos da localização do asterisco (isto é, o ponto) e o manche vertical (ou seja, o eixo x): '* |' (y1 (x) <= 0 - RATIO / 2), '*' (0 - RATIO / 2 <y1 (x) <0 + RATIO / 2), '| *' (y1 (x)> = 0 + RATIO / 2), consideraremos esses três casos.
- y1 (x) <= 0 - RELAÇÃO / 2
Nesse caso, o ponto está localizado no eixo x, portanto, estamos procurando a distância do ponto ao eixo em espaços. Devido ao arredondamento dos números, pode acontecer que os valores das variáveis AXIS_X_POS e pos_of_y possam coincidir. Mas isso não pode ser, pois neste caso estaríamos no terceiro caso. No nosso caso, o ponto não coincide com o eixo x, portanto, é necessária uma condição adicional, que reduzirá em 1 a variável pos_of_y em caso de igualdade. - y (x)> = 0 + RELAÇÃO / 2
O caso é idêntico ao primeiro caso, apenas o ponto estará localizado no outro lado do eixo x e todas as ações acima serão ajustadas para esse - o resto
O caso mais simples - basta imprimir um asterisco no lugar do eixo
Ou seja, se tivermos valores negativos (y1 (x) <0). Caso contrário, basta digitar '|' e determine a posição do ponto.
Bem, finalizamos o programa com um eixo x adicional.
Então, o código que acabou:
dial_length = 12 label = " y1 = x**3 - 2*x**2 + 4*x - 8" print("{1:^{0}.6f}".format(dial_length, x_copy)) print("{1:>{0}}".format(len(label) + dial_length, label), '\n') print("{aux[1]:>{aux[0]}}\n {aux[2]:>{aux[0]}}>\n".format(aux = [dial_length + 81, 'y' , 82*'-']), end=''); MAX_Y1_VALUE_DIFFERENCE = (max_y1_value - min_y1_value) + \ (max_y1_value == min_y1_value) RATIO = MAX_Y1_VALUE_DIFFERENCE / 80 AXIS_X_POS = abs(int((- min_y1_value) / RATIO)) if (AXIS_X_POS > 80): AXIS_X_POS = 81 while (is_sequence_decreasing and from_x >= to_x) or \ (not is_sequence_decreasing and from_x <= to_x): y1_cur_value = y1(from_x) cur_y1_value_and_min_difference = (y1_cur_value - min_y1_value) + \ (y1_cur_value == min_y1_value) * \ ((max_y1_value == min_y1_value)) pos_of_y = int(cur_y1_value_and_min_difference * 80 / \ MAX_Y1_VALUE_DIFFERENCE) print("{1:^{0}.6g}".format(dial_length, from_x), end='') if (negative_value_exists): if y1_cur_value <= 0 - RATIO / 2: req_aux = AXIS_X_POS - pos_of_y if (req_aux != 0): print(pos_of_y * ' ' + '*' + (req_aux - 1) * ' ' + '|') else: print((AXIS_X_POS - 1) * ' ' + '*' + '|') elif y1_cur_value >= 0 + RATIO / 2: req_aux = pos_of_y - AXIS_X_POS if (req_aux != 0): print(AXIS_X_POS * ' ' + '|' + (req_aux - 1) * ' ' + '*') else: print((AXIS_X_POS) * ' ' + '|*') else: print(AXIS_X_POS * ' ' + '*') else: print('|' + pos_of_y* ' ' + '*') AXIS_X_POS = 0 from_x += pace_x print((dial_length + AXIS_X_POS) * ' ' + '|\n', (dial_length + AXIS_X_POS - 3) * ' ' + 'x V')
Execute o programa em vários testes
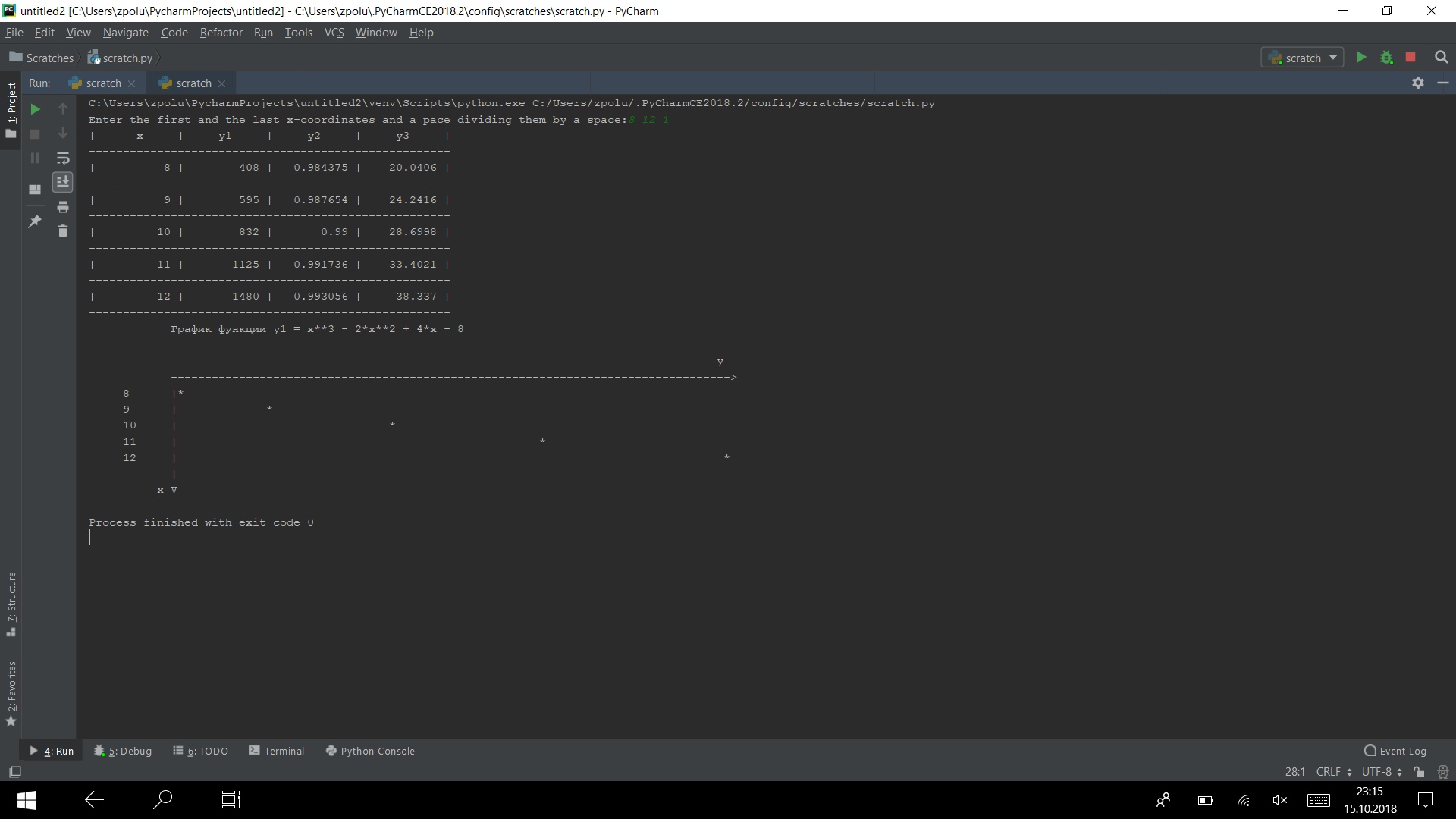
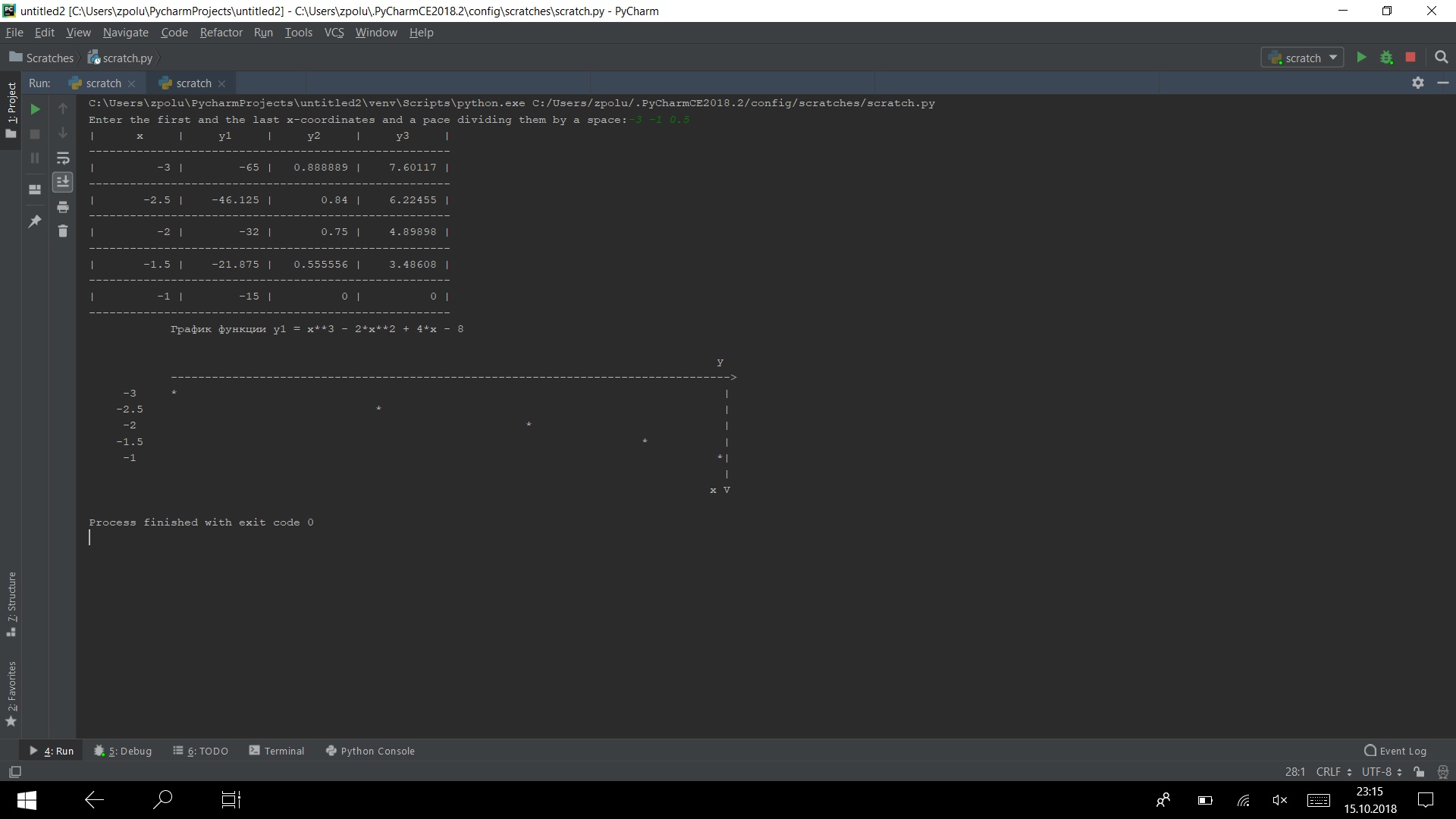
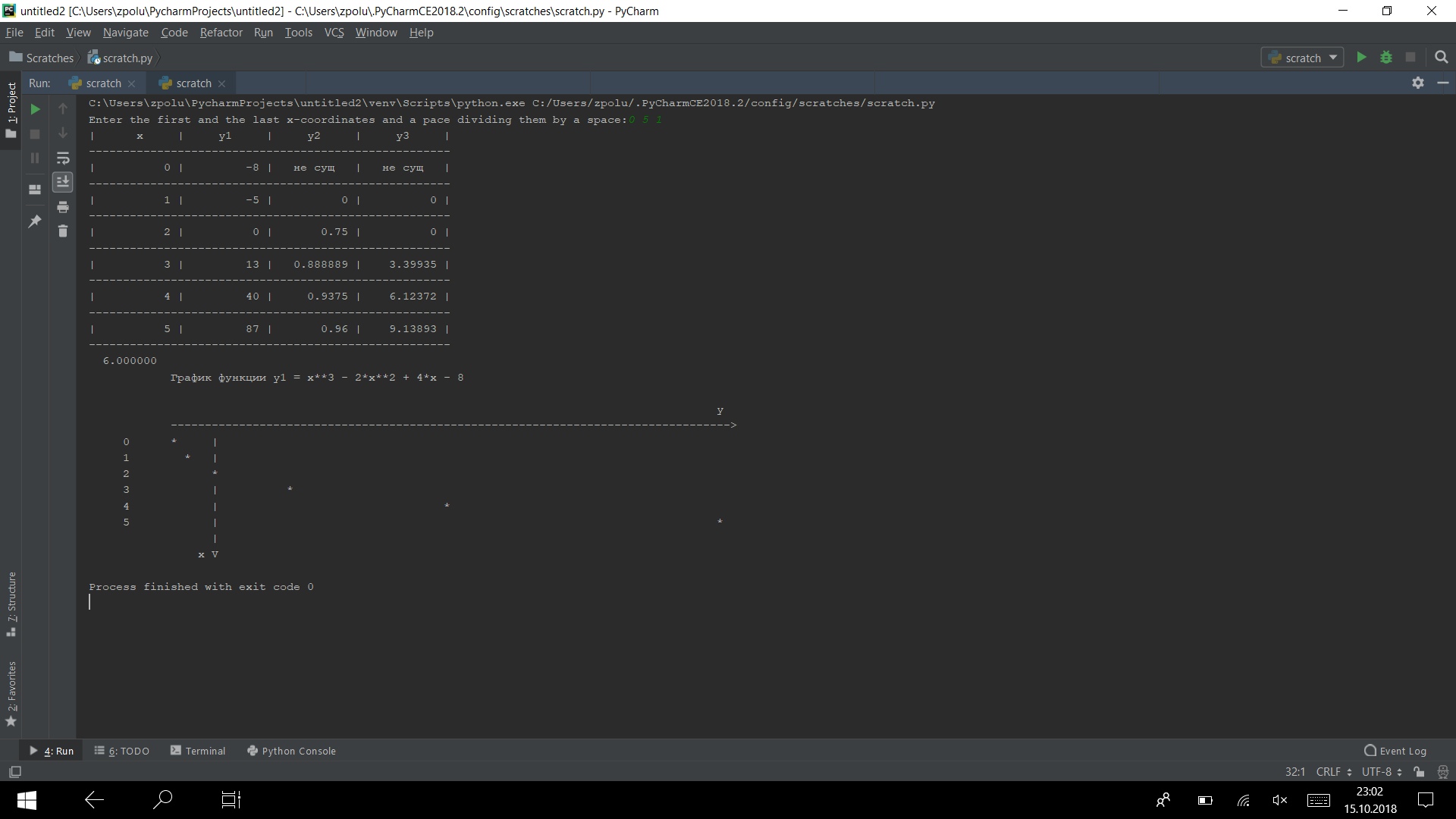
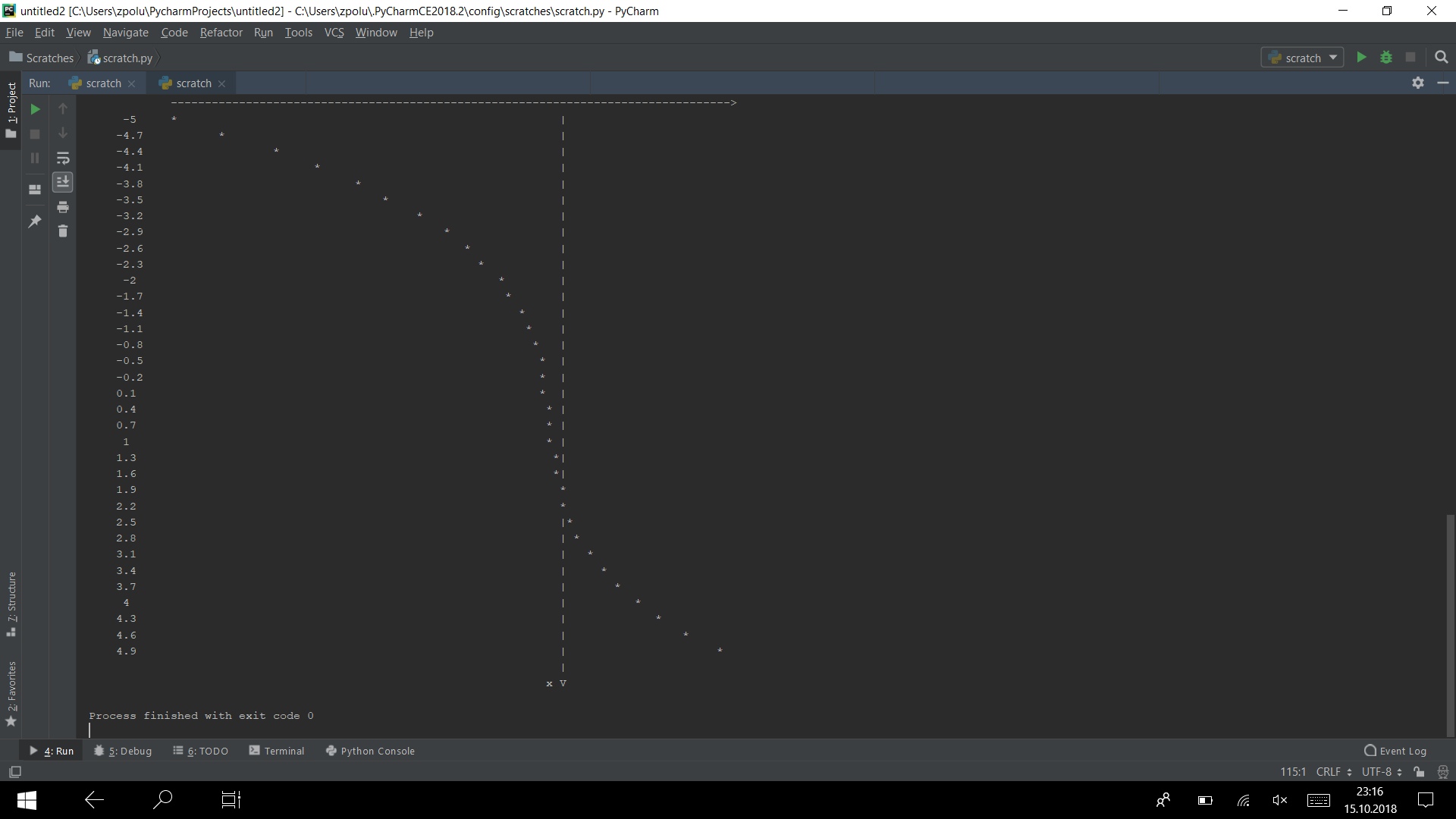
Funciona)
